Prediction of remaining service life of train control center based on hyper-ellipsoidal Markov
-
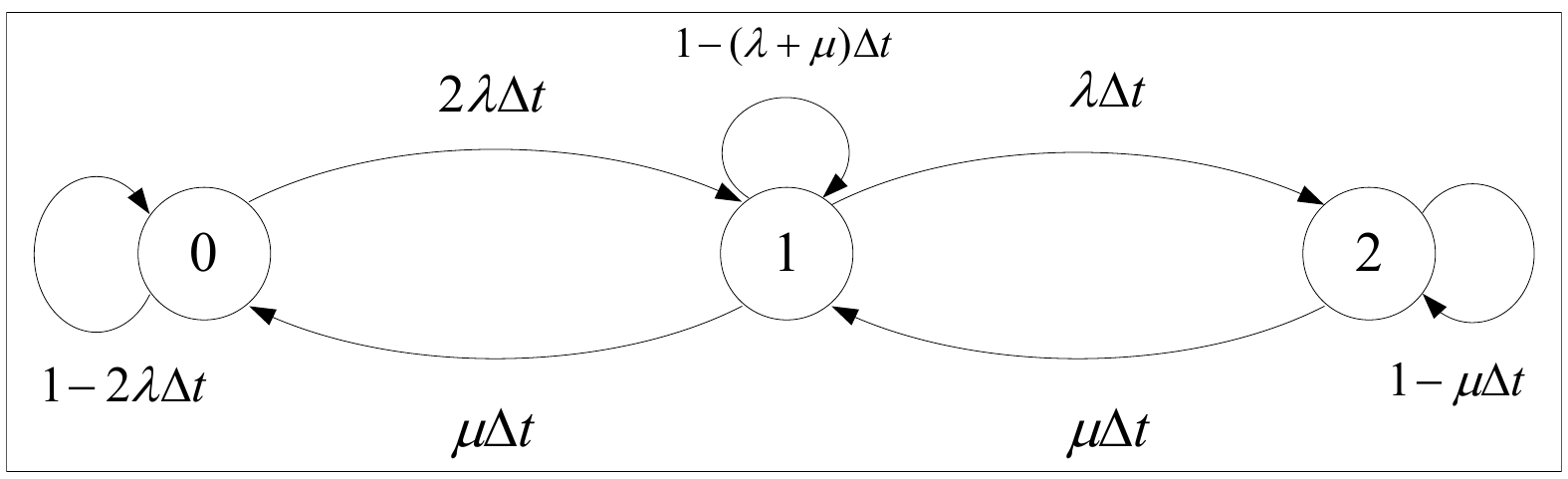
摘要: 为研究设备可用度对列车控制中心（TCC，Train Control Center）的影响和预测TCC的剩余使用寿命（RUL ，Remaining Useful Life），降低TCC的故障发生率，确保车辆安全运行，构建TCC动态故障树模型。通过引入Markov理论，将其转化为Markov模型，设计了TCC可用度评估与RUL预测方法；考虑了TCC的失效率和共因失效，利用D-S（Dempster-Shafer）证据理论对失效数据作数据融合处理，得到TCC设备初始故障区间概率；在此基础上，采用超椭球模型约束设备初始故障区间概率，得到更加精确的底事件故障区间概率；画出Markov状态转移图，用矩阵推导出TCC可用度和RUL的函数关系式，且对可用度的计算还考虑了维修因素。以兰州—乌鲁木齐客运专线某TCC数据作为分析案例，用该方法计算TCC及其各设备的可用度，并预测TCC的RUL。结果表明：与通用方法相比，评估结果相同，但评估信息更丰富。Abstract: To study the impact of equipment availability on Train Control Center (TCC) and predict the Remaining Useful Life (RUL) of TCC, reduce the occurrence rate of TCC failures, and ensure safe vehicle operation, this paper constructed a TCC dynamic fault tree model. By introducing Markov theory and transforming it into a Markov model, the paper designed a TCC availability evaluation and RUL prediction method, considered the failure rate and common cause failure of TCC, used the D-S (Dempster Shafer) evidence theory to fuse the failure data and obtain the initial failure interval probability of TCC equipment. On this basis, the paper used a hyper-ellipsoid model to constrain the initial failure interval probability of the equipment and obtain a more accurate probability of the bottom event failure interval, drew a Markov state transition diagram, derived the functional relationship between TCC availability and RUL using a matrix, and also considered maintenance factors while calculating availability. The paper took the data of a certain TCC on the Lanzhou-Urumqi passenger dedicated line as an analysis case, used this method to calculate the availability of TCC and its various equipment, and predicted the RUL of TCC. The results show that compared with general methods, this method has the same evaluation results, but richer evaluation information.
-
随着人工智能和物联网技术的不断发展，作为一种智能硬件，服务机器人产品将通过与软件加深融合的方式对传统设备进行智能化改造，不断实现更为强大的功能和更为广泛的应用场景。作为物联网生态系统中的信息交换中枢，服务机器人还将借助互联网和云技术为其他联网设备提供随时、随地的信息输入，并通过人工智能技术进一步代替用户对其他联网设备进行自主操控，为用户提供智能化服务[1]。
北京—张家口高速铁路（简称：京张高铁）是目前我国数字化、信息化、智能化水平较高的铁路，也是服务2022年北京冬奥会和冬残奥会（简称：冬奥会）的重要交通基础设施之一，将为北京、延庆、张家口3地赛区提供高品质、高安全性、高科技含量的冬奥会交通服务[2]，满足多国运动员、媒体、观众等在冬奥会期间的出行需求。本文通过模块集成、软件融合，将服务机器人与铁路既有数据相结合，以实现更为强大的服务功能，拓展应用场景[3]。
1 多功能旅客服务机器人概述
多功能旅客服务机器人包含人机交互系统和移动底盘，同时搭载人脸识别摄像机、身份证核验模块和二维码扫描模块。人机交互系统通过铁路外部服务网与机器人后台管理系统进行数据交互及联动，实现问询、语音交互、站内导航、迎宾导引等人机交互及展示[4]；移动底盘结合激光避障、超声波、3D摄像头、碰撞传感器等多传感器模块，实现机器人的移动、避障、自主回充及调配多机器人交通策略，通过结合物联闸机、爱心通道，可远程控制闸机开关、直梯呼叫，实现旅客无感进站，减少旅客操作及物体接触；多功能旅客服务机器人搭载人脸识别摄像机，接入铁路视频监控系统，可通过后台控制提供移动视频监视服务，同时结合身份证核验模块、二维码扫描模块，通过前端采集用户身份信息，与后台管理系统比对，实现人脸核验、进站验票的功能，架构如图1所示。
2 多功能旅客服务机器人功能
多功能旅客服务机器人功能架构，如图2所示。
2.1 资讯服务
旅客可通过多功能旅客服务机器人获取铁路相关资讯及公共资讯。多功能旅客服务机器人能够帮助旅客查询铁路时刻表、票务信息、开停检信息、站内设施信息、天气信息、冬奥赛事信息、周边地标等，通过预先配置的交互流程和知识库向旅客展示及交互。旅客可通过终端人机交互界面、语音交互或自定义讲解的方式获取各种资讯服务。
2.2 语音问询服务
多功能旅客服务机器人处于待机状态时，旅客可通过人脸识别、触摸屏幕和语音唤醒3种方式对机器人进行唤醒。当多功能旅客服务机器人被唤醒时，通过扬声器阵列、头部跟踪、视觉跟踪技术定位旅客，转向唤醒方向，播报欢迎语，并且针对VIP旅客提供个性化欢迎语及打招呼方式[5]。语音交互过程中，多功能旅客服务机器人通过语音播报、屏幕演示的方式对旅客问题作出答复，当遇到无法识别的语句时，播报“兜底金句”并引导旅客使用屏幕菜单触摸交互方式解决问题。技能问答可选择触发机器人讲解、引领任务，帮助解决旅客问询，拓宽旅客资讯服务获取渠道。
2.3 站内导航服务
旅客可通过多功能旅客服务机器人获取车站站内设施信息及候车引导信息，选择相应导航点位获取导航路线，通过预先配置的交互流程向旅客展示及交互，并通过物联爱心通道、闸机的方式，带领旅客通过人脸核验，乘坐直梯到达指定点位。
2.4 迎宾导引服务
多功能旅客服务机器人在进站高峰时段前往进站口迎宾待机，旅客唤醒机器人后可通过人脸识别、刷身份证/护照的方式获取已购买车票的车次、开停检、检票口信息。机器人识别对象为需要帮助的老年人时，可选择触发机器人引导任务，由机器人引导旅客至相应设施点或检票口。
2.5 开停检信息提醒服务
铁路系统信息对接平台获取车站各车次信息、检票口信息、发车时间信息及开停检信息，在相应车次检票前10 min，多功能旅客服务机器人自动到达指定检票口指定区域进行巡游，播报相应车次检票提醒信息。当旅客与机器人交互时，通过扫描交互的旅客，采集人脸信息，获取旅客相应车次信息、检票口信息、发车时间信息及开停检信息并告知旅客。
2.6 移动验检票服务
在相应车次检票前2 min，多功能旅客服务机器人自动到达指定检票口，切换至检票模式。旅客可通过身份证、护照或二维码扫码验证，多功能旅客服务机器人同时抓拍旅客人脸信息并上传后台记录，推送至铁路系统信息对接平台，与票务系统信息进行比对，验证成功屏幕显示绿色通过标识，失败显示红色拒绝通过标识并进行声音报警。多功能旅客服务机器人有助于解决检票拥堵问题，降低旅客误车率。
2.7 移动视频监控服务
多功能旅客服务机器人配备接入视频监控系统摄像机，将视频图像通过5G专网实时上传铁路视频监视后台，支持后台人员操控机器人到监控死角查看。
2.8 疫情防控服务
多功能旅客服务机器人可定时播报疫情防控信息、安全宣传信息，对接铁路站内热力电子地图，当发现人员聚集情况时，前往相应区域播报防疫信息。
3 关键技术
3.1 基于环境自然导航的SLAM激光导航技术
针对高铁站现场环境复杂、人员流动大、设备设施多的情况，为解决机器人在未知环境运动时的定位与地图构建问题，多功能旅客服务机器人采用基于环境自然导航的同步定位（SLAM，Simultaneous Localization And Mapping）与建图激光导航技术，以最开始放置的位置为起点，自主扫图，结合编码器计算运动里程信息，通过自身所携带的内部传感器和外部激光传感器对自身进行定位，同时通过获取的环境信息构建现场地图；通过机器人装载的激光传感器获取的激光数据，结合观测模型对机器人位姿进行精确修正，得到机器人的精确定位；在精确定位的基础上，将激光数据添加到栅格地图中。如此反复，多功能旅客服务机器人在环境中运动，最终完成整个场景地图的构建[6]。
完成现场地图构建后，需要在构建的地图上进行设备设施打点及机器人运动路径规划。高铁站环境复杂，需要规划机器人可运行区域，避免其误入设备区、卫生间、轨行区等位置。
机器人完成SLAM建图后，与高铁站电子地图进行比例映射，将机器人实时位置与运动状态与后台管理系统电子地图进行匹配，同时，后台根据当前位置与机器人运动目的地进行路径规划，给机器人发送控制指令，实现自动行驶[7]。
3.2 回声降噪、噪声抑制及6mic方位降噪技术
针对高铁站人流量大，声音嘈杂的特点，采用6mic方位降噪技术，机器人顶部安装有6个负责声音采集的传声器声卡，6个传声器收集到的声音先传输给USB声卡进行回声降噪处理，通过现场调试，修改滤波器系数，对回声进行估算，在话筒的输入信号中将回声估计值减去，达到消除回声的目的。
通过前期噪声抑制调试，分析背景噪声的强度和频谱，设置相应滤波器。人机交互时，通过区分讲话者的频谱和背景噪声频谱，滤波器将对背景噪声频谱进行抑制，对交互者声音频谱放行，达到噪声抑制的效果。
通过6个不同位置的传声器，可以识别对话者声音的输入方向，同时利用多个传声器收集到的信号可以增强或抑制某一方向传来的声音。利用这种方法，传声器阵列可以有效增强噪声环境中特定声音信号 [8]，实现多功能旅客服务机器人在高铁站嘈杂环境中的声音处理。6mic设计图如图3所示。
3.3 物联方案
为实现多功能旅客服务机器人自动通过闸机及自动呼叫乘坐直梯，其与车站现有设备设施都搭载了无线传输模块。无线传输模块可对传输的数据进行打包、检错、纠错处理，实现机器人远程控制闸机及直梯，进行迎宾导引及移动验检票服务。
4 结束语
多功能旅客服务机器人作为旅客服务的一部分，可实现与铁路其他相关系统的互联互通，解决既有旅客服务中耦合度高、信息点分布散的问题，实现铁路旅客服务信息的集成共享。通过机器视觉识别技术，提高旅客服务的交互主动性；通过智能语义理解，提高解决旅客问题过程中的智能化，在降低人工成本、提高时间效率的同时，通过机器学习及大数据分析机制，提升解决旅客问题的指向性、预测性；通过与直梯、闸机物联，实现旅客无感进站，减少旅客操作及物体接触，为旅客提供更加温馨舒适、便捷智能的乘车体验。同时，多功能旅客服务机器人作为智慧展示终端，为将来铁路智慧化，如安防巡检、环境提升、助老助残、信息传播等提供前端硬件支撑。
-
表 1 设备失效率和维修率
设备 独立失效率$ {\lambda _1} $/（次·h−1） 共因失效率$ {\lambda _2} $/（次·h−1） 维修率$ \mu $ SCU $ 1.26 \times {10^{{{ - }}5}} $ $ 3.90 \times {10^{{{ - 7}}}} $ 2 PIO $ 2.28 \times {10^{{{ - }}5}} $ $ 1.46 \times {10^{{{ - 6}}}} $ 2 DY $ 1.59 \times {10^{{{ - }}5}} $ $ 1.77 \times {10^{{{ - 6}}}} $ 2 CI-TC $ 1.20 \times {10^{{{ - }}5}} $ $ 1.04 \times {10^{{{ - 6}}}} $ 2 CI-GS $ 3.10 \times {10^{{{ - 6}}}} $ $ 1.98 \times {10^{{{ - 7}}}} $ 2 CI-LEU $ 9.20 \times {10^{{{ - 6}}}} $ $ 4.84 \times {10^{{{ - 7}}}} $ 2 CI-CBI $ 2.10 \times {10^{{{ - 6}}}} $ $ 2.33 \times {10^{{{ - 7}}}} $ 2 CI-TSRS $ 2.10 \times {10^{{{ - 6}}}} $ $ 1.58 \times {10^{{{ - 7}}}} $ 2 CI-ADTCC $ 2.10 \times {10^{{{ - 6}}}} $ $ 1.11 \times {10^{{{ - 7}}}} $ 2 
下载: 导出CSV
表 2 D-S证据理论获取的设备故障区间概率
设备 证据区间概率 /×10−5 SCU [1.225, 2.967] PIO [2.256, 3.998] DY [1.225, 2.967] CI-TC [1.592, 3.334] CI-GS [0.303, 2.045] CI-LEU [0.899, 2.641] CI-CBI [0.207, 1.949] CI-TSRS [0.205, 1.948] CI-ADTCC [0.204, 1.947]
下载: 导出CSV
表 3 超椭球模型约束的设备故障概率区间
设备 超椭球模型约束概率区间 /×10−5 SCU [1.491, 2.598] PIO [2.702, 3.482] DY [2.157, 2.714] CI-TC [1.843, 2.235] CI-GS [1.021, 1.299] CI-LEU [1.663, 1.857] CI-CBI [1.001, 1.141] CI-TSRS [1.023, 1.121] CI-ADTCC [1.038, 1.107]
下载: 导出CSV
表 4 TCC各设备的稳态可用度
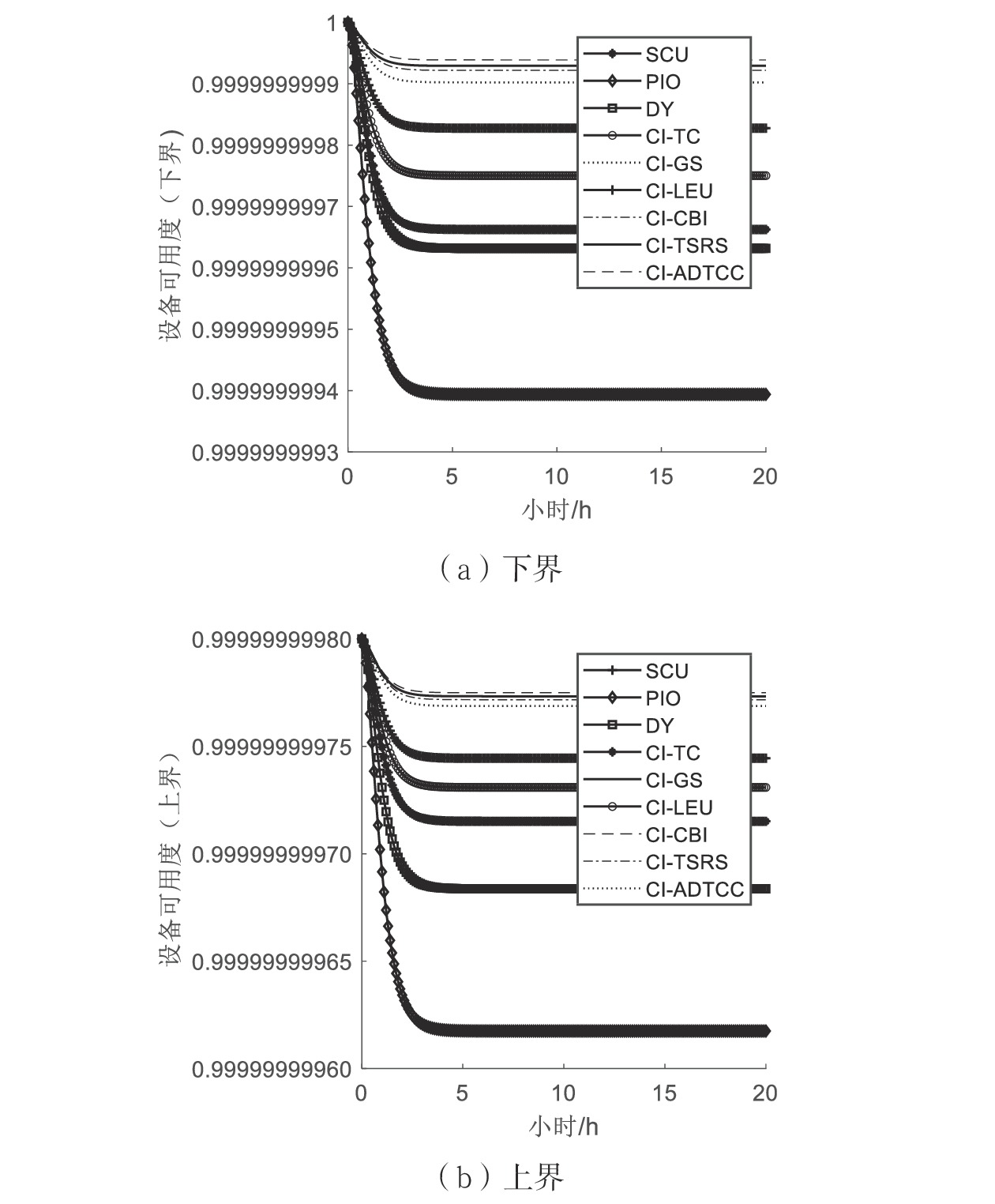
设备 稳态可用度 SCU [0.999 999 999 662 53, 0.999 999 999 888 85] PIO [0.999 999 999 393 81, 0.999 999 999 634 97] DY [0.999 999 999 631 72, 0.999 999 999 767 37] CI-TC [0.999 999 999 750 24, 0.999 999 999 830 17] CI-GS [0.999 999 999 915 63, 0.999 999 999 947 88] CI-LEU [0.999 999 999 827 58, 0.999 999 999 861 72] CI-CBI [0.999 999 999 934 91, 0.999 999 999 949 90] CI-TSRS [0.999 999 999 937 17, 0.999 999 999 947 67] CI-ADTCC [0.999 999 999 938 73, 0.999 999 999 946 13]
下载: 导出CSV
-
[1] 中国国家铁路集团有限公司. 全国铁路营业里程达到15.5万公里[ER/OL]. (2023-01-29)[2023-05-24]. http://www.china-railway.com.cn/xwzx/ywsl/202301/t20230129_125641.html. [2] Ismail A, Saidi L, Sayadi M, et al. Remaining useful life estimation for thermally aged power insulated gate bipolar transistors based on a modified maximum likelihood estimator[J]. International Transactions on Electrical Energy Systems, 2020, 30(6): e12358.
[3] 王 玺,胡昌华,裴 洪,等. 新研发光电产品的剩余寿命自适应预测方法[J]. 光学学报,2019,39(12):1223003. [4] 张正新,胡昌华,司小胜,等. 双时间尺度下的设备随机退化建模与剩余寿命预测方法[J]. 自动化学报,2017,43(10):1789-1798. [5] 张继冬,邹益胜,邓佳林,等. 基于全卷积层神经网络的轴承剩余寿命预测[J]. 中国机械工程,2019,30(18):2231-2235. [6] 徐洲常,王林军,刘 洋,等. 采用改进回归型支持向量机的滚动轴承剩余寿命预测方法[J]. 西安交通大学学报,2022,56(3):197-205. [7] 王 彪,秦 勇,贾利民,等. 监测数据驱动的城轨列车轴箱轴承剩余寿命预测[J/OL]. (2022-07-07)[2023-05-25]. http://kns.cnki.net/kcms/detail/51.1277.U.20220705.1807.008.html. [8] Marshall A W, Olkin I. Life distributions[M]. New York: Springer, 2007.
[9] Sikorska J Z, Hodkiewicz M, Ma L. Prognostic modelling options for remaining useful life estimation by industry[J]. Mechanical Systems and Signal Processing, 2011, 25(5): 1803-1836. DOI: 10.1016/j.ymssp.2010.11.018
[10] Park M, Rhee S. A study on life evaluation & prediction of railway vehicle contactor based on accelerated life test data[J]. Journal of Mechanical Science and Technology, 2018, 32(10): 4621-4628. DOI: 10.1007/s12206-018-0909-y
[11] 朱 涛,尹敏轩,王 超,等. 基于假设分布的重载货车关键结构剩余寿命预测方法[J]. 铁道学报,2022,44(4):19-26. DOI: 10.3969/j.issn.1001-8360.2022.04.003 [12] 王 康,齐金平,周亚辉,等. 基于离散时间贝叶斯网络的列控中心可靠性分析[J]. 中国机械工程,2021,32(4):390-398. [13] 江 磊,王小敏,蔺 伟. 基于动态贝叶斯网络的列控中心可靠性及可用性评估[J]. 交通运输系统工程与信息,2018,18(3):182-188,217. [14] Chen X Y, Fan J P, Bian X Y. Structural robust optimization design based on convex model[J]. Results in Physics, 2017 (7): 3068-3077. DOI: 10.1016/j.rinp.2017.08.013
[15] 史华东,陆宁云,许志兴,等. 基于D-S证据理论的城市轨道交通车辆车门亚健康融合诊断方法[J]. 城市轨道交通研究,2022,25(6):58-64,69. [16] 王啟鹏,周卫琪,景 鹏. 基于区间D-S证据理论的干线公交信号优先方案评价模型[J]. 公路交通科技,2019,36(10):114-120,151. [17] 葛 轶,周步祥. 基于超椭球贝叶斯网络的配电系统可靠性评估[J]. 电测与仪表,2017,54(1):22-26. [18] 齐金平,王 康,周亚辉,等. 基于Markov的列控中心可用度及剩余寿命预测[J]. 中国安全科学学报,2021,31(10):54-61. [19] 蒋乐天,徐国治. 故障树模型与Markov模型的关系及转换[J]. 系统工程与电子技术,2003,25(11):1441-1444. [20] 国家铁路局. 列控中心技术条件:TB/T 3439-2016[S]. 北京:中国铁道出版社,2016. -
期刊类型引用(3)
1. 黄凌杰. 服务机器人室内投递的全局路径规划仿真. 福建电脑. 2023(03): 104-106 . 
百度学术
2. 王睿，杨元元，任秋呈. 城市轨道交通站内服务机器人的拟人化设计研究. 工业设计. 2023(11): 157-160 . 百度学术
3. 戴彦华，陈天煜，支涛，李全印. 服务机器人与铁路客运站既有系统设施融合应用的设计与实现. 铁道运输与经济. 2022(09): 77-82 . 百度学术
其他类型引用(1)
计量
- 文章访问数: 45
- HTML全文浏览量: 9
- PDF下载量: 11
- 被引次数: 4
