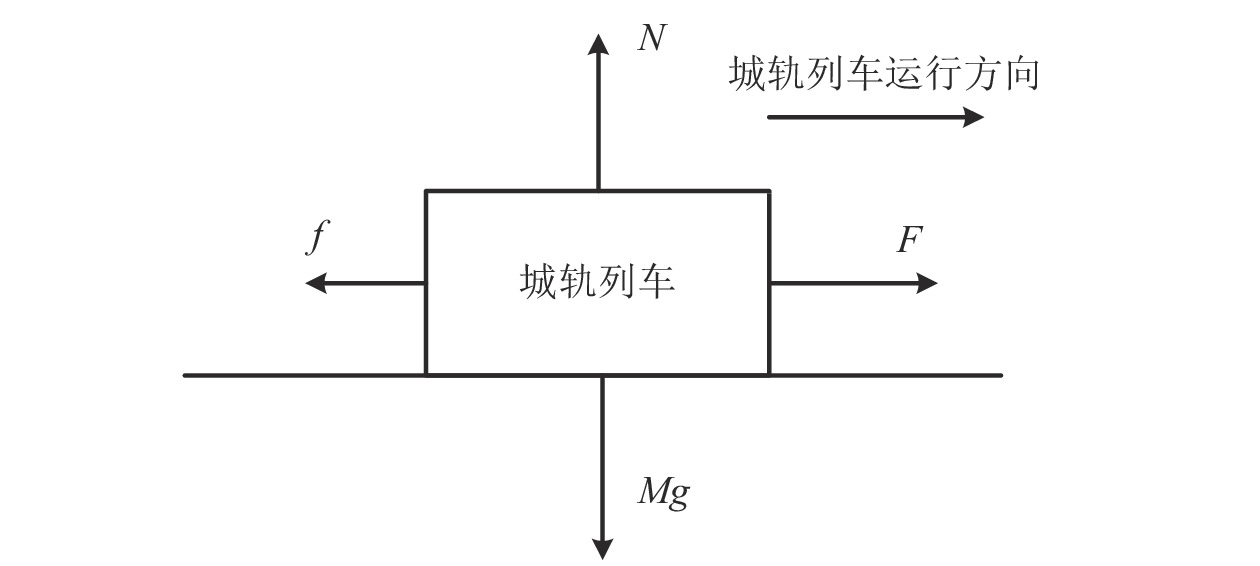
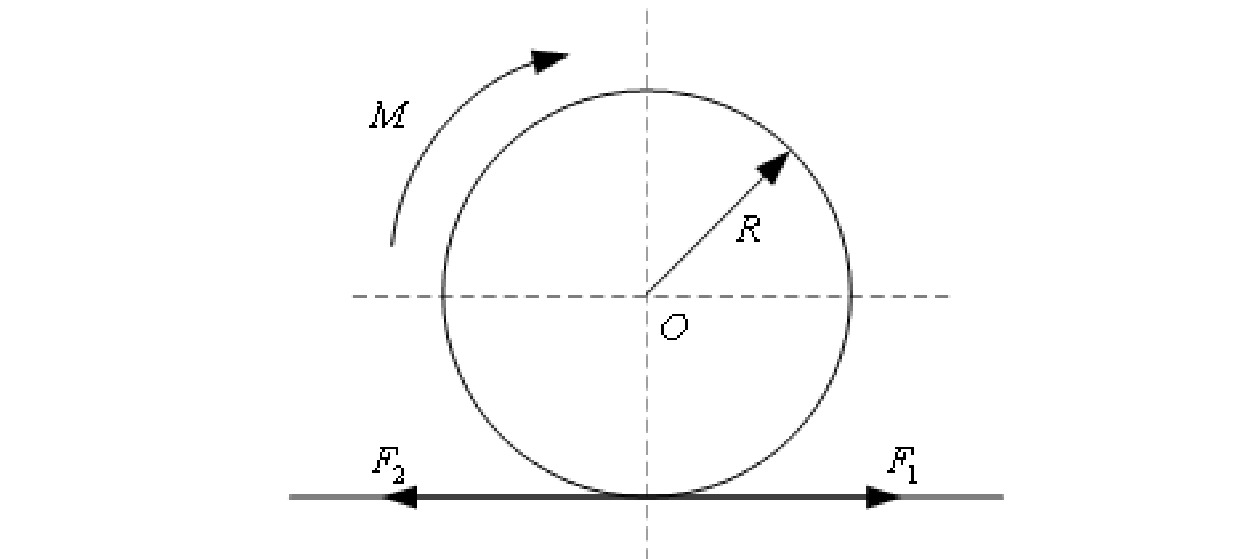
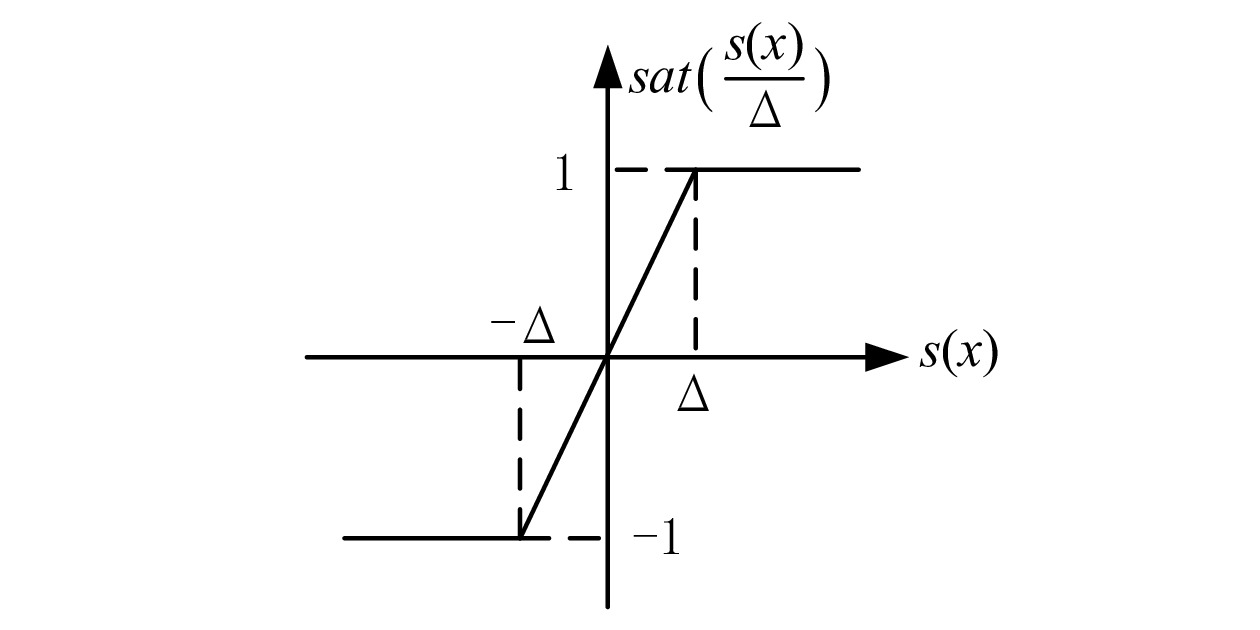
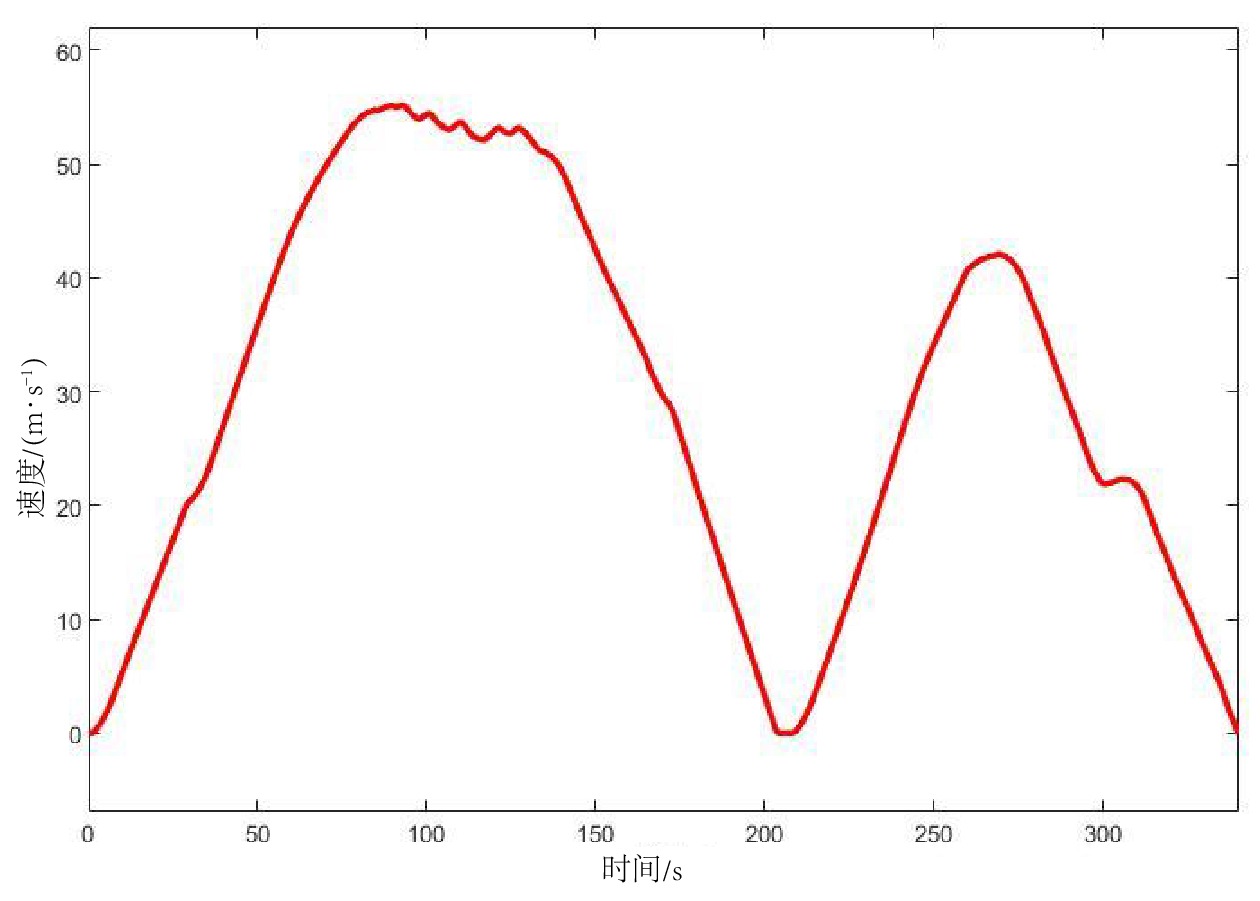
Sliding mode adaptive speed tracking control based on single-particle dynamic model of urban rail train
-
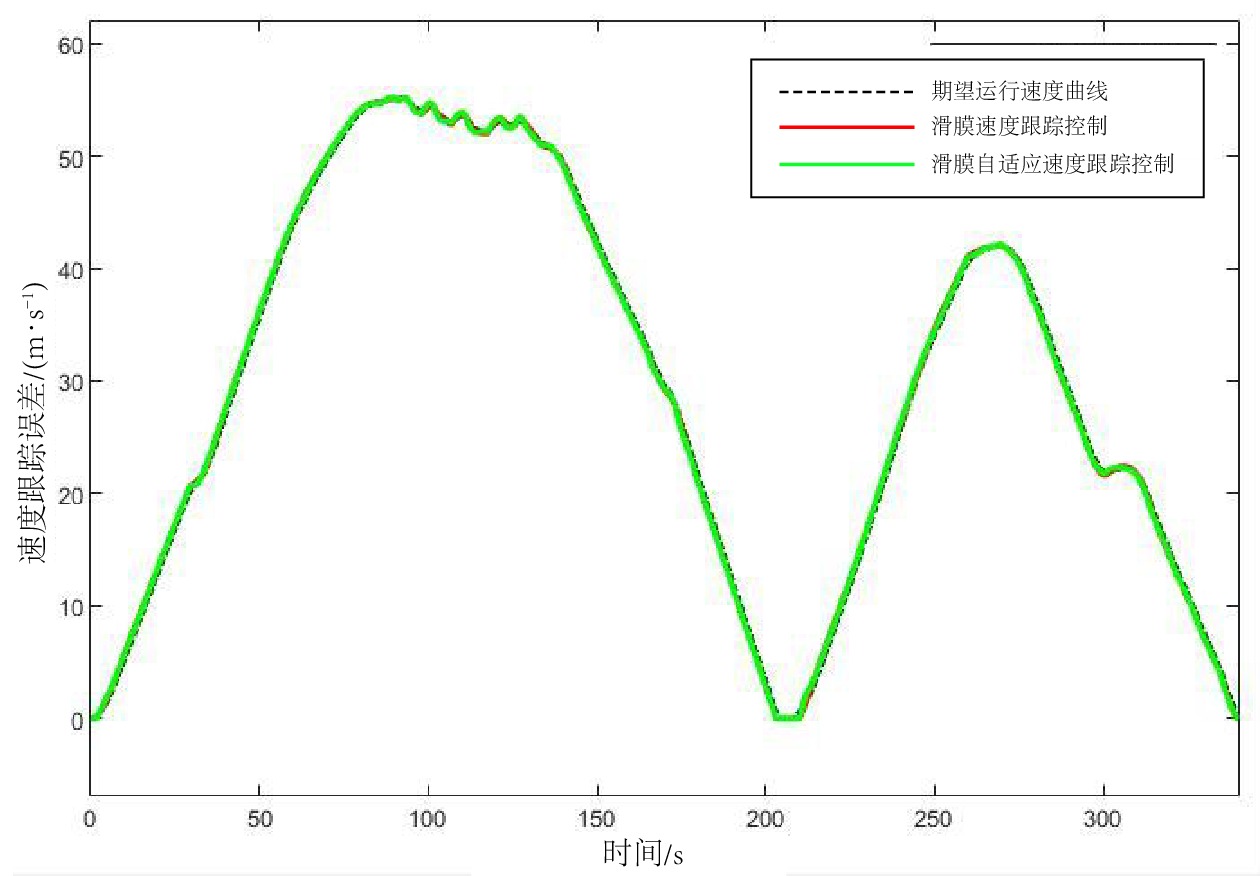
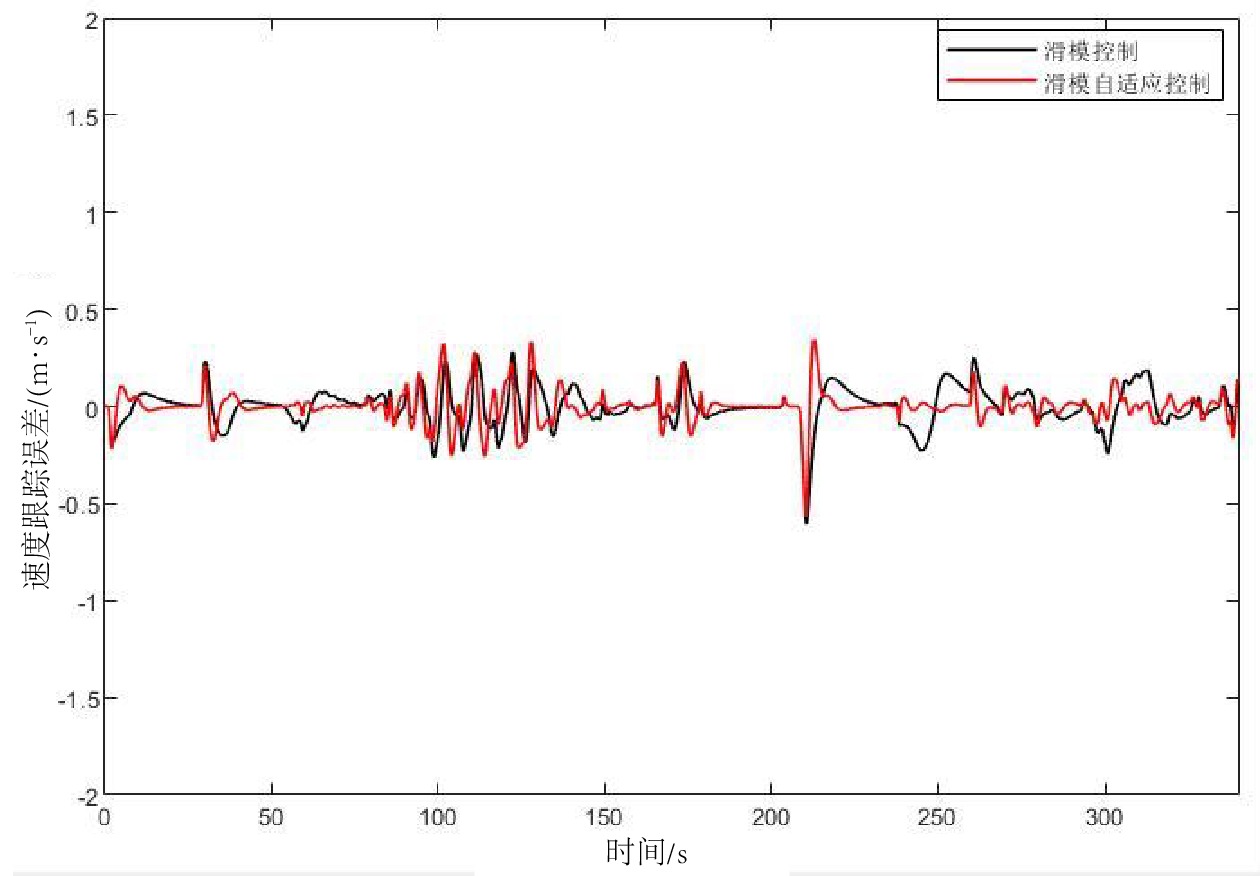
摘要: 实现城市轨道交通(简称:城轨)列车自动驾驶的关键是实现城轨列车运行速度曲线的跟踪控制。文章通过对城轨列车的运行进行受力分析,建立城轨列车单质点动力学模型,并设计了滑模自适应速度跟踪控制器,实现对城轨列车运行速度曲线的跟踪控制。以广州22号线城轨列车数据为研究对象,进行仿真试验,验证了滑模自适应速度跟踪控制器的有效性。Abstract: The key to implementing automatic driving of urban rail transit trains is to track and control the speed curve of urban rail train operation. This paper analyzed the forces acting on the operation of urban rail train, established a single-particle dynamic model of urban rail train, and designed a sliding mode adaptive speed tracking controller to implement tracking control of the speed curve of urban rail train operation. The paper also took the data of urban rail train on Guangzhou Line 22 as the research object and conducted simulation experiments to verify the effectiveness of the sliding mode adaptive speed tracking controller.
-
铁路枢纽是铁路路网技术作业高度集中的关键区域。当前,全国枢纽总图方案正在进行新一轮调整和布局,对铁路枢纽规划和设计提出新的要求,铁路枢纽能力评价可为铁路枢纽总图方案设计提供决策依据。研究铁路枢纽能力利用的评价方法,是铁路枢纽规划和总图设计的核心问题之一,对实现路网和枢纽合理布局、提升运输效率和品质具有重要理论和现实意义。
针对铁路枢纽总图评价,国内外学者开展不少的相关研究工作。何世伟等人[1]提出路网总体运输能力及有效能力、潜在能力的概念;何志工[2]立足于铁路枢纽总图内涵,从功能定位以及客运、货运、编解、枢纽能力等方面提出铁路枢纽规划方案的评价指标体系;雷中林[3]采用主观权重和熵权结合法构建铁路枢纽规划方案的指标体系和评价方法;黄隆飞[4]采取功能综合分析和定量定性结合方法建立铁路枢纽从宏观层面到微观层面的评价指标体系,采用模糊分析方法进行评价;文献[5]~文献[7]分别采用神经网络方法、多级优度物元方法、VISSIM仿真对地铁车站、地铁换乘站和客运枢纽进行评价;文献[8]和文献[9]分别探讨综合客运枢纽的总体架构和枢纽调度指挥系统设计问题。
可以看出,较多研究均关注到铁路枢纽作业环节繁多、能力构成要素复杂的问题。如何使评价方法覆盖主要作业环节和能力构成要素,且对不同规模等级和不同客货运输结构的铁路枢纽具有普适性,是铁路枢纽能力利用率评价的难点所在。
1 铁路枢纽能力利用率评价指标体系
1.1 评价指标体系设计原则
从铁路枢纽能力利用率评价问题出发,评价指标体系设计需遵循以下原则。
(1)全面反映铁路枢纽能力利用的状况:评价指标体系应服务于铁路枢纽总图规划的设计目标,每项评价指标应能反映铁路枢纽系统运输能力在某一方面的典型特征,指标间具有互补性,整体能够综合反映铁路枢纽运输系统的能力利用状态;
(2)具有与铁路枢纽能力要素构成相对应的层次性:指标体系具有逐层展开的层次性特征,每项评价指标及所属的子系统、枢纽元素间具备明确的从属关系和严格的层次结构;
(3)评价指标的数量规模适度:评价指标的选择不应过于庞杂,要注意区别主次与轻重,选取能够反映铁路枢纽总图规划整体状况、作业特点的指标项,保持评价指标体系的简洁性;
(4)评价指标定义和口径明确:每项评价指标应定义明确,规定其具体统计方式和统计范围,便于数据收集和量化处理。
1.2 评价指标体系构建思路
按照作业性质,铁路枢纽可划分为客运、货运、行车、编解等子系统,各子系统又包括若干个车站、区间等构成要素。枢纽内的能力利用率可按照各构成要素所包含的作业环节设置评价指标。目前,尚无普遍公认的铁路枢纽能力利用率评价指标体系,但铁路运输管理部门已形成针对铁路各作业环节较为完备的能力利用状况统计指标。以这些统计指标为基础,构建铁路枢纽能力利用率评价体系的基本思路如下:
(1)兼顾客货运输和不同铁路枢纽的特点,依据枢纽子系统的构成要素和作业环节设计评价指标,使得评价指标能够更全面的反映枢纽整体状况并发现枢纽存在的问题;
(2)重视点线能力协调和枢纽编解作业,将行车子系统划分为车站和线路区间2个组成部分,从两者关系角度突出点线能力,并从枢纽编解子系统角度着重考察枢纽编解作业均衡性;
(3)针对枢纽子系统,从其包含的车站、区间等枢纽要素,以及相关的技术设备、作业环节出发,选取具体的能力利用率指标项。
为此,从铁路枢纽的客运、货运、解编子系统以及行车子系统的区间和车站5个方面提出评价指标集,形成枢纽子系统—构成要素—评价指标3个层次的枢纽能力利用率评价指标体系,如图1所示。
2 铁路枢纽能力利用率评价方法
2.1 能力利用率指标的评价得分设计
一般评价问题的指标项按其理想值位置和优劣分布规律,一般分为成本型、效益型、适中型3类。而铁路枢纽能力利用率均属于适中型指标,取值区间为
$[0,100\% ]$ 。相对于能力利用率具体数值,通常评价者关心的是能力利用的合理程度。各指标项能力利用率均存在最理想的取值区间,能力利用率的评价得分值从理想取值区间向大小两侧降低。为此,可基于能力利用率的适中型特征构造指标的分段得分函数。对某一指标项的能力利用率
$ x $ ,其理想值为$\left[ {{{\underline x }^*},{{\bar x}^*}} \right]$ ,取值空间为$\left[ {{{\underline x }},{{\bar x}}} \right]$ ,其得分函数$r\left( x \right) $ 可构造如下:$$ r\left( x \right) = \left\{ {\begin{array}{*{20}{c}} {{r_1}}&{\underline x < x \leqslant {x_1}}\\ \cdots & \cdots \\ {{r^*}}&{{{\underline x }^*} < x \leqslant {{\bar x}^*}}\\ \cdots & \cdots \\ {{r_k}}&{{x_{k - 1}} < x \leqslant \bar x} \end{array}} \right. $$ 其中,
$k $ 为得分函数的分段数;${r_1}, \cdots ,{r_k} $ 为各分段的得分值;$ {r^{\rm{*}}} $ 为最理想得分值。考虑到指标项的实际含义和能力特点,理想取值区间、得分函数可按指标项区别设置。表1为某指标的五分制得分函数取值表。在表中,对每一量度值引入“+”、“−”符号标明其与理想值的偏离方向,以便能够直观准确判断出枢纽能力利用率存在问题。这些符号并不参与评价计算,以避免相互抵消的问题发生。
表 1 某指标项的评价得分取值能力利用率(%) 得分取值 [0, 45] −1 (45, 55] −2 (55, 65] −3 (65, 75] +5 (75, 85] +4 (85, 95] +2 (95, 100] +1 2.2 层次化的评价指标权重设计
对上述铁路枢纽能力利用率评价指标体系,可按层次设置分层权重体系,以便有效降低权重设置难度。分层权重体系主要包括各子系统间评价权重、各子系统内构成要素的权重和子系统指标项间权重。
客运、货运、行车(车站、区间)和编解等子系统权重之和为1。各子系统间的评价权重可参考运输量(客运量、货运量、改编车流比重)来综合标定。
每一子系统内各构成要素的权重,可按照某种运输量标准确定。如客运子系统内各客运站的权重可按照其到发旅客量占比设置;货运子系统内货运站的权重可按照其装卸货物量占比设置;行车子系统各车站依据接发列车数设置各车站权重,依据区间行车量设置各线路区间权重。
指标权重可按照子系统独立设置。每一子系统内各指标间权重之和为1,每一指标权重可根据作业地位、作用和评价目的进行设置。
2.3 评价算法
根据问题特征和指标体系特点,以基于各指标的评价得分和层次化的评价指标权重设计为基础,设计铁路枢纽能力利用率评价方法,具体步骤为:
(1)搜集和确定铁路枢纽各构成元素的每一评价指标的能力利用率,并根据利用率数据标定评价得分;
(2)建立铁路枢纽内子系统、构成要素和指标项的层次关系,设置各层次权重;
(3)逐个计算铁路枢纽每一子系统评价得分,对子系统各构成要素指标的得分加权求和即可获得该子系统的评价得分,并累加记录各构成要素每一指标在子系统评价得分中的贡献率;
(4)按照各个子系统的权重系数,对各子系统评价得分的加权求和即可获得铁路枢纽能力利用率的总体评价得分,输出的评价结果包括枢纽总体评分、各子系统得分、具有较大贡献率的能力利用瓶颈点数量、位置和排序等内容。
铁路枢纽能力利用率评价方法的算法流程如图2所示。
3 实例分析
采用C#语言设计开发了铁路枢纽能力利用率评价软件,包括能力利用率基础数据管理、多层次权重设置和能力利用率综合评价3个功能模块。
以郑州枢纽某一年度总图方案为例,依据客货运输相关数据,运用本文提出的评价方法,评价分析其能力利用率。
郑州枢纽是由京广线、陇海线、京广客运专线、徐兰客运专线等干线交汇形成双十字形铁路枢纽,在路网中具有举足轻重的地位。根据各子系统在枢纽中的作用和作业量,适当突出编解、行车子系统的影响,设置客运、货运、编解子系统以及行车子系统中的车站和线路区间权重分别为0.20、0.10、0.30、0.20、0.20。
计算车站和线路区间评分分别为3.03和1.86,按其权重加权可计算枢纽内行车子系统的得分为2.44。同理,计算各子系统和枢纽整体的评价得分,结果如图3所示。枢纽总体评价得分为2.33,能力利用率均值为57.24%。根据最终的评价得分可以看出,虽然郑州枢纽能力利用率总体能力利用率均值并不高,但各子系统能力得分差异较大。
将各枢纽作业环节按其对枢纽总体评价得分的贡献率进行排序,确定枢纽能力的瓶颈点。郑州枢纽能力瓶颈点的能力利用率和贡献率及其排序见表2。
表 2 郑州枢纽的能力瓶颈点情况分析排序 按能力利用率排序 利用率(%) 按贡献率排序 贡献率 1 陇海线铁炉至关帝庙区间通过能力 100 郑州北站下行驼峰解体能力 2.94 2 陇海线莆田至莆田西区间通过能力 98.4 郑州北站上行驼峰解体能力 2.72 3 郑州北站下行驼峰解体能力 97.9 陇海线铁炉至关帝庙区间通过能力 1.80 4 京广线广武至东双桥区间通过能力 97.5 陇海线莆田至莆田西区间通过能力 1.77 5 陇海线占杨至莆田区间通过能力 95.3 京广线广武至东双桥区间通过能力 1.76 6 郑州北站上行驼峰解体能力 90.8 陇海线占杨至莆田区间通过能力 1.72 可以看出,这些瓶颈点的能力利用率均超过90%,各瓶颈点的能力利用率大小和贡献率排序存在较大差别。利用率最高的陇海线铁炉至关帝庙区间的通过能力,其贡献率仅列第3,而郑州北站下、上行驼峰解体能力的贡献率最高,对枢纽能力的制约作用较为明显。
4 结束语
将铁路枢纽划分为客运、货运、行车、编解等子系统,构建子系统−构成要素−评价指标3个层次的指标体系;根据铁路枢纽的层次化结构特征,提出指标项评价得分函数和层次化权重设置方法,建立基于子系统划分的铁路枢纽能力利用率评价方法。
基于所设计的评价指标体系和评价方法,开发了铁路枢纽能力利用率评价软件,利用该软件对郑州枢纽能力利用率进行计算和分析。
本文提出的评价方法能够克服铁路枢纽系统构成复杂、作业环节众多的困难,全面分析评价铁路枢纽能力利用状况,有效识别制约铁路枢纽能力的瓶颈。但评价方法中权重参数的合理设置问题,以及如何将客、货车流径路等能力要素引入评价方法,均尚需进一步研究。
-
[1] 杜海宾,王 瑞,姜 正,等. 货运机车自动驾驶系统贯通试验控制研究及应用 [J]. 铁路计算机应用,2022,31(5):60-64. [2] 赵 阳,张 萍. 高速铁路自动驾驶技术研究与展望 [J]. 铁道通信信号,2019,55(S1):75-80. [3] 李中奇,丁俊英,杨 辉,等. 基于控制器匹配的高速列车广义预测控制方法 [J]. 铁道学报,2018,40(9):82-89. [4] 丁 盼. 基于多质点模型的高速列车自适应速度跟踪控制[D]. 南昌: 华东交通大学, 2021. [5] 宋 琦. 高速列车的鲁棒自适应及容错控制[D]. 北京: 北京交通大学, 2014. [6] Song Y D, Song Q, Cai W C. Fault-tolerant adaptive control of high-speed trains under traction/braking failures: a virtual parameter-based approach [J]. IEEE Transactions on Intelligent Transportation Systems, 2014, 15(2): 737-748. DOI: 10.1109/TITS.2013.2290310
[7] Lin X, Dong H R, Yao X M, et al. Neural adaptive fault-tolerant control for high-speed trains with input saturation and unknown disturbance [J]. Neurocomputing, 2017(260): 32-42. DOI: 10.1016/j.neucom.2017.02.083
[8] 袁佳希. 列车在线辨识与预测控制研究[D]. 杭州: 浙江大学, 2017. [9] 任一凡,孙后环,刘 陈. 基于滑模控制算法的自适应跟车巡航研究 [J]. 机械与电子,2023,41(1):59-64. [10] 李中奇,周 靓,杨 辉. 高速动车组数据驱动无模型自适应控制方法 [J]. 自动化学报,2023,49(2):437-447. [11] 刘 豹, 唐万生. 现代控制理论[M]. 3版. 北京: 机械工业出版社, 2013: 164-165. [12] 刘金琨. 滑模变结构控制MATLAB仿真: 基本理论与设计方法[M]. 3版. 北京: 清华大学出版社, 2015: 56-57. -
期刊类型引用(1)
1. 史方圆,宗智诚,马毅华,傅鹏,吴文波. 基于雷视融合的涉铁工程防侵限监测系统的设计与实现. 铁路计算机应用. 2024(11): 32-37 .  本站查看
本站查看
其他类型引用(0)





 下载:
下载: