截至2022年，我国高速铁路总运营里程已达4.2万 km，日均开行动车组超4000列，年客运发送量超30亿人次，具有开行范围广、运行环境多变、开行列数多、旅客出行量大、客流结构复杂、准时性要求高等特点。

调度集中（CTC，Centralized Traffic Control）系统是调度中心调度员用于对某一调度区段内信号设备进行集中控制，对列车运行实施直接指挥和管理的技术设备。伴随着我国高速铁路建设的推进，高速铁路CTC系统经历了从线路别小规模集成发展为路网性大规模集成的发展历程，已达到较高的信息化和集成化水平，是高速铁路高效调度指挥、列车有序运行的关键支撑。

本文结合既有CTC系统的现状及存在的问题，针对高速铁路行车调度指挥现实需求，提出高速铁路智能CTC系统构想，初步探讨相关关键技术，以期推动我国智能高速铁路的发展^[1]。

1   高速铁路CTC系统现状及存在的问题

1.1   高速铁路CTC系统应用现状

CTC系统是铁路信息化建设的重要组成部分。2003年，我国第一条高速铁路秦皇岛—沈阳客运专线（时速200 km以上）开通了CTC系统，并于2010年改造为分散自律型CTC系统。随着我国高速铁路网的不断拓展，高速铁路CTC系统实现了路网性大规模集成，形成中国铁路总公司调度中心、铁路局调度中心CTC系统和车站CTC子系统3级架构。

中国铁路总公司调度中心负责全国高速铁路网综合调度指挥，通过采集全国18个铁路局所有高速铁路的实时运输信息和设备数据，监督全国高速铁路网的列车运行状态；监控各主要干线、分界口、大型客站、枢纽的高速列车总体运行状态，完成高速铁路列车运行统计分析，跟踪重点列车及试运行列车位置，确认现场设备状态，并纳入全国铁路调度指挥系统数据库。

铁路局调度中心系统实时自动采集列车运行及现场设备状态信息，实现列车运行实时追踪、无线车次号校核、正晚点统计分析、列车实际运行图自动绘制、阶段计划人工和自动调整、调度命令及列车运行计划下达等功能^[1]。

车站子系统接收调度中心子系统下达的列车运行计划，根据列车运行计划完成进路选排、冲突检测、控制输出等核心功能，完成调车作业计划编制及调车作业进路控制。

1.2   既有高速铁路CTC系统存在的主要问题

目前，高速铁路CTC系统已达到较高的信息化和集成化水平^[2]，受限于现有铁路技术装备水平等诸多因素，既有CTC系统的智能化程度依然不高，在实际应用中存在一些问题。

1.2.1   列车运行计划调整效率较低

目前，日常高速铁路列车运行调度主要是通过行车调度员与高速列车司机之间的协同配合来完成的。在基于GSM-R网络的GPRS通信、无线调度传输设备、车载无线调度通信设备、轨道电路以及地面应答器等行车装备的支持下，行车调度员与高速列车司机之间能够即时传递行车指令和交互信息，相互配合完成高速列车的运行控制和计划调整。在这种作业模式中，主要依靠调度员进行人工判断，对列车运行图做出即时的局部调整，制定阶段计划并下达，列车运行计划调整往往存在较高延时，而且在突发情况时难以考虑全局优化，无法得到最优的运行图调整计划，不利于高速铁路运输组织的整体优化。

1.2.2   非正常情况下过度依赖人工操作

当遇大风、暴雨、降雪等恶劣天气时，必须对列车限速运行，甚至封锁线路临时检修以保证行车安全，严重影响列车运行秩序。此外，当列车在始发/终到站有后续交路，或在车站依次等待作业线路空闲，容易造成列车晚点，并在铁路网中迅速传播，最终导致大面积列车晚点，进一步给列车调度员带来大量的额外调整工作。列车调度员不得不按照列车速度等级、运行等级、先跨局后管内等原则，逐一安排列车运行顺序，办客站变更旅客列车办客股道（后续还涉及安排客运如何放客等作业），调整车底交路、机班交路等，完全依靠人工调整，效率低下且容易出错。

1.2.3   应急处置响应不够迅速

高速铁路应急处置往往需要由车、机、工、电、辆等多专业协同完成。目前，虽然各专业都有相应的业务系统提供支持，但部分业务系统仍处于独立封闭运行，不同专业之间的信息交互仍然需要依赖人工通话完成信息传递。由于我国高速铁路网构成复杂，调度与控制多极耦合、多子系统交互、模型多、参数多，难以采用单一的应急处置模型，当出现影响行车的事故时，列车调度员作业压力极大，多环节经由人工操作，造成应急处置效率较低，难以满足高速铁路高准时率的现实要求。

1.2.4   列车与调车作业协同困难

在既有CTC系统中，列车调度员仅负责列车运行调整，在客货共线铁路、高速/普速铁路交汇、存在货场专用线的车站，调车作业时仍需车站值班员操作，对于由中心操作的车站，要求车站在调车作业时转为车站操作或非常站控模式，作业完毕后再转为原先的模式。频繁转换车站工作模式不仅会降低接发列车和调车作业效率，还极大地影响CTC系统的稳定性，给高速铁路运输安全带来极大的隐患。

2   高速铁路智能CTC系统构想

2.1   设计目标

（1）提高列车运行计划调整效率：通过列车运行计划自动编制、列车运行图实时自动调整、阶段计划自动校验、办客站股道自动选排等功能，由智能化系统代替人工完成调度工作中大量重复性作业，如调整列车区间运行点，电力/内燃机车属性设置，旅客/货物列车技术停点变更通过、办客站旅客列车变更固定股道等，大幅减少列车调度员工作量，降低人工操作带来失误。

（2）实现非正常情况下列车运行调整自动化：通过构建高速铁路行车数据大数据综合平台，实现车、机、工、电、辆等部门各类信息汇总，有助于统筹安排，实现各工种作业“一条龙”式联动调整。例如，当出现动车组晚点时，可通过该平台的信息共享，12306旅服系统能够实现列车运行数据即时更新，机务段车底交路自动顺延或启用热备，车站终端自动生成换乘旅客改乘或改签方案等；系统自动生成多个可行调整方案后，列车调度员仅需点击鼠标选择合适的方案，即可实现快速选择最优调整计划，并发送给各工种作业人员，大幅减少人工操作量。

（3）实现调车作业自动化：在列车进路自动排列技术的基础上，进一步实现调车进路自动排列、调车计划自动执行等功能，选择在基本图中列车分布较少时间点进行调车作业，有调车作业车站增设隔开设备，实现列车进路和调车进路的完全隔离，有助于保障运输安全，整体提高铁路运输效率。

2.2   系统架构

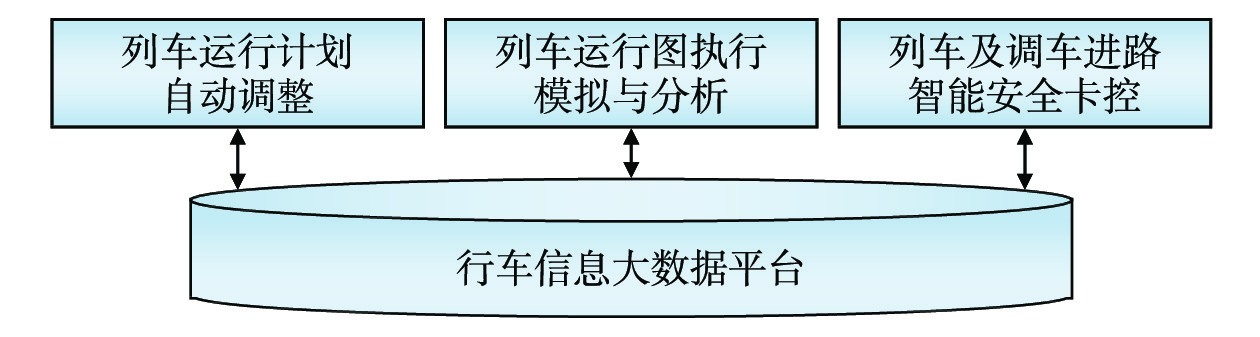
高速铁路智能CTC系统^[3]通过构建高速铁路全网行车信息大数据平台，实现车、机、工、电、辆等部门间信息共享和业务协同，能够根据实时采集的列车运行信息和车站设备状态，由计算机自动生成列车运行调整计划，通过云计算等技术实现列车运行图执行模拟与分析，实现列车及调车进路的智能安全卡控；高速铁路智能CTC系统架构如图1所示。

图  1  高速铁路智能CTC系统架构示意

下载: 全尺寸图片 幻灯片

2.3   主要功能

2.3.1   行车信息数据共享

在大数据、物联网、北斗卫星导航、云计算等先进技术的支撑下，构建高速铁路行车信息大数据平台^[4-6]，加强车、机、工、电、辆多专业各部门间信息交互，支持流程化应急处置，提供列车运行动态综合展示等功能，实现作业流程化、规范化，全面兼顾区域性调度和局部调度作业要求，全面把握列车运行动态，实现高速铁路运输组织最优化^[7]。

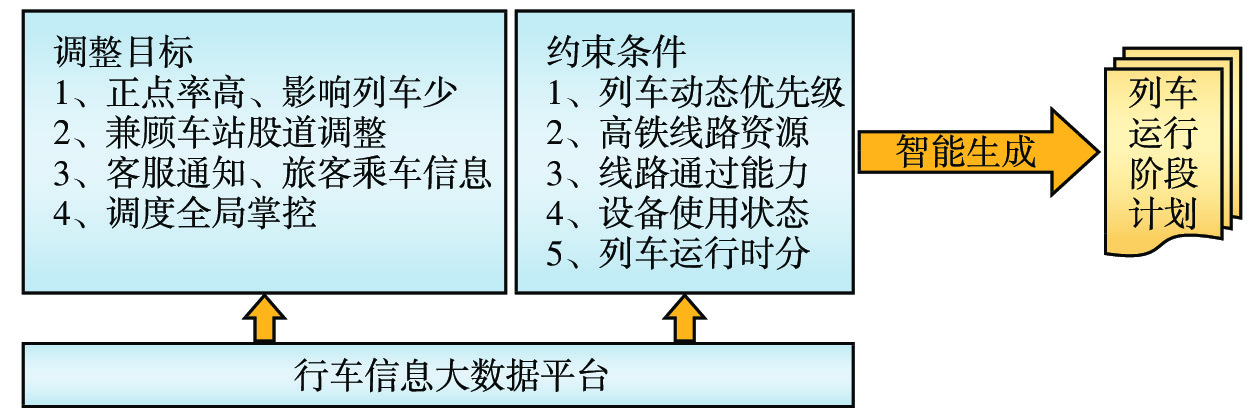
2.3.2   列车运行计划自动调整

在大风、暴雨、降雪等恶劣天气或设备故障等应急情况下，系统在行车信息大数据平台的支持下，列车运行自动调整算法（其框架如图2所示）按照调度员设定的调整目标和相应约束条件，快速、高质量地完成列车运行阶段计划的自动调整^[8-9]，不但可减轻调度员的劳动强度，提高列车调度员的应急处置效率，还能够降低应人工调整延时带来的不利影响，更好地保障列车运行安全，提高高速铁路运营效率。

图  2  列车运行计划自动调整算法框架示意

下载: 全尺寸图片 幻灯片

2.3.3   列车运行图执行模拟与分析

随着高速铁路新线的不断开通以及设备的不断更新，高速铁路运输组织对列车调度员的调度指挥水平提出更高要求。列车运行图执行动态模拟功能模块作为调度员调整列车运行的辅助插件，可结合列车运行实时状态和设备实时工况，快速推演列车运行图的执行过程，生成多个可选的列车运行计划调整方案，并提供优劣分析、行车安全分析，大幅提高列车调度员调整列车运行计划的精度及效率。

2.3.4   列车及调车进路智能安全卡控

通过增设或改进现场信号、道岔等设备，以及融合现有调度集中系统相关信息，深度拓展车站子系统自律卡控条件，增加固定进路卡控、调车作业卡控、车站（场）满线卡控、场联进路自动办理、无线发车预告、车次号有效性卡控等控制逻辑，完成列车运行计划和调车作业计划可执行性判别、列车和调车进路自动排列、进路智能安全卡控等功能，进一步提高行车安全保障能力。

3   关键技术

3.1   基于大数据的信息共享及智能分析技术

全面采集列车实时运行状态和现场设备情况，从图、车、人、天、地5个维度，依据高速铁路相关专业部门规章制度和作业标准等，分析列车运行秩序干扰因素，研究列车早晚点的扩散机理、调整策略的评估方法^[10]。

智能分析技术的应用重点关注员工行为分析和线路运能分析。其中，员工行为分析基于调度员和车站值班员历史操作记录和深度学习算法，建立员工行为分析模型，能够自动识别高风险操作行为，并提出个性化的员工技能强化培训建议。线路运能分析基于列车运行和线路设备长期运营数据，建立线路能力分析模型，分析制约运能提升的关键环节，以实现智能CTC系统的优化。

3.2   列车运行计划的协调与优化技术

在我国既有高速铁路网络化运营环境下，要充分考虑不同调度区域、不同线路间相互协调配合，在统一的调度指挥系统支持下，实现运力资源的统一安排和调配，保持全国高铁路网调度指挥的高度统一性^[11]。为此，需要深入研究全国铁路网不同调度区域间列车运行计划的编制与执行的协调机制，以及列车运行计划和各调度台运行图之间的实时互动与协调。另外，研究列车运行延误的网络传播分析与预测方法、应急处置场景下的调整策略优化方案，以实时掌握全国高速铁路网整体运行状况；当遭遇突发事件时，能够高效地调度各种资源，及时快速反应。

3.3   列车运行图执行模拟与分析

基于高速铁路日常列车运行计划调整模型、非正常情况下应急处置调整模型和历史调整信息等数据，结合实时采集的列车运行状态及现场设备情况，建立与真实环境一致的数字孪生环境，通过大量推演计算，模拟列车运行图执行过程，自动生成多个可供选择的列车运行阶段计划调整方案，并提供不同方案的优劣分析、行车安全分析等评价信息，辅助列车调度员完成列车运行计划调整；此外，还能对新基本图方案、线路改造方案进行执行模拟，并给出相应的评价和建议。

3.4   不同等级列车共线运行条件下自恢复和自适应机制

在高速铁路高密度公交化运营条件下，需要灵活适应市场需求，提供丰富的列车运行秩序控制模式，为调度员提供各种简单易行的自动化干预手段^[12-13]，研究人工干预方式和自动排列进路机制，强化市场化、经济化运营，为铁路提质增效创造强有力的支持。

3.5   基于可信动态感知的调度智能协同

通过可信感知技术（PSCADA、FAS、BAS、PA、CCTV等）与调度智能协同技术的相互融合，对列车运行状态和突发事件进行实时监测、识别和分析，并基于列车运行计划协调与优化技术，提供统一的数据显示和操作界面，使调度员能够以快捷方式建立调度指挥决策模型，达到高效优化正常作业和应急处置的效果。

4   结束语

结合高速铁路列车调度工作实践及高速铁路CTC系统使用体验，分析了既有高速铁路 CTC系统存在的不足之处，针对我国高速铁路高质量快速发展的需求，提出高速铁路智能CTC系统的构想，描述了新型智能CTC系统的设计目标和主要新增功能，初步探讨了实现高速铁路智能CTC系统的若干关键技术。高速铁路智能CTC系统能够更好地满足我国高速铁路运输组织需求，为铁路各工种尤其是调度员提供更为便捷、高效、安全的工具，将促进我国高速铁路安全、优质、快速发展，为兴路强国提供更为坚实的技术保障。

高速铁路智能CTC系统将为高速铁路运输调度指挥工作带来基于网络化、智能化的调度决策和运行控制手段，实现运营过程可信动态感知、路网运输能力动态调配、调度指挥管控智能协同、安全隐患辨识预警等应用效果，实现全国铁路网多专业岗位的高效协同，形成我国高速铁路更为高效、灵活的列车运行调度指挥模式。

目前，我国铁路系统对物联网、大数据、北斗卫星导航、云计算、机器学习等新技术的应用正处于起步阶段，需要不断进行深入探索，有效应用新技术对列车运行调度指挥业务链进行持续改进，不断提高高速铁路CTC系统的智能化、实用性、可靠性和安全性。