动车组受电弓可靠性数据分析

薛康; 齐金平; 徐安策; 周亚辉; 李少雄

doi:10.3969/j.issn.1005-8451.2021.12.04

动车组受电弓可靠性数据分析

薛康^1,,
齐金平^{1, 2, 3,},
徐安策⁴,
周亚辉¹,
李少雄¹

1.
兰州交通大学　机电技术研究所，兰州　730070
2.
甘肃省物流及运输装备信息化工程技术研究中心，兰州　730070
3.
甘肃省物流与运输装备行业技术中心，兰州　730070
4.
中国铁路兰州局集团有限公司　办公室，兰州　730015

基金项目: 国家自然科学基金项目（71861021）；甘肃省重点研发计划项目（17YF1FA122）；甘肃省高等学校科研资助项目（2018A-026，2018C-10）；中国铁路总公司科技研究开发计划项目（2015T002-D）

详细信息

作者简介:
薛　康，在读硕士研究生

齐金平，副教授

中图分类号: U266.234 : TP39
计量
- 文章访问数: 144
- HTML全文浏览量: 97
- PDF下载量: 22
出版历程
- 收稿日期: 2021-05-21
- 刊出日期: 2021-12-26

Reliability data analysis of EMU pantograph

XUE Kang^1,,
QI Jinping^{1, 2, 3,},
XU Ance⁴,
ZHOU Yahui¹,
LI Shaoxiong¹

1.
Mechatronics T&R Institute, Lanzhou Jiaotong University, Lanzhou　730070, China
2.
Gansu Province Engineering Technology Center for Information of Logistics & Transport Equipment, Lanzhou　730070, China
3.
Gansu Province Logistics and Transportation Equipment Industry Technology Center, Lanzhou　730070, China
4.
General Office, China Railway Lanzhou Group Co. Ltd., Lanzhou　730015, China

摘要

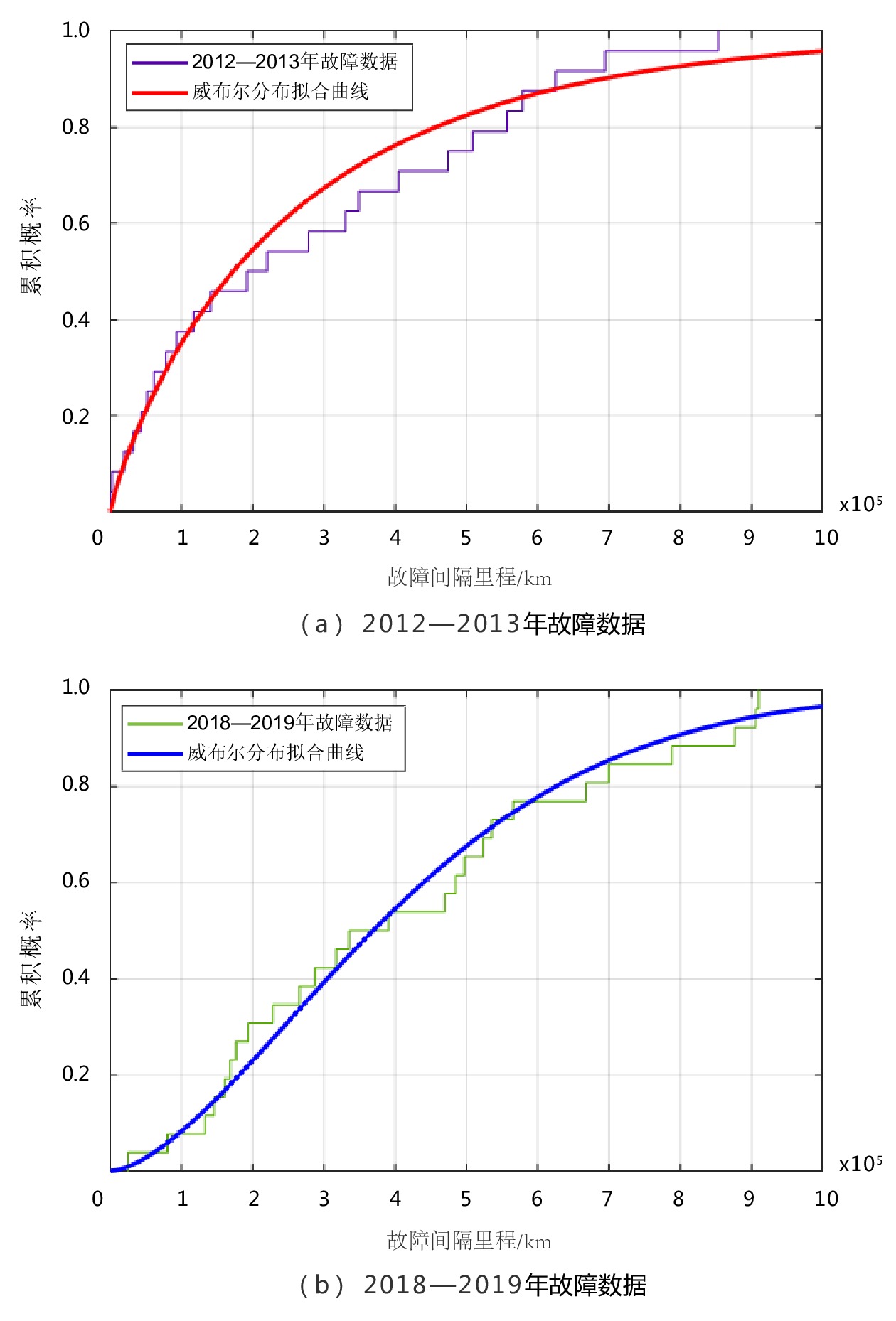
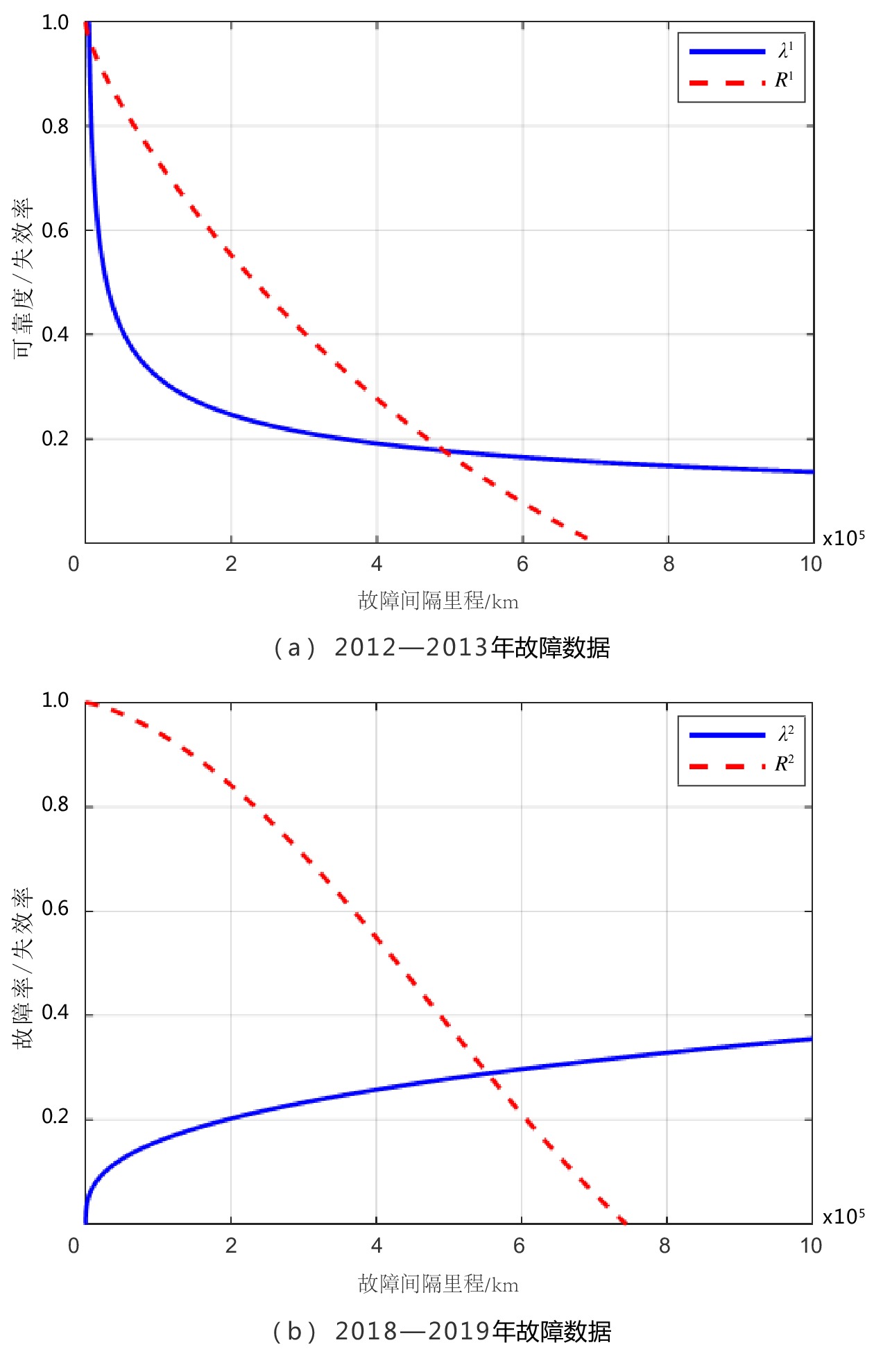
摘要: 为研究动车组受电弓在不同运营阶段的故障分布规律，文章以CRH3型动车组受电弓在不同运行阶段的两组故障数据为基础，运用最小二乘法分析故障数据的分布规律。计算结果表明，动车组受电弓故障数据服从威布尔分布；动车组受电弓在早期运营阶段故障率高，后期运营阶段故障率逐渐降低。本文的分析结果可以为不同运营阶段的动车组检修与故障预测提供理论依据。
- 受电弓 /
- 动车组 /
- 可靠性 /
- 威布尔分布 /
- 最小二乘法 /
- 数据分析
Abstract: In order to study the fault distribution law of EMU pantograph in different operation stages, based on the fault data of CRH3 EMU pantograph in two different operation stages, this paper analyzed the fault distribution law with the least square estimation method. The calculation results show that the pantograph fault data of EMU obey Weibull distribution, in the early operation stage, the failure rate is high and the failure occurs frequently, and the failure rate decreases gradually in the later operation stage. By using the method of reliability data analysis, the fault distribution in different stages can provide theoretical basis for the maintenance and fault prediction of EMU running on line at different times.
- pantograph /
- EMU /
- reliability /
- Weibull distribution /
- least square method /
- data analysis

HTML全文

图 1 可靠性数据分析的流程

下载: 全尺寸图片幻灯片

图 2 故障数据威布尔分布概率图

下载: 全尺寸图片幻灯片

图 3 累计概率密度曲线对比

下载: 全尺寸图片幻灯片

图 4 可靠度函数和失效率函数曲线

下载: 全尺寸图片幻灯片

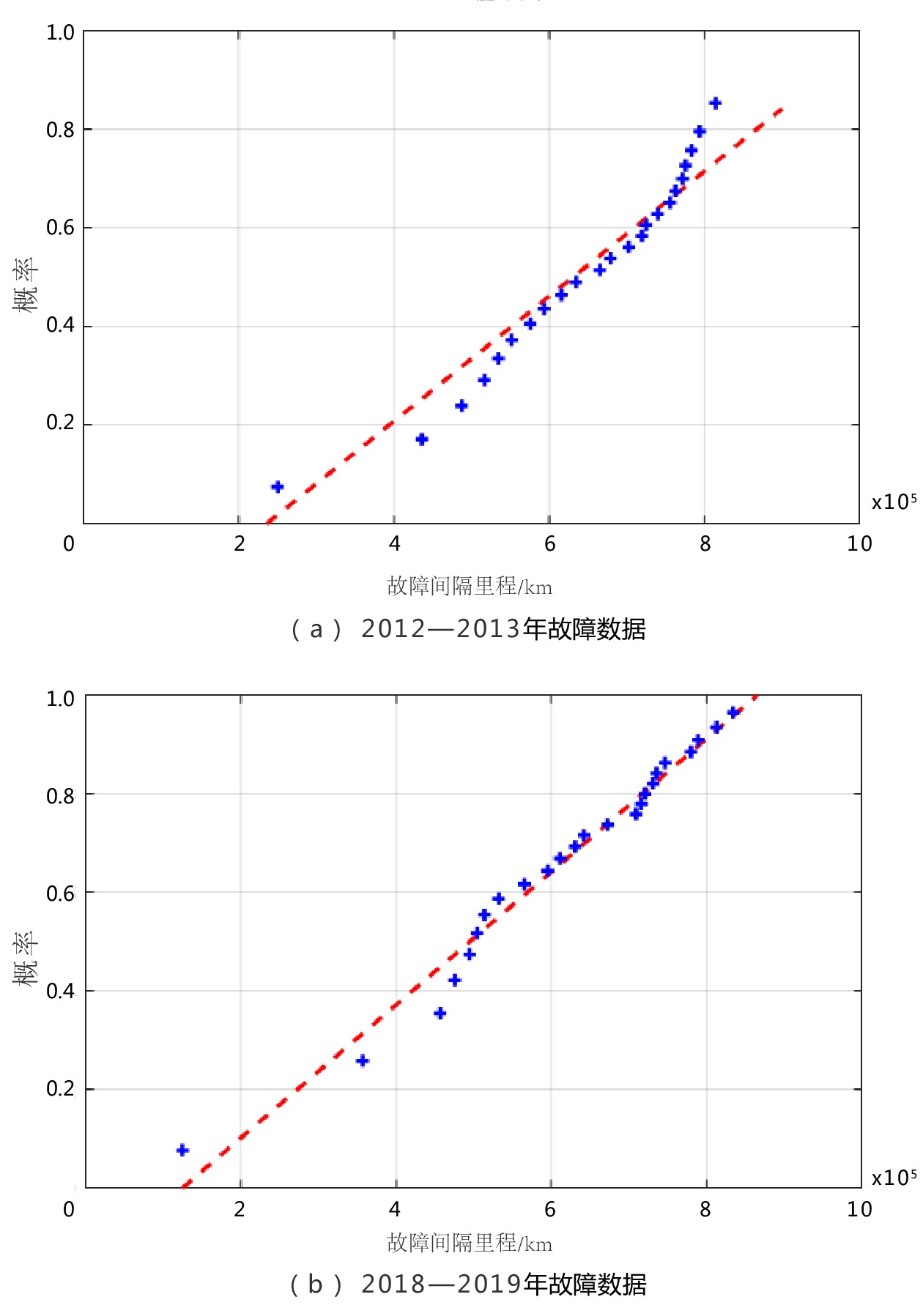
表 1 某高铁线受电弓故障数据及其中位秩（2012—2013年）

数据样本排序序号	t_i/ km	F(t_i)	数据样本排序序号	t_i/ km	F(t_i)
1	0.004 43×10⁵	0.028 7	13	2.202 03×10⁵	0.520 5
2	0.030 26×10⁵	0.069 7	14	2.785 99×10⁵	0.561 5
3	0.193 72×10⁵	0.110 7	15	3.302 06×10⁵	0.602 5
4	0.324 25×10⁵	0.151 6	16	3.488 73×10⁵	0.643 4
5	0.434 29×10⁵	0.192 6	17	4.049 05×10⁵	0.684 4
6	0.519 57×10⁵	0.233 6	18	4.745 61×10⁵	0.725 4
7	0.615 65×10⁵	0.274 6	19	5.087 07×10⁵	0.766 4
8	0.783 88×10⁵	0.315 6	20	5.57580×10⁵	0.807 4
9	0.935 82×10⁵	0.356 6	21	5.788 73×10⁵	0.848 4
10	1.170 36×10⁵	0.397 5	22	6.252 37×10⁵	0.889 3
11	1.413 05×10⁵	0.438 5	23	6.949 04×10⁵	0.930 3
12	1.921 94×10⁵	0.479 5	24	8.534 10×10⁵	0.971 3

下载: 导出CSV

表 2 某高铁线受电弓故障数据及其中位秩（2018—2019年）

数据样本排序序号	t_i/ km	F(t_i)	数据样本排序序号	t_i/ km	F(t_i)
1	0.252 58×10⁵	0.026 5	13	3.354 25×10⁵	0.481 1
2	0.805 68×10⁵	0.064 4	14	3.905 84×10⁵	0.518 9
3	1.328 62×10⁵	0.102 3	15	4.695 72×10⁵	0.556 8
4	1.459 80×10⁵	0.140 2	16	4.850 14×10⁵	0.594 7
5	1.605 62×10⁵	0.178 0	17	4.969 63×10⁵	0.632 6
6	1.686 80×10⁵	0.215 9	18	5.232 88×10⁵	0.670 5
7	1.767 50×10⁵	0.253 8	19	5.355 82×10⁵	0.708 3
8	1.936 87×10⁵	0.291 7	20	5.658 96×10⁵	0.746 2
9	2.285 69×10⁵	0.329 5	21	6.680 24×10⁵	0.784 1
10	2.656 92×10⁵	0.367 4	22	6.998 52×10⁵	0.822 0
11	2.875 04×10⁵	0.405 3	23	7.885 48×10⁵	0.859 8
12	3.168 57×10⁵	0.443 2	24	8.768 60×10⁵	0.897 7

下载: 导出CSV

表 3 某高铁线受电弓故障数据计算结果（2012—2013年）

数据样本排序序号	t_i/ km	x_i	y_i	数据样本排序序号	t_i/ km	x_i	y_i
1	0.004 43×10⁵	−5.419 4	−3.536 7	13	2.202 03×10⁵	0.789 4	−0.307 9
2	0.030 26×10⁵	−3.497 9	−2.628 1	14	2.785 99×10⁵	1.024 6	−0.193 2
3	0.193 72×10⁵	−1.641 3	−2.143 3	15	3.302 06×10⁵	1.194 5	−0.080 7
4	0.324 25×10⁵	−1.126 2	−1.805 2	16	3.488 73×10⁵	1.249 5	0.030 8
5	0.434 29×10⁵	−0.834 0	−1.541 9	17	4.049 05×10⁵	1.398 5	0.142 7
6	0.519 57×10⁵	−0.654 8	−1.324 0	18	4.745 61×10⁵	1.557 2	0.256 6
7	0.615 65×10⁵	−0.485 1	−1.136 3	19	5.087 07×10⁵	1.626 7	0.374 4
8	0.783 88×10⁵	−0.243 5	−0.969 8	20	5.57580×10⁵	1.718 4	0.499 0
9	0.935 82×10⁵	−0.066 3	−0.818 9	21	5.788 73×10⁵	1.755 9	0.634 6
10	1.170 36×10⁵	0.157 3	−0.679 8	22	6.252 37×10⁵	1.833 0	0.789 1
11	1.413 05×10⁵	0.345 8	−0.549 6	23	6.949 04×10⁵	1.938 6	0.979 8
12	1.921 94×10⁵	0.653 3	−0.426 2	24	8.534 10×10⁵	2.144 1	1.267 3
平均值	${ {\bar {x} }_1}$=0.225 8, ${ {\bar {y} }_1}$=−0.548 6

下载: 导出CSV

表 4 某高铁线受电弓故障数据计算结果（2018—2019年）

数据样本排序序号	t_i/ km	x_i	y_i	数据样本排序序号	t_i/ km	x_i	y_i
1	0.252 58×10⁵	−1.376 0	−3.616 6	13	3.354 25×10⁵	1.210 2	−0.421 6
2	0.805 68×10⁵	−0.216 1	−2.709 6	14	3.905 84×10⁵	1.362 5	−0.312 3
3	1.328 62×10⁵	0.284 1	−2.226 7	15	4.695 72×10⁵	1.546 7	−0.206 1
4	1.459 80×10⁵	0.378 3	−1.890 5	16	4.850 14×10⁵	1.579	−0.101 9
5	1.605 62×10⁵	0.473 5	−1.629 4	17	4.969 63×10⁵	1.603 3	0.001 2
6	1.686 80×10⁵	0.522 8	−1.413 7	18	5.232 88×10⁵	1.655 0	0.104 4
7	1.767 50×10⁵	0.569 6	−1.228 5	19	5.355 82×10⁵	1.678 2	0.208 8
8	1.936 87×10⁵	0.661 1	−1.064 7	20	5.658 96×10⁵	1.733 2	0.315 7
9	2.285 69×10⁵	0.826 7	−0.916 8	21	6.680 24×10⁵	1.899 2	0.427 2
10	2.656 92×10⁵	0.977 2	−0.781 0	22	6.998 52×10⁵	1.945 7	0.545 7
11	2.875 04×10⁵	1.056 1	−0.654 5	23	7.885 48×10⁵	2.065 0	0.675 5
12	3.168 57×10⁵	1.153 3	−0.535 3	24	8.768 60×10⁵	2.171 2	0.824 2
平均值	$ {\bar x_2} $=1.073 3, $ {\bar y_2} $=−0.691 9

下载: 导出CSV

参考文献(15)

[1]	孙有朝, 张永进. 可靠性原理与方法[M]. 北京: 科学出版社, 2016: 21-24.
[2]	刘诗佳. 动车组牵引系统故障统计分析 [J]. 铁道机车车辆,2013,33(5):80-85. DOI: 10.3969/j.issn.1008-7842.2013.05.20
[3]	王　韬. 基于贝叶斯网络的动车组牵引传动系统可靠性分析[D]. 成都: 西南交通大学, 2015.
[4]	崔秀国. CRH3型动车组电气系统可靠性研究[D]. 北京: 北京交通大学, 2013.
[5]	刘建强,崔秀国,孙帮成,等. CRH_3型动车组高压电器系统可靠性研究 [J]. 铁道学报,2013,35(6):22-27. DOI: 10.3969/j.issn.1001-8360.2013.06.004
[6]	董超跃. 基于动态贝叶斯网络的动车组牵引传动系统可靠性分析[D]. 北京: 北京交通大学, 2020.
[7]	徐　慧. 动态不确定环境下流程制造企业设备维修计划研究[D]. 上海: 上海交通大学, 2009.
[8]	李兴运,齐金平. 基于T-S模糊故障树的受电弓系统可靠性分析 [J]. 安全与环境学报,2018,18(1):33-38.
[9]	顾　瑛. 可靠性工程数学[M]. 北京: 电子工业出版社, 2004: 98-109.
[10]	赵　宇. 可靠性数据分析教程[M]. 北京: 北京航空航天大学出版社, 2009: 91-93.
[11]	金良琼. 两参数Weibull分布的参数估计[D]. 昆明: 云南大学, 2010.
[12]	伍建军,吴小明,谢周伟,等. 改进威布尔分布的矿冶零部件可靠性寿命预测研究 [J]. 机械科学与技术,2017,36(3):436-441.
[13]	王文岳,崔杰. 威布尔分布分析及其在产品寿命分析中的应用 [J]. 电子产品可靠性与环境试验,2019,37(5):16-26. DOI: 10.3969/j.issn.1672-5468.2019.05.003
[14]	王平永,刘宏昭,蒋喜,等. 高速铣削电主轴可靠性试验载荷谱的研究 [J]. 机械科学与技术,2013,32(2):279-284.
[15]	刘勇军,杨勇,范晋伟. 数控磨床液压系统可靠性建模与评估 [J]. 液压与气动,2016(9):16-20. DOI: 10.11832/j.issn.1000-4858.2016.09.003

施引文献(4)

期刊类型引用(3)

1.	田朋溢，石雯，陈彪，高攀，蒋成成，刘鹏. 无线分布式轨道车辆平稳性测试技术研究. 铁道机车车辆. 2024(06): 110-116 . 百度学术
2.	茅迿，高琦，梁师嵩. 城轨列车智能综合检测系统的研究与应用. 机车车辆工艺. 2023(01): 12-16 . 百度学术
3.	刘国联，陈根，张敏海. 基于CAN总线的铁路道岔监测系统设计. 南方农机. 2020(09): 217-219 . 百度学术