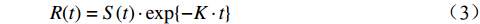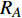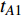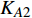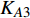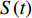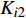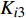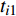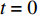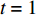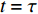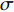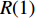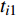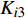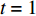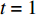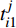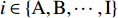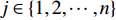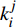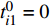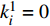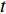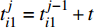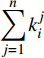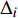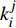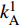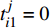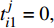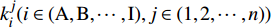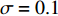Study on preventive maintenance strategy for switch machine components based on GO-FLOW method
-
摘要: 为解决目前转辙机因采用固定时间间隔的预防性维修导致的维修资源浪费及潜在人为失误造成的安全隐患,提出一种基于GO-FLOW方法的转辙机部件预防性维修策略;依据转辙机的组成结构和工作流程,建立转辙机GO-FLOW模型,在设备整体可靠性约束下,利用故障统计数据,计算在不同服役时间段内转辙机主要部件的可靠度,据此确定维修时间间隔变化的转辙机部件预防性维修方案,以实施针对性维修,更好地平衡维修经济性和安全性。Abstract: To deal with maintenance resources waste and potential human error hazards caused by fixed-interval preventive maintenance of switch machine components, a preventive maintenance strategy for switch machine components based on the GO-FLOW model is proposed. According to the composition, structure and working flow of the switch machine, a GO-FLOW model of the switch machine is constructed. Under the constraints of overall reliability of the switch machine, the degree of reliability of major components of the switch machine in different servicing periods can be quantitatively derived by use of failure statistics. Based on that, the preventive maintenance plan for switch machine components at variant maintenance intervals can be formulated so as to make more targeted maintenance, better balancing the economy and safety of maintenance.
-
作为轨道交通道岔转换的关键基础设备,转辙机能否安全、可靠地运行直接影响列车运行效率和行车安全[1]。转辙机部件繁多、结构复杂,且因安装在室外,易受各种因素影响,设备故障率较高。因此,制定切实可行的维修策略,保证转辙机的安全可靠尤为重要。
近年来,针对铁路信号设备特点,基于大数据和机器学习的故障诊断方法已取得一些成果[2-4]。刘大伟等人[5]提出建立铁路智能检测系统,实现设备故障提前预警,支持设备“故障修”向“状态修”转变;伏玉明等人[6]提出采用模糊综合评判法来评估转辙机的健康状况,综合考虑各种不确定影响因素,但并未进一步研究确定维修策略;王宁等人[7]采用隐半马尔可夫模型对设备进行状态识别和故障预测,需要积累大量历史数据,且仅适用于结构简单的设备;有学者提出健康管理技术,根据历史数据预测设备部件寿命,实现部件预防性维护[8-9]。这些方法仅对设备各个部件进行状态检测和预测,未考虑部件间复杂相关性。
目前,铁路转辙机部件的预防性维修采用较为粗放的固定维修间隔,由此带来的过度维修一方面造成维修资源浪费,同时还可能因潜在人为失误造成设备故障,引发安全事故。本文提出一种基于GO-FLOW方法的转辙机部件预防修策略,以转辙机整体可靠性为核心,对其部件可靠性变化进行定量分析,依据部件可靠度变化规律,确定合理的转辙机部件维修间隔。
1 GO-FLOW方法的原理介绍和分析步骤
20世纪80年代,日本学者Takeshi Matsuoka和Michiyuki Kobayashi在GO方法[10]的基础上提出GO-FLOW方法[11-12]。GO-FLOW方法是一种设备可靠性分析方法,采用图形演绎方式,根据设备内部信号流分析计算设备的失效概率。
1.1 GO-FLOW方法的特点
(1)GO-FLOW方法以成功为导向构建设备模型,主要用于分析状态随时间变化或具有复杂运行时序的系统的失效概率。
(2)GO-FLOW方法通过分析设备组成结构和工作原理,选择相应的操作符,将系统结构原理图转换为GO-FLOW模型图,基于操作符计算规则,进行设备可靠度的定量计算和定性分析,实现设备可靠性评价。
(3)GO-FLOW定义了14种操作符,构建的模型图与所研究设备的物理部件一一对应,可清晰地反映设备的组成结构,便于对照设备构造进行模型核查。
1.2 GO-FLOW方法的分析流程
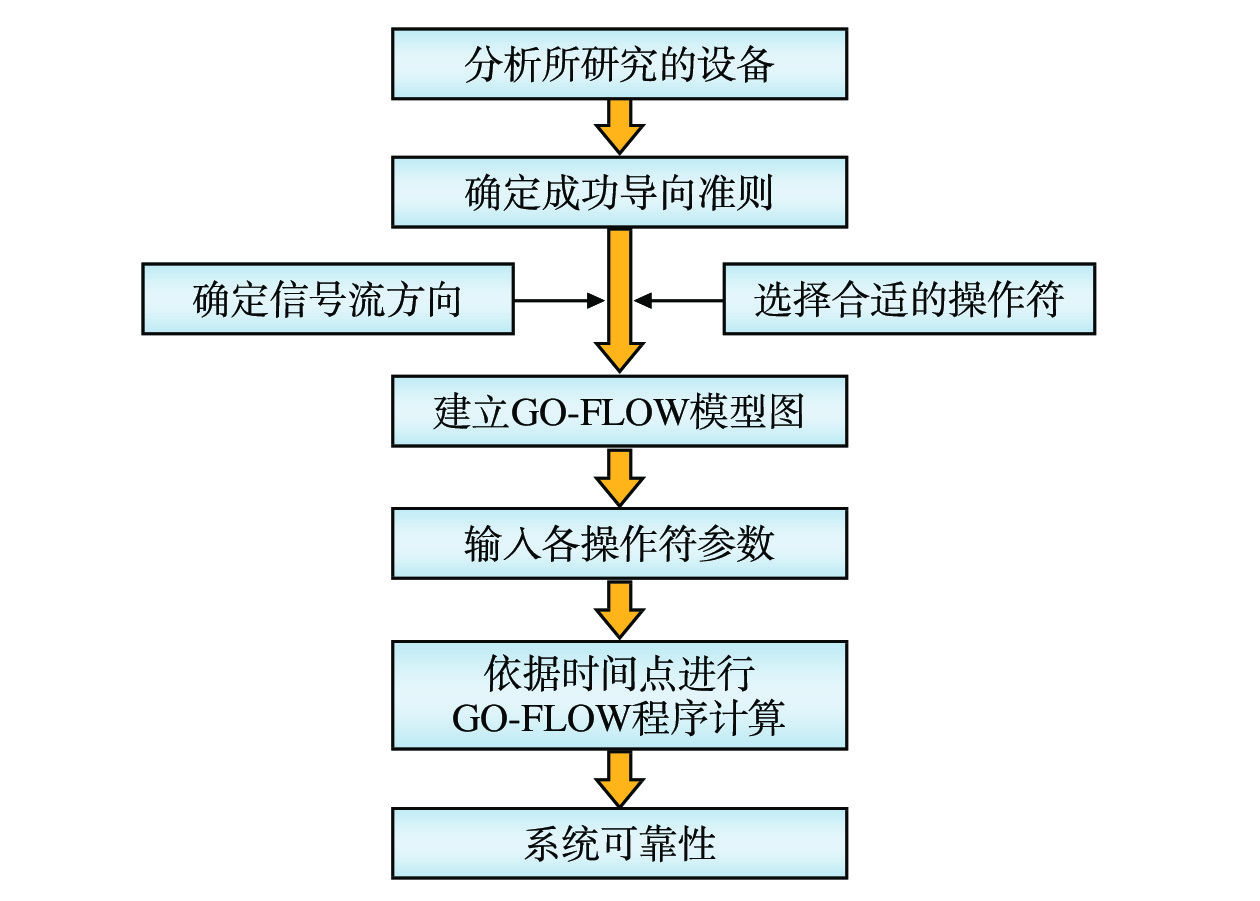
GO-FLOW模型主要包含3类要素:信号流、时间点和操作符。GO-FLOW方法的分析流程划分为GO-FLOW图构建和GO-FLOW程序运算2个阶段,如图1所示。
2 基于GO-FLOW方法的转辙机建模与可靠性分析
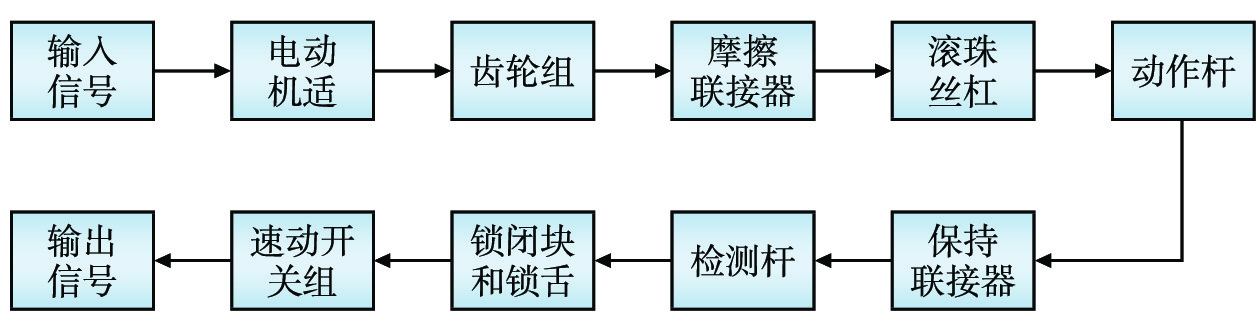
以S700K型转辙机为研究对象,系统主要由三相电动机、齿轮组、摩擦连接器、滚珠丝杆、保持连接器、动作杆、检测杆、锁闭块和锁舌及速动开关组9个部件组成[9],工作流程如图2所示;部件间联系紧密,任何部件发生故障均会造成转辙机无法正常工作。
以转辙机正常工作为成功导向准则,根据转辙机的工作流程建立GO-FLOW模型,信号流方向与转辙机工作流程一致,部件的可靠度用信号流强度表示。信号流强度越高,表明部件的可靠性越好,反之亦然。
2.1 GO-FLOW操作符选择和运算规则
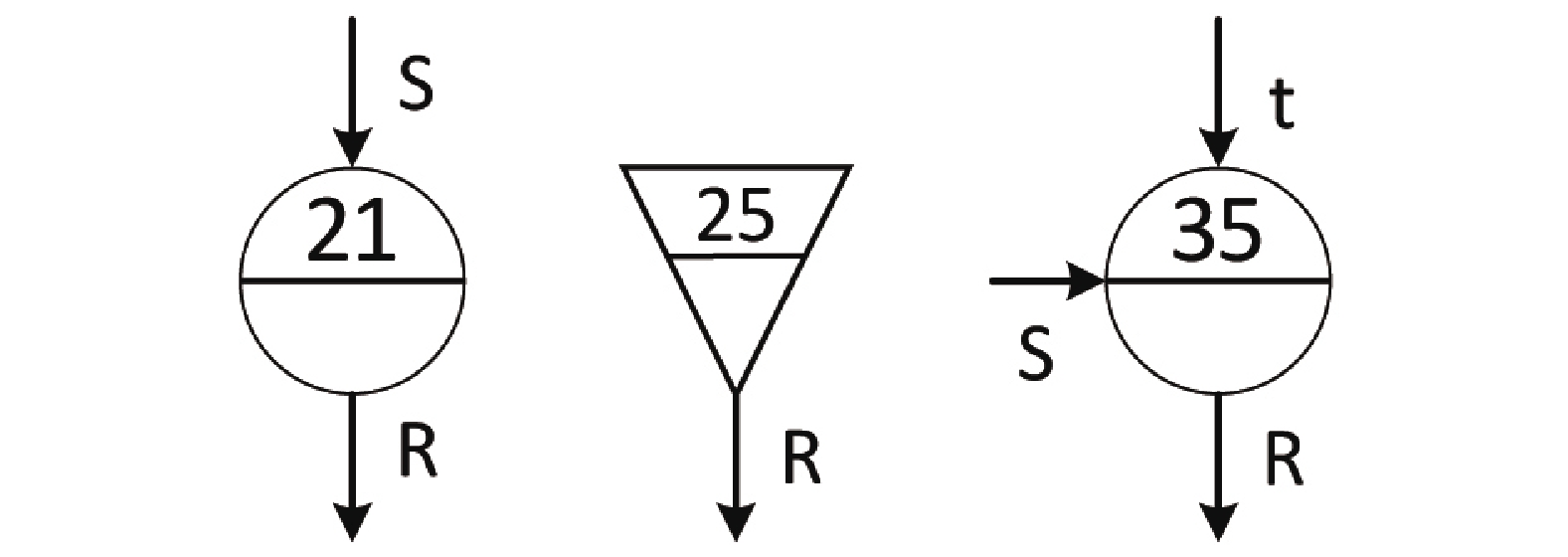
GO-FLOW定义了14种操作符,转辙机系统使用其中的3种类型操作符,如图3所示。基于转辙机的组成结构与工作原理,选择操作符21(两状态部件)代替转辙机的9个部件,选择操作符25(信号发生器)作为输入信号和输入时间点;鉴于部件在使用中可靠度会发生变化,选择操作符35(随时间失效的工作部件),模拟部件可靠性变化。
以S(t)、K、R(t)分别表示t时刻操作符的输入信号强度、正常工作概率和输出信号强度,则操作符的运算规则如下:
(1)两状态部件类型21操作符的输出信号强度为:
$$R(t) = S(t) \cdot K$$ (1) (2)信号发生器部件类型25操作符的输出信号强度为:
$$R(t) = K$$ (2) (3)对于随时间失效部件类型35,K表示部件的失效率,其输入信号t是时变单元,由于失效率随时间累加不断变大,所以输出信号强度会不断减小,其输出信号强度为:
$$R(t) = S(t) \cdot \exp \{ - K \cdot t\} $$ (3) 2.2 基于GO-FLOW操作符的部件等效模块设计示例
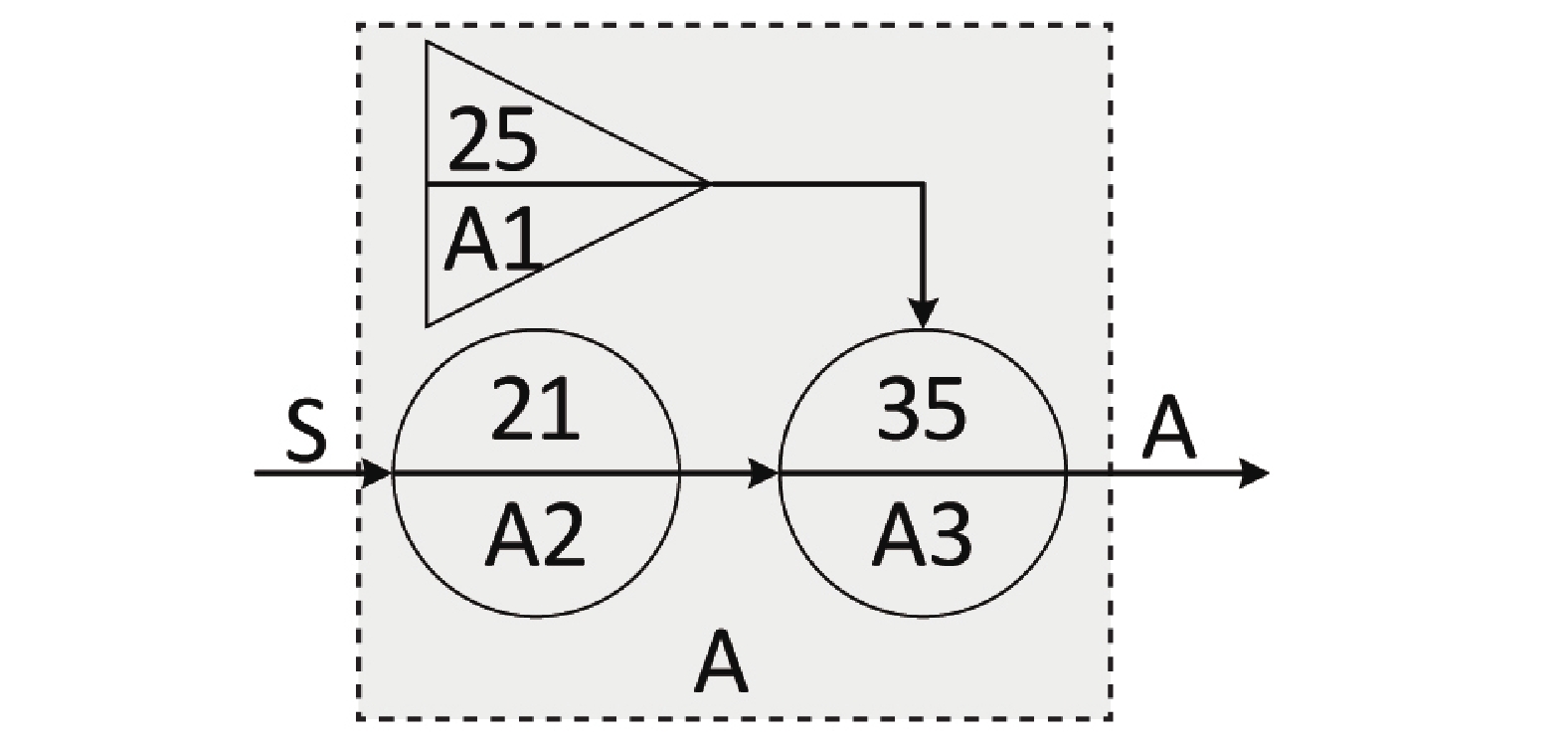
如图4所示,操作符A为转辙机电动机部件的等效模块,操作符中水平线上方表示符号类型,下方为对应编号,左边输入连接上一模块的输出,右边A表示当前模块的输出
${R_A}$ ;符号25表示电动机部件已工作时间${t_{A1}}$ ,符号21表示电动机部件能够正常工作的概率${K_{A2}}$ ,符号35表示部件的失效概率${K_{A3}}$ 。按式(1) ~ (3),该模块的输出信号强度为:$${R_A}(t) = S(t) \cdot {K_{A2}} \cdot \exp \{ - {t_{A1}} \cdot {K_{A3}}\} $$ (4) 2.3 基于GO-FLOW方法的转辙机建模
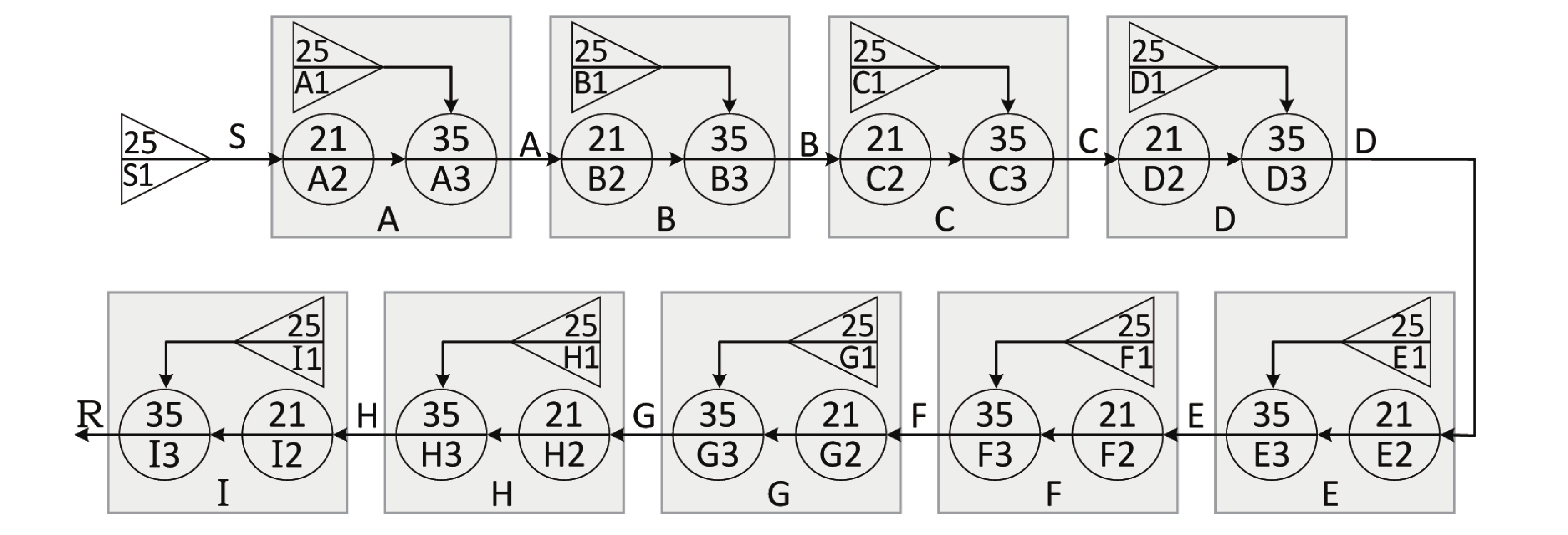
采用A、B、C、D、E、F、G、H和I分表代表转辙机的9个部件,编号S1表示输入设备,S为输入信号强度,R为转辙机的输出信号强度,构建如图5所示的GO-FLOW模型。由式(4)可推导出转辙机t时刻的输出信号强度为:
$$R(t) = S(t) \cdot \prod\limits_{i = A}^I {({K_{i2}} \cdot \exp \{ - {t_{i1}} \cdot {K_{i3}}\} } )$$ (5) 其中,
$S(t)$ 表示输入信号,${K_{i2}}$ 表示部件的正常工作概率;${K_{i3}}$ 表示部件随时间变化的失效概率;${t_{i1}}$ 表示部件的已工作时间。3 转辙机部件预防性维修策略
根据转辙机的使用步骤,定义3个时间点:时间点
$t = 0$ 为准备态,即转辙机还未投入使用;时间点$t = 1$ 为初始态,即转辙机正式投入使用中;时间点$t = \tau $ 为部件维修态,即转辙机处于不可靠状态,极可能发生故障。定义设备整体的可靠度下降
$\sigma $ 时,处于维修状态,则由式(5)可推导得出:$$ - \log (\frac{{R(1) - \sigma }}{{R(1)}}) = \sum\limits_{i = A}^I {({t_{i1}} + t) \cdot } {K_{i3}}$$ (6) 其中,
$R(1)$ 是设备刚投入使用时的可靠度;${t_{i1}}$ 为部件已工作的时间;${K_{i3}}$ 表示部件随时间变化的失效概率;$t$ 为待求的部件现阶段工作时间。当部件工作一段时间后,其正常工作的概率会降低,假设每个子模块的输入信号强度均为1(完全可靠),则由式(4)可以推导得到模块可靠度变化为:
$${\Delta _i} = {K_{i2}} - 1 \cdot {K_{i2}} \cdot \exp \{ - {t_{i1}} \cdot {K_{i3}}\} ,i \in \{ {\rm{A}},{\rm{B}},\cdots ,{\rm{I}}\} $$ (7) 3.1 部件维修间隔的计算流程
按时间点的划分,当
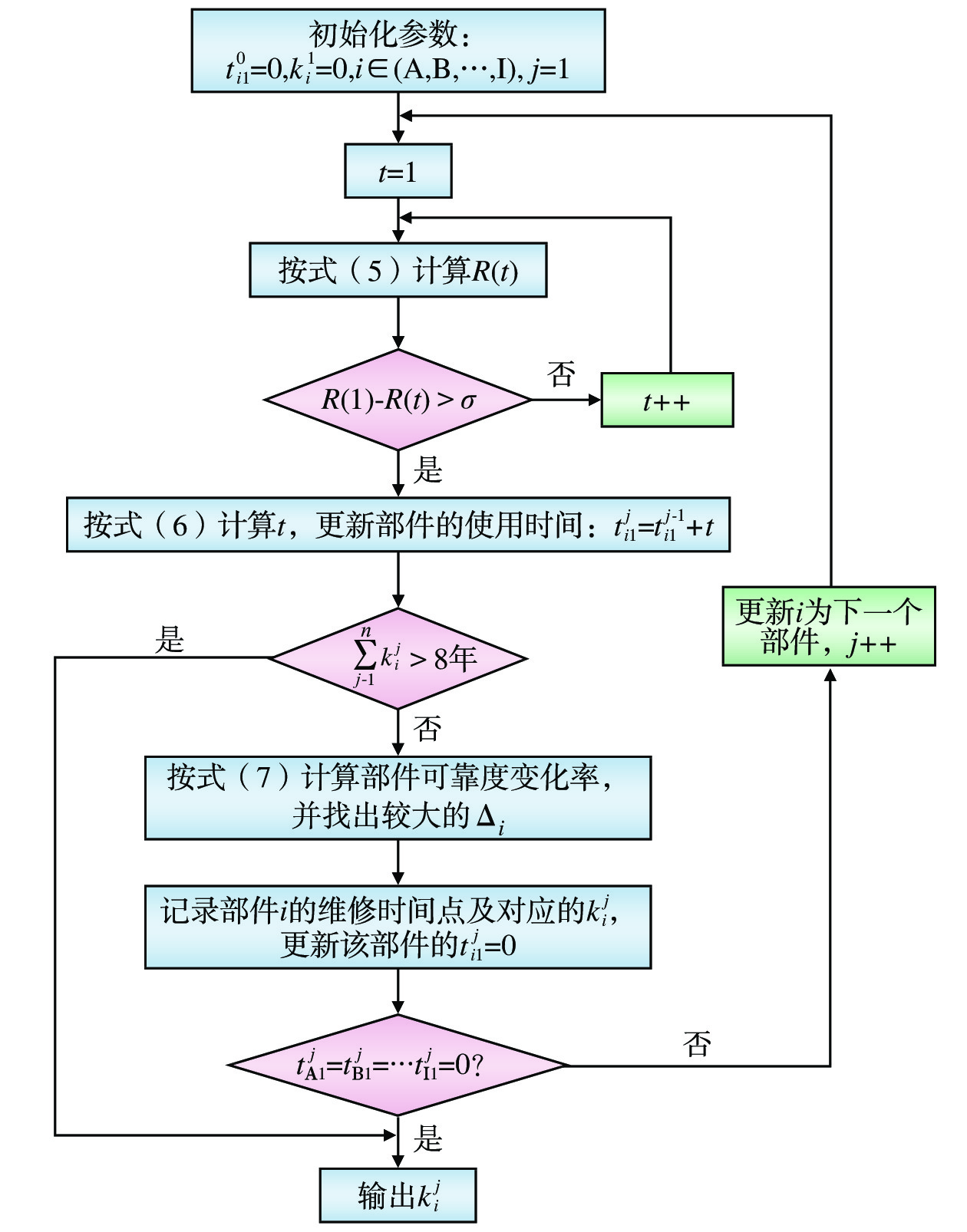
$t = 1$ 时表示转辙机正式投入使用,故令开始时间$t = 1$ 。转辙机正式使用后部件维修建立过程如图6所示,主要步骤如下。(1)参数初始化:
$t_{i1}^j$ 表示部件的历史工作时间,$i \in \{ {\rm{A}},{\rm{B}},\cdots ,{\rm{I}}\}$ 表示每个部件,$j \in \{ 1,2,\cdots ,n\}$ 用于区分时间点;$k_i^j$ 用来记录部件i的第j个维修时间点的时间;设置$ t_{i1}^0 = 0 $ ,$k_i^1 = 0$ ;(2)按式(5)计算部件的R(t),如R(1)–R(t)<σ,则更新时间t;否则按式(6)计算部件的工作时间
$t$ ,并更新部件i的使用时间$t_{i1}^j = t_{i1}^{j - 1} + t$ ;判断如果$\displaystyle\sum\limits_{j = 1}^n {k_i^j}$ 大于8年,则结束流程,否则转步骤(3);(3)按式(7)计算每个部件此时的可靠度变化率,找出变化率较大的部件
${\Delta _i}$ ,该部件即为维修部件;记录时间点和该部件的$k_i^j$ (如部件A,时间点1,记为$k_{\rm{A}}^1$ ),维修后令该部件的$t_{i1}^j = 0$ ;若多个部件的变化率相近,允许同时维修多个部件,维修后将多个部件的工作时间均设为0。判断是否出现$t_{i1}^j = 0, \;i \in \{ {\rm{A}}, {\rm{B}},\cdots , {\rm{I}}\}$ ,即所有的部件同时维修,如果是,则转步骤(4),否则更新i和j并转步骤 (2);(4)当所有部件都完成维修后,系统恢复到初始使用状态,此时不再执行流程,维修的部件和时间间隔按
$k_i^{{j}}(i \in ({\rm{A}},{\rm{B}},\cdots,{\rm{I}}),{{ }}j \in (1,2,\cdots ,n))$ 中存储的数据执行,流程结束。3.2 转辙机部件维修的时间间隔计算
假设转辙机的输入信号强度恒为1(完全可靠),设置阈值
$\sigma = 0.1$ (即设备可靠度下降10%,处于不安全状态,该值可视不同情形设置);参考相关文献[13],结合实际统计设置转辙机模型的参数见表1。表 1 转辙机模型参数编号 类型 单元名称 参数 S1 25 输入信号 $S = 1$ A2 21 电动机 ${K_{A2} } = {\rm{0} }{\rm{.999\,998\,151\,8} }$ A3 35 模拟失效单元 ${K_{A3} } = 5.544\,7 \times {10^{ {\rm{ - } }6} }$ B2 21 齿轮组 ${K_{B2} } = {\rm{0} }{\rm{.999\,994\,699\,9} }$ B3 35 模拟失效单元 ${K_{B3} } = 5.300\,1 \times {10^{ {\rm{ - } }6} }$ C2 21 摩擦联结器 ${K_{C2} } = {\rm{0} }{\rm{.999\,999\,565\,1} }$ C3 35 模拟失效单元 ${K_{C3} } = 0.652\,3 \times {10^{ {\rm{ - } }6} }$ D2 21 滚珠丝杠 ${K_{D2} } = {\rm{0} }{\rm{.999\,998\,532\,3} }$ D3 35 模拟失效单元 ${K_{D3} } = 1.467\,7 \times {10^{ {\rm{ - } }6} }$ E2 21 保持连接器 ${K_{E2} } = {\rm{0} }{\rm{.999\,999\,429\,2} }$ E3 35 模拟失效单元 ${K_{E3}} = 0.5708 \times {10^{{\rm{ - }}6}}$ F2 21 动作杆 ${K_{F2} } = {\rm{0} }{\rm{.999\,996\,901\,6} }$ F3 35 模拟失效单元 ${K_{F3} } = 1.549\,2 \times {10^{ {\rm{ - } }6} }$ G2 21 检测杆 ${K_{G2} } = {\rm{0} }{\rm{.999\,997\,227\,6} }$ G3 35 模拟失效单元 ${K_{G3} } = 1.386\,2 \times {10^{ {\rm{ - } }6} }$ H2 21 锁闭块和锁舌 ${K_{H2} } = {\rm{0} }{\rm{.999\,999\,633\,1} }$ H3 35 模拟失效单元 ${K_{H3} } = 0.733\,9 \times {10^{ {\rm{ - } }6} }$ I2 21 速动开关组 ${K_{I2} } = {\rm{0} }{\rm{.999\,999\,673\,8} }$ I3 35 模拟失效单元 ${K_{I3} } = 0.326\,2 \times {10^{ {\rm{ - } }6} }$ 注:${K_{i2}} $,${K_{i3}}$$(i \in \{ {\rm{A} },{\rm{B} }\cdots,{\rm{I} }\})$分别表示每小时部件正常工作的概率和部件的失效率。 采用Matlab软件完成计算,利用表1中的数据,按3.1小节中给出的相关算法计算转辙机投入使用后部件可靠度的变化和维修时间间隔,转辙机部件可靠度的变化见表2。
表 2 转辙机部件可靠度的变化设备服役
时间/h部件可靠度变化/% A B C D E F G H I t=6010 *3.28 *3.14 0.39 0.88 0.34 0.93 0.83 0.44 0.20 t=9760 *2.06 *1.97 0.64 1.42 0.56 1.50 1.34 0.71 0.32 t=12060 1.23 1.21 0.78 *1.75 0.67 *1.85 1.66 0.88 0.39 t=14160 *2.41 *2.31 0.92 0.31 0.81 0.33 1.94 1.03 0.46 t=16860 1.49 1.42 1.07 0.70 0.94 0.74 *2.26 1.20 0.54 t=18210 *2.22 *2.12 1.16 0.90 1.01 0.95 0.19 1.30 0.56 t=20710 *1.38 *1.32 *1.32 *1.26 *1.15 *1.33 0.53 *1.38 0.66 表2中,第1列为转辙机服役时间,表中带“*”号的数据项表示转辙机在某一服役时间段需要维修的部件。假设一个部件在维修后,其正常工作概率可恢复到初始态,即该部件已工作时间恢复为0。以第2行部件A的可靠度变化量“*2.06”为例,表示部件A再继续工作3 750 h(由9 760-6 010得到)后,其可靠度下降2.06%;同理,第2行部件C的可靠度变化量为0.64,表明部件C在工作9 760 h后,其可靠度下降0.64%;在第2行中,部件A和部件B的可靠度变化较大且相近,成为导致转辙机发生故障的主要因素,需对其进行维修。表2中的最后1行,当转辙机工作20 710 h后,除了部件G和I,其它部件的可靠度变化率相近,表明应对转辙机进行全面维修,将所有部件恢复至刚投入使用时的状态。转辙机的整体可靠度及其部件维修间隔见表3。
表 3 转辙机设备整体可靠度和部件维修间隔工作时间/h 设备整体可靠度 维修部件 t=1 0.999984 无 t=6010 (6010) 0.899984 电动机、齿轮组 t=9760 (3750) 0.899476 电动机、齿轮组 t=12060 (2300) 0.899788 滚珠丝杆、电动杆 t=14160 (2100) 0.899400 电动机、齿轮组 t=16860 (2700) 0.899745 检测杆 t=18210 (1350) 0.899479 电动机、齿轮组 t=20710 (2500) 0.899563 全面维修 表3中,第1列为转辙机的维修时间,括号内的时间是前后2次维修之间的时间间隔;第2列是设备整体可靠度;第3列是某一时刻需要维修的部件。当转辙机工作时间超过20 710 h时,由于所有部件均恢复到初始状态,后期的维修策略将依据表3循环执行。
由此可见,转辙机的维修时间间隔依次为:6 010 h,3750 h,2300 h,······,2500 h;维修时间间隔是一个变化量,且每次维修部件均不同,较好地解决了转辙机以往预防性维修中固定维修时间间隔所造成的“过维修”问题,可节约维修资源。采取上述分析方法,可知电动机和齿轮组维修相对频繁,通过实际故障统计分析,发现电动机和齿轮组故障率较高,从另一个方面也验证了本文方法的可行性。
4 结束语
转辙机在使用过程中其可靠性会不断下降,目前固定部件维修时间间隔的预防性维修方案在经济性和安全性方面都不太合理。本文根据转辙机系统的组成结构及工作流程,建立基于GO-FLOW方法的系统可靠性分析模型,对转辙机部件的可靠度进行定量分析;以转辙机整体可靠性为约束,分析识别可靠度显著降低的部件,据此制定维修时间间隔变化的转辙机部件预防性维修方案,以实施针对性维修,更好地平衡维修的经济性和安全性。
-
表 1 转辙机模型参数
编号 类型 单元名称 参数 S1 25 输入信号 $S = 1$ A2 21 电动机 ${K_{A2} } = {\rm{0} }{\rm{.999\,998\,151\,8} }$ A3 35 模拟失效单元 ${K_{A3} } = 5.544\,7 \times {10^{ {\rm{ - } }6} }$ B2 21 齿轮组 ${K_{B2} } = {\rm{0} }{\rm{.999\,994\,699\,9} }$ B3 35 模拟失效单元 ${K_{B3} } = 5.300\,1 \times {10^{ {\rm{ - } }6} }$ C2 21 摩擦联结器 ${K_{C2} } = {\rm{0} }{\rm{.999\,999\,565\,1} }$ C3 35 模拟失效单元 ${K_{C3} } = 0.652\,3 \times {10^{ {\rm{ - } }6} }$ D2 21 滚珠丝杠 ${K_{D2} } = {\rm{0} }{\rm{.999\,998\,532\,3} }$ D3 35 模拟失效单元 ${K_{D3} } = 1.467\,7 \times {10^{ {\rm{ - } }6} }$ E2 21 保持连接器 ${K_{E2} } = {\rm{0} }{\rm{.999\,999\,429\,2} }$ E3 35 模拟失效单元 ${K_{E3}} = 0.5708 \times {10^{{\rm{ - }}6}}$ F2 21 动作杆 ${K_{F2} } = {\rm{0} }{\rm{.999\,996\,901\,6} }$ F3 35 模拟失效单元 ${K_{F3} } = 1.549\,2 \times {10^{ {\rm{ - } }6} }$ G2 21 检测杆 ${K_{G2} } = {\rm{0} }{\rm{.999\,997\,227\,6} }$ G3 35 模拟失效单元 ${K_{G3} } = 1.386\,2 \times {10^{ {\rm{ - } }6} }$ H2 21 锁闭块和锁舌 ${K_{H2} } = {\rm{0} }{\rm{.999\,999\,633\,1} }$ H3 35 模拟失效单元 ${K_{H3} } = 0.733\,9 \times {10^{ {\rm{ - } }6} }$ I2 21 速动开关组 ${K_{I2} } = {\rm{0} }{\rm{.999\,999\,673\,8} }$ I3 35 模拟失效单元 ${K_{I3} } = 0.326\,2 \times {10^{ {\rm{ - } }6} }$ 注:${K_{i2}} $,${K_{i3}}$$(i \in \{ {\rm{A} },{\rm{B} }\cdots,{\rm{I} }\})$分别表示每小时部件正常工作的概率和部件的失效率。 表 2 转辙机部件可靠度的变化
设备服役
时间/h部件可靠度变化/% A B C D E F G H I t=6010 *3.28 *3.14 0.39 0.88 0.34 0.93 0.83 0.44 0.20 t=9760 *2.06 *1.97 0.64 1.42 0.56 1.50 1.34 0.71 0.32 t=12060 1.23 1.21 0.78 *1.75 0.67 *1.85 1.66 0.88 0.39 t=14160 *2.41 *2.31 0.92 0.31 0.81 0.33 1.94 1.03 0.46 t=16860 1.49 1.42 1.07 0.70 0.94 0.74 *2.26 1.20 0.54 t=18210 *2.22 *2.12 1.16 0.90 1.01 0.95 0.19 1.30 0.56 t=20710 *1.38 *1.32 *1.32 *1.26 *1.15 *1.33 0.53 *1.38 0.66 表 3 转辙机设备整体可靠度和部件维修间隔
工作时间/h 设备整体可靠度 维修部件 t=1 0.999984 无 t=6010 (6010) 0.899984 电动机、齿轮组 t=9760 (3750) 0.899476 电动机、齿轮组 t=12060 (2300) 0.899788 滚珠丝杆、电动杆 t=14160 (2100) 0.899400 电动机、齿轮组 t=16860 (2700) 0.899745 检测杆 t=18210 (1350) 0.899479 电动机、齿轮组 t=20710 (2500) 0.899563 全面维修 -
[1] 郭 进. 铁路信号基础 [M]. 北京: 中国铁道出版社, 2010. [2] 王瑞峰,陈旺斌. 基于灰色神经网络的S700K转辙机故障诊断方法研究 [J]. 铁道学报,2016,38(6):68-72. DOI: 10.3969/j.issn.1001-8360.2016.06.012 [3] Atamuradov V, Camci F, Baskan S, et al. Failure diagnostics for railway point machines using expert systems[C]//IEEE International Symposium on Diagnostics for Electric Machines, Power Electronics and Drives. IEEE, 2009: 1-5.
[4] Jonguk L, Heesu C, Daihee P, et al. Fault Detection and Diagnosis of Railway Point Machines by Sound Analysis: [J]. Sensors, 2016, 16(4): 549. DOI: 10.3390/s16040549
[5] 刘大为,郭 进,王小敏,等. 中国铁路信号系统智能监测技术 [J]. 西南交通大学学报,2014,49(5):904-912. DOI: 10.3969/j.issn.0258-2724.2014.05.025 [6] 伏玉明. 转辙机健康管理关键技术的研究[D]. 兰州: 兰州交通大学, 2017. [7] 王 宁,孙树栋,李淑敏,等. 基于DD-HSMM的设备运行状态识别与故障预测方法 [J]. 计算机集成制造系统,2012,18(8):1861-1868. [8] Ardakani H D, Lucas C, Siegel D, et al. PHM for railway system — A case study on the health assessment of the point machines[C]// Prognostics and Health Management. IEEE, 2012: 1-5.
[9] García F P, Pedregal D J, Roberts C. Time series methods applied to failure prediction and detection [J]. Reliability Engineering & System Safety, 2017, 95(6): 698-703.
[10] Shen Z, Yao W, Huang X. A quantification algorithm for a repairable system in the GO methodology [J]. Reliability Engineering & System Safety, 2003, 80(3): 293-298.
[11] Matsuoka T, Kobayashi M. GO-FLOW: A New Reliability Analysis Methodology [J]. Nuclear Science & Engineering, 1988, 98(1): 64-78.
[12] Matsuoka T. Improvement of the GO-FLOW Methodology [J]. Nuclear Engineering and Design, 1997, 175: 205-214. DOI: 10.1016/S0029-5493(97)00038-1
[13] 伏玉明,刘伯鸿,宋 爽. 基于模糊综合评判的转辙机健康评估研究 [J]. 铁道科学与工程学报,2017,14(5):1070-1076. DOI: 10.3969/j.issn.1672-7029.2017.05.026 -
期刊类型引用(0)
其他类型引用(2)




 下载:
下载: