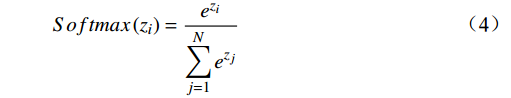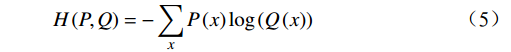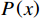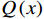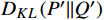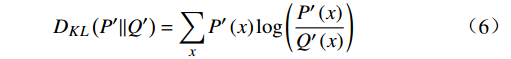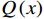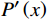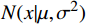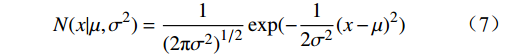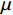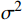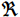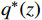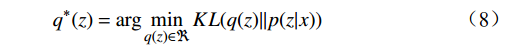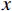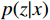Fault identification technology of platform door based on Bayesian neural network model
-
摘要:
针对城市轨道交通站台门系统面临的维护效率低下、运行数据缺失、严重依赖运营维护(简称:运维)人员技术水平等问题,提出一种基于贝叶斯神经网络模型的站台门故障识别方法。通过多维数据的采集和预处理,并采用Adam优化器对该模型进行训练和优化,在站台门运行状态实时监控的基础上,实现关键部件故障识别和智能运维。通过详细的测试与验证,结果表明,该模型在站台门故障模式识别方面具有优越的性能,可减少站台门系统平均维护时间,提升其可用性和可靠性,为城市轨道交通的安全运营提供强有力的支撑。
Abstract:This paper proposed a fault identification method of platform door based on Bayesian neural network model to address the problems faced by the platform door system of urban rail transit, such as low maintenance efficiency, missing operation data, and heavy reliance on the technical level of operation and maintenance personnel. The paper collected and preprocesses multidimensional data, and used Adam optimizer to train and optimize the model. Based on real-time monitoring of platform door operation status, it implemented key component fault identification and intelligent operation and maintenance. Through detailed testing and verification, the results show that the model has superior performance in platform door fault mode recognition, can reduce the average maintenance time of the platform door system, improve its availability and reliability, and provide strong support for the safe operation of urban rail transit.
-
随着旅客数量的增长和列车行车间隔的缩短,城市轨道交通行业面临的挑战日益加剧,加之大型体育、文化赛事等活动,以及航班或列车晚点,会引发旅客数量爆发式增长,使得车站客运组织和运营安全的压力更大。城市轨道交通站台门系统(简称:站台门系统)作为维护乘客安全和顺畅换乘的重要设施,一旦在运营期间发生故障且无法及时修复,会严重影响旅客乘降和列车运营,对车站客运组织极为不利。随着无人驾驶线路的增加和车站人员精减需求的进一步提升,对站台门系统的可靠性、可用性及可维护性的要求被推至新的高度。因此,确保站台门系统的持续高效运行,成为了轨道交通运营中的一个关键问题[1]。
目前,站台门系统的维护策略是定期检查与紧急修复相结合,这在站台门系统发生故障时可能会妨碍列车运输和车站处置[2]。此外,站台门系统的运行和故障状态通常是不透明的,这更增加了故障诊断和修复的难度,使得维护效率严重依赖于运营维护(简称:运维)人员的技术水平。因此,现有的维护模式制约了站台门系统的可维护性,迫切需要对其加以改进,以便适应快速发展的轨道交通需求[3]。
杨斌等人[4]提出了一种基于贝叶斯信念网络和神经网络自学习推理系统的混合技术,实现海量数据情况下的故障定位,用于电网故障诊断和安全评估;王新琪[5]提出了特征映射层逐渐拓宽且先验分布自适应更新的贝叶斯神经网络(BNN,Bayesian Neural Networks),并将其应用于数据的分类问题研究;胡城豪等人[6]在经典神经网络基础上引入不确定参数,提出基于高斯近似后验BNN的设备剩余寿命预测方法;王子涵等人[7]在基于BNN的机床热误差建模中,通过K-means聚类和相关系统法,选择温度敏感点,有效地测量点之间的多重共线性问题。由此可见,BNN已广泛应用于故障定位、设备管理等多个领域,但针对站台门系统智能运维的研究较少。
本文在充分了解站台门系统运行原理和运维场景的基础上,提出一种多维数据融合的故障识别方案,针对运维工作中的核心部件和关键故障进行深入分析,并基于BNN实现站台门系统的故障识别和智能运维,对提高维护效率、缓解运维压力、增强站台门系统可维护性方面具有重大意义。
1 数据分析与处理
1.1 关键要素分析
在城市轨道交通站台门系统中,滑动门作为乘客安全乘降的关键组成部分,其性能的稳定性和可靠性对城市轨道交通运营的安全与效率具有决定性影响。滑动门在门控单元的精确控制下,通过复杂的机械运动和电力调控,完成开闭动作,形成旅客乘降通道。因此,对滑动门运行状态的监控和维护显得尤为重要[8]。针对滑动门运行特性进行详细分析后,选取以下几项关键要素进行状态监测。
(1)运动曲线:反应滑动门的开闭动作是否遵循设定的轨迹和速度。稳定的行程和速度表明滑动门运行顺畅,没有意外停顿或过度加速的情况。
(2)振动振幅/震动:过度的磨损或异常情况会导致非正常震动,这可能因机械故障、传动部件性能不均匀或轨道上存在异物而引起。
(3)电压和电流:电流或电压的异常值可能表明电机过载、电路故障或其他组件问题。
(4)皮带松紧度:作为连接驱动电机和门体的关键组件,传动皮带的松紧度直接关系到门的开闭速度和运行稳定性。
1.2 数据采集和预处理
针对上述关键要素,为确保对滑动门的有效监控与维护,本文设计了一套综合性传感器监控方案。该方案通过使用位置速度传感器、震动传感器、电压电流传感器和皮带光栅传感器,实现对滑动门关键性能指标的实时监测。
为了有效处理这些多维数据,并为后续的数据分析和故障诊断奠定基础,数据预处理环节至关重要[9]。其目标是提高数据质量,确保分析和模型构建的高效与准确。这一过程主要包括数据清洗、缺失值填补和特征提取。
1.2.1 数据清洗
鉴于滑动门运行数据的连续性和周期性特点,本文采用拉依达准则法剔除异常数据。该方法基于正态分布假设,能有效剔除数据中的异常值,同时不会给系统带来过大的计算负担。通过此步骤,可以获得一个更准确、可靠的数据集。
假设监测数据序列X={x(1),x(2),···,x(n)},若某采样点x(i)满足公式:
$$ \left\{\begin{array}{l}\left|x\left(i\right)-\bar{x}\right| > 3\sigma \\ \bar{x}=\frac{1}{n}\displaystyle\sum _{j=1}^{n}x\left(j\right)\\ \sigma =\sqrt{\frac{1}{n}\displaystyle\sum _{j=1}^{n}{\left(x\left(j\right)-\bar{x}\right)}^{2}}\end{array}\right. $$ (1) 则将其判定为异常数据,将其从数据集中剔除。
式(1)中,
$ x\left(i\right) $ 为需要剔除的异常值;$ \bar{x} $ 为算数平均值;$ \sigma $ 为序列的标准差。1.2.2 数据填充
本文选取的关键要素在正常运行状态下均表现出连续变化的趋势,且传感器在数据采集过程中未遭遇严重的数据缺失问题。然而,在同时处理多个传感器数据时,由于传感器数据在时间上可能存在不一致,因此,需要采用时序差值方法来解决这一问题。为了平衡数据精度和处理效率,本文采用简单高效的近邻插补法来补充缺失值,即
$$ \hat{x}\left(r\right)=\frac{1}{2}\left(x\left(r-1\right)+x\left(r+1\right)\right) $$ (2) 式(2)中,
$ x\left(r-1\right) $ 和$ x\left(r+1\right) $ 分别表示缺失数据前面和后面的数据;$ \hat{x}\left(r\right) $ 表示填充的数据。1.2.3 特征提取
本文所述的特征提取包含时域特征和频域特征。时域特征直接通过传感器提取数据后进行预处理,频域特征则通过傅里叶变换获取。
$$ F(\omega)=\int f(t) e^{-j \omega t} {\mathrm{d}} t F(\omega)=\int f(t) e^{-j \omega t} {\mathrm{d}} t $$ (3) 式(3)中,F(ω)为频域中的复数函数;f (t)为时域中的函数;ω为频率。
在上述分析的基础上,本文提取的时域和频域关键指标,如表1所示。
表 1 特征提取的要素监测要素 时域特征 频域特征 运动曲线 速度、加速度、运行时间,
分阶段运动轨迹周期性运动产生的主频率及其谐波 振动振幅 最大振幅、平均振幅以及
振动信号的时变特性振动的主导频率及其变化 电压和电流 电压和电流的波形变化、
瞬时峰值和平均值电机的电源频率和谐波成分 皮带松紧度 振动幅度 抖动频率 2 BNN模型
2.1 BNN模型构建
2.1.1 BNN模型结构
在设计针对特定任务的BNN模型时,输入层、隐藏层和输出层的结构设计至关重要,它们直接影响BNN模型的性能和效率。BNN如图1所示。
(1)输入层的设计直接根据特征选择和降维的结果来定。在本文中,通过预处理后得到表1中时域和频域共计8个关键特征,故输入层由8个节点组成。每个节点代表一个关键特征,确保BNN模型能够接收并处理所有的关键信息。
(2)BNN模型结构包含两个隐藏层,用来捕捉复杂的非线性关系,同时避免其过于复杂,以免引起过拟合。考虑到实时性和计算资源的限制,每个隐藏层均设计为30个节点。这种设计在提升BNN模型学习能力的同时,能够很好地控制计算复杂性和资源消耗,实现优化和效率之间的平衡。对于隐藏层,本文使用ReLU(Rectified Linear Unit)激活函数。ReLU函数在训练BNN模型时有助于避免梯度消失的问题,且计算效率较高。
(3)输出层的设计需要根据具体任务的需求来定。对于多分类问题,如本案例中的故障类型分类,输出层的节点数应与故障类型的数量一致。因此,考虑到本案例中有9种典型的故障类型,包括电机故障、皮带磨损、吊挂轮磨损、导轨磨损、电压异常、电流异常、开门遇阻、关门遇阻、电磁锁故障,外加正常状态,输出层设计为10个节点。每个节点对应一种故障类型(或正常)。BNN模型的输出旨在为故障维护策略的制定提供明确的依据。对于输出层,鉴于本研究的输出是故障类别信息,选用Softmax函数来输出属于各个类别的概率。其公式为
$$ Softmax\left({z}_{i}\right)=\frac{{e}^{{z}_{i}}}{\displaystyle\sum _{j=1}^{N}{e}^{{z}_{j}}} $$ (4) 式(4)中,N表示类别的个数;zi表示第i个类别的原始分数。
综上所述,BNN模型的设计旨在通过合理的层级结构和节点设置,有效捕捉输入特征与输出类别之间的复杂关系,同时考虑效率和资源的限制,以期达到最优的性能表现。
2.1.2 损失函数
BNN模型的损失函数是一个组合损失,由两部分组成,分别是与数据似然相关的损失和KL散度。本文中与数据似然相关的损失采用交叉熵损失函数
${H}\left(P,Q\right) $ 表示,其计算公式为$$ {H}\left(P,Q\right)=-\sum_{x}P\left(x\right)\mathrm{log}\left(Q\left(x\right)\right) $$ (5) 式(5)中,
$ P\left(x\right) $ 是真实标签分布的概率;$ Q\left(x\right) $ 是模型预测分布的概率。KL散度
${D}_{KL}\left(P'||Q'\right) $ 的计算公式为$$ {D}_{KL}\left(P'||Q'\right)=\sum_{x}P'\left(x\right)\mathrm{log}\left(\frac{P'\left(x\right)}{Q'\left(x\right)}\right) $$ (6) 式(6)中,
$ Q\left(x\right) $ 表示BNN模型的后验分布;$ P'\left(x\right) $ 表示先验分布。本文选用的损失函数结合了数据的拟合度和参数的先验知识,通过这种损失函数构建的BNN模型,在学习数据的同时,保持了对模型参数不确定性的量化,使得模型在解释数据时更加稳健,能够表现出较传统神经网络更好的泛化性能。
2.2 BNN模型处理
2.2.1 引入先验分布
在BNN模型中,为每个权重和偏置项指定一个先验分布是整合先验知识和观测数据的基础[10]。鉴于不同厂商的数据存在一定差异,为保持站台门系统的通用性,采用无信息先验方法来引入先验分布。
本文选用高斯分布作为先验,因为高斯分布的数学性质,尤其是其共轭先验的特性,使得后验分布的分析或近似计算变得更为简单。此外,高斯分布在中心极限定理的背景下,为许多自然和社会过程提供了良好的近似。先验分布
$N(x|\mu ,{\sigma ^2}) $ 的计算公式为$$ N(x|\mu ,{\sigma ^2}) = \frac{1}{{{{(2{\text{π}} {\sigma ^2})}^{1/2}}}}\exp ( - \frac{1}{{2{\sigma ^2}}}{\left( {x - \mu } \right)^2}) $$ (7) 式(7)中,
$ \mu $ 是均值;$ {\sigma ^2} $ 是方差。先验分布的参数(均值和方差)均设为0,这样可以保持BNN模型的中立性。零均值高斯分布允许参数在零点附近自由变化,保留了模型的灵活性。
2.2.2 后验分布的推断
在BNN模型中,直接计算后验分布通常是不可行的,本文使用变分推断(VI,Variational Inference)作为近似方法。其主要步骤是:
(1)假定一个近似分布族
$ \Re $ ,作为隐变量分布的候选集;(2)从分布族中选择最优的分布
${q^*}(z) $ ,最小化KL散度,计算公式为$$ {q^*}(z) = \arg \mathop {\min }\limits_{q(z) \in \Re } {{KL}}(q(z)||p(z|x)) $$ (8) 式(8)中,
$x$ 是观测变量;$z$ 是隐变量;$p(z|x)$ 是后验概率密度。(3)通过最优的分布q*(z)来近似后验。
变分推断的核心是选择一个变分族,并找到最优的变分参数(均值和方差),使得变分分布尽可能接近真实的后验分布[10]。本文选择均值参数化的高斯分布族。通过这种方式,变分推断可以在保持参数不确定性的同时拟合数据,从而为BNN提供一个强大的学习框架。
2.3 训练策略
为了有效地训练BNN模型以应对站台门故障识别中的挑战,需要采取特定的训练策略和算法。在优化过程中,BNN的权重不是单个固定值,而是分布的参数,这意味着每次前向传播时,BNN的权重都是从这些分布中采样得到。本文采用TensorFlow框架下的Adam优化器对BNN模型进行训练和优化。
为提高内存利用率和训练速度,采用迷你批次方式进行BNN模型训练,并选择合适的批次大小,以平衡训练效率和收敛速度。使用动态学习率调整策略,在训练开始时快速进步。在训练后期,通过细化BNN模型参数来提高其精确度。
通过采取上述训练策略和算法,可以有效地训练BNN模型,为站台门的智能运维提供准确的预测,同时,量化预测的不确定性,为决策提供重要信息。
3 测试与验证
3.1 数据处理
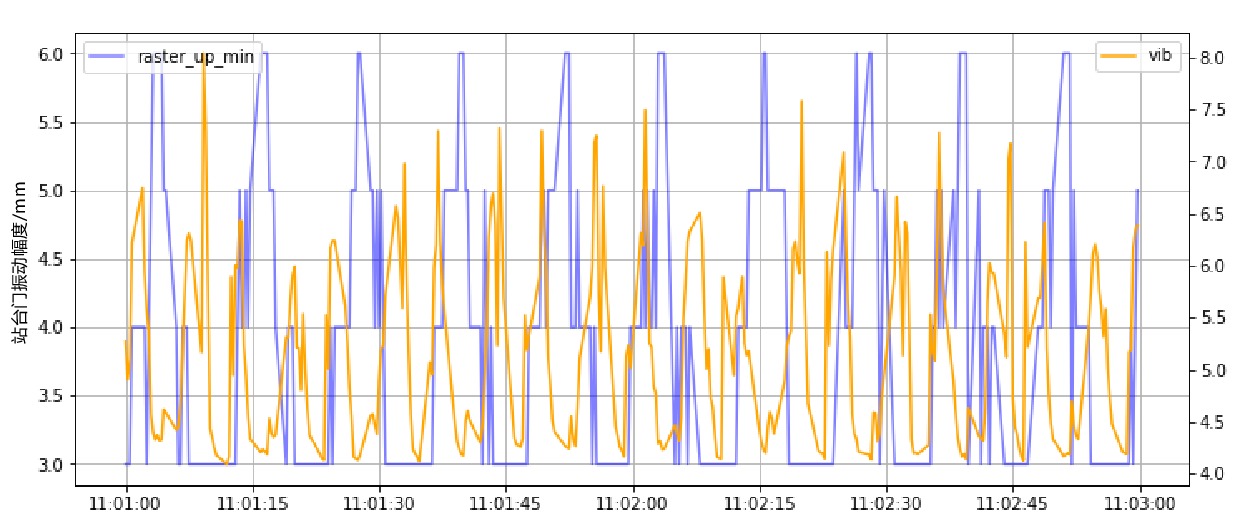
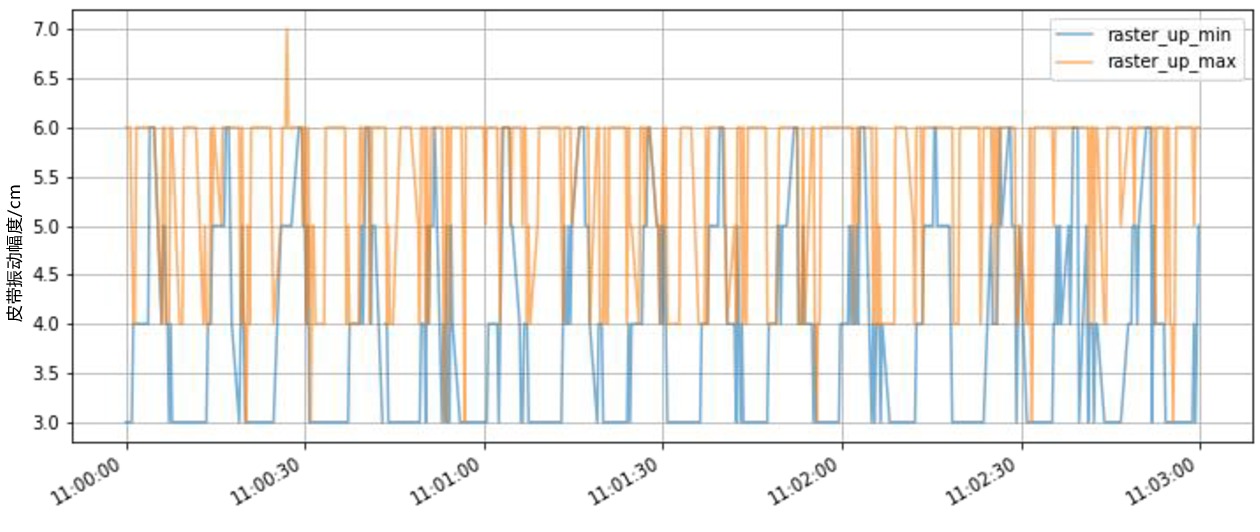
从站台门样机采集运行数据,对光栅、震动等数据进行采集和处理,经过预处理后的信号如图2、图3所示。站台门测定的振动信号与皮带光栅信号的数据采集符合预期;站台门开关动作的振动信号具有较高的重复性,幅值及频域特征稳定,作为BNN的输入是非常合适的数据。
3.2 实验结果与分析
在工程样机中模拟生成故障,并结合实际运行过程中产生的故障数据,作为数据集,共计
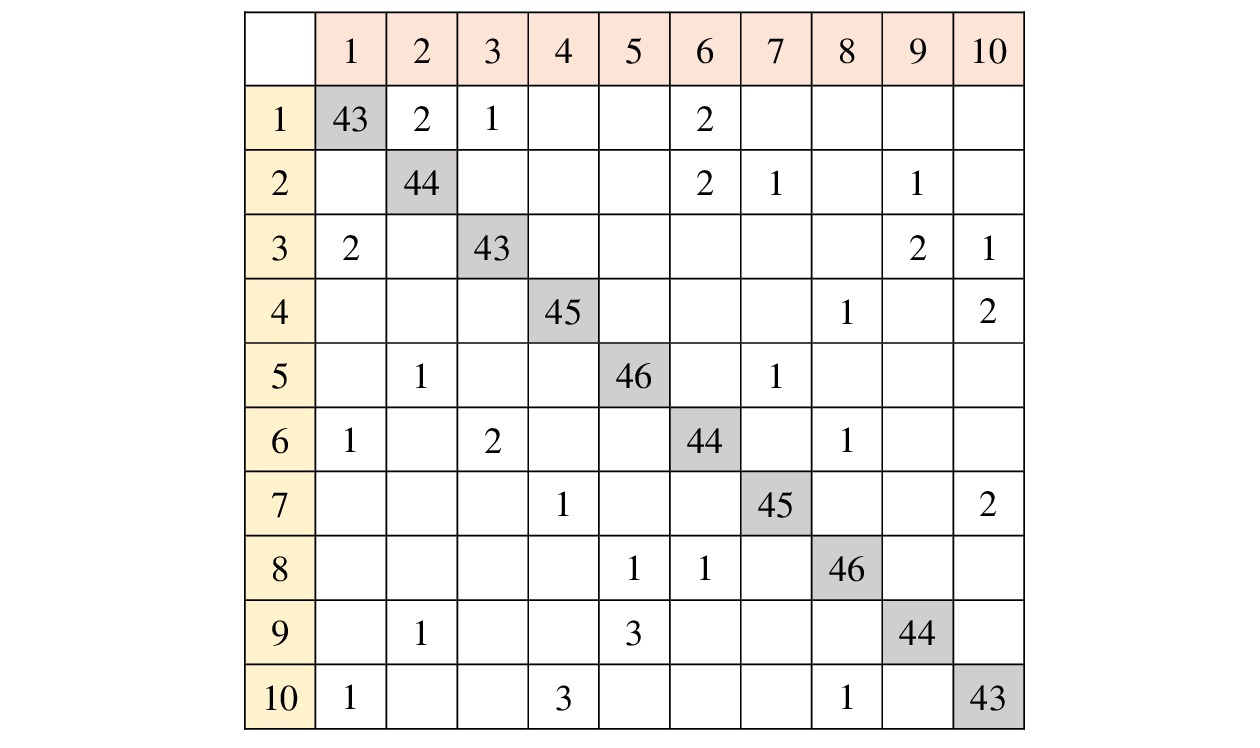
1600 条数据,涵盖9种典型的故障(输出类型编号为1—9)和正常状态(输出类型编号10),将其中70%作为训练集,30%作为验证集。验证集的混淆矩阵如图4所示,BNN模型在每个类别上的预测结果与实际结果的一致性,由此可知,各组数据的分类准确性较高,BNN模型能够准确地识别和区分不同的故障类型和正常状态,验证了本文所述方法的适用性和准确性。
BNN模型的性能指标,如表2所示,包括准确率、召回率和F1分数。它们从不同角度反映了BNN模型对数据的分类能力。由表2可知,BNN模型的准确率、灵敏度和F1分数均表现出优越的性能,这意味着BNN模型不仅能够准确识别出大多数样本类别,而且在检测故障时也具有高召回率,同时保持了良好的精确率。
表 2 验证结果统计指标 准确率 召回率 F1分数 1 0.896 0.919 0.921 2 0.917 0.926 0.922 3 0.896 0.904 0.893 4 0.938 0.962 0.956 5 0.958 0.972 0.969 6 0.917 0.935 0.943 7 0.938 0.967 0.962 8 0.958 0.973 0.971 9 0.917 0.899 0.906 10 0.896 0.887 0.902 4 结束语
本文针对站台门系统智能运维的主要问题,提出一种基于贝叶斯神经网络的站台门故障识别方法,采用Adam优化器对BNN模型进行训练和优化,通过不断增加的训练数据和迭代训练的优化,提升了BNN模型的识别能力和适应性。在未来的研究中,将进一步优化BNN模型结构,增强其在复杂环境中的鲁棒性,并探索更高效的故障分类算法,以期在实际应用中实现更加精准和高效的故障检测和维护决策。
-
表 1 特征提取的要素
监测要素 时域特征 频域特征 运动曲线 速度、加速度、运行时间,
分阶段运动轨迹周期性运动产生的主频率及其谐波 振动振幅 最大振幅、平均振幅以及
振动信号的时变特性振动的主导频率及其变化 电压和电流 电压和电流的波形变化、
瞬时峰值和平均值电机的电源频率和谐波成分 皮带松紧度 振动幅度 抖动频率 表 2 验证结果统计
指标 准确率 召回率 F1分数 1 0.896 0.919 0.921 2 0.917 0.926 0.922 3 0.896 0.904 0.893 4 0.938 0.962 0.956 5 0.958 0.972 0.969 6 0.917 0.935 0.943 7 0.938 0.967 0.962 8 0.958 0.973 0.971 9 0.917 0.899 0.906 10 0.896 0.887 0.902 -
[1] 赵 晗,尹恩华,李伯男. 城市轨道交通站台门智能运维系统研究[J]. 都市快轨交通,2023,36(2):156-161. DOI: 10.3969/j.issn.1672-6073.2023.02.019 [2] 李 帅,左艳芳,郭顺利,等. 基于全自动运行的智能站台门控制系统研究[J]. 铁路计算机应用,2020,29(11):44-48. DOI: 10.3969/j.issn.1005-8451.2020.11.012 [3] 王金峰,丁树森,刘思缈. 地铁站台门设备智能运维系统探索[J]. 科技创新导报,2022,19(23):85-88. [4] 杨 斌,胡真瑜,赵 静,等. 基于混合贝叶斯神经网络的电网故障处置诊断研究[J]. 自动化技术与应用,2023,42(12):168-171. [5] 王新琪. 基于宽度贝叶斯神经网络的分类方法研究[D]. 大连:大连理工大学,2019. [6] 胡城豪,胡昌华. 考虑多种贝叶斯神经网络分布形式组合的设备剩余寿命预测方法[J]. 电光与控制,2021,28(11):79-83. DOI: 10.3969/j.issn.1671-637x.2021.11.017. [7] 王子涵,杨秀芝,段现银,等. 基于贝叶斯神经网络的机床热误差建模[J]. 制造技术与机床,2022(1):141-145. [8] 张银龙. 市域铁路智慧站台门系统关键技术[J]. 中国机械工程,2021,32(4):475-480. DOI: 10.3969/j.issn.1004-132X.2021.04.013. [9] 胡城豪,胡昌华,司小胜. 基于贝叶斯神经网络的设备剩余寿命预测方法[J]. 火箭军工程大学学报(自然科学版),2021(2):9. [10] 陈冠恒,郭子瑜,梅广旭,等. 一种针对关系不确定性的贝叶斯异质图神经网络[J]. 计算机学报,2023,46(3):552-567. DOI: 10.11897/SP.J.1016.2023.00552




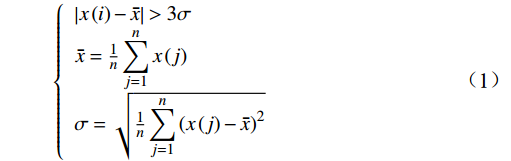
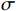
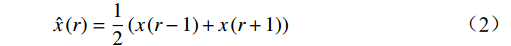
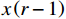
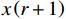
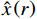
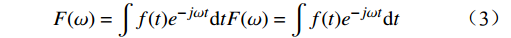
 下载:
下载: