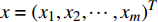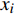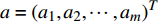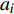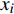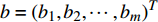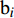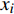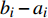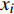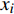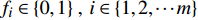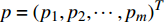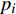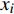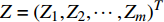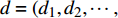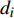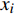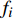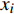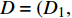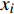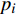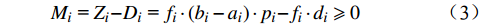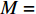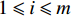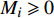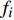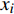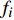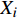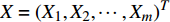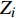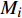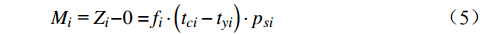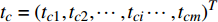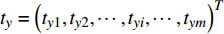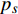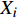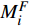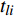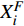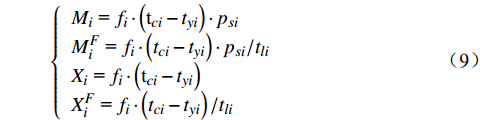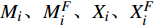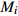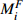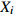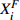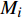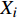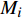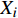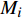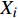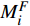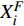自2016年至2021年，全国铁路货运总发送量由333 186万t增长至477 372万t，全国铁路货运总周转量由23 792.26亿t·km增长至33 238.00亿t·km^[1]。铁路物流在迅速发展的同时，对物流效率的追求也越来越迫切。铁路货运票据电子化的实施，将纸质单据替换为电子单据，显著增强了铁路货运系统间的数据交互能力 ^[2]。2021年实施的中国铁路95306货运电子商务系统网站升级项目，显著增强了客户服务能力，提高了货物承运效率。作为铁路物流的起点和终点，货运车站（简称：车站）担负着货物承运、到达、交付等物流的核心环节，其物流效率得到了越来越多的关注。

影响铁路货运效率的因素较多，主要包括：货车利用效率、场站规划、技术设备条件、信息化水平、运输组织水平、运输模式及超限车的开行等^[3-4]。对现有的3000多个车站全部进行改造来实现效率升级既不现实也无必要，且各车站限制物流效率的原因各不相同，改造后效率提升情况不同，能承受的升级代价也不同^[5]。

针对车站物流效率优化的研究主要包括两个方面：（1）研究建立大型物流园或对主要铁路物流节点车站进行完全改造升级，实现铁路物流整体效率的提升，包括物流园选址研究、车站布局研究等^[4-6]，但无法解决大多数现有货运站的效率优化问题；（2）进行包括装卸设备在内的设备自动化升级，仓储的自动化、智能化升级，作业信息化改造和配套的业务流程优化^[7-8]。但上述优化方法大都需要人工来分析确定是否需升级，或全部进行升级改造，很难按照每个车站现有情况安排优化方法^[9-11]。本文基于车站物流作业流程，构建了多指标车站物流效率优化模型，并通过实际数据展示优化过程，为车站物流效率优化提供技术支持。

1   一般货运车站物流作业流程

一般货运车站物流作业流程如图1所示。车站主要作业流程是以车辆到达和货物进站开始，以车辆出发和货物出门验放结束^[2,7]。主要又可分为车辆进站卸车过程和车辆装车出站过程。（1）车辆进站卸车过程为：车辆到站后，若是空车则不需进行卸车操作，若为重车，则通过接车对位或路企交接执行入线，待车辆卸前检查等操作后开始卸车；货物卸完后，即可通过通知取车和路企交接执行出线；出线后，车辆即等待下一次装货；货物则执行交付作业，最后出门验放，货物出站。（2）车辆装车出站过程与车辆进站卸货过程相反，货物在车站装车后离开车站；专用线作业与货场作业流程稍有不同，但主要是作业环节先后顺序和作业地点区别。

图  1  车站物流作业流程

下载: 全尺寸图片 幻灯片

2   物流效率多指标优化方法

2.1   物流效率优化分析

车站物流各作业环节的效率优化有多种方式：（1）可通过增加足够长度和数量的作业线来提高货场自动化水平和存储空间、优化作业线布局、添加自动化的装卸设备来实现；（2）可通过调整作业人员、升级信息系统、提前编制计划等方式来实现；（3）可通过添加高清货检设备，加快货检、车检速度，减少排队等待时间等方式来实现。

车站物流效率受限于基础设施、车站组织作业能力和车站网络调度能力。无论优化基础设施，还是优化组织作业或布局，都是具体实施方法。为了构建更有效、更具有指导性的优化方法，可通过构建车站物流效率优化指标来分析和表述效率优化，并通过指标来比较、分析车站物流效率瓶颈，进而通过现有的优化方式来对车站进行效率优化。

2.2   物流效率优化构成及限制

为评估车站物流效率优化效果，寻找可优化的车站及其物流单元，可通过对车站物流效率优化构成及限制进行分析，从而获取多个优化指标。在此基础上，综合分析多个优化指标，构建车站物流效率优化方法。

设某车站C有m个物流单元，则其车站流程可表示为向量${{x}} = {\left( {{x_1},{x_2}, \cdots ,{x_m}} \right)^T}$ ，其中，${{{x}}_i}$ 表示该车站第i个物流单元。

设优化前效率指标为a，则${{a}} = {\left( {{a_1},{a_2}, \cdots ,{a_m}} \right)^T}$ ，其中，${{{a}}_i}$ 表示物流单元${{{x}}_i}$优化前的效率情况。设优化后效率指标为b，则${{b}} = {\left( {{b_1},{b_2}, \cdots ,{b_m}} \right)^T}$，其中，${{\text{b}}_i}$ 表示物流单元${{{x}}_i}$优化后的效率情况。则可用${b_{{i}}} - {a_i}$表示物流单元 ${{{x}}_i}$ 优化前后效率的增益情况。

对车站C的m个物流单元，可将车站物流单元${{{x}}_i}$ 是否优化表示为${f_i} \in \{ 0,1\} \;,\;i \in \{ 1,2, \cdots m\}$ 。设车站平均作业量指标为p，则有${{p}} = {\left( {{p_1},{p_2}, \cdots ,{p_m}} \right)^T}$，其中，${{{p}}_i}$ 表示物流单元${{{x}}_i}$平均作业量。由此可得到车站物流效率优化效益增益${{Z}} = {\left( {{{{Z}}_1},{{{Z}}_2}, \cdots ,{{{Z}}_m}} \right)^T}$，其中

设效率优化限制条件为d，则有${{d}} = ( {d_1},{d_2}, \cdots , {d_m} )^T$ ，其中${{{d}}_i}$ 表示物流单元 ${{{x}}_i}$ 效率优化限制。故有，在${f_i}$ 情况下，车站 ${{{x}}_i}$ 物流单元优化限制为${{D}} = ( {{{D}}_1}, {{{D}}_2}, \cdots ,{{{D}}_m})^T$，其中

由此可得，车站 ${{{x}}_i}$ 物流单元在作业量 ${{{p}}_i}$ 条件下，物流效率优化需满足条件

车站C物流效率优化需满足条件为：对于${{M}} = {\left( {{{{M}}_1},{{{M}}_2}, \cdots ,{{{M}}_m}} \right)^T}$，任意${{1 \leqslant i \leqslant m}}$，存在${{{M}}_i} \geqslant 0$。

对于车站优化，其物流效率越低，优化的需求就越高，故可得到在${f_i}$ 情况下，车站 ${{{x}}_i}$ 物流单元实际效率优化情况

当${f_i}$为1时，${{{X}}_i}$越大，则越需要优化。车站C实际效率优化情况为${{X}} = {\left( {{{{X}}_1},{{{X}}_2}, \cdots ,{{{X}}_m}} \right)^T}$。

2.3   物流效率多指标优化模型构建

车站作业流程中划分的多个顺序连接的模块对单个车辆整个作业流程效率的贡献无法通过增加单位时间内完成的物流单元作业次数来实现，而需要通过缩减物流单元的作业时长来实现。因此，本文采用时间来表征物流效率。

车站平均作业量指标可用单位时间内总作业吨数或单位时间内总作业车数来表示。由于两指标间有较强的相关性，本文采用单位时间内总作业车数来表示。为分析各作业阶段间效率的区别，本文采用平均作业时长作为物流效率衡量指标，不同车站相同作业阶段，平均作业时间越长则效率越低，平均作业时间越短则效率越高。车站在某物流单元优化后的物流效率衡量指标，采用全路该物流单元最优时间来表示。

由于效率优化限制条件暂时无法取得，本文采用设定参数d=0，并通过计算${{{Z}}_i}$较大值来评价是否可以优化。将以上参数代入公式（3）可得指标 $ {M_i} $ 为

其中，${{{t}}_c} = {\left( {{t_{c1}},{t_{c2}}, \cdots ,{t_{c{{i}}}} \cdots ,{t_{cm}}} \right)^T}$为车站各物流单元平均作业时间，${{{t}}_y} = {\left( {{t_{y1}},{t_{y2}}, \cdots ,{t_{y{{i}}}}, \cdots ,{t_{ym}}} \right)^T}$是全路各物流单元最优时间，作业量$ {p_s} $表示平均每日作业车数。

将以上参数代入公式（4），可得指标$ {X_i} $为

为比较相同车站不同物流单元的作业效率，需要对物流效率衡量指标进行处理，以全路该物流单元平均作业时间作为参照，采用 （车站该物流单元平均作业时间–全路该物流单元平均作业时间）/全路该物流单元平均作业时间，作为效率衡量指标，若小于0表示效率高于平均水平的程度，大于0表示效率低于平均水平的程度。如此，相同车站的不同模块间可进行比较。

由此，将以上参数与新的物流单元作业效率指标代入公式（3）可得新的指标$ M_i^F $为

其中，$ {t_{li}} $为该物流单元全路平均作业时间。

同理，将以上参数与新的物流单元作业效率指标代入公式（4），可得指标${{X}}_i^F$为

故可得多指标车站物流优化模型为

其中，指标${M}_{i}、{M}_{i}^{F}、{X}_{i}、{X}_{i}^{F}$值越大，表示该车站物流单元优化后效率指标提升越大。

3   模型应用

本文采用2021年1月至3月某些车站的物流数据，以a车站、b车站等代替实际车站名称，根据多指标车站物流效率优化模型计算得到的各指标结果如表1、表2、表3、表4所示。

表  1  指标$ {M_i} $计算结果

车站	提报到受理	入线到开装	开装到装完	装完到出线	出线到 出站	到站到 入线	入线到开卸	开卸到卸完>	卸完到出线
a车站	70485	40073	90999	15535	457270	126663	6932	18907	3103
b车站	310546	94230	88798	93707	357961	135745	18812	24108	25636
c车站	330844	5869	69088	2730	255887	109734	11026	23391	926
d车站	253426	274686	32798	3129	327069	104783	1797	12987	1636
e车站	74660	2706	14678	10	124484	73608	2287	14710	38160
f车站	781861	52744	106701	33370	836578	181920	25552	92176	24892
g车站	35872	406	3246	3909	246798	172433	10527	31261	9592
h车站	627	12	108	12	1706	39063	241	4523	726

下载: 导出CSV 

| 显示表格

表  2  指标$ M_i^F $计算结果

车站	提报到受理	入线到开装	开装到装完	装完到出线	出线到出站	到站到入线	入线到开卸	开卸到卸完	卸完到出线
a车站	126	266	628	422	648	199	109	115	17
b车站	556	626	613	2546	508	213	295	147	144
c车站	592	39	477	74	363	172	173	143	5
d车站	454	1824	226	85	464	165	28	79	9
e车站	134	18	101	0	177	116	36	90	215
f车站	1400	350	736	907	1186	286	401	562	140
g车站	64	3	22	106	350	271	165	191	54
h车站	1	0	1	0	2	61	4	28	4

下载: 导出CSV 

| 显示表格

表  3  指标$ {X_i} $计算结果

车站	提报到受理	入线到开装	开装到装完	装完到出线	出线到出站	到站到入线	入线到开卸	开卸到卸完	卸完到出线
a车站	78	44	101	17	507	1110	61	166	27
b车站	202	61	58	61	233	335	46	59	63
c车站	600	11	125	5	464	567	57	121	5
d车站	868	941	112	11	1121	728	12	90	11
e车站	622	23	122	0	1037	601	19	120	312
f车站	884	60	121	38	946	400	56	202	55
g车站	514	6	47	56	3536	971	59	176	54
h车站	508	10	87	10	1383	1643	10	190	31

下载: 导出CSV 

| 显示表格

表  4  指标$ X_i^F $计算结果

车站	提报到受理	入线到开装	开装到装完	装完到出线	出线到出站	到站到入线	入线到开卸	开卸到卸完	卸完到出线
a车站	0.14	0.29	0.70	0.47	0.72	1.74	0.95	1.01	0.15
b车站	0.36	0.41	0.40	1.65	0.33	0.53	0.73	0.36	0.36
c车站	1.07	0.07	0.86	0.13	0.66	0.89	0.89	0.74	0.03
d车站	1.55	6.25	0.78	0.29	1.59	1.14	0.20	0.55	0.06
e车站	1.11	0.15	0.84	0.00	1.47	0.94	0.29	0.73	1.76
f车站	1.58	0.40	0.83	1.03	1.34	0.63	0.88	1.24	0.31
g车站	0.92	0.04	0.32	1.52	5.01	1.53	0.93	1.07	0.30
h车站	0.91	0.06	0.60	0.27	1.96	2.58	0.16	1.16	0.17

下载: 导出CSV 

| 显示表格

由表1可知， f车站的$ {M_i} $指标计算结果均比较大，故最需要优化物流效率，其次是a车站、b车站、c车站和d车站。

由表2可知， b车站“装完到出线”物流单元、d车站“入线到开装”物流单元、f车站“提报到受理”物流单元和“出线到出站”物流单元应最需要优化物流效率。

由表3可知， g车站和h车站 $ {X_i} $ 指标计算结果数值较大，故最需要优化物流效率。

由表4可知， d车站“入线到开装”物流单元需要优化，其次是g车站“出线到出站”物流单元。

综合各指标可知，如果要对车站整体物流效率进行优化，需要比较指标 $ {M_i} $和指标 $ {X_i} $，应首先优化f车站，其次是b车站。a车站虽然 $ {M_i} $ 指标结果较高，但 $ {X_i} $ 指标数据较低，排在b车站后优化，e车站无优化必要。如果只优化车站某个流程，需要比较指标 $ M_i^F $ 和指标 $ X_i^F $，应首先优化b车站“装完到出线”物流单元和d车站“入线到开装”物流单元。

4   结束语

本文通过分析铁路物流作业流程，构建了多指标车站物流效率优化模型，为车站优化提供了更准确的优化目标。基于多个车站的实际作业数据，通过模型得到了各车站的优化目标，为车站物流效率优化提供了一种新的思考方式。

下一步将更详细地分析车站物流作业流程，包括集装箱运输与整车运输作业流程、不同品类货物装卸和存储、专用线和货场作业区别等，以提供更加准确有效的优化方式。