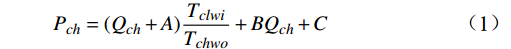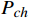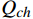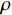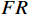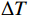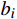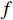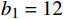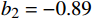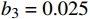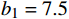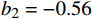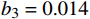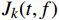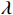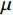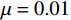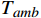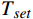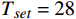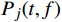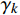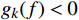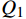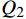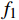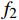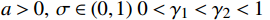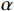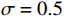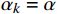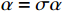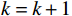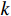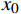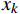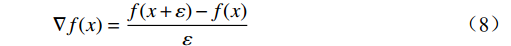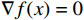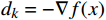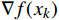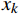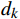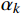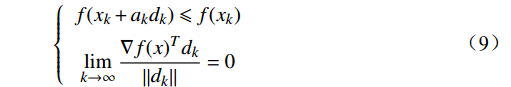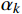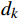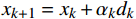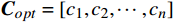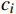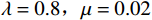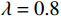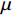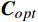基于最优控制方法的地铁车站节能控制模型

曹扬阳; 王晓峻; 魏青松; 徐宏伟; 梁奕

doi:10.3969/j.issn.1005-8451.2025.06.15

基于最优控制方法的地铁车站节能控制模型

1.
南京南瑞工业控制技术有限公司　系统研发二部，210031　南京
2.
南京佳强久视科技有限公司，210000　南京

基金项目:

国家重点研发计划（2021YFB2401300）；江苏省产业前瞻与关键核心技术重点项目（BE2020081-1）

详细信息

作者简介:
曹扬阳，助理工程师

王晓峻，高级工程师

中图分类号: U231.4 : TP39
计量
- 文章访问数: 22
- HTML全文浏览量: 4
- PDF下载量: 5
出版历程
- 收稿日期: 2025-03-02
- 网络出版日期: 2025-06-25
- 刊出日期: 2025-06-24

Energy saving control model for metro stations based on optimal control method

1.
System R & D Department II, NARI Industrial Control Technology Co. Ltd., Nanjing　210031, China
2.
Jiaqiang Jiushi Technology Co. Ltd., Nanjing　210000, China

摘要

摘要:
针对地铁车站空调通风系统能耗高的问题，文章提出一种基于最优控制方法的地铁车站节能控制模型。利用厦门市某地铁车站能源管理系统的实测数据，借助瞬时系统模拟（TRNSYS，Transient System Simulation）程序构建该地铁车站的空调通风系统能耗模型，在此基础上，提出一种基于多目标优化问题的最优控制方法，即：建立该优化问题的能耗代价函数和温度误差代价函数，采用最速下降法得到最优解，再利用粒子群算法验证解的全局最优性。试验结果表明，相比定频控制和粒子群（PSO，Particle Swarm Optimization）改进的PID（Proportional-Integral-Derivative）控制，最优控制方法提高了响应速度，减少了调节时间，降低了稳态误差，节能率分别提高了38.68%和8.1%。通过优化计算全局最优控制量矩阵，完成空调通风系统冷负荷动态匹配，实现了降低温度偏差和空调通风系统总能耗的目标，提高了节能控制系统的控制性能与经济性。
- 最优控制 /
- 多目标优化 /
- 地铁车站 /
- 空调通风系统 /
- 节能控制模型
Abstract:
This paper proposed an energy-saving control model for metro stations based on optimal control method to address the issue of high energy consumption in air conditioning and ventilation systems, used the measured data of the energy management system of a metro station in Xiamen City, and constructed the energy consumption model of the air conditioning and ventilation system of the metro station with the help of the Transient System Simulation (TRNSYS) Program. Based on this, the paper proposed an optimal control method based on multi-objective optimization problem, that was, establishing the energy consumption cost function and temperature error cost function of the optimization problem, using the steepest descent method to obtain the optimal solution, and then using particle swarm optimization algorithm to verify the global optimality of the solution. The experimental results show that compared with fixed frequency control and Particle Swarm Optimization (PSO) improved PID (Proportional Integral Derivative) control, the optimal control method improves response speed, reduces adjustment time, lowers steady-state error, and increases energy savings by 38.68% and 8.1%, respectively. This paper optimizes the calculation of the global optimal control matrix to achieve dynamic matching of cooling load in the air conditioning and ventilation system, achieving the goal of reducing temperature deviation and total energy consumption of the air conditioning and ventilation system, and improving the control performance and economy of the energy-saving control system.
- optimal control /
- multi-objective optimisation /
- metro station /
- air conditioning and ventilation system /
- energy saving control model

HTML全文

地铁是城市电力消耗大户，降低运营能耗不仅可以大幅降低运营成本，还能缓解区域电网供电压力。在“碳达峰”与“碳中和”的目标背景下，地铁车站节能改造成为了地铁车站环境控制（简称：环控）系统升级工作的重点^[1-4]。

早期的节能研究主要针对空调水系统（简称：水系统），根据环境反馈误差让变频水泵自动调节频率。通常采用易于实施的基于规则的控制方法，如模糊控制和PID（Proportional Integral Derivative）控制等，相关研究成果已广泛应用^[5-8]。但因未考虑空调通风系统（简称：通风系统）、冷水系统的负荷并非环境实际负荷，该误差最终影响控制系统决策，导致节能效率并非最优。同时，通风系统侧的控制策略也存在类似的问题，即水系统的制冷能力未完全得到应用^[9-10]，仅控制通风系统无法主动降低水系统能耗，为此提出风水联动控制策略^[11-12]，通过从空调系统层面整体考虑，研究通风系统与水系统间的作用关系，实现控制系统对两者得统一控制及负荷匹配。不过，相应的控制方法仅部分优化空调系统内部的控制策略，未考虑车站整体负荷，只能通过规则类控制方法进行调控，其控制效果虽然优于单一变频控制，但仍有很大改进空间^[13]。进一步的研究提出从全局出发应用基于模型的控制方法，通过建立地铁车站系统模型，计算实际需要的冷量，并研究控制系统性能升级^[13-17]，然而，地铁车站建模面临多重挑战，地下复杂结构和运行工况提高了车站负荷模型精度难度^[18]，同时，描述设备的模型同样需要足够精度，此外，还需要考虑诸如客流等大量不确定因素的干扰^[19]，部分研究根据长期采集的数据，结合经验分析，使用理想参数或设计参数预估实际负荷需求，与地铁站实际情况存在偏差。对于空调系统设备的相关研究已很深入，根据已有条件选取经验或半经验模型描述设备特性；对不确定因素的研究多借助预测模型，通过现有系统采集数据构建数据集训练深度神经网络，以预测外部温度和客流量等数据。随着深度神经网络的快速发展，也出现直接通过大量数据集训练得到系统模型的尝试，但该方法受训练集质量影响较大，且训练集构建要求车站已有大量运营采集数据^[20-21]，在更换车站后需要重新微调模型，不具备可移植性。

针对实际负荷需求计算的难点，借助计算流体动力学（CFD，Computational Fluid Dynamics）软件进行计算成为了研究系统瞬态行为的主要方式^[22-26]。此方法将负荷计算精度进一步提高，但计算过程需要消耗巨量资源。此外，CFD类的数值计算对时间步长的设置较为敏感，若划分过细，难以实现较长时间的模拟；反之，则无法保证计算精度。尽管面临诸多挑战，通过建立系统模型并其基础上设计控制系统，仍然是当前主要的设计方法。在环控系统改造中，实现高质量温度控制和降低能耗等多目标，已成为节能控制系统的研究重点^[27-29]。

本文以厦门地铁某车站为研究对象，提出一种基于最优控制的节能控制模型。利用瞬时系统模拟（TRNSYS，Transient System Simulation）程序建立空调通风系统模型，通过与实测数据比对验证模型精度。同时，建立各耗能设备的设备能耗模型，用于分析整体能耗，在该模型基础上验证最优节能控制系统效果。

1 空调通风系统能耗模型

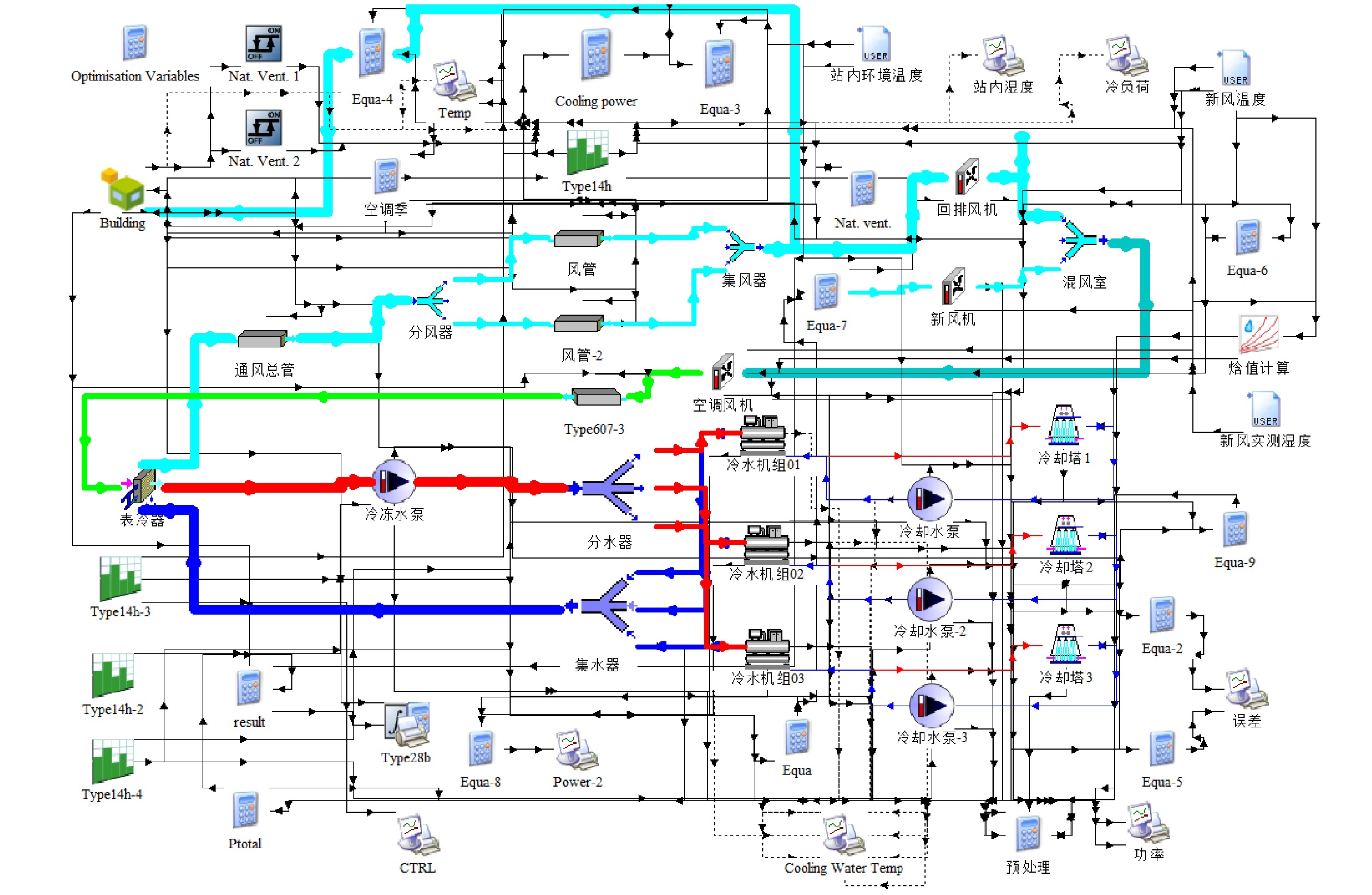
利用厦门某地铁站现场实测设备数据及计算机辅助设计（CAD，Computer Aided Design）图提供的参数，采用TRNSYS 建立地铁车站的空调通风系统能耗模型，其模型如图1所示。该模型包括建筑负荷模型与设备能耗模型，针对同时降低建筑能耗与设备能耗的目标，共同完成参数计算。

图 1 地铁车站的空调通风系统能耗模型

下载: 全尺寸图片幻灯片

1.1 建筑负荷模型

建筑负荷模型采用Building模块，通过传热模型对车站内的温/湿度等环境参数进行计算，提供节能控制方法的效果反馈。

地铁车站内部设备运行环境复杂，负荷计算受诸多不确定因素影响，其中，由人员走动和人员在室内停留产生的热湿负荷，结合实测数据热湿负荷确定为25 kW/h。车站出入口的无规律渗透风受室外环境和站内温度与气压等因素共同影响，根据现场实测数据取车站出入口风量为25 000 m³/h。

1.2 设备能耗模型

设备能耗模型使用了内置单独编写的功率计算模块完成计算并统计，从而得到建筑能耗值。

1.2.1 冷机模型

由于冷机能耗占比远大于其他设备，考虑地铁车站运营状态中各因素对冷水机组产生的影响，使用通用冷水机组模型描述冷机能耗。该模型由Gordon等人于1995年提出，通常称为Gordon-Ng冷水机组模型，即GN模型^[21-32]：

${P_{ch}} = ({Q_{ch}} + A)\frac{{{T_{clwi}}}}{{{T_{chwo}}}} + B{Q_{ch}} + C$

(1)

${Q_{ch}} = \int {c\rho FR\Delta T} {\text{d}}t$

(2)

式（1）中，A、B、C是待定系数； ${P_{ch}}$ 是冷机功率，单位kW； ${T_{clwi}}$ 是冷却水回水温度； ${T_{chwo}}$ 是冷冻水出水温度，单位℃。

式（2）中， ${Q_{ch}}$ 是制冷量； $\rho$ 、 ${\text{c}}$ 分别为水密度和定压比热容； $FR$ 是冷冻水流量，单位m³/h； $\Delta T$ 是冷水机组供回水温度差，单位℃。

根据采集数据使用蒙特卡洛算法（Monte-Carlo）来求解待定参数。

1.2.2 风机模型

空调通风系统中的风机设备能耗使用式（3）模型描述。

$P = {b_0} + {b_1}f + {b_2}{f^2}$

(3)

式（3）中， $b_i$ 是拟合多项式系数； $f$ 是风机频率，取额定功率，单位Hz。空调风机取 ${b_1} = 12$ ， ${b_2} = - 0.89$ ， ${b_3} = 0.025$ ，回排风机取 ${b_1} = 7.5$ ， ${b_2} = - 0.56$ ， ${b_3} = 0.014$ 。

2 基于多目标优化问题的最优控制方法

2.1 问题建立

建立描述控制目标的多目标优化问题模型，并利用权重系数将多目标问题转化成单目标优化问题处理。

$\begin{array}{l}{P}_{0}:\text{ }\underset{f\in X}{\mathrm{min}}\text{ }{\displaystyle \sum _{k=1}^{n}{J}_{k}(t,f)}\\ \quad\quad s.t.\quad{g}_{1}(f)\le 0\text{，}\\ \qquad\qquad{g}_{2}(f)\le 0\text{，}\end{array}$

(4)

式（4）中，t是时间，单位h；g₁( f )是最低频率约束函数，g₂( f )是最高频率约束函数；代价函数 ${J_k}(t,f)$ 由温度误差代价函数J₁(t, f )与设备能耗代价函数J₂(t, f )构成，定义拉格朗日函数为

$\begin{gathered} L(f,\gamma ) = {J_1}(t,f) + {J_2}(t,f) + \sum\limits_{k = 1}^n {{\gamma _k}{g_k}(f)} \\ = \lambda \sum\limits_{i = 1}^n {\left\| {{T_{amb}}(i) - {T_{set}}(i)} \right\|} + \\ {\text{ }}\mu \sum\limits_{j = 1}^n {\int {{P_j}(t,f){\text{d}}t} } + \sum\limits_{k = 1}^n {{\gamma _k}{g_k}(f)} \\ \end{gathered}$

(5)

式（5）中， $\lambda$ ， $\mu$ 是权重系数， $\lambda = 1$ ， $\mu = 0.01$ ； ${T_{amb}}$ 、 ${T_{set}}$ 分别为环境温度与设定温度，单位℃， ${T_{set}} = 28$ ℃； ${P_j}(t,f)$ 是第j个设备当前功率，单位kW； ${\gamma _k}$ 是对应 ${g_k}(f) < 0$ 的拉格朗日乘数，g_k( f )为约束函数。

温度误差和设备功率的累积计算根据实际系统采样频率每3 min进行一次求和。

2.2 不等式约束

空调通风系统风机由空调风机、回排风机和新风机组成，各风机送风量与频率满足连锁关系，设定风机最低频率5 Hz，最高频率45 Hz。

因此频率满足不等式约束。

${g_1}(f) = - \frac{{{Q_2}}}{{{Q_1}}}f + \frac{{50{Q_3}}}{{{Q_1}}} + 5 < 0$

(6)

${g_2}(f) = \frac{{{Q_2}}}{{{Q_1}}}f - \frac{{50{Q_3}}}{{{Q_1}}} - 45 < 0$

(7)

式（6）、式（7）中，50为额定工作频率； ${Q_1}$ 、 ${Q_2}$ 、 ${Q_3}$ 分别是空调风机、回排风机和新风机的额定送风量，单位m³/h； ${f_1}$ 、 ${f_2}$ 分别是空调风机与回排风机频率，单位Hz。

2.3 优化算法求解

2.3.1 优化算法实现

GenOpt是一个基于Java脚本实现的优化算法平台，通过接口实现与TRNSYS之间的变量与参数传递。用户可通过编辑配置文件实现参数设置，以及自定义优化算法。在每次循环开始时，GenOpt会启动TRNSYS 内核开始仿真计算。GenOpt会读取TRNSYS 写入本地文件的仿真数据，包括环境温度、设备能耗等，并调用优化算法对目标函数进行优化。最后，结束本次循环，并将优化结果返回，作为下一次循环中TRNSYS 的初始输入。本文所使用的优化算法均在GenOpt中创建并进行参数配置。

2.3.2 最优化问题求解

使用带Armijo-Goldstein准则的最速下降法求解最优化问题，得到控制量矩阵。

2.3.2.1 Armijo-Goldstein准则

（1）初始化参数 $a > 0,\;\sigma \in (0,1)\;0 < {\gamma _1} < {\gamma _2} < 1\; k = 1$ ；

其中， $\alpha$ 是线搜索初始步长， $\sigma = 0.5$ 是给定的步长调整常数； $\gamma_1=0.2，\; \gamma_2=0.7$ ，是线搜索范围区间的边界。

（2）令 $\alpha = a$ ，若满足：

$\begin{split} f({x_k} + {\alpha _k}{d_k}) - f({x_k}) \leqslant {\gamma _1}{\alpha _k}\nabla f{({x_k})^T}{d_k} , \\ f({x_k} + {\alpha _k}{d_k}) - f({x_k}) \geqslant {\gamma _2}{\alpha _k}\nabla f{({x_k})^T}{d_k} , \end{split}$

则令 ${\alpha _k} = \alpha$ ，停止；否则继续执行（3）。

（3）令 $\alpha = \sigma \alpha$ ， $k = k + 1$ 返回（2）。

2.3.2.2 带Armijo-Goldstein准则的最速下降法

最速下降法通过求解目标函数当前点的梯度确定下降方向，通过Armijo-Goldstein准则确保每次迭代后有足够的前进步长，从而使目标函数值有足够的下降。带Armijo-Goldstein准则的最速下降法实施步骤如下。

（1）设置初始点、迭代次数

$k=1,\ x_k=x_0$

其中， $k$ 是当前循环数； ${x_0}$ 是起始点； ${x_k}$ 是当前循环点。

（2）利用线性逼近方程计算梯度

$\nabla f(x) = \frac{{f(x + \varepsilon ) - f(x)}}{\varepsilon }$

(8)

若 $\nabla f(x) = 0$ ，停止；令 ${d_k} = - \nabla f(x)$ ；

式（8）中， $\nabla f({x_k})$ 是待求解函数在当前循环的点 ${x_k}$ 处的梯度。

（3）调用Armijo-Goldstein线搜索算法计算 ${d_k}$ 方向的步长 ${\alpha _k}$ ，使得满足式（9）

$\left\{ {\begin{array}{*{20}{c}} {f({x_k} + {a_k}{d_k}) \leqslant f({x_k})} \\ {\mathop {\lim }\limits_{k \to \infty } \dfrac{{\nabla f{{(x)}^T}{d_k}}}{{\left\| {{d_k}} \right\|}} = 0} \end{array}} \right.$

(9)

式（9）中， ${\alpha _k}$ 是线搜索算法求解并返回的当前循环的步长， ${d_k}$ 是当前循环的线搜索方向。

（4）令 ${x_{k + 1}} = {x_k} + {\alpha _k}{d_k}$ ，k=k+1，返回（2）

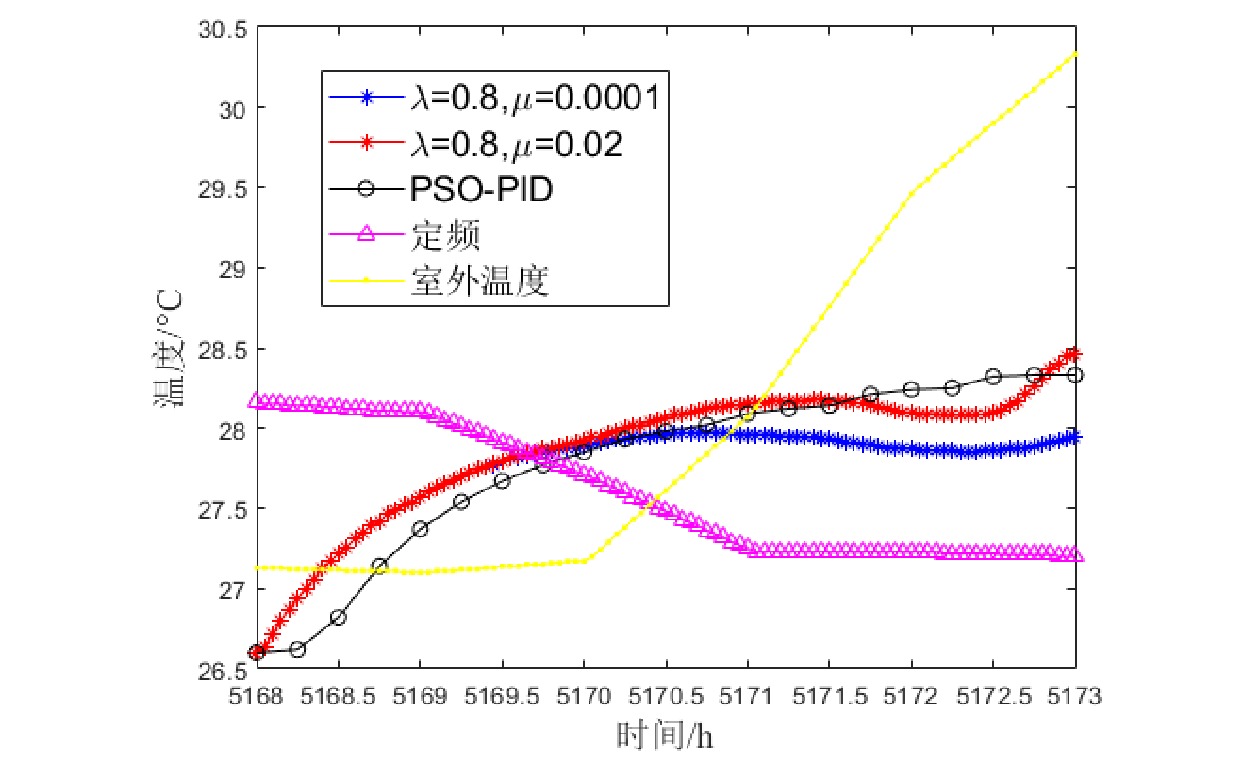
优化求解得到的最优控制方法下的控制量矩阵 ${{{\boldsymbol{C}}}_{opt}} = \left[ {{c_1},{c_2}, \cdots ,{c_n}} \right]$ ，其中， ${c_i}$ 为第i个控制时域内内各个设备的控制量。

3 试验验证

3.1 试验环境

TRNSYS-GenOpt联合仿真试验在Windows11系统环境下进行，仿真计算结果通过Type28模块调用栈保存每一步计算结果并存入本地。

3.2 控制效果

本文选取典型空调季5 h的采集数据，对最优控制方法、基于PSO改进参数的PID控制方法和定频控制方法进行测试，各控制方法下的控制效果如图2所示。

图 2 各控制方法下的室内温度

下载: 全尺寸图片幻灯片

各控制方法的目标均为控制环境温度恒定28℃。基于PSO改进参数的PID控制方法对温度的跟踪效果较好，但相比最优控制方法，其控制动作较慢。最优控制方法经过最少的调整时间达到稳态，且稳态误差小于PSO-PID控制方法。

各控制方法效果及计算耗时如表1所示。在实现温度控制方面，最优控制方法下的2种参数组合效果类似，故表1中给出 $\lambda=0.8，\mu=0.02$ 的情况作为对比，其累积温度误差小于其他模式。在能耗方面相比PSO-PID控制节能8.1%，相比固定频率运行模式节能38.68%。

表 1 计算结果对比

	定频控制	PSO-PID	最优控制 $\lambda = 0.8,\mu = 0.02$
代价函数	0	18.82	19.68
计算时长	0	317 s	824 s
温度误差	31.05	36.55	17.46
能耗函数	261.6	162.698	158.809

下载: 导出CSV

| 显示表格

3.3 权重系数影响效果

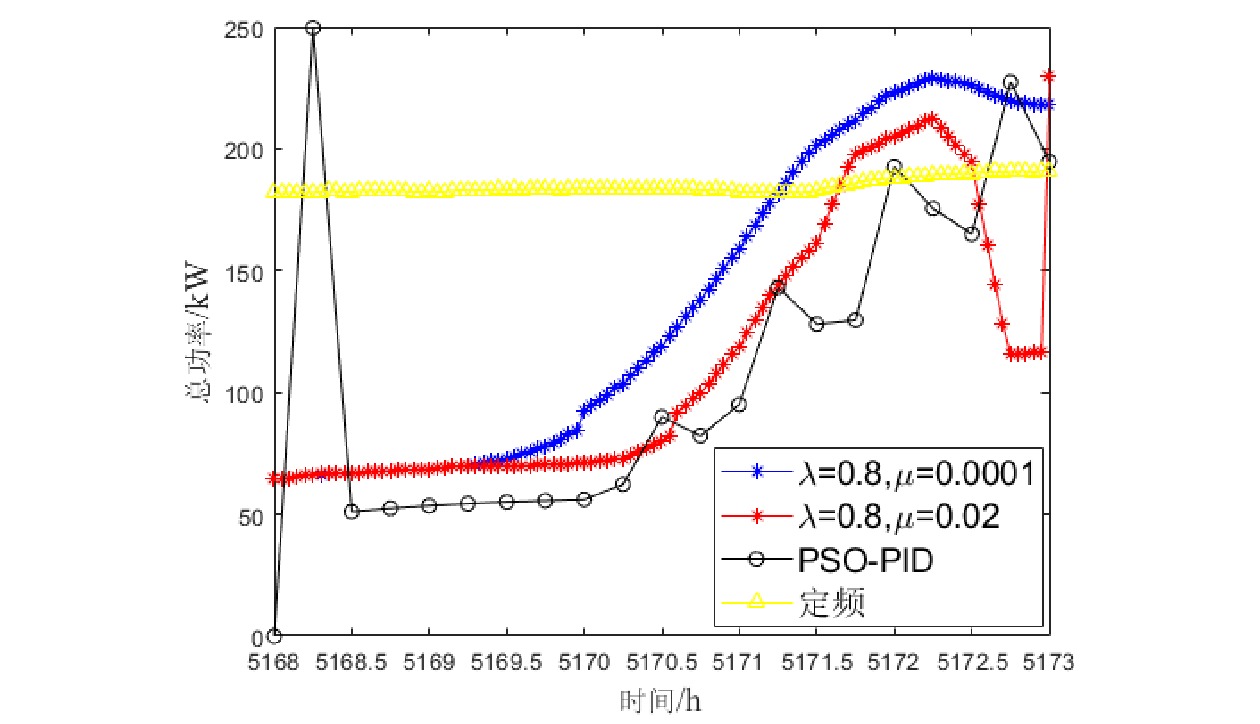
最优控制方法从全局考虑降低能耗代价，以更低的能耗实现了对温度的控制效果，空调通风系统总功率如图3所示。PSO-PID方法尽管能耗最低，但相应的温度误差更大，且出现更多超调。

图 3 空调通风系统总功率

下载: 全尺寸图片幻灯片

如表2所示，取 $\lambda = 0.8$ ，此时 $\mu$ 值的增加将加大对控制器决策的影响，使空调通风系统降低设备功率。

表 2 权重系数影响

	$\mu = 0.001$	$\mu = 0.005$	$\mu = 0.02$
代价函数	14.42	14.96	19.68
温度误差	17.78	17.63	17.46
能耗函数	192.022	172.365	158.809

下载: 导出CSV

| 显示表格

通过分析最优控制方法下的控制矩阵 ${{{\boldsymbol{C}}}_{opt}}$ ，其动作改变速度快于其他方法，在达到稳态后，能够根据模型预测值提前调节，有效降低误差。此外，最优控制方法对温度的稳态误差更加敏感，其通过控制各水泵频率调节水系统的制冷量，实现与建筑冷负荷和风系统冷负荷的实时匹配，防止过量制冷从而降低能耗，达到了降低温度偏差和空调通风系统总能耗的目标，从而提高了节能控制系统的控制性能与经济性。

4 结束语

本文提出一种新的控制方法，通过采用最优控制策略，考虑完整控制周期内的控制效果，对控制量进行预测优化，提高系统稳定性，减少振荡和过度响应。本文负荷模型中，部分影响因素的计算采用理想化假设，并未考虑隧道活塞风等对整体负荷的影响。下一步，将考虑直接处理多目标优化问题，利用多目标粒子群算法等求解帕累托最优解集，得到最优控制矩阵；研究权重系数的取值问题，以平衡舒适度与节能效率的关系；同时，使用进一步改进的优化算法提升优化精度，合理利用硬件计算资源以优化计算负荷，减少计算时长。

图 1 地铁车站的空调通风系统能耗模型

下载: 全尺寸图片幻灯片

图 2 各控制方法下的室内温度

下载: 全尺寸图片幻灯片

图 3 空调通风系统总功率

下载: 全尺寸图片幻灯片

表 1 计算结果对比

	定频控制	PSO-PID	最优控制 $\lambda = 0.8,\mu = 0.02$
代价函数	0	18.82	19.68
计算时长	0	317 s	824 s
温度误差	31.05	36.55	17.46
能耗函数	261.6	162.698	158.809

下载: 导出CSV

表 2 权重系数影响

	$\mu = 0.001$	$\mu = 0.005$	$\mu = 0.02$
代价函数	14.42	14.96	19.68
温度误差	17.78	17.63	17.46
能耗函数	192.022	172.365	158.809

下载: 导出CSV

参考文献(32)

[1]	朱莉莉. 电能质量管理系统及其在城市轨道交通的应用[J]. 铁路计算机应用,2017,26(5):69-72.
[2]	龙广钱,尹逊政. 城市轨道交通列车节能控制策略研究[J]. 铁路计算机应用,2018,27(7):90-94.
[3]	李少波,李严,林菁,等. 基于实测数据的地铁车站公共区空调负荷设计指标优化[J]. 暖通空调,2023,53(3):61-66.
[4]	Simpeh E K, Pillay J P G, Ndihokubwayo R, et al. Improving energy efficiency of HVAC systems in buildings: a review of best practices[J]. International Journal of Building Pathology and Adaptation, 2022, 40(2): 165-182. DOI: 10.1108/IJBPA-02-2021-0019
[5]	姚国梁. 空调变频水泵节能问题探讨[J]. 暖通空调,2004,34(6):32-34.
[6]	杨昭,余龙清,马锋,等. 地铁通风空调系统的逐时优化节能控制策略[J]. 天津大学学报(自然科学与工程技术版),2012,45(7):599-603.
[7]	赵明名,吕子强,沈剑挥. 冷冻水泵节能运行模拟分析[J]. 辽宁科技大学学报,2022,45(1):71-75.
[8]	Homod R Z, Gaeid K S, Dawood S M, et al. Evaluation of energy-saving potential for optimal time response of HVAC control system in smart buildings[J]. Applied Energy, 2020 (271): 115255. DOI: 10.1016/j.apenergy.2020.115255
[9]	闻彪,吴庆,洪学新. 地铁通风空调系统节能研究[J]. 建筑节能,2010,38(4):32-34.
[10]	林晓伟,王侠. 地铁通风空调系统的优化控制[J]. 城市轨道交通研究,2012,15(11):100-104.
[11]	蔡林,李瑞宁,张昆. 地铁车站风水联控节能策略探讨[J]. 机电工程技术,2023,52(8):291-294.
[12]	李元阳,方兴,胡钦,等. 某地铁车站通风空调系统风水联动控制方法及应用[J]. 暖通空调,2023,53(S2):226-231.
[13]	Yildiz O F, Yilmaz M, Celik A. Reduction of energy consumption and CO₂ emissions of HVAC system in airport terminal buildings[J]. Building and Environment, 2022(208): 108632. DOI: 10.1016/j.buildenv.2021.108632
[14]	Trčka M, Hensen J L M. Overview of HVAC system simulation[J]. Automation in Construction, 2010, 19(2): 93-99. DOI: 10.1016/j.autcon.2009.11.019
[15]	Yu Y Z, You S J, Zhang H, et al. A review on available energy saving strategies for heating, ventilation and air conditioning in underground metro stations[J]. Renewable and Sustainable Energy Reviews, 2021(141): 110788. DOI: 10.1016/j.rser.2021.110788
[16]	Yang Y, Hu G Q, Spanos C J. Stochastic optimal control of HVAC system for energy-efficient buildings[J]. IEEE Transactions on Control Systems Technology, 2022, 30(1): 376-383. DOI: 10.1109/TCST.2021.3057630
[17]	陈峥,刘海东,潘雷,等. 基于自适应模型预测控制的地铁车站节能环控系统[J]. 制冷与空调,2023,23(8):60-66,77.
[18]	王丽慧. 地铁活塞风与地铁环控节能[D]. 上海:同济大学,2007.
[19]	Ren Z H, Kim J I, Kim J. Assessment methodology for dynamic occupancy adaptive HVAC control in subway stations integrating passenger flow simulation into building energy modeling[J]. Energy and Buildings, 2023(300): 113667. DOI: 10.1016/j.enbuild.2023.113667
[20]	Xu Y, Gao W J, Qian F Y, et al. Potential analysis of the attention-based LSTM model in ultra-short-term forecasting of building HVAC energy consumption[J]. Frontiers in Energy Research, 2021 (9): 730640. DOI: 10.3389/fenrg.2021.730640
[21]	檀姊静,贺思渝,赵敬源. 地铁车站空调系统瞬态能耗预测模型及应用研究[J]. 西安建筑科技大学学报(自然科学版),2023,55(1):147-153.
[22]	刘巧玲,傅思劼,范波,等. 基于TRNSYS和Fluent相结合的模拟方法[C]//上海市制冷学会2011年学术年会,2011-12-18,上海. 上海:上海市制冷学会,2011.
[23]	葛宣鸣,杜志敏. 建筑空调系统基于TRNSYS-FLUENT的混合仿真研究[C]//上海市制冷学会2015年学术年会,2015-12-18,上海. 上海:上海市制冷学会,2015.
[24]	孟华,孙浩,裴迪,等. 基于聚类及优化集成神经网络的地铁车站空调负荷预测[J]. 同济大学学报(自然科学版),2021,49(11):1582-1589.
[25]	丁瑞华,崔承刚,王逸轩,等. 基于深度强化学习的数据中心空调系统优化控制[J]. 低温与超导,2022,50(9):79-85,100.
[26]	Pandey B, Banerjee R, Sharma A. Coupled EnergyPlus and CFD analysis of PCM for thermal management of buildings[J]. Energy and Buildings, 2021(231): 110598. DOI: 10.1016/j.enbuild.2020.110598
[27]	庄炜茜. 武汉地区地铁车站通风空调系统的节能控制研究[J]. 暖通空调,2010,40(5):39-43.
[28]	张永超,赵录怀,陈永恒. 地铁车站空调水系统自动控制和节能控制系统设计[J]. 工业仪表与自动化装置,2020(2):102-104.
[29]	刘俊,车轮飞,於泽,等. 典型地铁站通风空调控制系统节能改造分析[J]. 暖通空调,2023,53(S2):250-253.
[30]	宋美艳,王亮,朱沁萱. 基于逐时客流量的地铁站空调系统动态负荷研究[J]. 西南科技大学学报,2022,37(2):58-63.
[31]	Gordon J M, Ng K C, Chua H T. Centrifugal chillers: thermodynamic modelling and a diagnostic case study[J]. International Journal of Refrigeration, 1995, 18(4): 253-257. DOI: 10.1016/0140-7007(95)96863-2
[32]	付朋,张吉礼,赵天怡. 中央空调冷水机组性能模型实验研究[J]. 建筑热能通风空调,2016,35(3):1-5.

施引文献(26)

期刊类型引用(23)

1.	韩德志，韩晓艺，华福才，杨良印，邵昕. 数字孪生与多系统融合的城轨综合管控平台研究与实施. 都市快轨交通. 2025(01): 112-119 . 百度学术
2.	钟建峰，韩天，宣秀彬，蔡宇晶，郭顺利. 基于gRPC的城市轨道交通线网运营指挥平台分布式图纸数据同步更新方法. 铁路计算机应用. 2024(07): 74-79 . 本站查看
3.	王贤瑞，光志瑞，陈冉，解柏川，王淞艺. 城市轨道交通智能维修层级及技术研究. 设备管理与维修. 2024(20): 60-64 . 百度学术
4.	刘继平. 轨道交通工务维修管理数字化转型研究. 现代城市轨道交通. 2024(11): 14-20 . 百度学术
5.	钟建峰，孟宇坤，王石生，韩天，蔡宇晶，宣秀彬. 基于gRPC分布式数据通信的地铁线网指挥中心平台设计与实现. 都市快轨交通. 2023(02): 190-197 . 百度学术
6.	杨帆，丁明辉，邓瑾，刘畅，李明. 地铁车辆信息互联共享方案研究. 智慧轨道交通. 2023(02): 26-32 . 百度学术
7.	郭嘉曦. “精益五星”检修现场管理. 中国质量. 2023(03): 113-117 . 百度学术
8.	陶然. 城市轨道交通通信系统智慧运维平台设计. 交通科技与管理. 2023(18): 16-18 . 百度学术
9.	王婷. 城市轨道交通供电智能运维系统研究. 铁道建筑技术. 2023(09): 74-77+188 . 百度学术
10.	孔凡超，吕方林，薛学晓，李华栋. 城市轨道交通车联网综合在途监测系统的研究与应用. 智慧轨道交通. 2023(06): 75-82 . 百度学术
11.	蒋永兵，徐建，王鹏聪. 基于多源数据融合的轨道交通供电智能运维架构研究. 电气化铁道. 2023(S2): 9-12 . 百度学术
12.	党晓勇. 基于云计算的轨道交通机电智能运维平台设计研究. 现代信息科技. 2022(02): 6-8 . 百度学术
13.	李海培. 城市轨道交通云计算技术研究及应用. 自动化与仪表. 2022(05): 99-103 . 百度学术
14.	蔡昌俊，朱小山，邱启盛，王艺达，白丽，张凌云. 广州城际铁路智慧运管系统架构研究与设计. 现代城市轨道交通. 2022(06): 12-16 . 百度学术
15.	鲍飞达，王颖. 浅谈智能化城轨供电运维平台应用层的功能要求. 内蒙古科技与经济. 2022(08): 120+123 . 百度学术
16.	徐余明，黎家靖，张宁，石先明，刘利平，胡祖翰. 基于云-边-端架构的城市轨道交通智能运维系统. 都市快轨交通. 2022(06): 145-150+157 . 百度学术
17.	郑儆醒. 城市轨道交通信号专业智能运维的应用. 电子技术与软件工程. 2021(15): 175-178 . 百度学术
18.	周阳. 城市轨道交通智慧车站设计研究. 江西建材. 2021(09): 150-151 . 百度学术
19.	宣秀彬，高凡，张铭，付思，蔡宇晶. 城市轨道交通智慧出行App的设计与实现. 铁路计算机应用. 2021(10): 69-72 . 本站查看
20.	李璐，王爱丽，王子腾，窦元辰. 基于多源数据融合的城市轨道交通人员综合监测及运营管理系统研究. 铁路计算机应用. 2021(10): 47-53 . 本站查看
21.	张玉福，孔垂云，刘宇，岳阳，王赛. 货运票据电子化部署架构设计与运维保障. 中国铁路. 2021(11): 8-13 . 百度学术
22.	王瑞锋. 基于智能检测监测与大数据技术的城市轨道交通智能运维管理. 现代城市轨道交通. 2021(11): 85-89 . 百度学术
23.	王磊，陆川，蒲丹丹，林意为. 基于改进卷积神经网络的地铁客流量预测算法设计. 现代电子技术. 2021(24): 87-91 . 百度学术

其他类型引用(3)

资源附件(0)

图(3) / 表(2)

计量

文章访问数: 22
HTML全文浏览量: 4
PDF下载量: 5
被引次数: 26

1 空调通风系统能耗模型
1.1 建筑负荷模型
1.2 设备能耗模型
1.2.1 冷机模型
1.2.2 风机模型
2 基于多目标优化问题的最优控制方法
2.1 问题建立
2.2 不等式约束
2.3 优化算法求解
2.3.1 优化算法实现
2.3.2 最优化问题求解
2.3.2.1 Armijo-Goldstein准则
2.3.2.2 带Armijo-Goldstein准则的最速下降法
3 试验验证
3.1 试验环境
3.2 控制效果
3.3 权重系数影响效果
4 结束语

1 空调通风系统能耗模型
1.1 建筑负荷模型
1.2 设备能耗模型
1.2.1 冷机模型
1.2.2 风机模型
2 基于多目标优化问题的最优控制方法
2.1 问题建立
2.2 不等式约束
2.3 优化算法求解
2.3.1 优化算法实现
2.3.2 最优化问题求解
2.3.2.1 Armijo-Goldstein准则
2.3.2.2 带Armijo-Goldstein准则的最速下降法
3 试验验证
3.1 试验环境
3.2 控制效果
3.3 权重系数影响效果
4 结束语

参考文献(32)

施引文献(26)

资源附件(0)

基于最优控制方法的地铁车站节能控制模型

作者简介: 曹扬阳，助理工程师 王晓峻，高级工程师

计量

出版历程