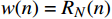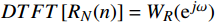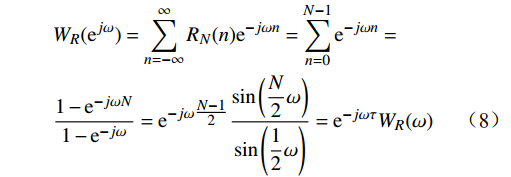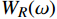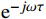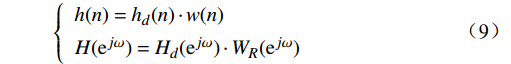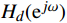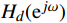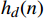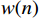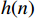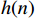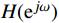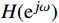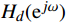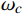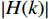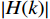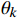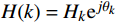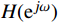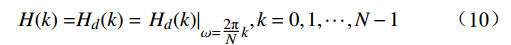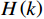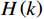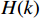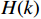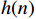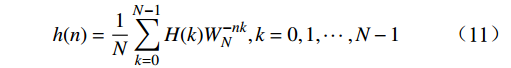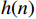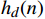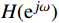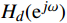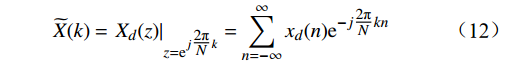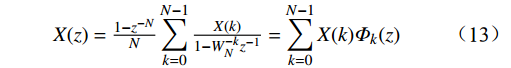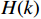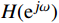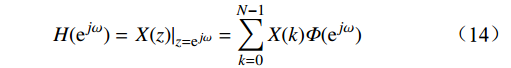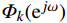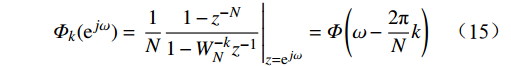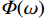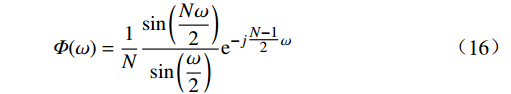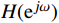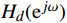Design and analysis of FIR digital filter based on MATLAB
-
摘要:
文章主要研究基于MATLAB实现有限长单位脉冲响应(FIR,Finite Impulse Response)数字滤波器的设计方法,分别从时域和频域两方面对窗函数法和频域采样法进行详细描述,并通过类比两种设计方法的仿真结果,总结其优缺点,可为实际滤波器设计方法的选择提供理论支撑。
-
关键词:
- 有限长单位脉冲响应(FIR) /
- 数字滤波器 /
- MATLAB /
- 窗函数法 /
- 频域采样法
Abstract:This paper mainly studied the design method of Finite Impulse Response (FIR) digital filters based on MATLAB. The paper provided a detailed description of the window function method and frequency domain sampling method from both time and frequency domains, and summarized their advantages and disadvantages by comparing the simulation results of the two design methods. This can provide theoretical support for the selection of practical filter design methods.
-
随着集成电路的飞速发展,对数字信号处理的研究也越来越多。如今,数字信号处理技术已在通信、生物、工业控制、医疗、雷达等领域得到广泛应用[1]。能够对数字信号进行处理的数字滤波器更是数字信号处理中不可或缺的关键器件之一。通过分析数字滤波器结构中是否存在输出到输入的反馈,可将其分为无限长单位脉冲响应(IIR,Infinite Impulse Response)数字滤波器和有限长单位脉冲响应(FIR,Finite Impulse Response)数字滤波器。因FIR数字滤波器具有良好的线性特性,在实际中得到了更为广泛的应用。
数字滤波器的设计可采用软件或硬件实现[2]。本文阐述了从软件角度设计FIR数字滤波器的方法,采用MATLAB软件从基于窗函数法和频域采样法2个途径分别进行了FIR滤波器设计,并分析类比了2种设计方法的特点和优缺点,数据直观,能够更好地分析2种方法的特点,可为实际滤波器设计方法的选择提供理论支撑。
1 FIR数字滤波器设计
1.1 FIR数字滤波器概述
FIR数字滤波器的时域差分方程为[3]
y(n)=N−1∑m=0bmx(n−m) (1) 式(1)中,
bm(m=0,1,⋯,N−1) 是单位脉冲响应序列h(m) ;x(n)为离散信号;n为时域变量;N为序列长度,因此公式(1)也可表示为y(n)=N−1∑m=0h(m)x(n−m) (2) FIR滤波器的单位脉冲响应是有限长的,
h(m) 在0⩽ 范围内有值,其系统函数可表示为H(z) = \sum\limits_{m = 1}^{N - 1} {h(m){z^{ - m}}} (3) 其对应的频率响应为
{H_d}({{\mathrm{e}}^{j\omega }}) = H(z){|_{z = {{\mathrm{e}}^{j\omega }}}} (4) 式(4)中,ω为数字角频率。为直观地分析信号的幅度和相位特性,将其表示为幅度响应和相位响应的形式
{H_d}({{\mathrm{e}}^{j\omega }}) = |{H_d}({{\mathrm{e}}^{j\omega }})|{{\mathrm{e}}^{j{\varphi _d}(\omega )}} = {H_d}(\omega ){{\mathrm{e}}^{j{\varphi _d}(\omega )}} (5) FIR数字滤波器的设计关键即为设计一个实际频率响应函数
H({{\mathrm{e}}^{j\omega }}) ,最大可能地逼近理想的频率响应函数H_d(\mathrm{e}^{j\omega}) 。1.2 窗函数法设计FIR数字滤波器
1.2.1 窗函数法设计原理
窗函数法是从时域角度进行设计[4]。对于给定的理想的FIR数字滤波器参数,以低通滤波器为例,其频率响应函数为
{H_d}({{\mathrm{e}}^{j\omega }}) = \left\{ \begin{array}{l}{{{{\mathrm{e}}^{ - j\omega \tau }},{\text{ }}\left| \omega \right| \leqslant {\omega _c}}} \\{0,{\text{ }}{\omega _c} < \left| \omega \right| \leqslant {{\text{π}}} }\end{array}\right. (6) 式(6)中,τ为中心点。对其作IDTFT(InverseDiscrete-time Fourier Transform),得到理想的单位脉冲响应,公式为
{h_d}(n) = \int_{ - {\omega _c}}^{{\omega _c}} {{H_d}({{\mathrm{e}}^{j\omega }}){{\mathrm{e}}^{j\omega n}}d\omega } = \frac{{\sin \left[ {{\omega _c}(n - \tau )} \right]}}{{\text{π} (n - \tau )}} (7) 由式(7)可看出,理想频域响应得到的单位脉冲响应是一个在时域连续、无限长的信号,且信号以
\tau 为中心偶对称。但从公式(2)可知,FIR数字滤波器的单位脉冲响应是有限长的。因此,如何将无限长的理想单位脉冲响应转变为实际工程应用的有限长单位脉冲响应,并使实际有限长单位脉冲响应对应的频率响应还能够满足设计的指标要求,是窗函数法设计需要解决的关键问题。窗函数法设计思路如图1所示。
本文以矩形窗为例进行窗函数法设计原理分析,假设窗函数表达式为
w(n) = {R_N}(n) ,则通过离散时间傅里叶变换(DTFT,Discrete-time Fourier Transform),DTFT\left[ {{R_N}(n)} \right] = {W_R}({{\mathrm{e}}^{j\omega }}) 得到\begin{split} & {W_R}({{\mathrm{e}}^{j\omega }}) = \sum\limits_{n = - \infty }^\infty {{R_N}(n){{\mathrm{e}}^{ - j\omega n}}} = \sum\limits_{n = 0}^{N - 1} {{{\mathrm{e}}^{ - j\omega n}}} = \\& \frac{{1 - {{\mathrm{e}}^{ - j\omega N}}}}{{1 - {{\mathrm{e}}^{ - j\omega }}}} = {{\mathrm{e}}^{ - j\omega \tfrac{{N - 1}}{2}}}\frac{{\sin \left(\dfrac{N}{2}\omega \right)}}{{\sin \left(\dfrac{1}{2}\omega \right)}} = {{\mathrm{e}}^{ - j\omega \tau }}{W_R}(\omega ) \end{split} (8) 式(8)中,
{W_R}(\omega ) 是幅度谱;{{\mathrm{e}}^{ - j\omega \tau }} 是相位。根据卷积定理时域相乘等于频域卷积,得到\left\{ \begin{array}{l}{{h(n) = {h_d}(n) \cdot w(n)}} \\{H({{\mathrm{e}}^{j\omega }}) = {H_d}({{\mathrm{e}}^{j\omega }}) \cdot {W_R}({{\mathrm{e}}^{j\omega }})}\end{array}\right. (9) 1.2.2 窗函数法设计仿真
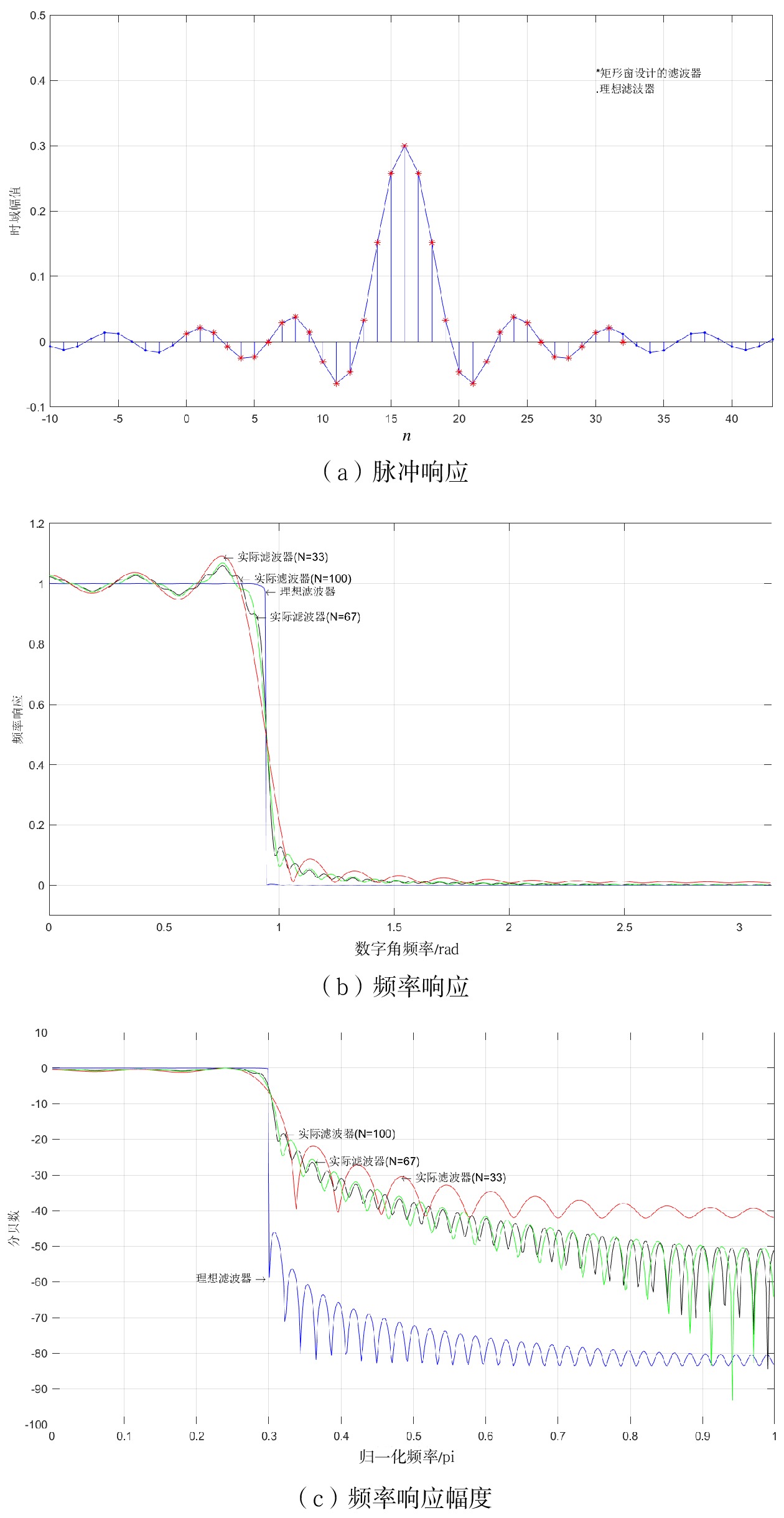
窗函数法设计过程仿真如图2所示。
图2(a)中蓝色圆点为理想低通滤波器对应的无限长单位脉冲响应,红色“*”符号为时域加窗后的实际有限长单位脉冲响应;图2(b)中蓝色线为理想的低通滤波器幅度响应,红、绿、黑这3条线分别为矩形窗的N=33、N=67、N=100对应的频域波形图;图2(c)为窗函数设计法得到的实际滤波器与理想滤波器频率响应的幅度。由图2可知,实际低通滤波器频谱会出现过渡带和震荡起伏的现象。结合公式(8)和公式(9),以及矩形窗函数仿真结果可发现,过渡带带宽与窗函数的形状和N值有关,震荡起伏仅与窗函数的形状有关,常用的窗函数基本参数如表1所示[5]。
表 1 常用窗函数基本参数表窗函数 窗谱性能指标 加窗后滤波器性能指标 旁瓣峰值/dB 主瓣宽度 过渡带宽 \Delta \mathit{\omega } 阻带最小衰减/dB 通带边沿衰减/dB 矩形窗 −13 4{\text{π}} /N 1.8{\text{π}} /N 21 0.815 三角形窗 −25 8{\text{π}} /N 6.1{\text{π}} /N 25 0.503 汉宁窗 −31 8{\text{π}} /N 6.2{\text{π}} /N 44 0.055 海明窗 −41 8{\text{π}} /N 6.6{\text{π}} /N 53 0.021 布莱克曼窗 −57 12{\text{π}} /N 11{\text{π}} /N 74 0.00173 1.2.3 窗函数法设计分析
通过增大N的值可有效改善过渡带带宽问题,但是考虑吉布斯 (Gibbs) 现象的影响,震荡起伏情况无法得到有效改善,因此在实际工程应用中要结合需求选取最合适的窗函数,在满足衰减指标的条件下,考虑计算最优的N值选取。基于窗函数法设计FIR数字滤波器的步骤如下:
(1)根据设计技术指标,写出理想滤波器的频率响应
{H_d}({{\mathrm{e}}^{j\omega }}) ;(2)对
H_d(\mathrm{e}^{j\omega}) 作IDTFT变换,得到理想滤波器的单位脉冲响应{h_d}(n) ;(3)结合给定的技术指标,选取窗函数
w(n) 类型,并通过过渡带带宽计算出N的值;(4)时域加窗,确定实际滤波器的有限长脉冲响应
h(n) ;(5)
h(n) 通过DTFT,计算实际滤波器的频率响应H({{\mathrm{e}}^{j\omega }}) ,并检验H({{\mathrm{e}}^{j\omega }}) 是否满足设计指标要求,若满足则结束,若不满足则修改窗函数或调整N值,直至设计得到的实际滤波器满足设计指标要求。1.3 频域采样法设计FIR数字滤波器
1.3.1 频域采样法设计原理
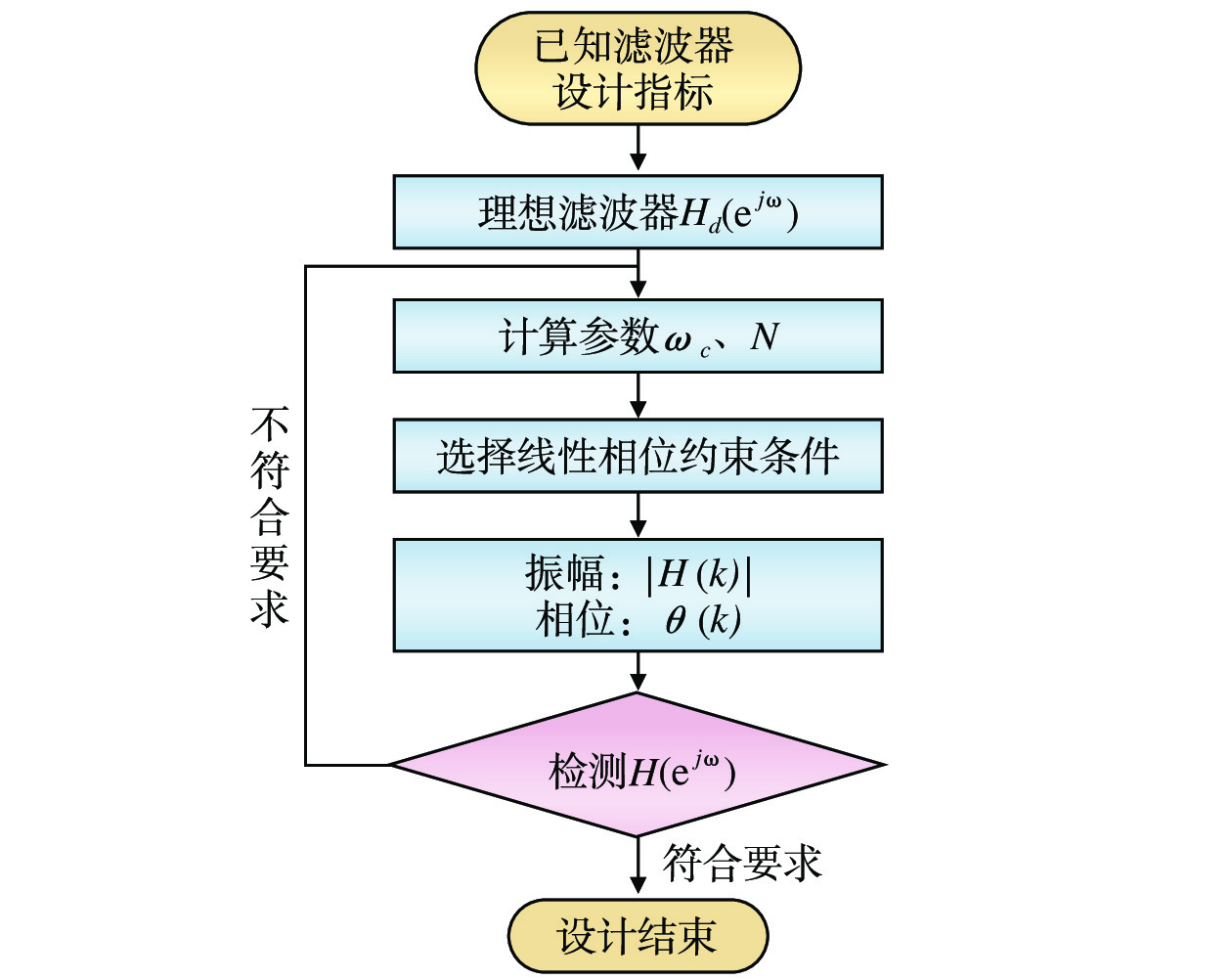
频域采样法是从频域的角度来实现FIR数字滤波器设计的方法。对理想滤波器频率响应等间隔采样,并将其作为实际FIR数字滤波器的频率特性的抽样值。基于频率采样法设计FIR数字滤波器的设计思路如图3所示。
(1)根据给定的滤波器指标,设计理想滤波器频率响应
{H_d}({{\mathrm{e}}^{j\omega }}) ;(2)依据指标暂定
{\omega _c} 和采样点N的取值;(3)选择
\left| {H(k)} \right| 的对称性,写出\left| {H(k)} \right| ,并求出{\theta _k} ;(4)通过将
H(k) = {H_k}{{\mathrm{e}}^{j{\theta _k}}} 带入步骤(3)求得的指标,得到滤波器的频率响应;(5)检验频率响应
H({{\mathrm{e}}^{j\omega }}) 是否满足设计指标要求,若满足则结束,若不满足,则通过过渡带增加采样点和调整N值等方式重修设计滤波器,直至设计所得的滤波器满足设计指标要求。1.3.2 频域采样法设计分析
对本文中公式(4)作频率采样后,得到频率抽样值为
\begin{split} H(k) =& {H_d}(k) = {\left. {{H_d}(k)} \right|_{\omega = \tfrac{{2{\text{π}} }}{N}k}},{{ k = 0,1,}} \cdots {{,N } - 1} \end{split} (10) H\left(k\right) 是由理想滤波器频率响应抽样得到,需要注意的是,不能改变FIR滤波器原始的线性相位特性。因此,H\left(k\right) 的幅度和相位一定要满足线性相位滤波器的约束关系,结合文献[6]分析,具体约束关系如表2所示。表 2 FIR滤波器线性相位约束关系线性相位 采样点N 相频 对称中心 {\mathit{H}}_{\mathit{k}}\mathbf{对}\mathbf{称}\mathbf{性} 特点 一类 奇数 \varphi \left(\omega \right)=-\tau \omega \tau =\dfrac{N-1}{2} {H}_{k}={H}_{N-k} 均可设计 偶数 {H}_{k}=-{H}_{N-k} 不适合高通、带阻 二类 奇数 \varphi \left(\omega \right)=\pm \dfrac{{\text{π}} }{2}-\tau \omega {H}_{k}={-H}_{N-k} 仅可设计带通 偶数 {H}_{k}={H}_{N-k} 不适合低通 得到
H(k) 后,由IDFT定义,通过N个采样值H(k) ,可唯一确定单位脉冲响应h(n) ,即h(n) = \frac{1}{N}\sum\limits_{k = 0}^{N - 1} {H(k)W_N^{ - nk}} ,k = 0,1, \cdots ,N - 1{\text{ }} (11) 频率采样法设计得到的实际单位脉冲响应
h(n) 与理想采样的单位脉冲响应{h_d}(n) 间是不等的关系。找出滤波器实际频率响应H({{\mathrm{e}}^{j\omega }}) 与理想频率响应{H_d}({{\mathrm{e}}^{j\omega }}) 间的联系,是判断频率采样法设计滤波器成功与否的关键。由频域采样定理和频域插值恢复公式\widetilde X(k) = {\left. {{X_d}(z)} \right|_{z = {{\mathrm{e}}^{j\tfrac{{2{\text{π}} }}{N}k}}}} = \sum\limits_{n = - \infty }^\infty {{x_d}(n){{\mathrm{e}}^{ - j\tfrac{{2{\text{π}} }}{N}kn}}} (12) X(z) = \tfrac{{1 - {z^{ - N}}}}{N}\sum\limits_{k = 0}^{N - 1} {\tfrac{{X(k)}}{{1 - W_N^{ - k}{z^{ - 1}}}}} = \sum\limits_{k = 0}^{N - 1} {X(k){\varPhi _k}(z)} (13) 得到频域采样
H(k) 表示H(\mathrm{e}^{j\omega}) 的内插公式H({{\mathrm{e}}^{j\omega }}) = {\left. {X(z)} \right|_{z = {{\mathrm{e}}^{j\omega }}}} = \sum\limits_{k = 0}^{N - 1} {X(k){\varPhi} ({{\mathrm{e}}^{j\omega }})} (14) 公式(14)中,
\mathit{\Phi}_k({\mathrm{e}}^{j\omega}) 通过欧拉公式化简得到{\mathit{\Phi} _k}({{\mathrm{e}}^{j\omega }}) = {\left. {\frac{1}{N}\frac{{1 - {z^{ - N}}}}{{1 - W_N^{ - k}{z^{ - 1}}}}} \right|_{z = {{\mathrm{e}}^{j\omega }}}} = \mathit{\Phi} \left(\omega - \frac{{2{\text{π}} }}{N}k\right) (15) 其中,内插函数
\varPhi (\omega ) 为\mathit{\Phi} (\omega ) = \frac{1}{N}\frac{{\sin \left(\dfrac{{N\omega }}{2}\right)}}{{\sin \left(\dfrac{\omega }{2}\right)}}{{\mathrm{e}}^{ - j\tfrac{{N - 1}}{2}\omega }} (16) 分析公式(14)和公式(15)发现,在采样点上,
H({{\mathrm{e}}^{j\omega }}) 的值与{H_d}({{\mathrm{e}}^{j\omega }}) 一致;但在其他位置,其值是由内插函数的包络叠加而形成,若采样点间的理想频率特性变化越陡,则内插值与理想值的误差越大,因而在理想频率特性的不连续点附近,就会产生肩峰和起伏[7]。在实际工程中,根据设计要求,采用在过渡带增加采样点的方式来减小逼近误差。2 基于MATLAB的FIR数字滤波器设计
设计实现低通滤波器,要求采样频率15 kHz、通带截止频率1.5 kHz、阻带截止频率3 kHz、阻带衰减40 dB,通过MATLAB仿真,得到理想低通滤波器,如图4所示。
2.1 窗函数法设计FIR数字滤波器
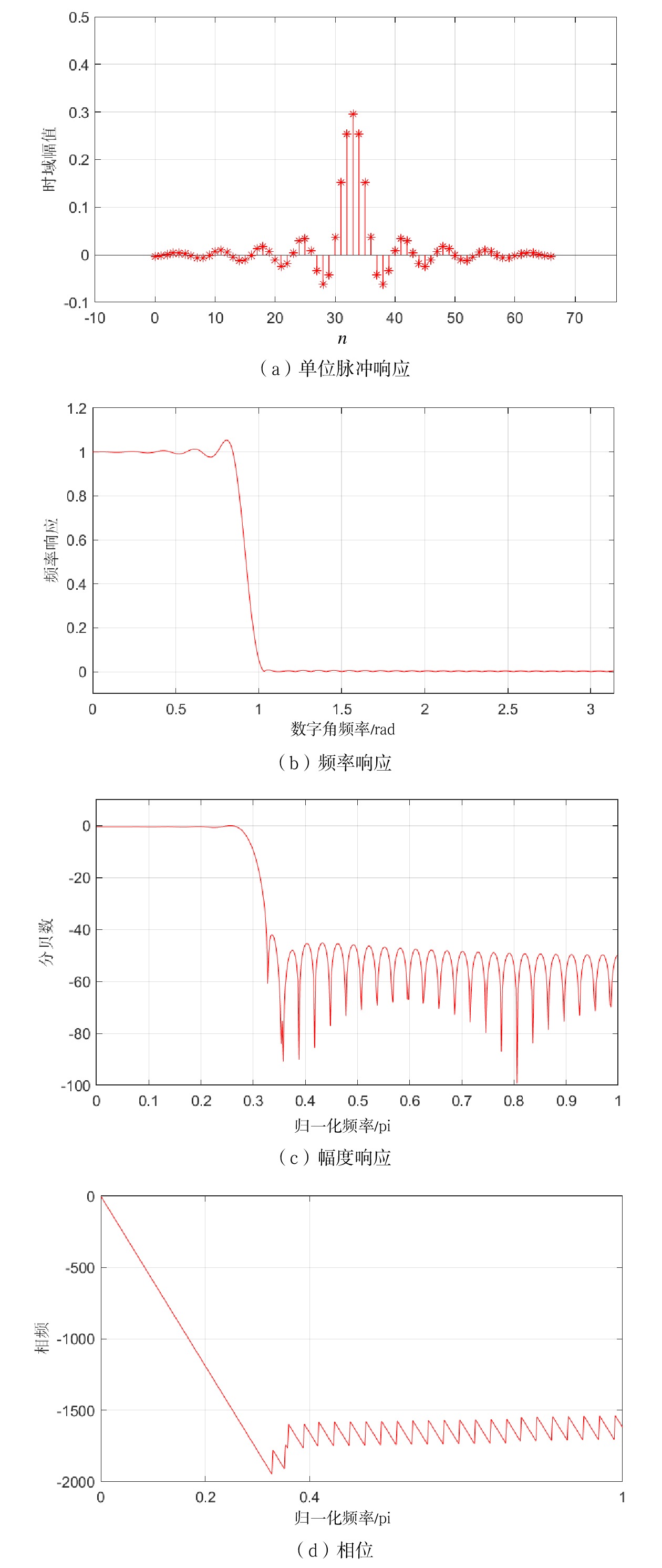
根据表1常见窗函数基本参数表,设计要求达到40 dB衰减,因此选择汉宁窗来实现设计仿真。基于窗函数法设计的FIR数字滤波器如图5所示。
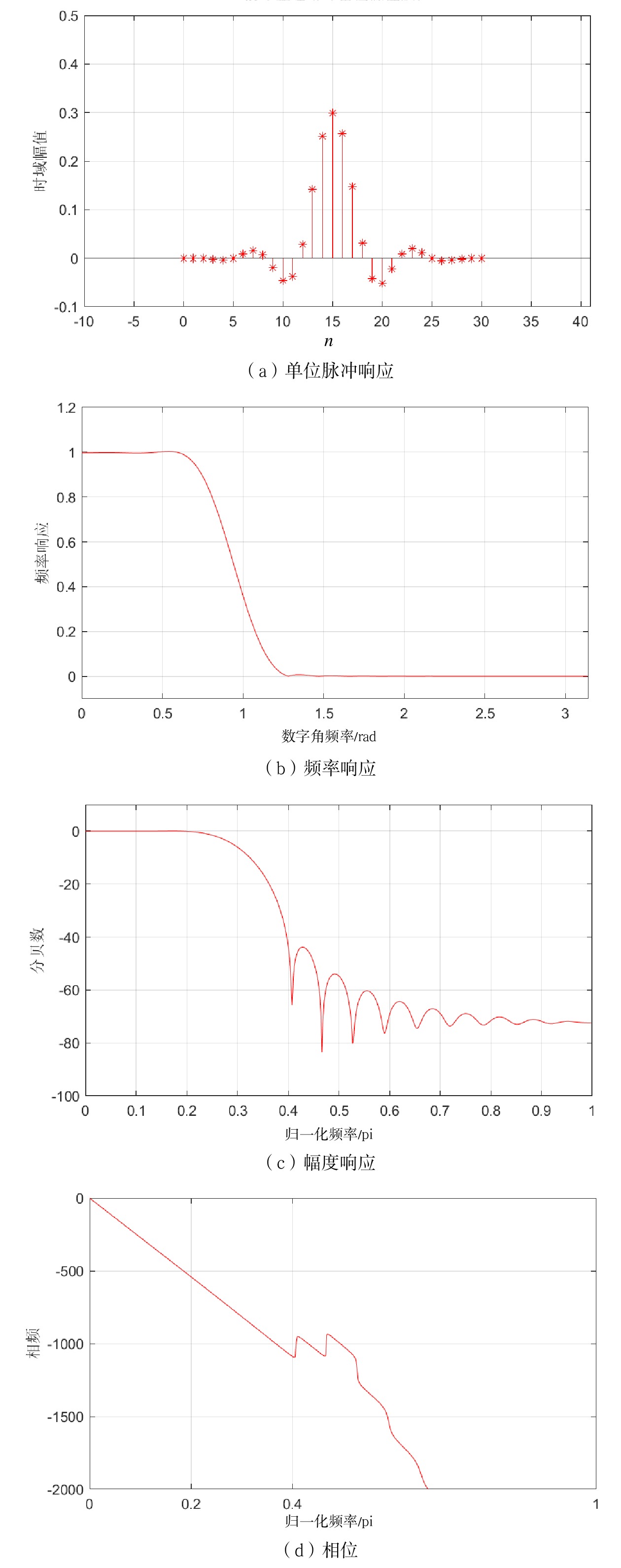
从性能来看,基于窗函数法设计的滤波器已能够满足指标要求,设计得到的滤波器与理想滤波器各项对比分析如图6所示。
由图6(a)可知,时域加窗后得到的实际单位脉冲响应与理想低通的单位脉冲响应相比较,时间变为有限长,窗函数的影响幅度值也有相应的变化。通过图6(b)和图2(b)仿真结果发现,频域上窗函数法设计得到的实际滤波器较理想滤波器相比,存在与窗函数的形状和N值有关的过渡带展宽现象,且受窗函数波形影响频率响应会有震荡起伏。
2.2 频域采样法设计FIR数字滤波器
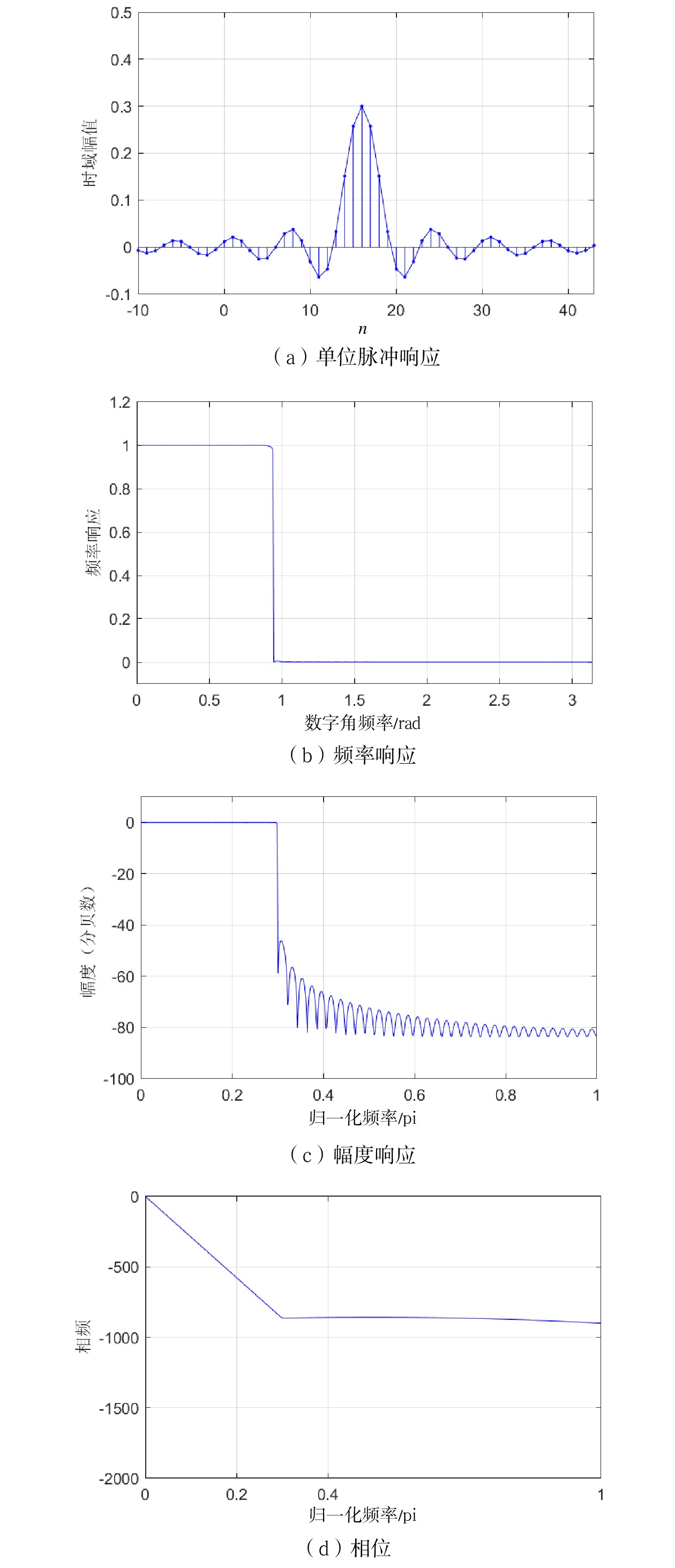
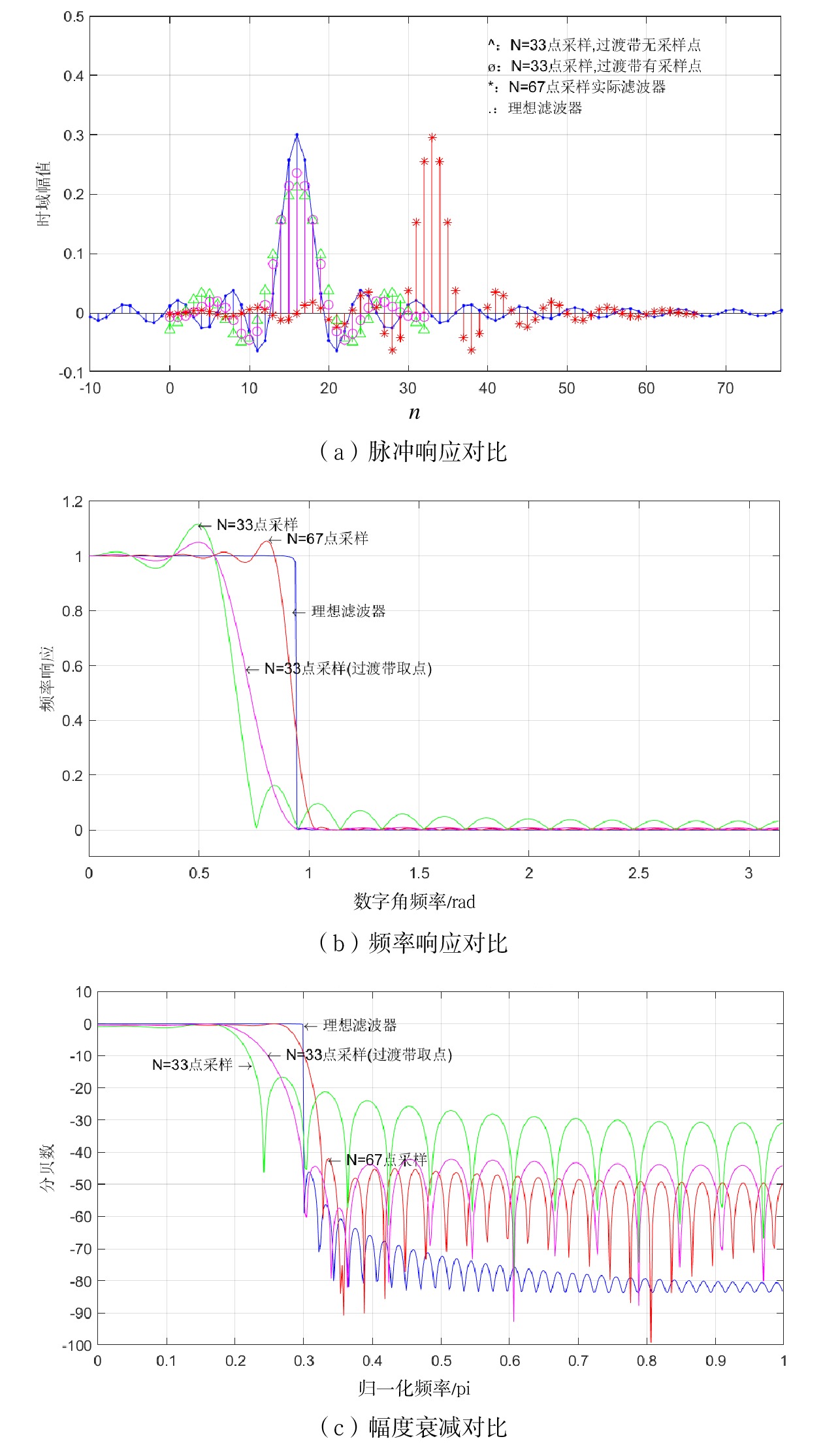
文献[8]中总结了过渡带采样值个数与目标阻带衰减值的关系,根据要求指标,要设计40 dB衰减的FIR数字滤波器,因此,在过渡带放置1个采样点即可满足设计要求。基于频率采样法得到的FIR数字滤波器如图7所示。
基于频率采样法得到的FIR数字滤波器与理想滤波器对比分析如图8所示。由图8(a)可知,频域采样后通过逆傅里叶变换得到的时域信号与理想滤波器脉冲响应信号相比,若采样点数与时域周期匹配,则实际滤波器单位脉冲响应与理想滤波器单位脉冲响应中心点保持一致,但是幅值有差异;当采样点数增加后,中心点发生了移位,但是幅值误差得到了明显的改善。这与频域采样定理的结论吻合,当原始时域序列为无限长,频域采样导致时域周期延拓后,必然会造成时域信号混叠现象[8],因此,实际滤波器的脉冲响应幅度值与理想滤波器存在差异,且若N值越大,即频率采样越密集,则误差越小。由图8(b)和图8(c)可知,当过渡带没有采样点时,由于信号值的突变跳跃,在频率响应上会表现出过渡带边缘出现尖峰和起伏;当在过渡带中增加采样点后,该现象能得到明显改善,且幅度衰减也能得到明显增强。
2.3 方法对比
窗函数法从时域的角度实现FIR滤波器设计,其根本思路为将无限长单位脉冲响应通过加窗截断生成有限长的实际脉冲响应,再通过傅里叶变换得到滤波器实际频率响应,最终通过指标检测判断设计是否成功[9]。频率采样法则是从频域的角度来完成滤波器的设计,通过对理想滤波器的频率响应采样得到,以此将理想滤波器的单位脉冲响应由无限长变为有限长的周期延拓信号,再取主值区间通过傅里叶变换得到实际滤波器的频率响应,最后同样通过指标检测来判断实际滤波器是否满足设计要求。从图6和图8的设计结果对比,基于窗函数法和基于频率采样法设计得到的FIR数字滤波器在选取合适的N点取值、窗函数的前提下都能设计出满足技术指标要求的滤波器。
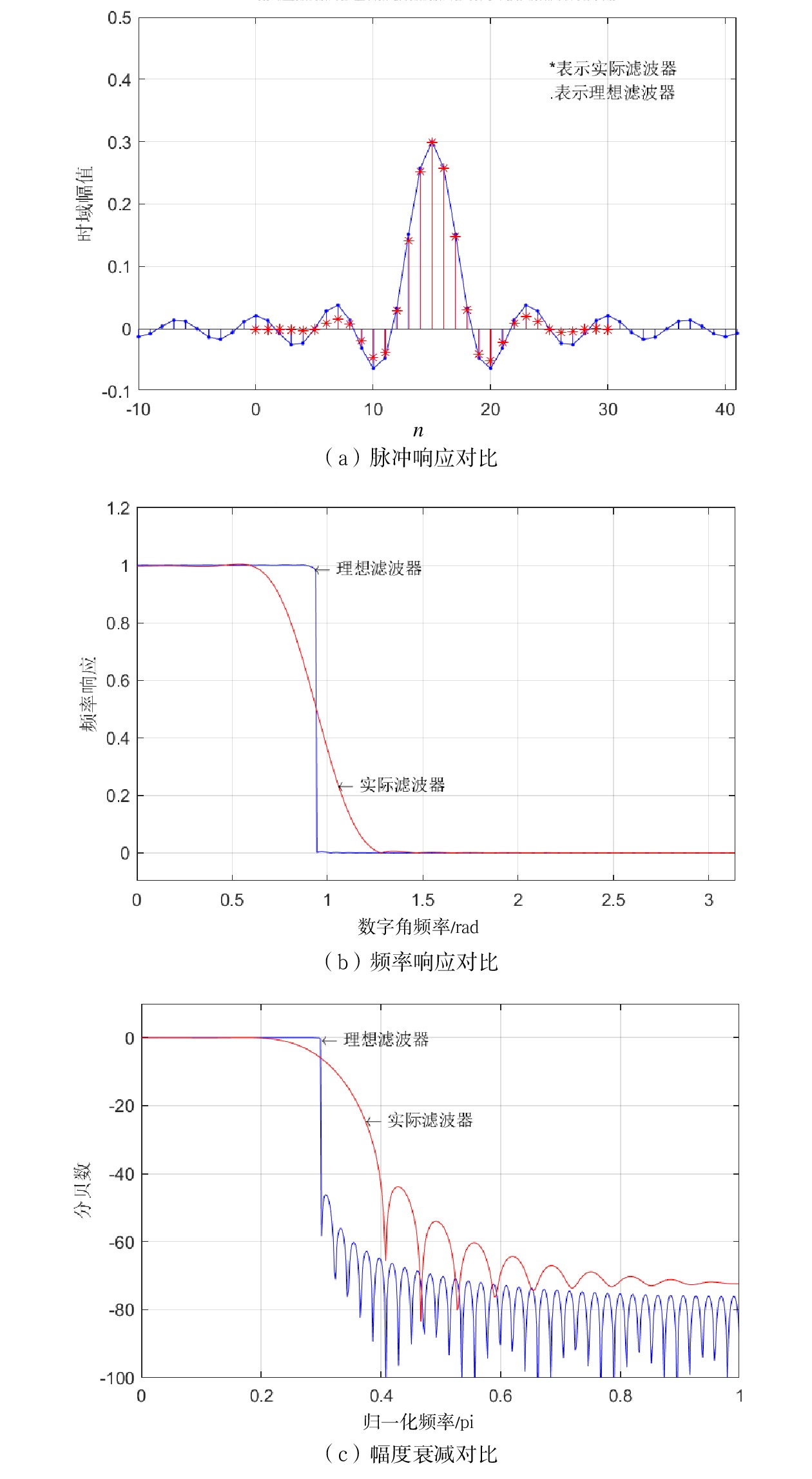
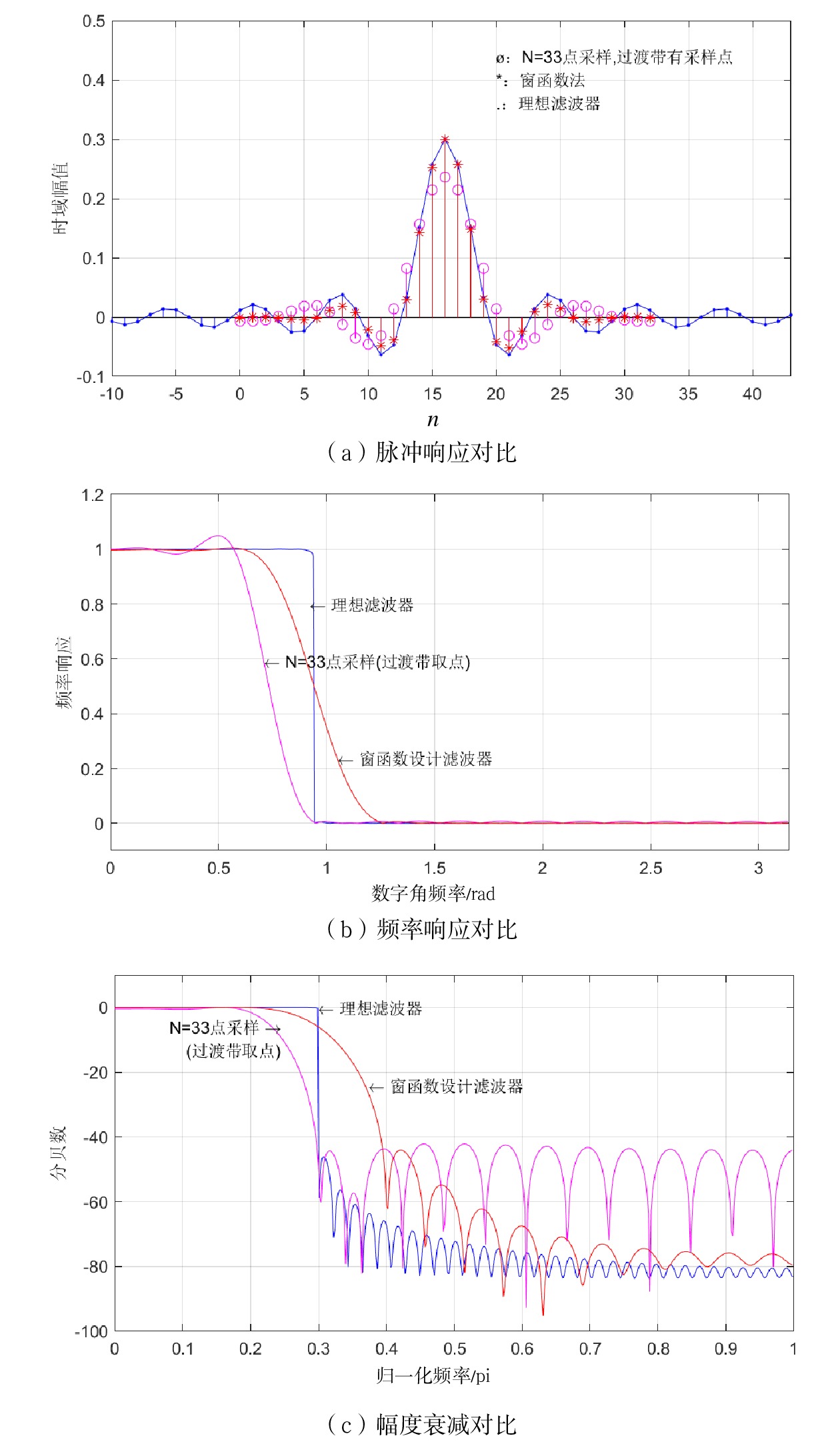
当选取相同的N值时,2种设计法得到的实际滤波器和理想滤波器单位脉冲响应、频率响应、频率响应幅度等指标对比图如图9所示。从中可以看出,当选取相同的N时。窗函数设计法由于在幅值上较好地反映了理想滤波器的单位脉冲响应,因此,其频率响应也更加接近理想滤波器(当频率采样法增加N点采样值后也能得到有效改进),但是其幅度响应较频率采样定理设计得到的实际滤波器衰减更加缓慢。
结合章节2.2、2.3的内容,频率采样法通过过渡带增加采样点及增大采样点N的值能够有效地改善滤波器的性能,可逼近任何给定的频率指标,但同时也会导致计算复杂度增大,该方法适合对滤波器频率要求严格的场景。窗函数法操作简单,通过选择合适的窗函数就能够实现数字滤波器的设计,但由于受窗函数波形影响,存在吉布斯效应,该方法适合在对滤波器性能要求不高时使用。
3 结束语
本文利用MATLAB工具,分别从窗函数法和频率采样法2个途径实现了FIR数字滤波器的设计,并通过与理想滤波器的脉冲响应、频率响应、频率响应幅度等指标进行对比,验证了2种设计方法的可行性,同时给出了不同设计方法的优缺点。本文为后续的数字信号处理研究提供了理论基础。
-
表 1 常用窗函数基本参数表
窗函数 窗谱性能指标 加窗后滤波器性能指标 旁瓣峰值/dB 主瓣宽度 过渡带宽 \Delta \mathit{\omega } 阻带最小衰减/dB 通带边沿衰减/dB 矩形窗 −13 4{\text{π}} /N 1.8{\text{π}} /N 21 0.815 三角形窗 −25 8{\text{π}} /N 6.1{\text{π}} /N 25 0.503 汉宁窗 −31 8{\text{π}} /N 6.2{\text{π}} /N 44 0.055 海明窗 −41 8{\text{π}} /N 6.6{\text{π}} /N 53 0.021 布莱克曼窗 −57 12{\text{π}} /N 11{\text{π}} /N 74 0.00173 表 2 FIR滤波器线性相位约束关系
线性相位 采样点N 相频 对称中心 {\mathit{H}}_{\mathit{k}}\mathbf{对}\mathbf{称}\mathbf{性} 特点 一类 奇数 \varphi \left(\omega \right)=-\tau \omega \tau =\dfrac{N-1}{2} {H}_{k}={H}_{N-k} 均可设计 偶数 {H}_{k}=-{H}_{N-k} 不适合高通、带阻 二类 奇数 \varphi \left(\omega \right)=\pm \dfrac{{\text{π}} }{2}-\tau \omega {H}_{k}={-H}_{N-k} 仅可设计带通 偶数 {H}_{k}={H}_{N-k} 不适合低通 -
[1] 屈召贵. 基于窗函数法的FIR数字滤波器设计[J]. 信息技术与网络安全,2019,38(9):85-89, DOI: 10.19358/j.issn.2096-5133.2019.09.017. [2] 李红科,王庆春. 基于MATLAB的FIR数字滤波器设计[J]. 微型电脑应用,2024,40(5):85-87,103. DOI: 10.3969/j.issn.1007-757X.2024.05.022 [3] 贾君霞. 基于MATLAB的FIR滤波器设计的探讨[J]. 自动化与仪器仪表,2014(12):110,112. [4] 蒋梦影,陶敬荣. 基于MATLAB的FIR滤波器的三种设计方法的比较[J]. 数字通信世界,2019(11):243. DOI: 10.3969/J.ISSN.1672-7274.2019.11.205 [5] 徐 晗. 基于窗函数与频率采样法的FIR滤波器仿真与实现[J]. 电子测试,2022,36(20):39-41, DOI: 10.16520/j.cnki.1000-8519.2022.20.045. [6] 黄 波. 基于频率采样法的FIR数字滤波器仿真与实现[J]. 科学技术创新,2020(33):122-123. [7] 程佩青. 数字信号处理教程[M]. 5版. 北京:清华大学出版社,2017. [8] 龙 安,陈 华. 基于MATLAB的频率采样法设计FIR滤波器[J]. 广西科学院学报,2011,27(1):68-70, DOI: 10.13657/j.cnki.gxkxyxb.2011.01.012. [9] 陈纯楷. 数字信号处理基础教程[M]. 北京:清华大学出版社,2018.




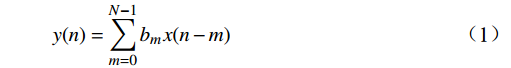
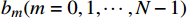
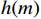
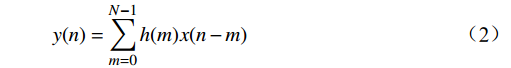
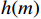
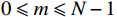


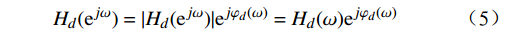
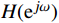
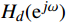
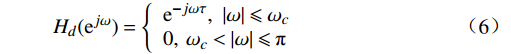
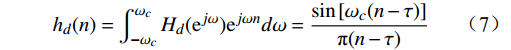
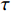

 下载:
下载: