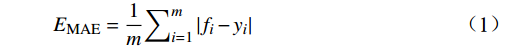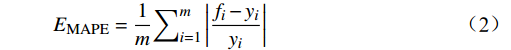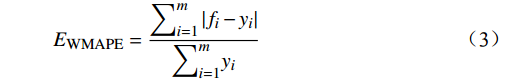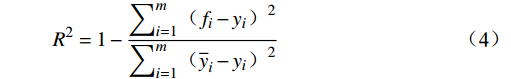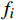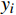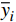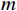Prediction model for daily surplus of freight transportation based on machine learning regression algorithm
-
摘要:
针对承运制清算对铁路局集团公司货物运输（简称：货运）收入及营业收入的影响，为贯彻落实 “以承运盈余目标为导向”的货运经营理念，实现货运经营效益最大化，文章运用多种机器学习回归算法，针对每项货运承运费用分别构建预测模型，并根据不同算法模型在测试集上的多项评估指标的表现，选定一种最佳模型，进行货运承运运费和承运对外付费每日按票预测，从而提前掌握每日承运盈余结果。研究表明，极端森林回归（ETR ，Extra Trees Regressor）算法多项评估指标均表现最好，运用其构建的模型可更为精准地实现货运承运日盈余预测。截至2024年4月，该预测模型共完成约
1033 万张货票相关承运费用的预测，整体预测误差率在1.7%以下，充分发挥了数据要素价值，为货运效益分析及经营决策等提供数据支撑。Abstract:In order to implement the freight management concept of "surplus oriented transportation" and maximize the efficiency of freight management, this paper used multiple machine learning regression algorithms to construct prediction models for each freight transportation cost, and selected the best model based on the performance of different algorithm models on multiple evaluation indicators on the test set, predicted freight charges and external payments by ticket on a daily basis, in order to gain an early understanding of the daily shipping surplus results. The research results indicate that the Extra Trees Regression (ETR) algorithm performs the best in multiple evaluation indicators, and the model constructed using it can implement more accurate prediction of daily freight earnings. As of April 2024, the prediction model has completed predictions for approximately 10.33 million freight bills related to transportation costs, with an overall prediction error rate of less than 1.7%. It fully utilizes the value of data elements and provides data support for freight benefit analysis and business decision-making.
-
自2018年中国国家铁路集团有限公司（简称：国铁集团）推行以承运制清算为主的运输进款办法以来，铁路货物运输（简称：货运）业务改为以货物发送企业为承运企业，并按承运货票为基础单元逐票清算的模式[1]。随着铁路货运承运制清算的深入推进，建立了公开、公平、公正的铁路货运清算秩序，提高了铁路运输企业拓展市场的积极性和主动性。然而，随着新质生产力赋能铁路高质量发展要求的日益紧迫，铁路货运承运工作的数字化、智能化已成为有效途径和必然趋势。目前，铁路运输企业在运输进款与承运效益分析中存在对市场变化不敏感、业财融合不深入、数字化水平滞后等问题，制约了货运清算预测分析的科学性和时效性，影响了货运经营效益预判及经营决策。承运制清算中每张货票只有在完成全程运输并产生完整工作量数据后才能清算（至少1个月），其滞后性使得相关部门不能及时精确掌握当日货运承运收入数据，无法满足收入分析快速反应市场的管理要求，不能适应效益优先的经营理念。
在该领域的研究中，赵晨等人[2]总结了现行货运承运制清算办法研究和提出的过程，包括其总体框架、清算项目设计及清算单价测算，并提出基于总线原理的货运承运制清算模型构建方法；马长青[3]利用运输生产源数据和国铁集团资金中心清算数据进行串联的信息，将运输生产源点信息和清算数据进行分析对比，构建清算收入与运输组织过程联动的铁路局集团公司（简称：局）清算收入测算模型。上述方法多从清算收入构成等角度构建测算分析模型，缺少人工智能、大数据等新技术手段的应用。谢大锋等人[4]基于k近邻算法进行货运承运制清算未到达货票清算预测，该方案仅选择一种机器学习模型进行清算数据的预测，缺乏完整性。
基于上述现状，本文运用机器学习回归算法和大数据技术，通过货票基础数据和清算历史数据的清洗汇聚、特征工程、模型训练及选择等，构建基于机器学习回归算法的货运承运日盈余预测模型（简称：本文模型），最终实现对当日货运承运货票将要产生的承运（对外）付费和承运运费的提前预测，得出承运日盈余预测结果，提前掌握货运承运效益，为铁路企业货运经营决策提供了数据支撑，促进货运经营业务数字化水平的提高。
1 业务数据准备
1.1 相关费用介绍
本文研究的货运承运日盈余是指局承运运费扣除承运付费中付外局部分（简称：承运对外付费）后的剩余费用。承运运费包括基准运费和运价高出部分[5]，其中，运价高出部分包含“高出归局”和“高出归己”。承运付费包含线路使用费、车辆服务费、机车牵引费、到达服务费、综合服务费，其中，前4项为全付费（付本局和付外局）。承运对外付费包括线路使用费付外局、车辆服务费付外局、机车牵引费付外局、到达服务费付外局和综合服务费。其中，综合服务费全部支付给国铁集团清算平台[5]，没有付本局部分，因此综合服务费全付费即为综合服务费对外付费。
1.2 原始数据收集
本文运用大数据分析技术整合来自各系统、各业务部门的数据资源以实现数据的贯通和共享[6-7]。结合PDI（Pentaho Data Integration）构建了ETL（Extract-Transform-Load）数据汇聚与调度监控平台，完成对铁路货运承运清算数据的整合入库及过程监控，形成清算历史库，并于每日定时读取货票信息管理系统、现车系统、集装箱运输信息系统等的相关原始数据，通过清洗、转换和入库程序，完成基础数据整合，形成货票基础数据库。清算历史库和货票基础数据库共同提供本文模型构建所需要的原始已清算货票数据。
2 特征工程
2.1 数据项分析
在原始已清算货票数据中，数据项有近百项，在评估了货运承运日盈余预测任务后，初步剔除了与任务不相关和含义重复的数据项，如车号、品名汉字等，初筛后剩余32个数据项。这些数据项可分为数值型、时间型和类别型。
（1）对于数值型数据项，需要评估其分布趋势，了解数据的分布特征。通过平均数和中位数，可掌握数据的集中趋势；通过最大/小值，可初步判断是否有异常值；通过标准差、偏态系数和峰态系数可判断是否符合正态分布。部分数值型数据项的分布特征基本指标如表1所示，由表1可看出，大部分数据项均不符合正态分布，因此，在后续的数据处理中需要进行标准化、归一化操作。
表 1 部分数值型数据项的分布特征基本指标平均数 中位数 最小值 最大值 标准差 偏态系数 峰态系数 总里程 1516.50/km 711/km 4.00/km 5739.00/km 1445.49/km 0.79 −0.86 计费重量 60.60/t 64/t 0.00 3780.00/t 84.20/t 37.69 1482.58 计费重量合计 358.46/t 64/t 0.00 68200.00/t 3542.40/t 12.46 164.53 总重量 83.55/t 86.2/t 10.89/t 5105.50/t 111.59/t 38.58 1530.24 货物总重量 60355.94/kg 64000/kg 0.00 3780000.00/kg 84251.92/kg 37.63 1479.70 国铁运费 7475.50/元 4556.1/元 0.00 538075.96/元 8720.41/元 10.05 406.90 地铁运费 2437.35/元 1860.46/元 0.00 131927.34/元 3028.91/元 6.34 165.98 运费合计 9915.32/元 5583.58/元 11.30/元 670003.30/元 10589.48/元 10.54 433.33 （2）时间型数据项包括制票日期、统计日期、清算年月等，根据业务专家经验，其对于承运费用预测没有直接关系，因此剔除。
（3）类别型数据项包括部企标志、货票票种、货票类型、货运中心等，这些数据项之间不存在大小关系，后续需要对其进行特征编码操作。
2.2 数据处理
本文通过特征构造的方式构造了管内直通（管内指局管辖范围内，直通指局管辖范围外）、运费合计、管内内燃里程、管内电力里程等特征；采用标签编码的方式对类别型特征进行处理；以货票为单位剔除存在缺失值的数据；使用StandardScaler方法对所有数值型特征进行了标准化处理，使每个特征的数据都尽可能满足均值为0、标准差为1的正态分布，防止过拟合现象。
2.3 相关性分析
机器学习中，相关性分析有助于理解特征与目标变量间的关系，从而对特征选择给予一定的参考依据。如图1所示，本文选择皮尔逊热力图表达部分数值型货票特征和目标费用（以车辆服务费为例）之间的线性关系，图1中，数据是皮尔逊相关系数，其数值越接近1，表示两个变量之间的正相关性越强。由图1可以看出，车辆服务费与管内电力里程、本局里程合计、外局里程合计、总里程、国家铁路运输企业收取的费用（简称：国铁运费）、运费合计等有较强的线性相关性。但有些特征和目标之间可能存在非线性关系，因此在特征选择时，还需要综合考虑业务背景、数据特点、模型性能等多个因素，并需要多次迭代和调整。
2.4 特征选择
特征选择是指从原始数据中选择与目标变量间最相关或最具预测能力的特征子集，以提高模型的性能和泛化能力。特征选择有助于减少特征空间的维度，去除冗余和噪声特征，提高模型的解释性和效率。本文广泛收集了承运清算业务相关专家意见，结合货运承运相关业务知识和数据相关性分析，选择12种不同的费用，构造不同的特征，最终从近百项特征中为每项费用筛选出了十几个特征作为后续模型训练的输入，常见的特征有货票票种、货票类型、发站、到站、管内直通、本局里程合计、外局里程合计、总里程、国铁运费、运费合计等。
3 预测模型搭建
本文运用scikit-learn机器学习库，通过数值计算扩展包numpy、pandas等实现数据计算和分析，以货运承运货票为基础单元，分别构建前述12种费用的机器学习预测模型。
3.1 模型构建
将经过特征筛选后获得的相对规范的历史数据分为3个部分：采用某局2021年7月—2022年8月的货票及清算数据作为训练集；采用2022年9月—2022年12月的货票及清算数据作为验证集；采用2023年1月—2023年4月的货票及清算数据作为测试集。
回归算法的选择通常取决于业务的需要，不同的回归算法具有不同的特点和适用范围，因此，在选择时需要考虑业务场景、数据特点、任务目标等因素。本文选择了随机森林回归（RFR，Random Forest Regression）[8]、梯度提升回归（GBR，Gradient Boosting Regressor）[9]、极端森林回归（ETR，Extra Trees Regressor）[10]、XGBRegressor（Extreme Gradient Boosting Regressor）[11]及stack融合模型等5种算法分别对12项费用进行建模。
3.2 模型评估
3.2.1 性能评价指标
采用MAE（Mean Absolute Error）、MAPE（ Mean Absolute Percentage Error）、WMAPE（Weighted Mean Absolute Percentage Error）和R2等评价指标对已训练好的上述5种模型在测试集上的效果进行综合评估和筛选，其公式为
$$ E_{{\mathrm{MAE}}}=\frac{1}{m}{\sum }_{i=1}^{m}\left|{f}_{i}-{y}_{i}\right| $$ (1) $$ E_{{\mathrm{MAPE}}}=\frac{1}{m}{\sum }_{i=1}^{m}\left|\frac{{f}_{i}-{y}_{i}}{{y}_{i}}\right| $$ (2) $$ E_{{\mathrm{WMAPE}}}=\frac{{\displaystyle\sum }_{i=1}^{m}\left|{f}_{i}-{y}_{i}\right|}{{\displaystyle\sum }_{i=1}^{m}{y}_{i}} $$ (3) $$ {R}^{2}=1-\frac{{\displaystyle\sum }_{i=1}^{m}{（{f}_{i}-{y}_{i}）}^{2}}{{\displaystyle\sum }_{i=1}^{m}{（{\overline{y}}_{i}-{y}_{i}）}^{2}} $$ (4) 式（1）～式（4）中，
$ {f}_{i} $ 为预测值；$ {y}_{i} $ 为真实值；$ {\overline{y}}_{i} $ 为真实值均值，$ m $ 为样本个数。MAE能更好地反映预测值误差的实际情况；MAPE指标可了解预测结果与真实值之间的相对误差程度；WMAPE可用来评估承运盈余预测的整体误差；R2的取值范围为[0,1]，越接近1，表明模型数据拟合的越好。3.2.2 模型评估与分析
部分费用在5类算法模型上MAE的表现如图2所示、 WMAPE的表现如表2所示、R2的表现如表3所示。
表 2 部分费用在5类模型上的WMAPE费用类型 RFR GBR ETR XGBR stack 线路使用费 17.311‰ 22.950‰ 16.694‰ 17.949‰ 16.577‰ 线路使用费_对外 17.366‰ 20.322‰ 16.679‰ 17.650‰ 16.749‰ 车辆服务费 0.047‰ 0.319‰ 0.021‰ 0.251‰ 0.045‰ 车辆服务费_对外 3.282‰ 6.405‰ 1.861‰ 2.153‰ 1.911‰ 基准运费 0.040‰ 0.033‰ 0.012‰ 1.569‰ 0.077‰ 平均数 7.609‰ 10.006‰ 7.053‰ 7.914‰ 7.072‰ 表 3 部分费用在5类模型上的R2费用类型 RFR GBR ETR XGBR stack 线路使用费 0.9807 0.9730 0.9810 0.9814 0.9810 线路使用费_对外 0.9856 0.9791 0.9864 0.9863 0.9864 车辆服务费 0.9915 0.9913 0.9915 0.9911 0.9913 车辆服务费_对外 0.9910 0.9900 0.9914 0.9912 0.9912 基准运费 0.9879 0.9864 0.9881 0.9879 0.9881 平均数 0.9873 0.9840 0.9877 0.9876 0.9876 由图2、表2和表3可看出，采用ETR算法的预测模型的MAE值和WMAPE最小，且R2值更接近1，说明其具有较好的拟合效果。因此，本文最终选择基于ETR算法的模型进行货运承运日盈余各项相关费用的预测。
4 应用情况
本文基于ETR算法的预测模型，结合可视化和大数据分析技术，搭建货运承运日盈余大数据预测分析平台，实现对承运日盈余预测结果的存储、展示和综合分析。货运承运日盈余分析页面展示效果如图3所示。该平台已在中国铁路乌鲁木齐局集团有限公司（简称：乌局）投入实际应用，主要应用于货运承运日盈余测算分析、盈余目标劈分与进度超欠及兑现分析、固定流向各品类不同运输方式承运效益测算分析、辅助货运营销决策及预决算指标劈分等。
2021年8月至2024年4月，该平台共完成超过
1033 万张货票的货运承运日盈余预测，整体预测的WMAPE在17‰以下，取得了较好的应用效果。本文预测模型在实际应用中的预测结果如表4所示。表 4 本文预测模型在实际应用中的预测结果费用项目 实际值/万元 预测值/万元 WMAPE 承运盈余 163392.36 163154.04 1.459‰ 承运运费 330079.23 330038.87 0.122‰ 基准运费 321777.96 321788.11 0.032‰ 高出归己 4876.72 4890.57 2.84‰ 高出归局 3424.55 3360.18 18.794‰ 承运付费（全付费） 260678.86 262755.55 7.966‰ 车辆服务费 48930.37 48945.97 0.319‰ 到达服务费 10316.04 10313.10 0.285‰ 机车牵引费 106734.26 107672.30 8.789‰ 线路使用费 72356.24 73564.10 16.694‰ 综合服务费 22341.95 22260.09 3.664‰ 承运付费（对外付费） 166686.87 166884.83 1.188‰ 车辆服务费 29177.35 29246.11 2.357‰ 到达服务费 5694.49 5628.75 11.545‰ 机车牵引费 66192.92 65747.93 6.723‰ 线路使用费 43280.16 44001.94 16.677‰ 综合服务费 22341.95 22260.09 3.664‰ 5 结束语
本文研究构建的基于机器学习回归算法的货运承运日盈余预测模型，实现了对货运承运日盈余的及时精准预测。基于此预测构建的货运承运日盈余大数据预测分析平台，经过在乌局的应用验证，效果良好，打通了货运、财务多系统间的数据壁垒，为货运经营决策提供了科学的数据支撑，提升了货运经营业务数字化水平。
由于货运业务复杂多变，政策调控无法实时掌握，后续需要建立较为健全的模型监督机制，及时更新预测模型；深入分析不同费用分项，并根据各项费用特点，优化特征筛选方法和模型训练参数，进一步提高模型预测的准确率。
-
表 1 部分数值型数据项的分布特征基本指标
平均数 中位数 最小值 最大值 标准差 偏态系数 峰态系数 总里程 1516.50/km 711/km 4.00/km 5739.00/km 1445.49/km 0.79 −0.86 计费重量 60.60/t 64/t 0.00 3780.00/t 84.20/t 37.69 1482.58 计费重量合计 358.46/t 64/t 0.00 68200.00/t 3542.40/t 12.46 164.53 总重量 83.55/t 86.2/t 10.89/t 5105.50/t 111.59/t 38.58 1530.24 货物总重量 60355.94/kg 64000/kg 0.00 3780000.00/kg 84251.92/kg 37.63 1479.70 国铁运费 7475.50/元 4556.1/元 0.00 538075.96/元 8720.41/元 10.05 406.90 地铁运费 2437.35/元 1860.46/元 0.00 131927.34/元 3028.91/元 6.34 165.98 运费合计 9915.32/元 5583.58/元 11.30/元 670003.30/元 10589.48/元 10.54 433.33 
下载: 导出CSV
表 2 部分费用在5类模型上的WMAPE
费用类型 RFR GBR ETR XGBR stack 线路使用费 17.311‰ 22.950‰ 16.694‰ 17.949‰ 16.577‰ 线路使用费_对外 17.366‰ 20.322‰ 16.679‰ 17.650‰ 16.749‰ 车辆服务费 0.047‰ 0.319‰ 0.021‰ 0.251‰ 0.045‰ 车辆服务费_对外 3.282‰ 6.405‰ 1.861‰ 2.153‰ 1.911‰ 基准运费 0.040‰ 0.033‰ 0.012‰ 1.569‰ 0.077‰ 平均数 7.609‰ 10.006‰ 7.053‰ 7.914‰ 7.072‰
下载: 导出CSV
表 3 部分费用在5类模型上的R2
费用类型 RFR GBR ETR XGBR stack 线路使用费 0.9807 0.9730 0.9810 0.9814 0.9810 线路使用费_对外 0.9856 0.9791 0.9864 0.9863 0.9864 车辆服务费 0.9915 0.9913 0.9915 0.9911 0.9913 车辆服务费_对外 0.9910 0.9900 0.9914 0.9912 0.9912 基准运费 0.9879 0.9864 0.9881 0.9879 0.9881 平均数 0.9873 0.9840 0.9877 0.9876 0.9876
下载: 导出CSV
表 4 本文预测模型在实际应用中的预测结果
费用项目 实际值/万元 预测值/万元 WMAPE 承运盈余 163392.36 163154.04 1.459‰ 承运运费 330079.23 330038.87 0.122‰ 基准运费 321777.96 321788.11 0.032‰ 高出归己 4876.72 4890.57 2.84‰ 高出归局 3424.55 3360.18 18.794‰ 承运付费（全付费） 260678.86 262755.55 7.966‰ 车辆服务费 48930.37 48945.97 0.319‰ 到达服务费 10316.04 10313.10 0.285‰ 机车牵引费 106734.26 107672.30 8.789‰ 线路使用费 72356.24 73564.10 16.694‰ 综合服务费 22341.95 22260.09 3.664‰ 承运付费（对外付费） 166686.87 166884.83 1.188‰ 车辆服务费 29177.35 29246.11 2.357‰ 到达服务费 5694.49 5628.75 11.545‰ 机车牵引费 66192.92 65747.93 6.723‰ 线路使用费 43280.16 44001.94 16.677‰ 综合服务费 22341.95 22260.09 3.664‰
下载: 导出CSV
-
[1] 中国铁路总公司. 铁路货物运输进款清算办法(试行):铁总财[2017]333号[R]. 北京:中国铁路总公司,2017. [2] 赵 晨,吕成文,唐恩斌. 基于总线原理的铁路货运承运清算模型构建与应用[J]. 铁道经济研究,2023(2):12-16. [3] 马长青. 铁路局集团公司级货运清算收入测算分析模型的构建与应用[J]. 铁道运输与经济,2023,45(10):148-155. [4] 谢大锋,安 腾,霍鹏敏. 基于大数据的未到达货票清算预测平台研究[J]. 铁路计算机应用,2019,28(10):35-38. [5] 中国铁路总公司. 中国铁路总公司关于修订《铁路货物运输进款清算办法(试行)》部分内容的通知:铁总财[2019]19号[Z]. 北京:中国铁路总公司,2019. [6] 中国国家铁路集团有限公司. “十四五”铁路网络安全和信息化规划:铁科信[2022]16号[Z]. 北京:中国国家铁路集团有限公司,2022. [7] 中国国家铁路集团有限公司. 数字铁路规划:铁科信[2023]105号[Z]. 北京:中国国家铁路集团有限公司,2023. [8] Breiman L. Random forests[J]. Machine Learning, 2001, 45(1): 5-32. DOI: 10.1023/A:1010933404324
[9] Friedman J H. Greedy function approximation: a gradient boosting machine[J]. The Annals of Statistics, 2001, 29(5): 1189-1232. DOI: 10.1214/aos/1013203450
[10] Geurts P, Ernst D, Wehenkel L. Extreme gradient boosting for regression and time series forecasting[J]. Machine Learning, 2006, 64(1): 41-64.
[11] Chen TQ, Guestrin C. XGBoost: a scalable tree boosting system[C]//Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 13-17 August, 2016, San Francisco, USA. New York, USA: ACM, 2016. 785-794.
-
期刊类型引用(0)
其他类型引用(1)
计量
- 文章访问数: 56
- HTML全文浏览量: 10
- PDF下载量: 21
- 被引次数: 1
