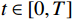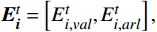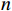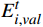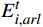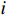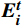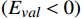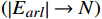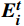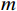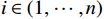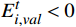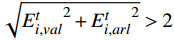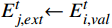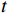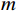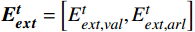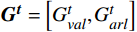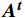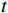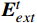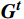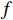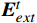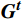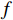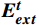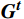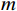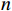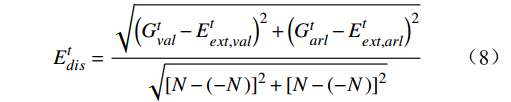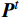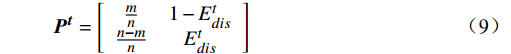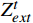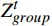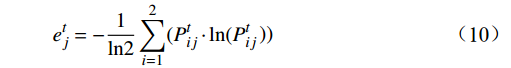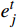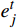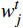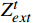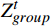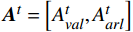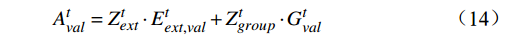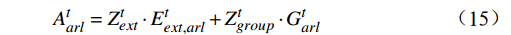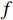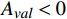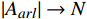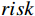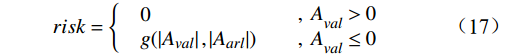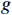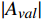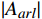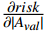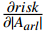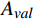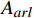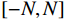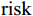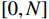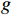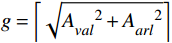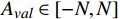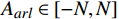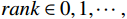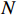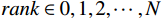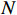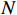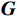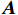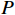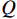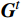Intelligent computing and emergency decision-making analysis of group emotional atmosphere in passenger transport place
-
摘要:
为实现对铁路客运场所安全监控中潜在风险的识别,针对群体情感分析展开研究,提出了一种基于客运场所群体情感氛围智能计算的应急决策分析方法。构建了客运场所旅客群体情感氛围的计算与分析模型,该模型由群体情感氛围量化模型和群体情感氛围分析模型两部分组成;基于上述模型,实现了对突发事件的风险等级估计,以及相应的应急预案响应。通过在IEMOCAP数据集和自制数据集上的实验验证,结果表明,所提出的方法能够有效识别多人场景中的群体情感变化,可为铁路客运场所的安全管理与应急响应提供技术支持。
Abstract:To identify potential risks in the safety monitoring of railway passenger transport place and conduct research on group emotion analysis, this paper proposed an emergency decision-making analysis method based on intelligent computing of group emotional atmosphere in passenger transport place. The paper constructed a computing and analysis model for the emotional atmosphere of passenger groups in passenger transportation place. The model consisted of two parts: a quantitative model for the emotional atmosphere of the group and an analysis model for the emotional atmosphere of the group. Based on the above model, it was implemented risk level estimation of emergencies and corresponding emergency response plans. Through experiment verification on the IEMOCAP dataset and self-made dataset, the results show that this method can effectively identify group emotional changes in multi person scenarios, provide technical support for safety management and emergency response in railway passenger transport place.
-
随着我国铁路的快速发展, 2023年,全国铁路旅客发送量创历史新高[1]。为保障中国铁路的高质量发展,大力推进现代化产业体系建设,加快发展新质生产力势在必行[2]。智能运营场景中,通过自动化、智能化技术,保障铁路客运场所的旅客安全,构建能够快速检测安全隐患的智能监控系统,是铁路管理部门的重要需求,也是技术赋能生产的重要实践。传统室内公共场所的安全监测方法,依靠大量安保人员全天候观察监控录像,十分依赖人工,易发生漏报、误报等问题。且传统监测系统在突发事件的应急决策上缺乏智能自动预警功能,其预警和应急决策依然依赖于人工,容易造成险情延误。
智能监控系统的研发,可解放安保人员生产力,提高智能运营效率,保障旅客出行安全。Narayanan等人[3]提出了一种使用深度学习和人体行为检测方法用来检测公共场所中的异常事件,该系统在触发了预设条件时会自动向上级部门发出警报,初步实现了监控系统的自动预警功能;Rhalem等人[4]针对音频中的暴力事件进行检测,在视频数据中提取暴力状态下人体不稳定运动模式,以检测其是否有攻击性运动。当前,基于视频、音频的异常状况预警研究仍存在以下局限:(1)异常检测仅专注于个体行为,无法应对室内公共场所环境的复杂性;(2)异常识别仅能针对已发生的异常事件,应急预案存在滞后性,无法识别潜在风险。
针对上述局限,本文尝试从两方面进行探索:(1)建立适合客运场所的群体情感感知模型,尽早识别群体中的异常行为;(2)探索基于群体情感氛围分析的应急决策方法,尽早触发应急预案处置。
基于文本、音频、视频监测数据的群体情感感知与识别是近年来新兴的研究领域,在公共安全[5]、突发事件安全监控等领域具有巨大的经济价值[6]。Dai等人[7]提出一种基于全局场景特征和局部人脸特征的群体情感识别算法,该算法考虑了情感在群体间的传播和局部面部特征,提高了群体情感识别的准确性;Hou等人[8]提出一种多模态公共场所异常识别算法,该算法将群体行为识别和语音情感识别相结合,并通过最大权重多模态信息融合算法进行情感氛围估计,从而预警和报警可能的危险行为。上述方法考虑了多模态下群体情感的重要性,但没有对群体情感给出具体量化规则。同时,以上均为离散情感模型,无法满足复杂群体情感氛围监测的实际需求。本文在上述研究基础上,进一步给出多人场景下群体情感氛围模型的数学表达,提高方法的可解释性。
向良云[9]指出,聚集人群的群体心理,对群体性事件演化升级具有直接推动作用。铁路旅客人群密度高,安全管控难度大,若能在客运场所的预警管控应急预案体系中,配合群体情感氛围感知与智能决策技术,构建一套快速有效的突发事件应急响应模式,尽早发现潜在的危险突发事件、尽快智能唤醒应急预案,对于促进与完善铁路交通突发事件的预警管控应急预案体系,实现客运场所智能运营,具有重要的社会意义和安全经济价值。
综上,本文构建客运场所群体情感氛围计算与分析模型,基于群体情感氛围分析的应急决策算法,建立更加具有实时性的应急预案与动态响应机制,从而提升对突发事件的应急响应速度。
1 客运场所群体情感氛围计算与分析模型
本章节的主要工作是构建群体情感氛围计算与分析模型,用于触发应急预案。针对客运场所人流密集、旅客情感波动大等特点,提出一个能够反映个体情感与群体平均情感之间相互关系的数学模型。该数学模型通过考虑个体与群体的极端情感的互相影响,计算出群体情感氛围,目的是为了后续在达到设定的风险阈值时触发相应的应急预案,通过对个体情感与群体情感的量化,提高对突发事件的预警能力。
1.1 群体情感氛围分析基础
在进行群体情感识别时,应注意到以火车站为例的客运场所具有的特点:客运场所往往人流密集,且旅客呈现疲劳紧张、易兴奋、易受环境影响、情感波动性大等多种不稳定状态。
设
\boldsymbol{E}\boldsymbol{_i} 为个体i 的情感向量;\boldsymbol{G} 为群体平均情感向量;定义传染效应为{{\boldsymbol{E}}}_{{\boldsymbol{i}}}\to {{\boldsymbol{E}}}_{{\boldsymbol{ext}}}\Rightarrow {\boldsymbol{G}}={f}_{1}\left({\boldsymbol{G}},{{\boldsymbol{E}}}_{{\boldsymbol{ext}}}\right)\to {{\boldsymbol{E}}}_{{\boldsymbol{ext}}} (1) 定义极化效应为
{\boldsymbol{G}}\to {{\boldsymbol{G}}}_{{\boldsymbol{ext}}}\Rightarrow{{\boldsymbol{E}}}_{{\boldsymbol{i}}}={f}_{2}({\boldsymbol{G}},{{\boldsymbol{E}}}_{{\boldsymbol{i}}})\to {{\boldsymbol{G}}}_{{\boldsymbol{ext}}} (2) 公式(1)和(2)中,
\boldsymbol{E}_{{\boldsymbol{ext}}} 为个体极端情感向量;{f}_{1} 为情感传染函数;\boldsymbol{G}_{{\boldsymbol{ext}}} 为群体极端情感向量;{f}_{2} 为群体极化函数;\boldsymbol{G}\to\boldsymbol{E}_{{\boldsymbol{ext}}} 为情感的传染效应向量;\boldsymbol{E}_{\boldsymbol{i}}\to\boldsymbol{{\boldsymbol{G}}}_{{\boldsymbol{ext}}} 为情感的群体极化效应向量。1.2 群体情感氛围量化模型
使用Russell的效价−唤醒模型(Valence-Arousal Model)[10]构建本文模型。效价−唤醒模型中,情感状态可通过效价
{E}_{val} 和唤醒{E}_{arl} 来描述。{E}_{val} 表示情感的积极性,定义域为E_{val}\in[-\mathrm{\mathit{N}},\mathrm{\mathit{N}}] ,{E}_{val} < 0 表示消极情感,{E}_{val} > 0 表示积极情感,\mathrm{\mathit{N}} 为应急决策模型中的风险等级层级;{E}_{arl} 表示情感的强度,定义域为E_{arl}\in[-\mathrm{\mathit{N}},\mathrm{\mathit{N}}] ,其中,{E}_{arl} < 0 表示沉郁,{E}_{arl} > 0 表示激动,{E}_{arl}=0 表示平静。一名旅客的情感\boldsymbol{E_i} 可视为一个二维向量\boldsymbol{E}_{\boldsymbol{i}}=[E_{i,val},E_{i,arl}] ,{E}_{i,val} 与{E}_{i,arl} 是相互独立的,模型示意如图1所示,任意{{\boldsymbol{E}}}_{{\boldsymbol{i}}} 均可对应到图1中的一个点。对于
t\in [0,T] 时刻单人情感\boldsymbol{E}_{\boldsymbol{i}}^t=\left[E_{i,val}^t,E_{i,arl}^t\right], i\in(1,\cdots,n) ,其中,n 为公共场所环境下视频采集到的人数;{E}_{i,val}^{t} 和{E}_{i,arl}^{t} 分别为个体i 在效价和唤醒维度上的情感量化。参考文献[11]基于音视频双模态的多级LSTM的多模态情感融合方法,得到个体的单人情感
{{\boldsymbol{E}}}_{{\boldsymbol{i}}}^{{\boldsymbol{t}}} 。在此基础上,关注个别旅客是否存在极端情感,即关注是否存在个体的效价状态为消极({E}_{val} < 0) 且唤醒状态较极端(\left|{E}_{arl}\right|\to N) 。本文提出的个体极端情感识别算法的伪代码如下。输入:单人情感
{{\boldsymbol{E}}}_{{\boldsymbol{i}}}^{{\boldsymbol{t}}} 输出:具有极端情感倾向的人数
m ,及他们各自的情感值1:初始化环境
2:for all
i\in (1,\mathrm{ }\cdots ,n) 3: if
{E}_{i,val}^{t} < 0 &\sqrt{{{E}_{i,val}^{t}}^{2}+{{E}_{i,arl}^{t}}^{2}} > 2 :4:
{E}_{j,ext}^{t}{\leftarrow E}_{i,val}^{t} 5: j=j+1
6: end if
7: end for
计算
t 时刻具有极端情感倾向的人数m 及群体极端情感倾向向量\boldsymbol{E}_{{\boldsymbol{ext}}}^{\boldsymbol{t}}=\left[E_{ext,val}^t,E_{ext,arl}^t\right] ,即具有极端情感倾向的人群的平均情感值,公式为{E}_{ext,val}^{t}=\frac{\displaystyle\sum _{j=1}^{m}{E}_{j,val}^{t}}{m} (3) {E}_{ext,arl}^{t}=\frac{\displaystyle\sum _{j=1}^{m}{E}_{j,arl}^{t}}{m} (4) 通过对所有个体情感求平均,得出群体平均情感向量
\boldsymbol{G}^{\boldsymbol{t}}=\left[G_{val}^t,G_{arl}^t\right] ,公式为{G}_{val}^{t}={\bar{E}}_{i,val}^{t} (5) {G}_{arl}^{t}={\bar{E}}_{i,arl}^{t} (6) 1.3 群体情感氛围分析模型
如1.1所述,在客运场所群体情感氛围分析问题中,应同时考虑到情感传染效应与极化效应对旅客群体情感的影响。因此,本文提出客运场所的群体情感氛围分析模型的数字表达式为
{{\boldsymbol{A}}}^{{{t}}}=f({{\boldsymbol{E}}}_{{{ext}}}^{{{t}}},{{\boldsymbol{G}}}^{{{t}}}) (7) 式(7)中,
\boldsymbol{A}^{\boldsymbol{t}} 为时刻t 客运场所的群体情感氛围向量;{{\boldsymbol{E}}}_{{{ext}}}^{{{t}}} 为识别到的个体极端情感向量;\boldsymbol{G}^{\boldsymbol{t}} 为群体平均情感向量,即群体情感氛围受到个体极端情感与群体平均情感的双重影响;f 为个体极端情感\boldsymbol{E}_{{{ext}}}^{{t}} 和群体平均情感\boldsymbol{G}^{\boldsymbol{t}} 的加权融合函数。本节将对客运场所环境的函数f 进行推导。本文参考文献[12]的熵值法,提出了一种客运场所群体情感融合算法,该方法使用熵值法的计算结果作为加权依据,对多模态信息进行加权融合。熵值法考虑两个指标间的相互关系,满足公式(1)和(2)中对
\boldsymbol{E}_{{\boldsymbol{ext}}}^{\boldsymbol{t}} 和\boldsymbol{G}^{\boldsymbol{t}} 互相影响的分析。同时,熵值法可避免人为因素对指标权重的干扰,从而增强综合评价结果的客观性。将极端情感人数
m 在总人数n 中的占比和极端情感与群体情感倾向间的距离作为估计指标,分别在效价和唤醒维度上计算极端情感与群体情感在两类指标上的权重。将极端情感与群体情感倾向间的距离进行归一化,公式为{{{E}}}_{{{dis}}}^{{{t}}}=\frac{\sqrt{{\left({{G}_{val}^{t}-E}_{ext,val}^{t}\right)}^{2}+{\left({{G}_{arl}^{t}-E}_{ext,arl}^{t}\right)}^{2}}}{\sqrt{{[N-(-N\left)\right]}^{2}+{[N-(-N\left)\right]}^{2}}} (8) 利用熵值法,确定“极端情感”与“群体情感”两类样本在“总人数占比”和“情感偏离程度”两项指标上的比重,并构建决策矩阵
\boldsymbol{P}_{ }^t ,公式为{{\boldsymbol{P}}}^{{\boldsymbol{t}}}=\left[\begin{array}{cc}\frac{m}{n}& 1-{E}_{dis}^{t}\\ \frac{n-m}{n}& {E}_{dis}^{t}\end{array}\right] (9) 通过第j 项指标下第i 类样本占该指标的比重ptij(i=1,2;j=1,2),即可分别计算极端情感和群体情感倾向在情感氛围场构建中占有的权重
{Z}_{ext}^{t} 和{Z}_{group}^{t} 。公式为{e}_{j}^{t}=-\frac{1}{\mathrm{l}\mathrm{n}2}\sum_{i=1}^{2}({P}_{ij}^{t}\cdot \mathrm{l}\mathrm{n}({P}_{ij}^{t}\left)\right) (10) {d}_{j}^{t}=1-{e}_{j}^{t} (11) {w}_{j}^{t}=\frac{{d}_{j}^{t}}{\displaystyle\sum_{j=1}^{2}{d}_{j}^{t}} (12) \left[{Z}_{ext}^{t},{Z}_{group}^{t}\right]={w}^{t}\cdot {P}^{t} (13) 公式(10)~(13)中,
{e}_{j}^{t} 为总人数占比和情感偏离程度两项指标的熵值;{e}_{j}^{t} 和{w}_{j}^{t} 为对应的差异系数和估计权重。根据权重
{Z}_{ext}^{t} 和{Z}_{group}^{t} ,可计算得到当存在极端情感个体时的群体情感氛围模型的最终形式{{\boldsymbol{A}}}^{t}=\left[{A}_{val}^{t},{A}_{arl}^{t}\right] ,具体公式为A_{val}^t=Z_{ext}^t\cdot E_{ext,val}^t+Z_{group}^t\cdot G_{val}^t (14) A_{arl}^t=Z_{ext}^t\cdot E_{ext,arl}^t+Z_{group}^t\cdot G_{arl}^t (15) 对式(7)中函数
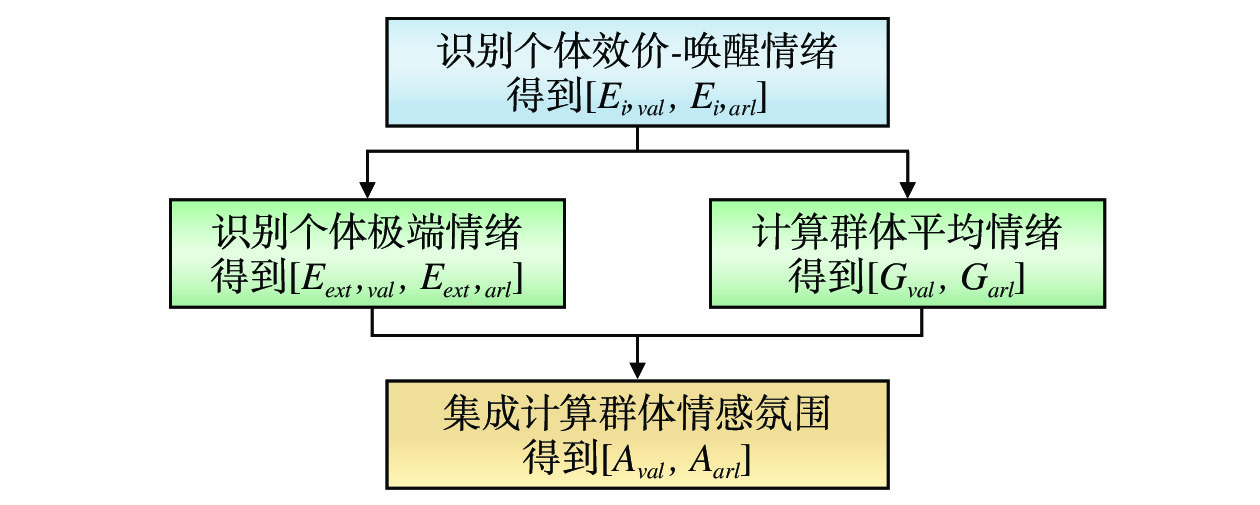
f 进行具体化,本文所提群体情感氛围分析模型的数学表达式为\boldsymbol{A}^t=\left\{\begin{array}{cc}\left[A_{val}^t,A_{arl}^t\right] & ,\mathrm{存}\mathrm{在}\mathrm{极}\mathrm{端}\mathrm{情}\mathrm{感}\mathrm{个}\mathrm{体} \\ \boldsymbol{G}^t & ,\mathrm{不}\mathrm{存}\mathrm{在}\mathrm{极}\mathrm{端}\mathrm{情}\mathrm{感}\mathrm{个}\mathrm{体}\end{array}\right. (16) 群体情感氛围分析算法如图2所示。
2 基于群体情感氛围分析的应急决策方法
在群体情感氛围分析算法的基础上,本章节设计用于铁路客运场所中突发事件的风险等级估计模型及应急决策方法。建立旅客群体情感与应急预案的映射,保证应急决策方法能够满足预防为主、分级管理、快速反应的应急预案工作原则。
2.1 风险等级估计模型的建立
在铁路客运场所,应关注消极效价状态与高唤醒状态,即
{A}_{val} < 0 ,与\left|{A}_{arl}\right|\to N 的情况。基于此,本文给出突发事件风险risk 的估计函数的基本形式为risk=\left\{\begin{array}{ll}\begin{array}{ll}0 \\ g(\left|A_{val}\right|,\left|A_{arl}\right|)\end{array} & \begin{array}{c},\ A_{val}^{ } > 0 \\ ,\ A_{val}^{ }\le0\end{array}\end{array}\right. (17) 式(17)中,
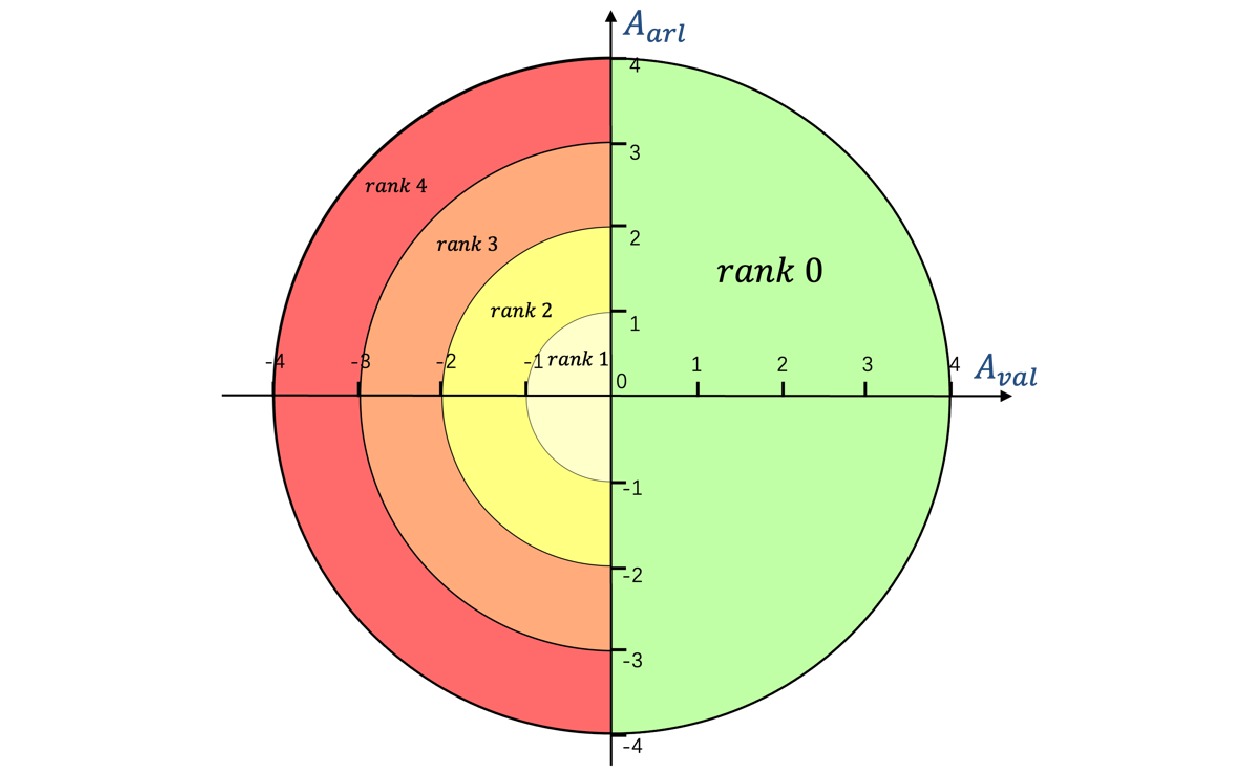
g 是关于\left|{A}_{val}\right| 和\left|{A}_{arl}\right| 的二元函数,且满足\frac{\partial risk}{\partial \left|{A}_{val}\right|} >0,\frac{\partial risk}{\partial \left|{A}_{arl}\right|} >0;{A}_{val} 与{A}_{arl} 的定义域为[-N,N] ,\text{risk} 的值域为[0,N] 。在不同场景中,可根据实际需求修改g 的具体函数,下面对本文g函数展开说明。本文根据群体情感氛围估计结果,设计的室内风险等级估计模型如图3所示。该模型呈环状结构,基于不同效价−唤醒双维度下的群体情感氛围估计风险等级。
根据室内风险等级估计模型,得到用于室内风险等级估计的函数g,
g=\left\lceil { \sqrt{{{A}_{val}^{}}^{2}+{{A}_{arl}^{}}^{2}} } \right\rceil 。因此,室内风险等级估计公式为rank=\left\{\begin{array}{ll}0& , {A}_{val}^{} > 0\\ \left\lceil {\sqrt{{{A}_{val}^{}}^{2}+{{A}_{arl}^{}}^{2}}} \right\rceil & , {A}_{val}^{}\le 0\end{array}\right. (18) 由
{A}_{val}\in [-N,N] ,{A}_{arl}\in [-N,N] 可知,rank\in \mathrm{0,1},\cdots , N 。即风险等级估计模型可将群体情感结果映射为0至N 的风险等级估计输出。2.2 应急决策方法
在应急决策中,本文使用分层级的应急决策方法。分层级的应急决策方案具有整体性、层次性和动态性的优点,同时与自动化的风险等级估计具有良好的适配性。
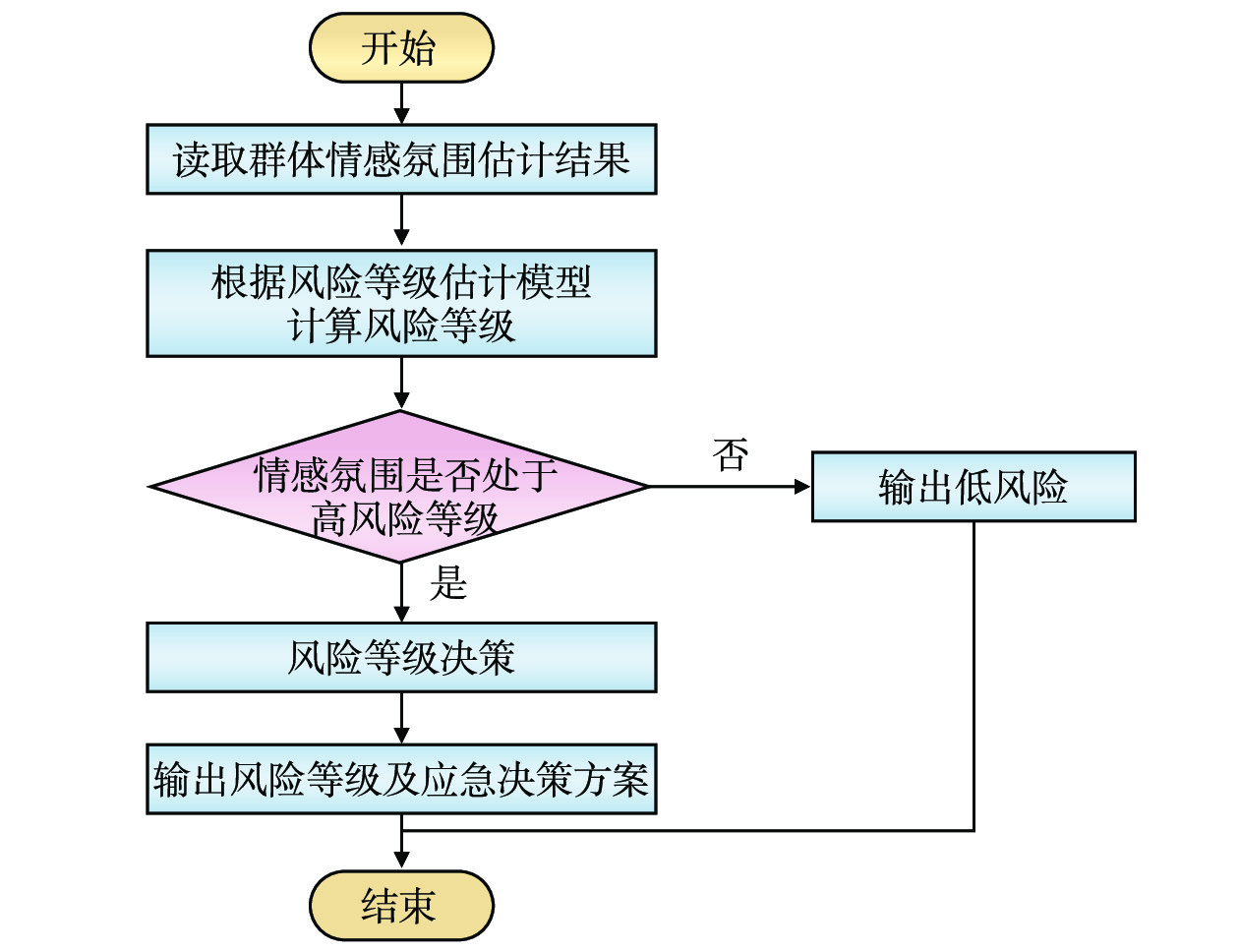
基于群体情感氛围分析的应急决策方法实施流程如图4所示,可根据当前群体情感氛围得到实时的风险等级,并自动调用相应的应急预案。
为使本方法能够根据各风险等级及时发布有效信息,快速进行各项预防和应对处置工作[13],风险等级估计模型应提供准确的等级输出。针对风险等级的不同输出,调用不同的应急决策方案。根据公式(16),群体情感氛围映射为
rank\in \mathrm{0,1},2,\cdots ,N ,刨除低风险(rank=0),即可实现群体情感氛围与0至N 级(N 可根据具体场景设置)的应急预案间的映射。参考《国家处置铁路行车事故应急预案》中对应急响应级别的分级,根据铁路行车事故的可控性、严重程度和影响范围等因素,将应急响应级别分为Ⅰ、Ⅱ、Ⅲ、Ⅳ级,分别对应特别重大、重大、较大和一般4个级别的铁路突发事件。因此,在客运公共场所安全保障应急预案体系中,我们将突发事件风险等级分为0至4级,分别对应低风险、一般、较大、重大、特别重大5类级别的铁路突发事件。风险等级及对应的应急预案如表1所示。
表 1 风险等级及对应的应急预案风险层级 应急预案(例) 0级(低风险) 一切正常 1级(一般)
例:列车延误导致旅客烦躁向监控室及安保巡查人员进行内部提示;
现场广播:“请广大旅客注意安全有序候车”。2级(较大)
例:有旅客在候车大厅发生口角向监控室进行警报,要求安保巡查人员赶往现场处理;
现场广播:“请有需要的乘客等待工作人员上前处理”。3级(重大)
例:候车排队出现多人纠纷冲突向监控室及安保巡查人员进行警报,并通知相邻节点执勤人员;
从相邻节点执勤人员中调派10人赶往现场进行处理;
现场广播:“请旅客有序疏散”。4级(特别重大)
例:发生群体性打斗事件向监控室及安保巡查人员进行警报,并通知相邻节点执勤人员;
从相邻节点执勤人员中调派20人赶往现场控制局面;
现场广播:“请旅客有序疏散”;
并报警,等待警察到场处理。基于本文的应急决策方法,不仅可在识别到具体异常事件后给出报警,更可在出现集体性的群体情感波动时及时通知相关工作人员,引起重视,在风险事件发生前通过广播或工作人员早期干预,降低风险实际发生的可能性。根据实际使用需求与管理要求,风险等级的数量及应急决策方案的具体内容均可进行调节。
3 实验及分析
为验证本文方法的有效性,设计了2个实验,进行群体情感氛围的估计与风险等级估计。利用IEMOCAP公开数据集中的双人对话视频[14],通过截取多个5 s的片段,提取连续情感标签中的效价和唤醒维度,计算个体情感,并融合为群体情感氛围;使用自然场景下多人争吵或肢体冲突的视频,进一步验证在复杂场景下群体情感氛围计算与分析模型和风险等级估计模型的有效性。
3.1 实验室场景的群体情感氛围实验
本实验基于截取的IEMOCAP 公开数据集中双人场景下的视频画面。IEMOCAP 公开数据集是一个交互式情感二元运动捕捉数据集,包含大约 12 h的视听数据,提供了视频、音频、文本转录、动作捕捉等模态的数据信息,由 10 余名专业演员以即兴对话形式录制而成。IEMOCAP 公开数据集采用离散情感标签和连续情感标签进行标注,每个语句片段均由至少3名情感估计员对相应的情感类型进行估计。连续情感标签从效价维度和唤醒维度对演员情感进行估计,本文使用连续情感标签的效价和唤醒维度作为标签,并将原始数据映射到{−3,−2,−1,0,1,2,3}的整数标签,以便搭建情感模型。
本文选择20个包含对话的视频,其中10个视频中2人均为平静或积极情感状态(编号1~10),其余10个视频中至少1人处于极端负面情感(编号11~20)。对每个视频随机截取5 s(25帧)作为1个测试样本。实验结果如表2所示。
表 2 实验室场景群体情感氛围及风险等级估计实验结果实验编号 个体1情感 个体2情感 平均情感 \boldsymbol{G} 群体情感氛围 \boldsymbol{A} 依据平均情感的风险等级预估 依据群体情感氛围的风险等级预估 1 (3,1) (1,2) (2,1.5) (2,1.5) 0 0 2 (3,0) (1,1) (2,0.5) (2,0.5) 0 0 3 (1,0) (0,0) (0.5,0) (0.5,0) 0 0 4 (2,3) (0,1) (1,2) (1,2) 0 0 5 (−1,1) (0,2) (−0.5,1.5) (−0.5,1.5) 1 1 6 (−1,0) (2,0) (0.5,0) (0.5,0) 0 0 7 (1,−2) (1,1) (1,−0.5) (1,−0.5) 0 0 8 (2,−3) (1,−1) (1.5,−2) (1.5,−2) 0 0 9 (0,0) (0,1) (0,0.5) (0,0.5) 0 0 10 (2,1) (3,2) (2.5,1.5) (2.5,1.5) 0 0 11 (−2,1) (−1,−1) (−1.5,0) (−1.75,0.5) 1 1 12 (−1,3) (2,3) (0.5,3) (−0.25,3) 0 3 13 (−1,−2) (1,1) (0,−0.5) (−0.5,−1.25) 0 1 14 (−2,−2) (3,−2) (0.5,−2) (−0.75,−2) 0 2 15 (−3,−3) (−1,−1) (−2,−2) (−2.5,−2.5) 2 3 16 (−3,3) (−1,0) (−2,1.5) (−2.5,2.25) 2 3 17 (−1,3) (0,2) (−0.5,2.5) (−0.75,2.75) 2 2 18 (−2,−2) (−2,−1) (−2,−1.5) (−2,−1.5) 2 2 19 (−1,2) (−1,3) (−1,2.5) (−1,2.5) 2 2 20 (−2,1) (−3,−3) (−2.5,−1) (−2.5,−1) 2 2 表2中,平均情感列展示了基于公式(5)和(6)计算得到的平均情感;群体情感氛围列则为使用本文方法计算的群体情感氛围值。最右两列分别为仅使用平均情感
\boldsymbol{G} 计算得到的预估风险等级和使用群体情感氛围\boldsymbol{A\boldsymbol{ }} 计算得到的预估风险等级。可看出,在有至少1人处于极端情感状态时(实验编号为12~16的实验结果),本文方法可更好捕捉到群体中发生的异常情感状态,并提高风险等级(橙色区域),从而给出预警。实验编号11的群体情感氛围估计如图5所示。图5中,左侧女性
P 情感较为激动,右侧男性Q 情感相对平稳。黑色圆点分别代表两人的个体情感,黄色圆点为两人的平均情感\boldsymbol{G}^t ,红色圆点为群体情感氛围\boldsymbol{A}^t 。可看出,红色圆点显示的情感氛围估计结果相对群体情感估计结果向低效价-高唤醒区域倾斜。实验结果表明,本文方法可在多人场景下,更好地检测群体情感氛围,并在有极端情感个体时给出更合理的群体情感融合结果。3.2 自然场景的群体情感氛围实验
自然场景下的群体情感氛围实验选择了2段含有激烈争吵或肢体冲突的不同视频片段进行拼接,拼接后片段长2 min,如图6所示。在35 s(图6(a))和100 s(图6(c))时人群中有打斗,在70 s(图6(b))时人群中有明显争吵,在110 s(图6(d))时冲突结束。
对以上视频以3 s为1小节,进行分别识别。表情及姿态模态提取帧率为 5 Fps,1小节总帧数为15帧;音频模态提取帧率为
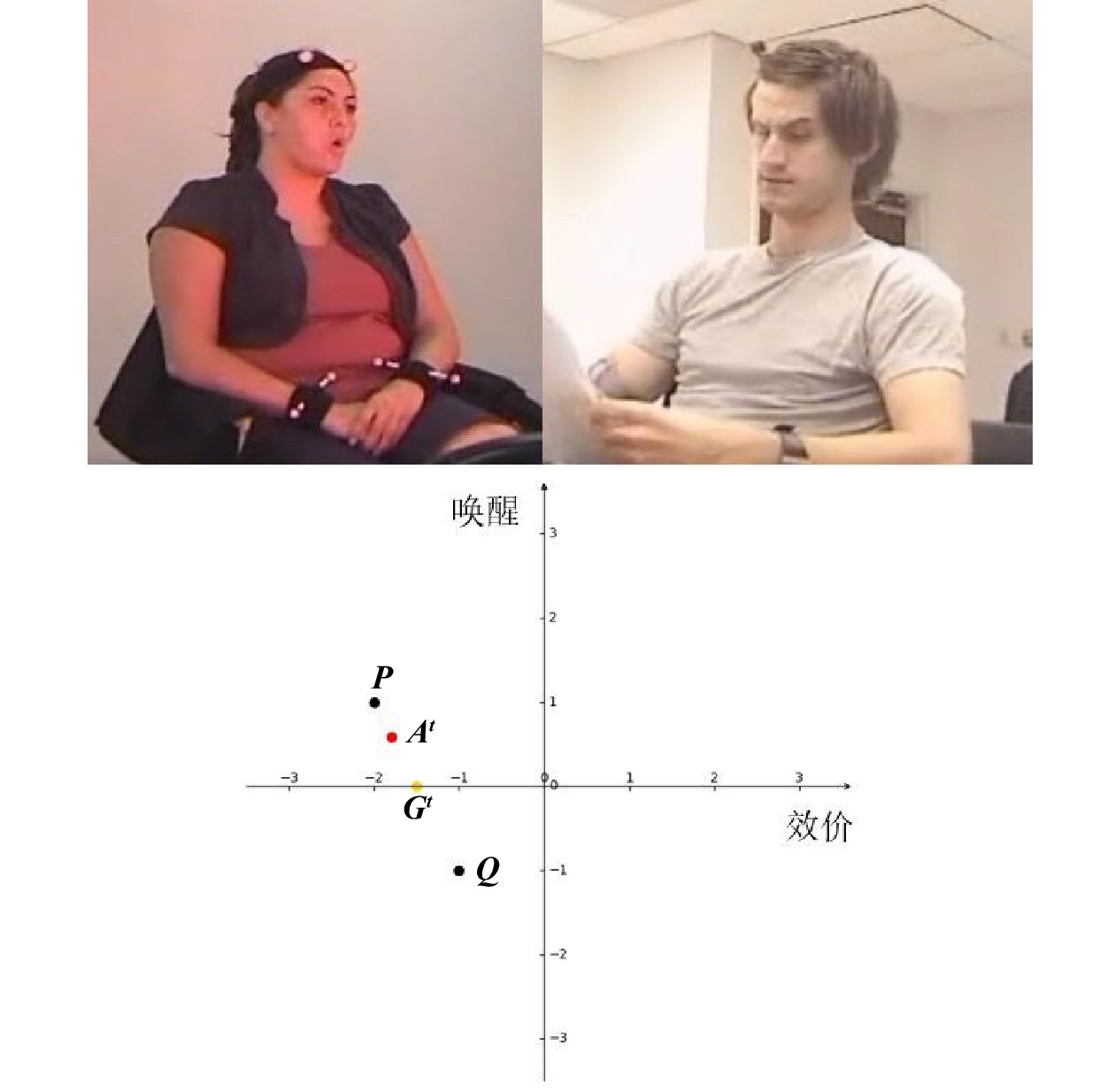
8000 Fps,1小节总帧数24000 帧。按照每小节中显示的情感强烈程度,在效价和唤醒维度上对视频小段进行标注,标签与 IEMOCAP 公开数据集一致。对影视片段进行测试,共计 600 帧,绘制单帧条件下,效价和唤醒维度下的群体情感倾向和情感氛围估计结果随帧数变化的折线图如图7所示。由图7可看出,由于选择了包含多人争吵打斗的场景,人群长时间处于低效价状态(情感消极),且唤醒维度上具有较大波动。效价在35 s左右和100 s左右降至最低点(红色部分),表示人群群体情感氛围极端消极,与图6中展示的打斗极端行为相吻合;70 s时效价较低、唤醒较低(黄色部分),与人群中有不满情感但尚未发生风险事件的情形吻合;110 s效价与唤醒均趋近于0(绿色部分),与事态得到控制相吻合。因此,折线图反映的群体情感氛围与显示场景具有一致性。
对于效价维度上的情感氛围估计结果,极端情感的存在会使估计结果向负向区域倾斜。对于群体情感倾向偏中性或积极状态时,少量极端情感的存在会使情感氛围估计结果向负半区移动;而当群体情感倾向已经位于极端范畴时,极端情感的存在对情感氛围估计结果影响不大。由效价和唤醒维度折线图进行对比可以看出,对于群体情感倾向和情感氛围估计结果有较大差异的区域,即极端情感在情感氛围估计结果中占有较大比重,在后续的时间段中,群体情感倾向也趋于极端范畴。因此,对个体极端情感的判定有助于群体情感氛围演变态势的描述。
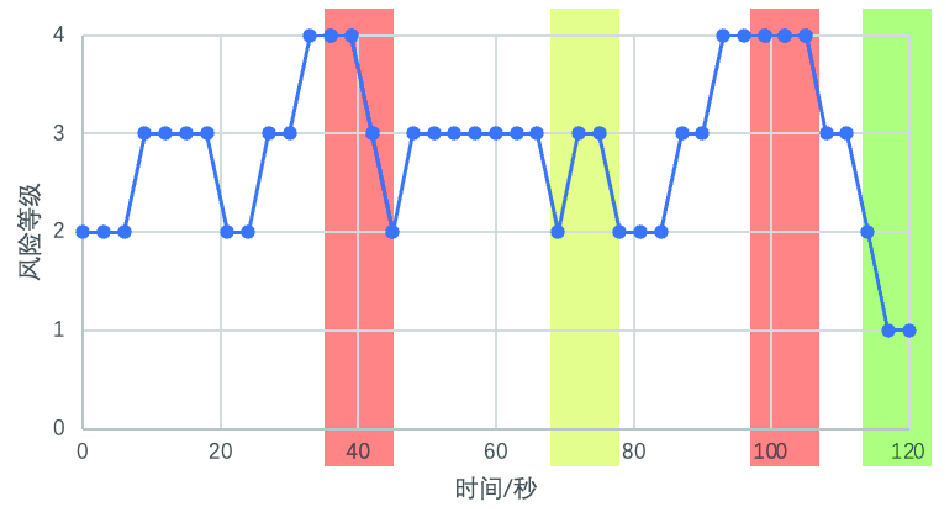
进一步的,根据效价和唤醒维度下的情感氛围估计结果绘制风险等级折线图,如图8所示。
该实验选取视频的风险等级基本处于等级2至等级3之间,当人群出现激烈争吵或打斗情况时(图8红色区域),风险等级上升至等级4;当人群得到控制后(图8绿色区域),风险等级降为等级1。决策结果可较为准确地反映视频中发生的风险事件。
4 结束语
本文提出的基于群体情感氛围智能计算的应急决策分析方法,实现了对铁路客运场所潜在安全风险的早期识别与应急响应。通过情感效价−唤醒模型和熵值法量化模型,建立多人场景下的群体情感氛围分析模型,实时分析客运场所内旅客的群体情感状态,并提供相应的风险等级估计与应急决策。
在IEMOCAP公开数据集与自制多人自然场景数据集的实验验证结果表明,所提出的算法可识别群体极端情感变化,研究具有实用性。未来工作将进一步优化方法的预测精度,并探索其在更多应用场景下的潜力。
-
表 1 风险等级及对应的应急预案
风险层级 应急预案(例) 0级(低风险) 一切正常 1级(一般)
例:列车延误导致旅客烦躁向监控室及安保巡查人员进行内部提示;
现场广播:“请广大旅客注意安全有序候车”。2级(较大)
例:有旅客在候车大厅发生口角向监控室进行警报,要求安保巡查人员赶往现场处理;
现场广播:“请有需要的乘客等待工作人员上前处理”。3级(重大)
例:候车排队出现多人纠纷冲突向监控室及安保巡查人员进行警报,并通知相邻节点执勤人员;
从相邻节点执勤人员中调派10人赶往现场进行处理;
现场广播:“请旅客有序疏散”。4级(特别重大)
例:发生群体性打斗事件向监控室及安保巡查人员进行警报,并通知相邻节点执勤人员;
从相邻节点执勤人员中调派20人赶往现场控制局面;
现场广播:“请旅客有序疏散”;
并报警,等待警察到场处理。表 2 实验室场景群体情感氛围及风险等级估计实验结果
实验编号 个体1情感 个体2情感 平均情感 \boldsymbol{G} 群体情感氛围 \boldsymbol{A} 依据平均情感的风险等级预估 依据群体情感氛围的风险等级预估 1 (3,1) (1,2) (2,1.5) (2,1.5) 0 0 2 (3,0) (1,1) (2,0.5) (2,0.5) 0 0 3 (1,0) (0,0) (0.5,0) (0.5,0) 0 0 4 (2,3) (0,1) (1,2) (1,2) 0 0 5 (−1,1) (0,2) (−0.5,1.5) (−0.5,1.5) 1 1 6 (−1,0) (2,0) (0.5,0) (0.5,0) 0 0 7 (1,−2) (1,1) (1,−0.5) (1,−0.5) 0 0 8 (2,−3) (1,−1) (1.5,−2) (1.5,−2) 0 0 9 (0,0) (0,1) (0,0.5) (0,0.5) 0 0 10 (2,1) (3,2) (2.5,1.5) (2.5,1.5) 0 0 11 (−2,1) (−1,−1) (−1.5,0) (−1.75,0.5) 1 1 12 (−1,3) (2,3) (0.5,3) (−0.25,3) 0 3 13 (−1,−2) (1,1) (0,−0.5) (−0.5,−1.25) 0 1 14 (−2,−2) (3,−2) (0.5,−2) (−0.75,−2) 0 2 15 (−3,−3) (−1,−1) (−2,−2) (−2.5,−2.5) 2 3 16 (−3,3) (−1,0) (−2,1.5) (−2.5,2.25) 2 3 17 (−1,3) (0,2) (−0.5,2.5) (−0.75,2.75) 2 2 18 (−2,−2) (−2,−1) (−2,−1.5) (−2,−1.5) 2 2 19 (−1,2) (−1,3) (−1,2.5) (−1,2.5) 2 2 20 (−2,1) (−3,−3) (−2.5,−1) (−2.5,−1) 2 2 -
[1] 刘振芳. 全面深化改革创新 奋力推动铁路高质量发展 为服务和支撑中国式现代化作出更大贡献——在中国国家铁路集团有限公司工作会议上的报告(摘要)[J]. 铁路计算机应用,2024,33(1):1-8. [2] 汪 玚. 共绘“新质”蓝图——专家热议加强科技引领助力发展交通运输新质生产力[J]. 交通建设与管理,2024(2):24-27. [3] Narayanan M, Jaju S, Nair A, et al. Real-time video surveillance system for detecting malicious actions and weapons in public spaces[C]//Proceedings of the Third ICCNCT 2020 on Computer Networks and Inventive Communication Technologies, 23-24 July, 2020, Berlin Heidelberg: Springer, 2021. 153-166.
[4] Zouaoui R, Audigier R, Ambellouis S, et al. Embedded security system for multi-modal surveillance in a railway carriage[C]//Proceedings of the SPIE 9652, Optics and Photonics for Counterterrorism, Crime Fighting, and Defence XI, 21-24 September, 2015, SPIE, 9652C.
[5] Garzia F, Borghini F, Castagnolo A, et al. Emotional analysis of safeness and risk perception of drones during the COVID-19 pandemic in Italy[C]//Proceedings of 2020 International Carnahan Conference on Security Technology, 11-15 October, 2021, New York, USA: IEEE, 2021. 1-6.
[6] 张宇开. 基于BS模式的网络舆情安全监控系统设计与实现[D]. 西安:西安电子科技大学,2020. [7] Dai Y, Liu X Y, Dong S Z, et al. Group emotion recognition based on global and local features[J]. IEEE Access, 2019(7): 111617-111624. DOI: 10.1109/ACCESS.2019.2932797
[8] Hou R K, Xu X Y, Dai Y P, et al. A multimodal fusion behaviors estimation method for public dangerous monitoring[J]. Journal of Advanced Computational Intelligence and Intelligent Informatics, 2024, 28(3): 520-527. DOI: 10.20965/jaciii.2024.p0520
[9] 向良云. 重大群体性事件演化升级的影响因素分析——基于扎根理论方法的研究[J]. 情报杂志,2012,31(4):64-69. [10] Kuppens P, Tuerlinckx F, Russell J A, et al. The relation between valence and arousal in subjective experience[J]. Psychological bulletin, 2013, 139(4): 917-940. DOI: 10.1037/a0030811
[11] 戴亚平,陈奕杉,廖天睿,等. 基于多级长短期记忆网络的多模态情感应急决策系统:CN,115393927A[P]. 2022-11-25. [12] Ding X W, Chong X, Bao Z F, et al. Fuzzy comprehensive assessment method based on the entropy weight method and its application in the water environmental safety evaluation of the Heshangshan drinking water source area, three gorges reservoir area, China[J]. Water, 2017, 9(5): 329. DOI: 10.3390/w9050329
[13] 刘阳学,段卿培,蒋丽丽,等. 铁路时空大数据应急辅助决策系统及关键技术[J]. 铁路计算机应用,2021,30(10):19-23. DOI: 10.3969/j.issn.1005-8451.2021.10.05 [14] Busso C, Bulut M, Lee C C, et al. IEMOCAP: interactive emotional dyadic motion capture database[J]. Language Resources and Evaluation, 2008, 42(4): 335-359. DOI: 10.1007/s10579-008-9076-6




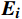
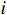
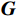
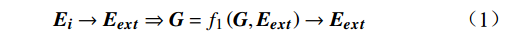
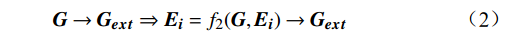
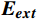
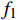
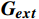
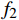
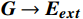
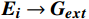
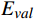
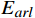
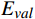
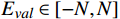
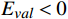
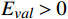
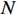
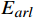
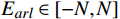
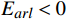
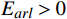
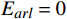
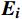
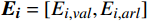
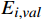
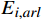
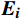
 下载:
下载: