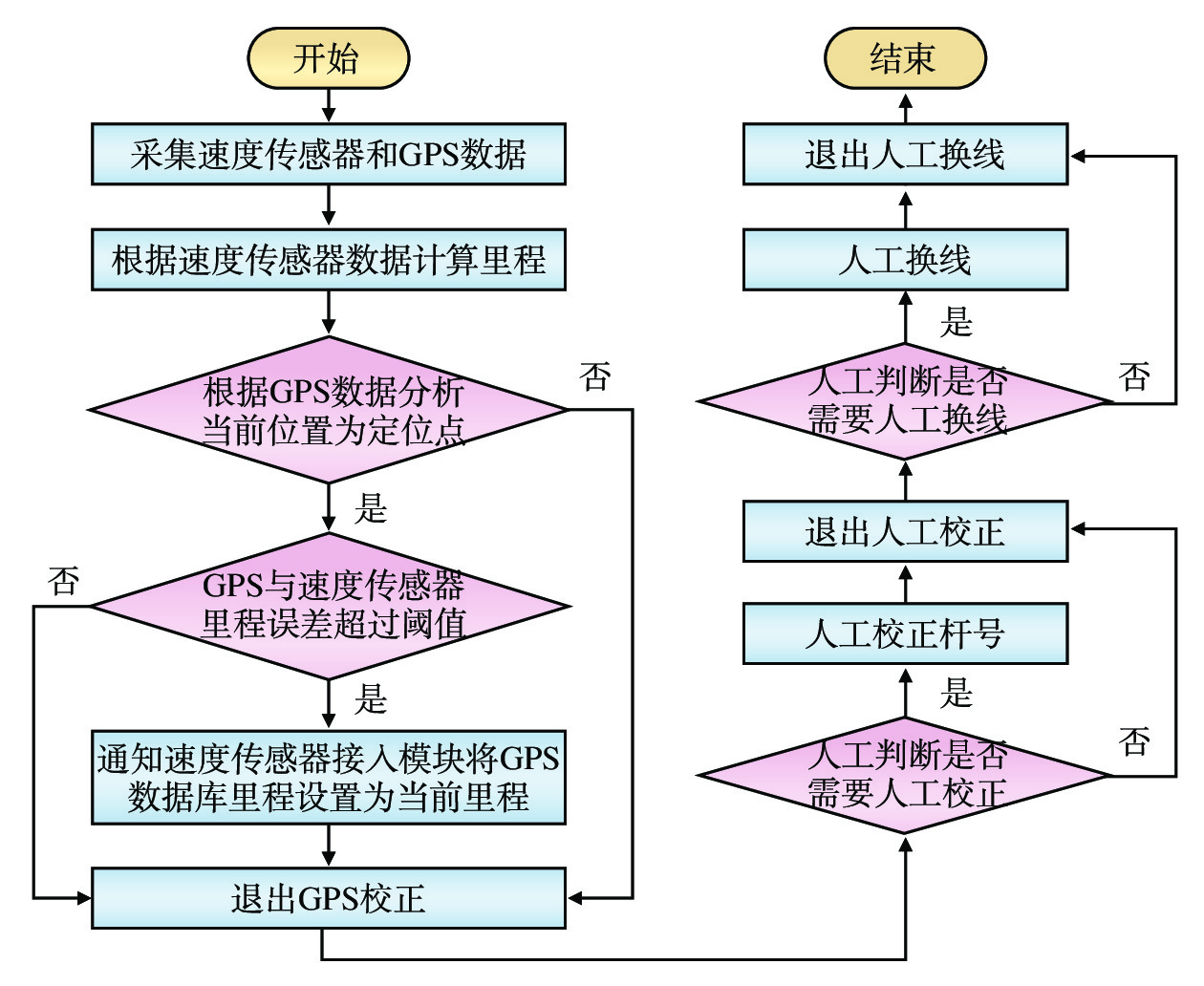
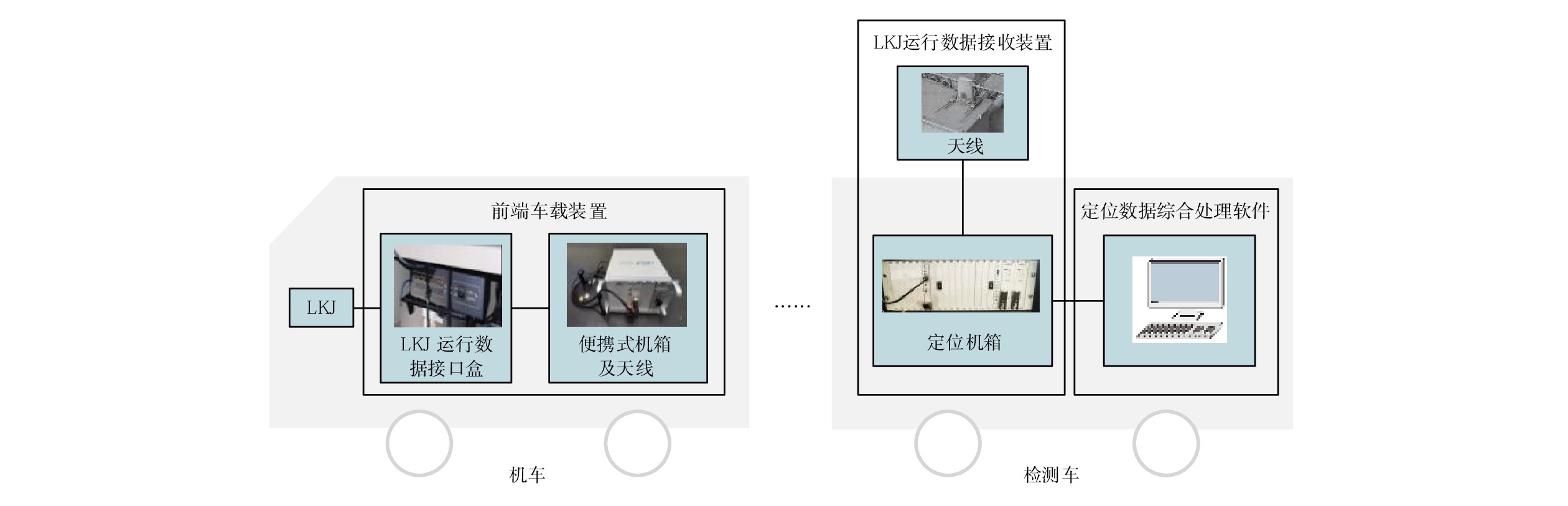
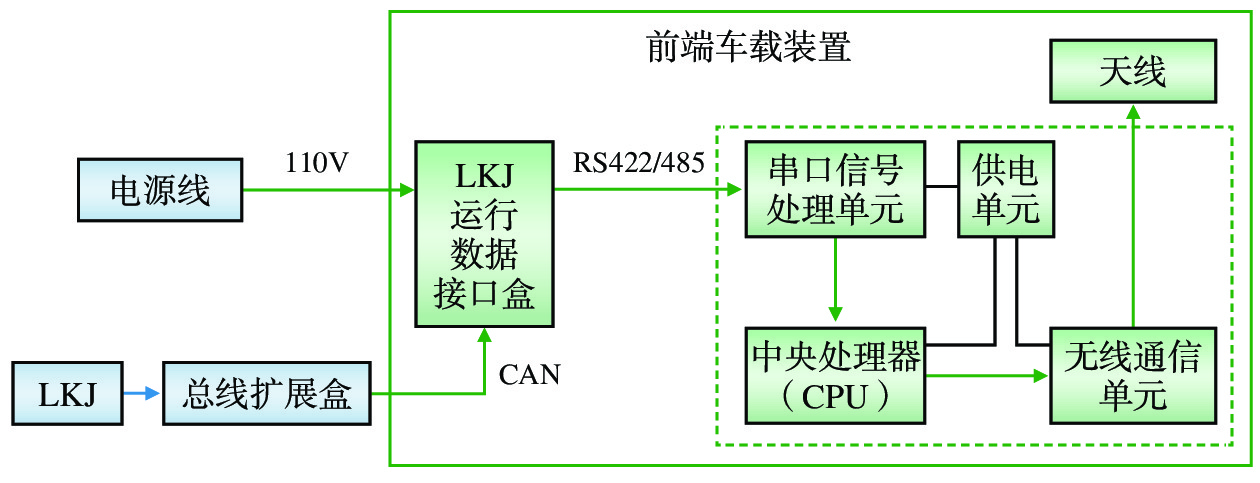
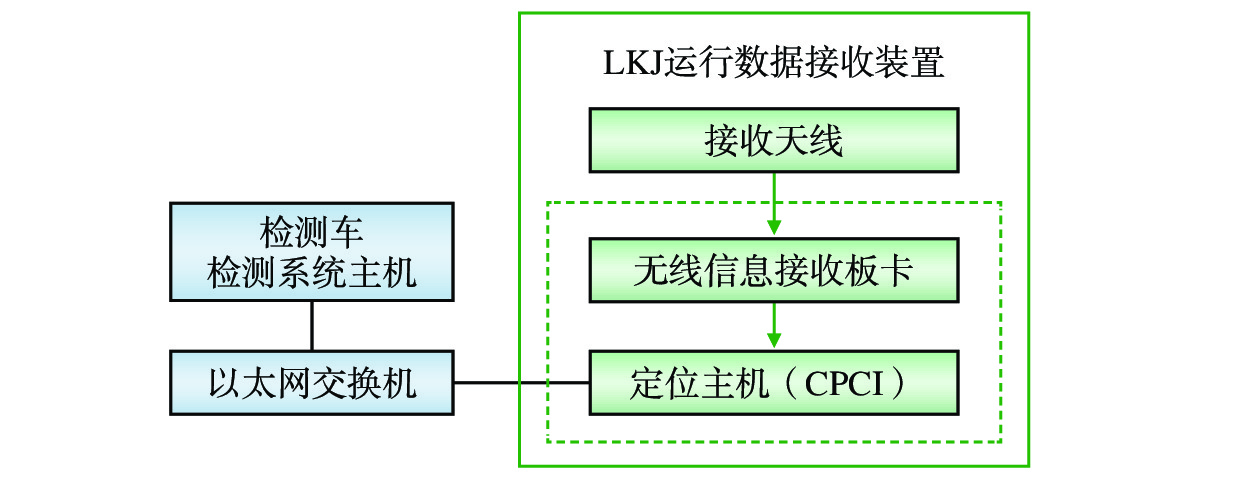
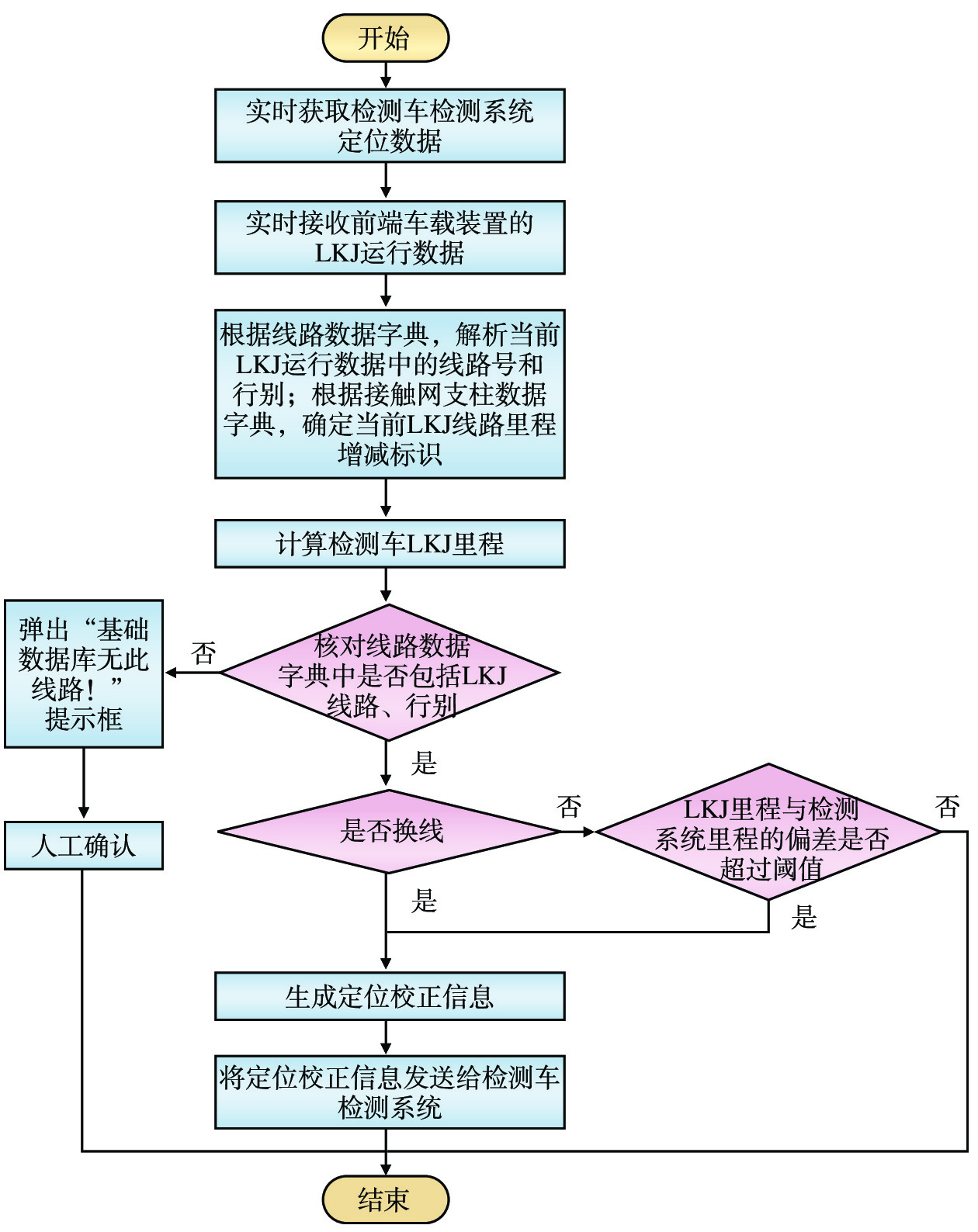
Research on general-purpose automatic position rectification equipment based on LKJ operation data for railway infrastructure inspection cars
-
摘要:
中国铁路成都局集团有限公司(简称:成都局)山区铁路隧道多、枢纽线路复杂,基础设施检测车定位精准度不高,全球定位系统(GPS,Global Positioning System)信号无法全程提供里程校正,人工校正和换线操作繁琐费力。文章提出基于列车运行监控记录装置(LKJ)运行数据的铁路基础设施检测车通用定位自动校正设备的设计,由安装在机车上的前端车载装置、安装在检测车上的 LKJ 运行数据接收装置和定位数据综合处理软件组成;能够实时获取LKJ运行数据,通过无线通信传输至检测车,自动完成线路转换和里程校正,为检测车提供较为精准的定位校正信息。该设备适用于成都局配属的各专业基础设施检测车,安装简单快捷,与LKJ装置的接口具备完善的电气隔离。目前,该设备已在成都局电务检测车和接触网检测车上开展初步动态测试,基本达到设计要求,提升了基础设施检测车的智能化程度,有助于提高检测作业质量和效率。
-
关键词:
- 基础设施检测车 /
- 列车运行监控记录装置(LKJ) /
- 精准定位 /
- 自动里程校正 /
- 自动线路转换
Abstract:China Railway Chengdu Bureau Group Co., Ltd. (referred to as Chengdu Bureau) has many railway tunnels in mountainous areas and complex lines within the hubs. The infrastructure inspection cars have some common problems such as low positioning accuracy, inability to provide effective mileage rectification with GPS signals throughout the whole inspection process, tedious and laborious operations of manual mileage rectification and line changing. The article proposes a design of a general-purpose automatic position rectification equipment for railway infrastructure inspection cars based on ocomotive LKJ operation data. The equipment consists of a front-end onboard device installed on the locomotive, an LKJ operation data receiving device installed on the inspection car, and a suite of comprehensive positioning data processing software. The equipment can obtain real-time operation data from the locomotive 's LKJ equipment, transmit it to the inspection car via wireless communication, complete line changing and mileage correction automatically and provide precise position rectification data for the inspection car. This equipment is suitable for various specialty infrastructure inspection cars assigned by Chengdu Bureau, and easy and fast to install. At present, the equipment has undergone preliminary dynamic testing on one signal and comminications inspection car and one OCS inspection car, basically meeting the design requirements, improving the intelligence level of infrastructure inspection cars, and helping to improve the quality and efficiency of inspection operations.
-
截至2024年底,我国高速铁路(简称:高铁)运营里程已超过4.8万km[1],铁路已成为我国现代交通体系的核心组成部分。然而,随着铁路建设规模的扩大和运行速度的提高,铁路基础设施的安全性和稳定性问题日益凸显[2]。作为轨道结构的基础,路基沉降不仅会导致轨道几何形位超限,引发列车运行振动加剧、维护成本增加等问题,甚至会威胁行车安全。铁路路基沉降探测波长预测是服务于沉降预测的技术手段,波长预测的合理性直接影响探测数据的质量,进而影响后续沉降预测的准确性。因此,合理的波长预测模型是精准预测路基沉降的重要技术支撑,对保障线路平顺性、提升运营安全与效率具有重要意义。
传统的路基沉降预测方法,如双曲线法[3]、指数曲线法[4]和Asaoka法[5]等,虽在一定程度上发挥了作用,但在处理复杂、多因素和非线性的铁路路基沉降过程时,存在精度不足和适应性差的问题。近年来,机器学习算法因其在解决高维非线性问题方面的能力,逐渐被应用于隧道施工沉降预测,如前馈神经网络反向传播算法、人工神经网络法[6]、粒子群优化改进的反向传播(BP,Back Propagation)神经网络[7]及自适应遗传算法等,通过挖掘监测数据内在规律,在不同模型有机组合及先进智能算法应用等方面均取得显著进展。Wenqian Xu等人[8]基于车辆动力响应与一维卷积神经网络1D-CNN( Convolutional Neural Networks),通过多通道车辆加速度数据实现高铁无砟轨道路基沉降的智能识别;Guankai Wang等人[9]提出物理信息神经网络(PINN,Physics-Informed Neural Networks)模型,将盾构隧道施工物理方程与神经网络结合,利用有限监测数据实现路基沉降预测与参数反演,取得了一定成果。但现有模型对复杂多因素耦合作用的建模能力有限,导致预测结果在非线性强、时变特征显著的路基场景中误差较大,难以保证预测结果的可靠性。
为了提高路基沉降预测精度,本文结合实际工程需求,利用光纤传感器传输损耗小、远距离监测、高灵敏性和精准度等优势,融合时间卷积网络(TCN,Temporal Convolutional Network)、Transformer自注意力机制和长短期记忆(LSTM,Long Short-TermMemory)网络等模型,构建基于深度学习的铁路路基沉降探测波长预测模型(简称:本文模型),旨在通过挖掘路基沉降探测波长数据的周期性规律,辨识路基沉降的异常波动趋势,提升路基沉降风险的实时监测与预警能力。
1 预测模型构建
1.1 模型架构设计
融合多种神经网络结构,设计本文模型。采用多模态融合、多层次表征、多尺度感知的设计理念,集成了Transformer自注意力机制、TCN和LSTM网络等3种深度学习架构的优势,使得该该模型能够有效捕捉时间序列数据中的长短期依赖关系和空间—时间特性,以提高对铁路路基沉降波长的预测精度和鲁棒性。
铁路路基沉降探测波长预测模型架构如图1所示。向该模型输入包含时间特征、位置特征和历史波长数据的多维时间序列
X∈RB×T×F ,其中,B 表示批次大小;T 表示序列长度;F 表示特征维度。通过特征嵌入模块将输入映射到高维表征空间E=WeX+be(We∈RF×D,be∈RD) ,其中,D表示嵌入维度。随后,位置编码模块为序列数据注入位置信息,使该模型能够感知数据的时序关系。在深层特征提取阶段,该模型通过自注意力模块捕获序列内部的全局依赖关系;通过TCN模块提取多尺度时间模式;通过序列记忆模块获取序列的上下文信息;最终,通过多头注意力模块对提取的特征进行加权整合,并由全连接层生成未来多个时间步的波长预测值Y∈RB×P ,其中,P 表示预测步长。1.2 数据预处理
本文采用标准化预处理方法,对时间特征、位置特征和波长特征分别进行归一化处理,以消除量纲差异,加速模型收敛。标准化预处理公式为
x′=x−μω (1) 式(1)中,
μ 和ω 分别表示特征的均值和标准差。针对时间特征,本文采用时间编码方式,将原始时间戳转换为一天内的相对时间,转换公式为timeofday=hour×3 600+minute×60+second86 400 (2) 这种编码方式保留了时间的周期性特征,有助于模型捕捉与时间相关的模式。
此外,针对异常值和离群点,本文设计了基于四分位距(IQR,Interquartile Range)和Z-score的检测与处理策略。IQR方法的异常值判定标准为
x<Q1−2×IQR或x>Q3+2×IQR (3) 式(3)中,
Q1 、Q3 分别表示第一四分位数和第三四分位数;四分位距IQR=Q3−Q1 。对于检测到的异常值,采用移动中位数替换方法进行平滑处理,提高数据质量。1.3 关键组件实现
1.3.1 位置编码模块
路基沉降数据具有明显的时序特性,为使本文模型能够感知输入序列中各元素的相对位置关系,本文采用正弦余弦位置编码方法,其位置编码计算公式为
PE(pos,2i)=sin(pos10 0002i/dmodel) (4) PE(pos,2i+1)=cos(pos10 0002i/dmodel) (5) 式(4)~式(5)中,
pos 表示序列中的位置索引,i 表示维度索引;PE(pos,2i) 表示位置pos 偶数维度2i 对应的正弦位置编码;PE(pos,2i+1) 表示位置pos 奇数维度2i+1 偶数维度对应的余弦位置编码;dmodel 表示嵌入维度。这种编码方式的优势包括:(1)每个位置对应的编码唯一,确保了不同位置的可区分性;(2)相对位置关系被隐式地编码在向量的内积中,使得本文模型能够学习到不同位置间的关系;(3)该编码方法可扩展到未见过的序列长度,提高了本文模型的泛化能力。位置编码矩阵
PE∈RTmax 被添加到输入嵌入中,公式为{H_1} = {H_0} + P{E_{[:{T_{\max }},:]}} (6) 式(6)中,
{H_1} 表示最终嵌入;{H_0} 为特征嵌入;P{E_{[:{T_{\max }},:]}} 表示位置编码;{T_{\max }} 为预设的最大序列长度。该操作使得序列中的每个元素都包含了其位置信息,为后续的自注意力计算提供了序列中每个元素在时间维度或位置维度上的相对关系信息。1.3.2 自注意力模块
路基沉降波长时间序列中存在长距离依赖关系和复杂的时变模式,传统的循环神经网络难以有效建模。因此,本文模型采用基于Transformer架构的自注意力机制,能够直接建立序列中任意两个时间点间的关联,有效捕获全局依赖关系。
多头自注意力计算过程可表示为
\begin{gathered} Attention(Q,K,V) = softmax \left( \frac{{Q{K^T}}}{{\sqrt {{d_k}} }} \right)V \\ \end{gathered} (7) \begin{gathered} hea{d_i} = Attention(QW_i^Q, KW_i^K,VW_i^V) \\ \end{gathered} (8) \begin{gathered} MultAttention(Q,K,V) = Con - \\ cat(hea{d_1},hea{d_2},\cdots,hea{d_h}){W^O} \\ \end{gathered} (9) 式(7)~式(9)中,
Attention(Q,K,V) 表示注意力机制的输出;Q 、K 、V 分别表示查询、键和值矩阵,由输入特征通过线性变换得到;{d_k} 表示键向量的维度;soft{max}(·) 为归一化指数函数,对矩阵每一行进行归一化;hea{d_i} 为第i 个注意力头的输出;W_i^Q 、W_i^K 和W_i^V 是第i 个查询、键和值矩阵的可学习的参数矩阵;MultiAttention(Q,K,V) 表示多头注意力机制的输出;h 为注意力头的数量;Concat(·) 将所有注意力头的输出拼接;{W^O} 是可学习的输出参数矩阵。本文模型采用多个注意力头,每个头学习不同的特征子空间表示,再通过连接操作和线性变换得到综合表示。为提高训练稳定性和模型表达能力,自注意力模块还集成了残差连接、层归一化和前馈神经网络。残差连接和层归一化的组合可表示为
\begin{split} {H_2} =& LayerNorm({H_1} + \\ & Dropout( MultiHead({H_1},{H_1},{H_1}))) \end{split} (10) \begin{gathered} {H_3} = LayerNorm({H_2} + Dropout( FFN({H_2}))) \\ \end{gathered} (11) 式(10)~式(11)中,
{H_2} 表示残差连接和层归一化后的特征;LayerNorm(·) 为层归一化;Dropout(·) 为正则化;{H_3} 为中间特征;FFN 表示由两层线性变换和激活函数组成的前馈神经网络,其公式为FFN(x) = GELU(x{W_1} + {b_1}){W_2} + {b_2} (12) 式(12)中,
FFN(x) 为前馈神经网络的输出;GELU(·) 表示激活函数;{W_1} 、{W_2} 、{b_1} 和{b_1} 为可学习的参数矩阵。本文模型使用GELU 激活函数替代传统的{Re} LU ,提高了对非线性模式的建模能力。1.3.3 TCN模块
为高效提取不同时间尺度上的特征模式,本文模型整合了TCN模块。该模块采用因果卷积结构,确保模型不会利用未来信息进行当前时刻的预测,同时通过膨胀卷积扩大感受野,实现对长序列依赖关系的高效建模。
TCN模块的核心是带有膨胀率的一维卷积操作,其输出可表示为
\begin{array}{l}F(s)=(x{\ast }_{d}f)(s)= {\displaystyle \sum _{i=0}^{k-1}f(i)·x(s-d·i)}\end{array} (13) 式(13)中,
x 是输入序列;f 是卷积核;k 是卷积核尺寸;d 是膨胀率;{ * _d} 表示带有膨胀率d 的卷积操作。本文模型采用指数增长的膨胀率设计,第l 层的膨胀率为{d_l} = {2^l} ,使得本文模型的感受野随网络深度呈指数级增长,有效解决了长序列建模中的梯度问题。TCN模块的输出经过批量归一化和非线性激活函数后,与输入通过残差连接相加,公式为
{H_4} = GELU({H'_3} + {{\mathrm{Re}}} sidual({H_3})) (14) 式(14)中,
{H_4} 为TCN模块的最终输出;{H'_3} 表示经过卷积、批量归一化和激活函数处理后的特征;\mathrm{Re}sidual(·) 表示残差映射,当输入输出维度相同时为恒等映射,否则通过1×1卷积进行维度匹配。1.3.4 序列记忆模块
为进一步增强本文模型对序列的记忆能力和上下文理解,本文模型集成了双向LSTM层。LSTM的门控机制能够选择性地保留和遗忘信息,特别适合处理具有长期依赖关系的时间序列数据。LSTM单元的计算过程为
{f}_{t}=\sigma ({W}_{f}·[{h}_{t-1},{x}_{t}]+{b}_{f}) (15) {i}_{t}=\sigma ({W}_{i}·[{h}_{t-1},{x}_{t}]+{b}_{i}) (16) {\tilde{C}}_{t}=\mathrm{tanh}({W}_{C}·[{h}_{t-1},{x}_{t}]+{b}_{C}) (17) {C_t} = {f_t} \odot {C_{t - 1}} + {i_t} \odot {\tilde C_t} (18) {o}_{t}=\sigma ({W}_{o}·[{h}_{t-1},{x}_{t}]+{b}_{o}) (19) {h_t} = {o_t} \odot \tanh ({C_t}) (20) 式(15)~式(20)中,
{f_t} 、{i_t} 、{o_t} 分别表示遗忘门、输入门和输出门;{\tilde C_t} 、{C_t} 和{h_t} 分别表示当前时间步的候选隐藏状态、记忆单元状态和隐藏状态;{h_{t - 1}} 表示前一时间步的隐藏状态;\sigma (·) 、\mathrm{tanh}(·) 分别表示sigmoid和双曲正切激活函数;{W_f} 、{b_f} 、{W_i} 、{b_i} 、{W_C} 、{b_C} 、{W_o} 、{b_o} 为可学习参数矩阵;\odot 表示Hadamard积。本文模型采用双向LSTM结构,同时从前向和后向2个方向处理序列,并将2个方向的隐藏状态连接起来,公式为
{\vec h_t},{\vec C_t} = LST{M_{forward}}({x_t},{\vec h_{t - 1}},{\vec C_{t - 1}}) (21) {{\overset {\leftarrow} h} _t},{\overset {\leftarrow}{C} _t} = LST{M_{backward}}({x_t},{\overset {\leftarrow}{h} _{t + 1}},{\overset {\leftarrow}{C} _{t + 1}}) (22) {h_t} = [{\overset {\to} h_t},{\overset {\leftarrow}{h} _t}] (23) 式(21)~式(23)中,
{\vec h_t},{\vec C_t} 和{\overset{\leftarrow}{h} _t},{\overset{\leftarrow}{C} _t} 分别为前向和后向LSTM在时间步t 的隐藏状态和记忆单元状态;LST{M}_{forward}(·) 和LST{M}_{backward}(·) 分别为前向和后向LSTM函数;{\vec h_{t - 1}},{\vec C_{t - 1}} 和{\overset{\leftarrow}{h} _{t - 1}},{\overset{\leftarrow}{C} _{t - 1}} 分别为前向和后向LSTM在时间步t - 1 的隐藏状态和记忆单元状态;{h_t} 为双向 LSTM 在时间步t 的最终隐藏状态输出。2 实验结果与分析
本文实验数据来源于潍烟(潍坊—烟台)高铁部分路段由铁路路基沉降监测中光纤传感器探测的波长数据,选取2023年7月3日探测的波长数据作为数据集,总计
1042549 条。将该数据集的70%作为训练集、15%作为验证集、15%作为测试集。2.1 原始数据分析
2.1.1 数据概览分析
针对原始数据整体进行统计分析,分析结果为:波长数据呈现显著波动特征,波长均值为1 540.043 nm,标准差为21.347 nm,表明数据离散程度较高;分位数分析显示,25%至75%分位区间为1 530.774 nm~1 547.179 nm,跨度约16.4 nm,而极值范围则扩展至1 350.018 nm~1 749.975 nm,最大值偏离75%分位数超过200 nm,最小值低于25%分位数约180 nm,表明数据可能存在极端异常值或受突发性事件影响。
2.1.2 单点频数分布分析
以某一个探测点为例,进行单点频数分布分析,频数分布如图2所示。
通过对该探测点波长频数分布图的分析,可以观察到其波长数据呈现高度集中的尖峰分布特征。波长数据主要集中在
1 520 nm~1 570 nm的窄带范围内,其中,在约1530 nm处出现显著峰值,最高频数接近1 600 次,表明传感器在此波长区域具有较高的信号稳定性。分布整体呈现轻微的正偏斜特性,主峰右侧(约1560 nm~1 580 nm区间)存在一个频数较低但清晰可辨的次级分布区域,这种多峰结构可能反映了传感器在不同工况下的响应特性或环境因素对测量的影响。2.1.3 多点对比分析
针对同一时刻各探测点波长分布进行分析,各探测点波长分布如图3所示,在特定时刻,各探测点的波长呈现出3个明显分离的水平带状分布层次,分别位于约1 530 nm、1 543 nm和1 554 nm附近。各层内的波长值横向波动幅度较小,表明铁路路基在同一时刻各位置点的状态相对均匀。
再对全探测周期内各探测点的波长进行分析,探测周期内各探测点波长分布如图4所示。从纵向上看,每个探测点的大部分波长在时间维度上同样呈现3层分布。大多数探测点的小提琴图在中部较宽、两端渐窄,呈现典型的正态分布特征,表明波长值在各自层级的中心值附近有较高的出现频率。小提琴图延伸的垂直线条显示了各点波长在时间维度上的波动范围,可见大部分探测点的波动幅度显著大于图3中的单一时刻空间波动,这表明时间因素对波长变化的影响较为明显。
2.2 异常结果辨识
本文采用
3\sigma 原则及IQR方法对探测的波长数据进行异常结果辨识。3\sigma 方法能够较好地适应数据的整体分布特性,在保证检出真实异常的同时,有效控制误判率;而IQR方法则对分布形态不敏感,对于偏态分布或存在多峰的复杂数据结构,具有更强的适应性。通过两种方法的交叉验证,可更加可靠地识别出真正的异常值。2.2.1 单点异常结果辨识
分别利用
3\sigma 原则及IQR方法对单点波长数据进行异常结果辨识,结果分别如图5、图6所示。从单一探测点的波长数据分析可见,该点波长主要集中在1500 nm~1570 nm范围内,呈现出较为典型的单峰分布特征。应用
3\sigma 原则进行异常识别时,发现该探测点的正常波长值域为[1479.94 ,1607.62 ] nm。数据分布与拟合的正态曲线高度吻合,\mu \pm 3\sigma 区间(图5 中的绿色填充区域)覆盖了绝大多数的数据点。则将分布两侧1479.94 nm以下和1607.62 nm以上的数据被判定为异常值,这些异常数据在图5中以橙色垂直线来标注,使用3\sigma 原则检测到46个异常值,占比为2.18%,主要集中在1350 nm~1450 nm的低波长区域和1620 nm~1700 nm的高波长区域。相比之下,IQR方法在同一探测点给出的正常值域为[
1499.41 ,1586.98 ] nm,较3\sigma 原则形成的区间更为紧缩。使用IQR方法检测到76个异常值,占比3.6%。这一差异反映了两种方法的本质区别:IQR方法作为非参数统计方法,仅基于数据的排序位置确定异常阈值,不依赖数据的具体分布形式;而3\sigma 原则假设数据服从正态分布,其阈值受分布整体特性影响。2.2.2 多点异常结果辨识
铁路路基整体探测波长分布同样呈现单峰特性,但波峰更加陡峭,分布更加集中,利用
3\sigma 原则及IQR方法的结果分别如图7和图8所示。由图7可知,通过
3\sigma 原则进行异常检测得到的全局正常波长区间为[1475.47 ,1604.21 ] nm,略窄于单一探测点的区间,检测到2305 个异常值,占比2.19%。由图8可知,IQR方法进行异常检测得到的全局正常区间为[
1507.57 ,1569.17 ] nm,比单点区间进一步收窄。使用IQR方法检测到6295 个异常值,占比5.99%。这种现象说明全局数据相对更加集中,异常检测标准更加严格。这种单点与全局异常检测结果的差异表明,不同探测点的波长数据可能存在系统性差异,单独建立异常检测模型可能更为合理;同时,全局模型能够捕捉整体趋势,更易发现系统层面的异常。
2.3 预测结果与分析
2.3.1 模型训练过程
模型训练过程采用带有OneCycleLR学习率调度的AdamW优化器,在初始学习率0.001的基础上进行动态调整,确保本文模型收敛至全局最优。为提高预测精度,本文自定义了损失函数,不仅考虑预测值与真实值的均方误差,还纳入波动一致性与方向一致性约束,有效增强了本文模型对趋势变化的敏感度。通过早停机制监测验证集的损失变化过程,当连续20次训练中验证集的损失均没有进行降低时停止训练,避免过拟合。模型训练过程显示损失曲线平稳下降,如图9所示。
2.3.2 预测精度评估与误差分析
预测误差分布如图10所示,展示了本文模型在测试集上的预测偏差情况。误差直方图呈现出明显的正态分布特性,中心集中在0附近,表明模型预测总体上是无偏的。误差分布的主体范围约为±10 nm,其中,绝大多数样本的误差控制在±5 nm范围内。
本文模型在不同预测时间步上的绝对误差如图11所示。从整体趋势看,各个时间步的平均误差约保持在0~5 nm之间,表现出良好的稳定性。观察图11可知,远期预测步(如第8步~10步)的误差并未显著高于近期预测步,证明了本文设计的自注意力机制在捕捉长距离依赖关系方面的有效性。
预测波长与真实波长对比的散点图如图12所示,通过拟合发现,拟合方程与理想曲线较为相近,说明预测值与真实值间存在较高的线性相关性。
针对真实波长与预测波长时序对比分析,如图13所示,显示出预测值与真实值曲线的高度重合,变化趋势基本一致,体现了本文模型在不同预测步数下均表现出良好的预测精度。
2.3.3 性能对比
基于均方误差(MSE,Mean Squared Error)、平均绝对误差(MAE,Mean Absolute Error)及决定系数(R2)3个评价指标,将本文模型与LSTM、Bi-LSTM、Transformer、TCN和CNN-LSTM等通用模型进行对比分析,本文模型在上述指标上均表现最优,如图14~图16所示。
由图14可知,本文模型的MSE仅为18.26,远低于其他对比模型。特别是与表现最差的TCN模型相比,降低了85%以上,体现出显著的预测精度优势。
由图15可知,本文模型的MAE指标为2.69,进一步验证了的优越性,低于所有对比模型,比次优的LSTM模型还要低约26%。
由图16可知,本文模型的R2值达到0.885,显著高于其他模型,表明本文模型具有较强的拟合能力和解释能力。相比之下,传统的Transformer和TCN模型R2值仅为0.234和0.215。
综上,本文模型在预测精度、拟合优度和误差控制方面均实现了显著提升,证明了其有效性。
3 结束语
本文针对铁路路基沉降探测波长预测精度不足、适应性差的问题,构建了基于深度学习的铁路路基沉降探测波长预测模型。对波长数据进行了多维度分析,识别出波长数据呈现的3种典型分布特征。在此基础上,采用IQR方法与
3\sigma 原则相结合的异常检测机制识别异常值,为后续建模提供了高质量数据支撑。针对波长预测任务,本文设计了融合位置编码、多头自注意力、TCN与序列记忆的混合深度学习模型。该模型在测试集上的预测值与实际值相关性较好,大部分预测误差控制在±5 nm范围内,且远期预测能力不弱于近期预测,证实了该模型在长时序建模方面的优势,也验证了其在铁路路基健康监测中的应用价值,为构建预防性维护系统提供了技术支撑。下一步工作将着重于提升多源数据融合、环境因素整合及异常事件的提前预警能力,进一步增强该模型在复杂工程环境中的适应性与可靠性。
-
表 1 LKJ运行数据接口信息表
序号 内容 偏移 字节数 内容说明 1 包头 0 2 0x55 0x01 2 包号 2 1 0-FF循环 3 车次种类标识 3 4 4 车次号 7 3 5 交路号 10 1 6 车站号 11 2 7 信号机种类 13 1 8 信号机编号 14 2 9 公里标 16 3 10 线路号 19 2 工务实际线路号 11 线路标志 21 1 D6-D4:预留;D1:1-上行;D0:1-下行 12 时速 22 3 13 预留 25 6 固定填0 14 校验位 31 1 为序号2到序号13的所有字节累加和的
二进制补码合计 32 表 2 各专业检测车的检测系统、检测项目和定位标识
专业 检测系统 检测项目 定位标识 工务 轨道检测系统 轨距、轨向、高低、水平、
三角坑、轨距变化率等轨道
几何不平顺参数线路+行别+公里标 电务 信号检测系统 轨道电路、应答器、补偿电容、牵引回流等参数 线路+行别+公里标+
区间+轨道电路区段通信检测系统 GSM -R服务质量、GSM -R场强覆盖、电磁环境、电路域数据通信质量等参数 线路+行别+公里标 供电 弓网检测系统 接触线高度、拉出值、高差等接触网几何参数,以及弓网接触力、硬点等弓网动态作用
参数线路+行别+公里标+
区间+桥隧名+接触网
支柱号接触网悬挂状
态检测系统接触网悬挂松、脱、卡、磨、断等缺陷 同上 表 3 试验概况
序号 检测车 试验日期 试验线路 检测里程/km 测试时间/h 线路自动转换 1 电务试验车
WX9992932021年7月27—28日,
8月26日、10月24日宝成线、峨广线、成昆线、兴珞线 1637 45 完成2次线路自动转换,平均延迟10 s 2 接触网检测车
WX9994382024年5月11—16日 在内六线、沪昆线、黔桂线、成渝线 3878 140 完成12次线路自动转换,平均延迟8 s -
[1] 郭 瑞,陈唐龙. 基于图像处理的接触网支柱杆号识别[J]. 湖南工程学院学报,2019,29(1):18-21. [2] 朱家诚,吴 彬,吴焱明,等. 铁路接触网巡检无人车自动定位系统研究[J]. 机械设计与制造,2018(3):160-163. DOI: 10.3969/j.issn.1001-3997.2018.03.048 [3] 许 勇,邵浩东. UWB地铁轨道巡检车定位系统设计[J]. 机械设计与制造,2023(5):138-140,145. DOI: 10.3969/j.issn.1001-3997.2023.05.028 [4] 宋佳明,占 栋,陈唐龙. 接触网巡检系统空间综合定位方法[J]. 城市轨道交通研究,2023,26(9):116-121. [5] 刘玉江,杨 吉,孟景辉. 基于TAX数据的定位技术在电务检测车上的应用[J]. 铁道通信信号,2016,52(8):19-21. [6] 许海波. 铁路接触网无人检测车定位系统的研究与开发[D]. 合肥:合肥工业大学,2018. [7] 孟景辉. 绝缘节定位在铁路专业检测车中的应用探讨[J]. 铁道标准设计,2017,61(3):148-152. [8] 康 熊,王卫东,李海浪. 高速综合检测列车关键技术研究[J]. 中国铁路,2012(10):3-7. DOI: 10.3969/j.issn.1001-683X.2012.10.002 -
期刊类型引用(4)
1. 钟杰,梁琦. 全自动运行系统线路车载综合监控视频联动功能设计方案. 现代信息科技. 2024(03): 59-63 .  百度学术
百度学术
2. 刘月荣. 基于语音交互的城市轨道交通智能乘客服务系统研究. 人民公交. 2024(14): 101-103 .  百度学术
百度学术
3. 刘超. 刍议轨道交通BAS关键技术. 数字通信世界. 2023(08): 46-48 .  百度学术
百度学术
4. 赵倩,陈杨军,胡珍妮. 基于参数自适应PID控制器的轨道车辆振动控制. 电子设计工程. 2022(14): 185-189 .  百度学术
百度学术
其他类型引用(2)












 下载:
下载: