Railway network data security evaluation method based on combination weighting
-
摘要:
针对当前铁路网络安全评估中传统层次分析法（AHP，Analytic Hierarchy Process）主观性较强的问题，文章从技术防护角度出发，构建了铁路网络数据安全技术评估指标体系，并提出了一种基于AHP和熵权法的组合赋权铁路网络数据安全评估方法。通过熵权法有效挖掘指标数据的客观信息，显著削弱了主观因素对赋权结果的影响。实验结果显示，该方法能够有效降低因主观因素导致的评估误差，对铁路网络数据安全评估工作具有参考意义。
-
关键词:
- 层次分析法（AHP） /
- 熵权法 /
- 数据安全 /
- 指标 /
- 组合权重
Abstract:In response to the strong subjectivity of the traditional Analytic Hierarchy Process (AHP) in current railway network security evaluation, this paper constructed a technical evaluation index system for railway network data security from the perspective of technical protection, and proposed a combination weighting method for railway network data security evaluation based on AHP and entropy weight method. The paper effectively mined the objective information of indicator data through entropy weighting method, significantly weakened the influence of subjective factors on the weighting results. The experimental results show that this method can effectively reduce evaluation errors caused by subjective factors, and has reference significance for the evaluation of railway network data security.
-
随着智能铁路建设的不断推进，铁路网络数据规模高速增长，数据来源日趋多样[1]。海量数据的流通共享促进了数据价值的释放，但同时也对数据安全保护提出了更高要求[2]。铁路敏感数据识别和分类分级研究对落实铁路数字化转型、确保铁路网络数据安全可控具有重要意义。
目前，众多科研人员对数据敏感识别与分类分级工作开展了广泛研究。饶伟等人[3] 及宋树宝等人[4]探索了铁路数据分类分级规则制定和具体实施流程，然而人工依据规则定级存在主观性；李清欣[5]利用K-means聚类识别敏感字段，再用关联规则分析定级，但关联规则算法计算效率较低。因此，利用自然语言处理（NLP，Natural Language Processing）技术分析字段语义，并结合聚类算法确定敏感程度成为新的研究方向。彭剑峰等人[2]利用向量空间模型实现自动分类，但需要对大量字段进行人工标注；YANG等人[6]综合考虑了语义、句法和词汇信息来识别敏感数据；Gitanjali [7]提出了基于卷积的方法，利用数据中的非线性特征优化敏感数据的识别性能。然而，上述方法均难以应对真实业务场景中普遍存在的字段长度短、语义信息弱等问题。LI等人[8]提出的基于主题分析的方法突破上述限制，但由于其忽视了字段中不同敏感等级词单元的贡献差距问题，导致了对语义信息的利用产生偏差。
综上，虽然基于NLP技术的分类分级方法能凭借文本语义实现精准识别，但通常采用聚类分类结果直接作为敏感级别，定级准确性较差，且需要语料语义信息完整及大规模信息标注，缺乏实用性。因此，本文提出一种基于层次化主题分析的铁路敏感数据智能识别与分类分级方法（简称：本文方法），在语义信息和标注样本有限的情况下，实现对铁路敏感数据的准确识别与定级。
1 相关技术
本文方法利用NLP技术将字段拆分为词单元，结合分类分级知识构建主题词库；通过主题分析方法获取组成字段所有词单元的敏感级别，以计算字段分级概率向量；引入加权聚合机制缓解词单元等级分布不平衡问题，并利用层次聚类算法进行精确定级。其中，NLP技术和层次聚类算法是本文核心相关技术，距离度量方法可用于衡量数据与主题词的相似性。
1.1 NLP技术
NLP是一种通过计算机技术理解、分析和生成人类语言的技术。本文主要用到了其中的3个技术。
（1）Jieba分词：通过前缀词典将文本切分为具有意义的词汇，为文本处理提供基础。
（2）词频统计：通过构建词频表提取常见词汇，同时去除低频词，以降低模型复杂度，避免过拟合。
（3）Skip-gram模型：通过最大化中心词与上下文的条件概率来训练词向量，适用于大型语料库，可有效提升词向量质量。
1.2 聚类算法
1.2.1 K-means聚类
K-mean聚类算法基本思想是根据样本间距离将样本划分为
$ k $ 个簇，簇内样本间距离小，不同簇间样本距离大。K-means聚类算法核心步骤如下：（1） 确定
$ k $ 和最大迭代轮数，初始化簇质心；（2） 计算样本到各簇质心的距离，将样本划分到距离最小的簇中；
（3） 计算各簇内样本均值向量，并将该均值向量设为新的质心；
（4） 重复步骤（2）和（3），直至达到最大迭代轮数或质心偏移很小，输出聚类结果。
1.2.2 层次聚类算法
层次聚类[9-10]，是一种基于树状结构进行数据聚类的算法，其基本思想是通过迭代地合并或拆分簇，来创建一棵反映样本间关系的树状图。本文采用凝聚层次聚类算法，其核心步骤如下：
（1） 每个样本点作为一个单独的簇，初始化时有
$n$ 个簇；（2） 计算所有簇之间的距离矩阵；
（3） 找到距离最近的2个簇，合并为1个新的簇；
（4） 在每次合并后，更新簇之间的距离矩阵；
（5） 重复步骤（3）和（4），直至只剩下目标数量的簇为止，输出聚类结果和树状图。
实践中，存在因不同等级的敏感数据分布差异而导致类不平衡问题，此时K-means聚类等算法倾向于将数据样本判别多数类以满足其最小化目标函数的需求，从而使得最终的簇分布趋向于平衡。层次聚类算法无需预先指定簇的数量或选择质心，仅基于簇样本间的距离或相似性来构建簇，使其在处理类不平衡数据时，不会像K-means算法那样受到质心位置和簇大小的影响。因此，层次聚类算法在初始化和聚类过程中具有更好的灵活性和鲁棒性，可在一定程度上缓解数据样本类不平衡问题，从而实现对敏感数据的可靠划分。
1.3 距离度量
1.3.1 欧式距离
欧式距离计算的是2个点在多维空间中的直线距离，直观反映出数据间距，数据点
$a$ 与$b$ 间的欧式距离为$$ {S_{Euclidean}}(a,b) = \sqrt {\sum\limits_{i = 1}^n {{{({x_i} - {y_i})}^2}} } $$ (1) 式（1）中，
$ {x}_{i} $ 、$ {y}_{i} $ 分别为数据点a、b的第i维特征；n为数据点维度。1.3.2 余弦相似度
余弦距离计算的是2个向量间的夹角余弦值，反映它们在向量空间中的相似度，数据点
$a$ 与$b$ 间的余弦距离为$$ {S_{cosine}}(a,b) = 1 - \frac{{\displaystyle\sum\limits_{i = 1}^n {{x_i}} {y_i}}}{{\sqrt {\displaystyle\sum\limits_{i = 1}^n {{x_i}^2} } \sqrt {\displaystyle\sum\limits_{i = 1}^n {{y_i}^2} } }} $$ (2) 2 铁路敏感数据识别与分类分级算法
铁路敏感数据识别与分类分级算法步骤如图1所示，其中，
$ {X}^{\left\{i\right\}} $ 为铁路敏感数据X中的第i个数据点。（1）数据预处理，利用NLP技术提取数据字段语义信息，生成词空间向量；
（2）选取代表性词单元作为聚类质心，执行K-means聚类，构建主题词库；
（3）基于主题词库对字段进行主题分析，生成敏感等级初步预测结果；
（4）执行凝聚层次聚类算法实现准确定级。
2.1 数据预处理
提取每个铁路数据表的表头，将表头拆解为多个字段。采用NLP技术对铁路数据字段进行预处理，提取语义信息，构造词向量。例如，使用Jieba分词对铁路数据字段“拟接轨铁路线路名称”进行分词处理，选择合适的分词模式将字段切分成独立词单元（“拟”“接轨”“铁路”“线路”“名称”），并对分词后的结果进行词频统计，计算每个词单元在所有词单元集合中出现的频率（“拟”−47、“接轨”−
1134 、“铁路”−1245 、“线路”−1563 、“名称”−2459 ）。根据设定的过滤阈值$ {\tau _f} $ ，去除词频小于该阈值的词单元以减少噪音数据的影响，提升分类分级性能。使用Word2Vec工具训练Skip-gram模型，通过预测给定词的上下文词来学习词的向量表示，生成捕捉词之间的语义关系的词向量空间。2.2 构建主题词库
对数据进行预处理后，根据专家的经验和行业规则，为每个等级选取少量有代表性的词单元作为初始主题词
${C_0}$ ，并通过层次分析法等方法标注主题词敏感等级。其中，初始主题词总量占词典总量比例不应超过2%，且各等级主题词的比例符合字段在各等级的分布。使用${C_0}$ 作为K-means聚类的初始质心，对全部字段语料向量直接进行聚类，聚类完成后，选取每一个簇中与质心最为相近的5个字段作为强代表性语料，将其具有的与本簇质心最相近的词单元补充进主题词，最终构建主题词库$C$ 。2.3 计算数据敏感等级预测概率向量
在词单元层面进行主题分析，再结合定级策略计算数据字段敏感等级预测概率向量。具体来说，先计算与每个词单元相似度最高的主题，按照不同等级主题出现的频率，生成该字段的初步敏感等级预测概率向量。例如，字段由5个词单元构成，其中有2个1级词、2个2级词、1个3级词，则初步预测概率为（0.4，0.4，0.2）。考虑到铁路数据敏感级别分布不平衡，结合定级策略对分级概率向量进行加权聚合并归一化处理，初步确定字段敏感等级。例如，制定加权策略，3级加权10倍、2级加权2倍、1级不加权，修正后的预测概率向量为（0.125， 0.25，0.625），则该字段初步定级为3级词。
2.4 通过层次聚类判定数据敏感等级
若字段对2个及以上等级预测概率之差≤
${\tau _d}$ ，即当预测概率向量无法以高置信度确定字段敏感等级时，利用层次聚类算法进一步判定数据敏感等级，否则将字段初步定级结果作为最终输出。具体方法为，对该字段语料向量和$C$ 进行凝聚层次聚类，使用合适的距离度量方式衡量字段向量与主题词的相似性，逐步合并最相似的簇，直到当前划分簇的数量等于敏感等级数量L。对于字段所在簇，统计簇中含有的2个或多个等级的主题词占比（只考虑概率接近的等级），输出占比高对应的等级作为字段的最终敏感等级。2.5 本文方法特点
本文方法和常规方案区别主要有以下方面。
（1）在语义信息利用方面，常规方案通常使用组成字段词单元向量的均值作为字段向量，但字段中不同词单元对字段敏感等级的贡献不同，仅使用均值向量会导致词单元信息难以被利用。本文基于主题分析判定词单元级别敏感程度，再计算字段敏感级别，实现语义信息的充分利用。
（2）在定级算法设计方面，常规方案直接对主题词进行K-means聚类，将字段向量距离最近的簇质心敏感级别作为字段敏感级别，因此字段定级主要依赖于最终轮得到的
$L$ 个质心（主题词），定级方式较为主观。本文采用主题分析初步确定字段敏感等级预测向量，对于区分度较低的字段再使用层次聚类算法判定最终敏感等级，具有较强的可解释性。（3）在处理字段敏感等级不平衡的问题方面，本文在构建主题词库阶段，根据字段敏感等级比例选取主题词，以避免分级方法对特定敏感等级主题的过度偏好或忽视；结合定级策略修正分级概率向量，旨在提升少数敏感等级字段定级的准确性；采用凝聚层次聚类算法进一步确定敏感等级，不会像K-means算法那样受到质心位置和簇大小的影响，具有更好的灵活性和鲁棒性。
3 实验与分析
为评估基于层次化主题分析的敏感数据识别与分类分级方法的效果，本文收集铁路敏感字段数据作为实验数据集，通过比较本文方法在不同权重、不同词频阈值下的总体准确率、各敏感等级准确率等指标上的表现，选定最优超参数。最终，将本文方法与基于语义分析和K-means聚类的传统主题分析法（简称：基线方法）进行对比与分析。
3.1 数据集构建
本文收集铁路敏感数据并采用NLP技术对其进行预处理，根据铁路数据分类分级要求，按照数据的重要程度将数据划分为一般数据、重要数据和核心数据，数据等级由低到高表示为1～3级，其中一般数据细化分级为S1～S4。由于细化一般数据分类分级流程与前述算法一致，因此在实验环节，以划分1～3级为例，构造铁路敏感数据集并标注各等级对应的数据量，如表1所示。
表 1 铁路敏感数据集各等级数据量数据名称 核心数据 重要数据 一般数据 数据等级 3 2 1 数据量/条 83 4848 40313 3.2 评估指标
3.2.1 敏感等级识别准确率
敏感等级识别准确率的公式为
$$ Accuracy = \frac{{{N_c}}}{{{N_{all}}}} $$ (3) 式（3）中，
$ {N_{all}} $ 为待分级数据的总数量；$ {N_c} $ 为正确分级的数据数量。3.2.2 混淆矩阵
混淆矩阵中的任意值
$C{M_{i,j}}$ 的定义为，真实标签属于第$i$ 类，且预测标签属于第$j$ 类的文本数量。混淆矩阵展示了模型预测结果与实际标签之间的关系，可帮助理解模型在哪些类别上表现良好，以及在哪些类别上可能存在问题。3.2.3 类召回率
对于某一个敏感等级
$i$ ，其类召回率的公式为$$ Recal{l_i} = \frac{{T{P_i}}}{{T{P_i} + F{N_i}}} $$ (4) 式（4）中，
$T{P_i}$ 表示真实敏感等级$i$ 中正确分级的数据的数量；$F{N_i}$ 表示真实敏感等级$i$ 中错误分级的数据的数量。类召回率主要关注于该类正确样本的检测能力，在不平衡数据集中，召回率（特别是对于少数类）可作为一个更有意义的指标。3.3 参数调试
本文方法需要预先指定词频过滤阈值
${\tau _f}$ 和加权系数，并选定适合的距离度量函数。本文针对不同的参数设置进行实验，分析实验结果并找出最优的参数配置。3.3.1 词频过滤阈值
在使用NLP技术对铁路敏感数据进行预处理时，需要指定删去低频词的过滤阈值，不同的阈值设定会对方法的性能产生较大的影响。因此，本小节在词频过滤阈值为25、50、75、100和150时，分别对主题分析[8]、使用余弦距离的层次化主题分析、使用欧式距离的层次化主题分析这3个方法进行了敏感等级识别准确率的评估，实验结果如图2所示。
由实验结果可看出，3个方法的敏感等级识别准确率都在词频过滤阈值等于50时达到最高。因此，将词频过滤阈值设置为50，可达到相对最佳的识别效果。
3.3.2 距离度量函数
在机器学习算法中，距离度量函数的选取至关重要，不同的距离度量函数会对算法的性能产生显著的影响。本文分别使用余弦距离和欧式距离结合本文方法进行实验，实验结果如图2所示。由实验结果可看出，在选取任何词频过滤值的情况下，采用欧式距离方法的性能均优于采用余弦距离方法的性能。因此，选用欧式距离作为本文方法的距离度量函数更为合适。
3.3.3 加权系数
由于在字段中不同敏感等级的词单元对字段的敏感等级贡献不同，并且铁路数据敏感级别分布也较不均衡，因此，需要对归属于不同敏感等级的词单元对概率值的贡献进行加权。加权系数的选择是影响算法性能的关键因素。本文选取5组不同的加权系数（一般数据∶重要数据∶核心数据）进行实验，实验结果如表2所示。
表 2 不同加权系数的准确率与类召回率加权系数 敏感等级识别
准确率一般数据
召回率重要数据
召回率核心数据
召回率1:1:10 86.74% 94.21% 25.27% 77.14% 1:1.5:10 83.64% 89.56% 34.73% 77.14% 1:2:10 83.35% 89.21% 35.12% 77.14% 1:2.5:10 81.67% 86.43% 41.87% 77.14% 1:3:10 80.18% 84.58% 44.13% 77.14% 从表2可以看出，当重要数据的加权比例增大时，本文方法对重要数据的召回率会显著提高，但会牺牲部分一般数据的召回率，且使全部数据的敏感等级识别准确率降低。因此，本文方法可根据不同的定级策略，调整加权系数，权衡模型对不同敏感等级数据的倾向性。
由于在加权系数为1:1:10时，敏感等级识别准确率显著高于其他几组实验，因此，本文后续实验将在此配置下进行。
3.4 实验结果分析
根据3.3中给出的实验配置，测试本文方法和基线方法，实验产生的混淆矩阵如图3所示。
根据实验结果，计算出敏感等级识别准确率和各等级的类召回率，如表3所示。
表 3 本文方法与基线方法的准确率与类召回率敏感等级识别
准确率一般数据
召回率重要数据
召回率核心数据召回率 本文方法 86.74% 94.21% 25.27% 77.14% 基线方法 83.79% 89.21% 39.01% 67.47% 层次化主题分析的敏感等级识别准确率、一般数据召回率、核心数据召回率均优于基线方法，而重要数据召回率上的不足可根据3.3.3小节中对定级策略的倾向性不同，修改加权系数，弥补方法在重要数据识别上的缺陷。
综上，本文方法显著优于基线方法，并且提供了加权系数，引入了针对不同定级策略的算法可调节性，可灵活应用于不平衡的敏感数据。
4 结束语
本文提出一种基于层次化主题分析的敏感数据识别与分类分级方法，通过主题分析实现词单元敏感度定级，计算字段敏感分级概率并利用层次聚类算法进行修正。实验结果表明，本文提出的方法能有效缓解敏感等级分布不平衡对字段定级的影响，且支持定级策略的动态调整。受益于层次化主题分析的灵活性，本文提出的方法能够直接迁移到铁路重要系统数据分类分级现有技术方案内，对现有技术进行补强。此外，分类分级的输出可用于和铁路实际系统中信息表定级结果作对比，帮助分析和检查既有记录的敏感等级定级是否合理。由于层次聚类算法在计算复杂度和内存消耗方面存在局限性，下一步将考虑优化聚类阶段的效率，以提升大规模字段敏感识别和分类分级的处理时间。
-
表 1 铁路网络数据安全技术评估标准
评估等级 分值 详细说明 低风险 S$\geqslant$80 被评估数据安全技术防护处于较高安全状态，
风险较低中风险 80＞S＞60 被评估数据安全技术防护存在一定安全隐患，
但风险可控高风险 S$\leqslant $60 被评估数据安全技术防护存在较大安全隐患，
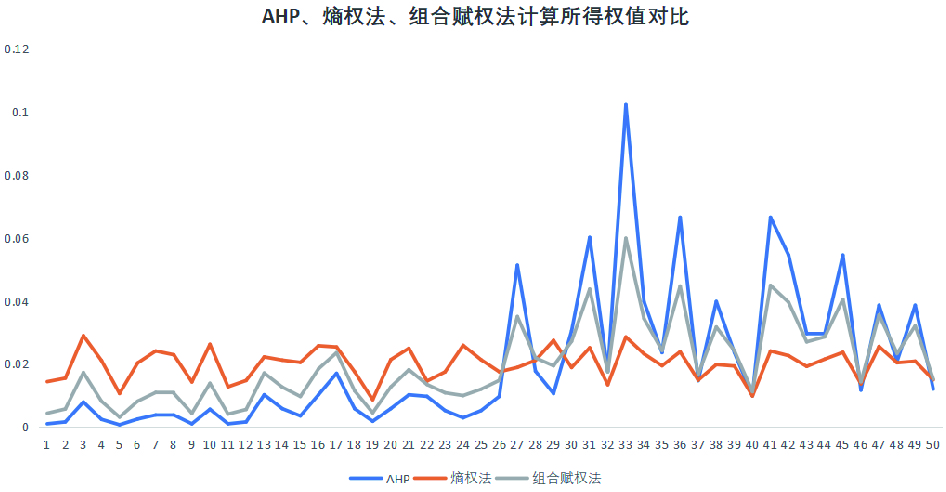
应立即修复，降低风险
下载: 导出CSV
表 2 AHP、熵权法和组合赋权法计算权重值的对比
指标 $ {w}_{1} $ $ {w}_{2} $ $ {w}_{3} $ $ {w}_{4} $ $ {w}_{5} $ $ {w}_{6} $ $ {w}_{7} $ $ {w}_{8} $ $ {w}_{9} $ $ {w}_{10} $ AHP $ 0.001\ 0 $ $0.001\;6 $ $0.007\;9 $ $0.002\;4 $ $0.000\;7 $ $0.002\;5 $ $0.003\;8 $ $0.003\;8 $ $0.001 $ $0.005\;6 $ 熵权法 $ 0.014\;4 $ $ 0.015\;5 $ $ 0.029\;0 $ $ 0.021\;1 $ $ 0.010\;6 $ $ 0.020\;3 $ $ 0.024\;1 $ $ 0.022\;9 $ $ 0.014\;3 $ $ 0.026\;2 $ 组合赋权 $ 0.004\;3 $ $ 0.005\;7 $ $ 0.017\;3 $ $ 0.008\;1 $ $ 0.003\;1 $ $ 0.008\;2 $ $ 0.010\;9 $ $ 0.010\;7 $ $ 0.004\;3 $ $ 0.013\;8 $ 指标 $ {w}_{11} $ $ {w}_{12} $ $ {w}_{13} $ $ {w}_{14} $ $ {w}_{15} $ $ {w}_{16} $ $ {w}_{17} $ $ {w}_{18} $ $ {w}_{19} $ $ {w}_{20} $ AHP $ 0.001\ 0 $ $ 0.001\;6 $ $ 0.010\;2 $ $ 0.005\;8 $ $ 0.003\;5 $ $ 0.010\;2 $ $ 0.017\ 0 $ $ 0.005\;8 $ $ 0.001\;8 $ $ 0.005\;8 $ 熵权法 $ 0.012\;7 $ $ 0.014\;7 $ $ 0.022\;2 $ $ 0.021\;2 $ $ 0.020\;5 $ $ 0.025\;8 $ $ 0.025\;4 $ $ 0.017\;5 $ $ 0.008\;6 $ $ 0.021\;3 $ 组合赋权 $ 0.004\;1 $ $ 0.005\;5 $ $ 0.017\;1 $ $ 0.012\;6 $ $ 0.009\;7 $ $ 0.018\;4 $ $ 0.023\;6 $ $ 0.011\;5 $ $ 0.004\;5 $ $ 0.012\;7 $ 指标 $ {w}_{21} $ $ {w}_{22} $ $ {w}_{23} $ $ {w}_{24} $ $ {w}_{25} $ $ {w}_{26} $ $ {w}_{27} $ $ {w}_{28} $ $ {w}_{29} $ $ {w}_{30} $ AHP $ 0.010\;2 $ $ 0.009\;7 $ $ 0.005\;2 $ $ 0.002\;9 $ $ 0.005\;2 $ $ 0.009\;7 $ $ 0.051\;3 $ $ 0.017\;7 $ $ 0.010\;6 $ $ 0.030\;5 $ 熵权法 $ 0.025\;0 $ $ 0.014\;5 $ $ 0.017\;5 $ $ 0.025\;9 $ $ 0.021\;3 $ $ 0.017\;5 $ $ 0.018\;9 $ $ 0.021\;1 $ $ 0.027\;5 $ $ 0.018\;9 $ 组合赋权 $ 0.018\;1 $ $ 0.013\;5 $ $ 0.010\;8 $ $ 0.010\;0 $ $ 0.012\;0 $ $ 0.014\;8 $ $ 0.035\;0 $ $ 0.021\;9 $ $ 0.019\;4 $ $ 0.027\;1 $ 指标 $ {w}_{31} $ $ {w}_{32} $ $ {w}_{33} $ $ {w}_{34} $ $ {w}_{35} $ $ {w}_{36} $ $ {w}_{37} $ $ {w}_{38} $ $ {w}_{39} $ $ {w}_{40} $ AHP $ 0.060\;1 $ $ 0.017\;7 $ $ 0.102\;2 $ $ 0.039\;8 $ $ 0.023\;6 $ $ 0.066\;5 $ $ 0.014\;7 $ $ 0.039\;8 $ $ 0.023\;6 $ $ 0.009\;9 $ 熵权法 $ 0.025\;1 $ $ 0.013\;4 $ $ 0.028\;5 $ $ 0.023\;2 $ $ 0.019\;4 $ $ 0.023\;9 $ $ 0.014\;9 $ $ 0.019\;8 $ $ 0.019\;3 $ $ 0.009\;8 $ 组合赋权 $ 0.043\;7 $ $ 0.017\;4 $ $ 0.059\;8 $ $ 0.034\;4 $ $ 0.024\;3 $ $ 0.044\;7 $ $ 0.016\;7 $ $ 0.031\;7 $ $ 0.024\;2 $ $ 0.011\;2 $ 指标 $ {w}_{41} $ $ {w}_{42} $ $ {w}_{43} $ $ {w}_{44} $ $ {w}_{45} $ $ {w}_{46} $ $ {w}_{47} $ $ {w}_{48} $ $ {w}_{49} $ $ {w}_{50} $ AHP $ 0.066\;5 $ $ 0.054\;5 $ $ 0.029\;6 $ $ 0.029\;6 $ $ 0.054\;5 $ $ 0.011\;7 $ $ 0.038\;6 $ $ 0.020\;8 $ $ 0.038\;6 $ $ 0.012\ 0 $ 熵权法 $ 0.024\;1 $ $ 0.022\;6 $ $ 0.019\;2 $ $ 0.021\;5 $ $ 0.023\;7 $ $ 0.013\;7 $ $ 0.025\;5 $ $ 0.020\;4 $ $ 0.020\;9 $ $ 0.015\;0 $ 组合赋权 $ 0.044\;9 $ $ 0.039\;5 $ $ 0.027\;0 $ $ 0.028\;6 $ $ 0.040\;5 $ $ 0.014\;3 $ $ 0.035\;5 $ $ 0.023\;3 $ $ 0.032\;1 $ $ 0.015\;2 $
下载: 导出CSV
-
[1] 铁道技术监督编辑部. 新时代交通强国铁路先行规划纲要[J]. 铁道技术监督,2020,48(9):1-6,24. DOI: 10.3969/j.issn.1006-9178.2020.09.001 [2] 孙永福,吴 昊,林晓言,等. 铁路建设项目综合评价指标体系与方法[J]. 铁道学报,2023,45(9):1-11. DOI: 10.3969/j.issn.1001-8360.2023.09.001 [3] 刘国梁,姚洪磊,解辰辉,等. 基于层次分析法的铁路网络安全检查评价方法研究[J]. 铁路计算机应用,2023,32(11):6-10. DOI: 10.3969/j.issn.1005-8451.2023.11.02 [4] 郑晓波. 基于AHP的铁路信息系统风险评价指标体系[J]. 中国安全科学学报,2020,30(S1):139-145. DOI: 10.16265/j.cnki.issn1003-3033.2020.S1.025. [5] 陈 路. 熵权法在信息安全风险评估中的应用[J]. 信息系统工程,2021,34(9):62-64. [6] 顾兆军,李怀民,丁 磊,等. 基于组合权重的工控系统安全形式化分析方法[J]. 计算机仿真,2022,39(12):422-428. DOI: 10.3969/j.issn.1006-9348.2022.12.078 [7] 刘彦麟,李 琪,吕晓艳,等. 基于层次分析法的铁路旅客换乘方案选择权重研究[J]. 铁路计算机应用,2019,28(11):9-12. DOI: 10.3969/j.issn.1005-8451.2019.11.003 [8] 邱菀华. 管理决策与应用熵学[M]. 北京:机械工业出版社,2002. -
期刊类型引用(3)
1. 张思楠，李树彬，曹永军. 基于LSTM-Transformer的城市轨道交通短时客流预测. 物流科技. 2024(14): 103-106+114 . 
百度学术
2. 张瑞，席一丹，白惠君，周晓渊，韩峰宇. 基于WT-SLSTM模型的交通流预测研究. 山西交通科技. 2023(04): 129-133 . 百度学术
3. 周明杉，卫铮铮，李聚宝. 基于突发公共卫生事件影响下的铁路客流量恢复率预测研究. 铁道运输与经济. 2023(12): 57-64 . 百度学术
其他类型引用(4)
计量
- 文章访问数: 99
- HTML全文浏览量: 28
- PDF下载量: 30
- 被引次数: 7
