Railway network data security evaluation method based on combination weighting
-
摘要:
针对当前铁路网络安全评估中传统层次分析法（AHP，Analytic Hierarchy Process）主观性较强的问题，文章从技术防护角度出发，构建了铁路网络数据安全技术评估指标体系，并提出了一种基于AHP和熵权法的组合赋权铁路网络数据安全评估方法。通过熵权法有效挖掘指标数据的客观信息，显著削弱了主观因素对赋权结果的影响。实验结果显示，该方法能够有效降低因主观因素导致的评估误差，对铁路网络数据安全评估工作具有参考意义。
-
关键词:
- 层次分析法（AHP） /
- 熵权法 /
- 数据安全 /
- 指标 /
- 组合权重
Abstract:In response to the strong subjectivity of the traditional Analytic Hierarchy Process (AHP) in current railway network security evaluation, this paper constructed a technical evaluation index system for railway network data security from the perspective of technical protection, and proposed a combination weighting method for railway network data security evaluation based on AHP and entropy weight method. The paper effectively mined the objective information of indicator data through entropy weighting method, significantly weakened the influence of subjective factors on the weighting results. The experimental results show that this method can effectively reduce evaluation errors caused by subjective factors, and has reference significance for the evaluation of railway network data security.
-
随着铁路技术不断创新发展，铁路基础设施水平也在不断提升，其中，供电设备尤其是接触网设备的质量在铁路运营中至关重要，其性能直接影响到列车的运行速度和稳定性。为了提升接触网设备安装和维护的质量，在安装完成后和运营维护（简称：运维）过程中，均需要进行几何参数检测。
接触网几何参数检测主要分为人工与机械测量、接触式与非接触式测量、便携式与车载测量等类型。我国主要采用2种检测方式：（1）在受电弓上安装传感器的接触式测量，使用综合检测车和接触网动检车，其优势在于动态测量、高效率和强大的数据分析能力[1]；（2）非接触式测量，主要利用激光技术，如激光测量仪和测量小车，在新线接触网精调、问题复测定位及检修确认等环节中发挥重要作用[2]。李育冰等人[3]为了提高接触网激光检测仪自动化水平，在分析现有接触网激光仪的基本情况基础上，提出了运用图像处理加自动扫描技术实现接触网激光检测仪自动测量的方法；陈忠斌等人[4]针对电气化铁路检修工区接触网日常巡检的需求，研制了一种便携式激光测量仪，用于接触网几何参数的日常检测；豆孝磊[5]研究基于车载激光扫描的接触网几何参数自动检测，以便更高效地满足日常养护维修的需要。
传统的激光测量仪在线路新建和运营过程中，均发挥着重要作用，但目前仍主要利用人工录入或导出表格的方式记录激光测量仪的检测数据，检测过程消耗人力大、工作效率低，且缺乏自动统计、分析的手段。因此，本文基于激光测量、蓝牙传输、数据分析等技术，设计接触网几何参数检测系统（简称：检测系统），实现对接触网几何参数数据的自动采集、传输、存储和分析，在保障检测质量前提下同时减少人力消耗，提高检测效率[6-7]。
1 系统设计
1.1 业务流程
接触网几何参数检测业务流程如图1所示。
检测系统融合激光测量、蓝牙、数据分析等技术，基于可移动激光测量仪器完成接触网各项几何参数测量，采用蓝牙技术完成数据传输汇总，结合数据分析技术，完成几何参数数据统计分析与缺陷分析，并通过数据共享接口，集成铁路工程管理平台关于铁路项目基础、工程实体分解等方面的业务数据，实现对铁路接触网几何参数采集到分析预警全业务流程的质量控制[8]。
1.2 总体架构
以铁路工程接触网几何参数检测业务需求为导向，采用基于B/S的架构体系，以面向铁路工程接触网自动化采集分析为目标，从数据采集、数据传输、数据存储、数据分析等方面构建检测系统。该系统依托中国铁路主数据中心，对网络、存储、计算等资源进行统一分配管理，为其平稳运行提供统一的底层支撑环境，符合信息规范标准体系，满足安全、运维保障体系要求。检测系统总体架构如图2所示。
1.2.1 运行环境
以中国铁路主数据中心为支撑，配置存储、计算、网络、安全等数据资源，保障系统高性能、高可靠运行。
1.2.2 数据层
数据层通过关系型MySQL数据库，将铁路工程基础数据、接触网几何参数业务数据等进行统一存储，在系统运行过程中，利用 Redis 键值对数据库存储缓存数据，以此加快数据读取速度。
1.2.3 管理层
管理层主要将通用数据与几何参数数据进行统一管理。检测系统从铁路工程建设系统基础数据服务中获取基础数据、用户数据及角色数据。
1.2.4 业务层
业务层包含了支撑接触网几何参数检测业务的功能主体，包括数据接收、参数曲线汇总、进度分析、统计分析、缺陷分析及质量评级等。
1.2.5 展示层
支持各级用户通过PC浏览器、智能移动终端等不同方式访问检测系统。
1.3 技术架构
检测系统同时对硬件和软件进行了集成，支持持续集成（CI，Continuous Integration）和持续交付（CD，Continuous Delivery），其技术架构如图3所示。
1.3.1 设施层
设施层是检测系统的基础，运用云计算、云存储技术提高系统的高可用性和扩展性，利用负载均衡、网络安全与监控运维技术提高系统的稳定性，维持系统高性能运行。
1.3.2 存储层
存储层是检测系统的数据中心，系统数据种类多、数据量大，利用高性能内存数据库Redis承载缓存服务，提高数据访问速度；利用MySQL对结构化数据进行存储，满足平台高并发需求；利用对象存储对模型文件进行统一管理。
1.3.3 平台层
平台层是检测系统的中枢大脑，分为底层开发框架、系统服务和认证服务这3部分。
（1）底层开发框架：利用SpringBoot框架和VUE框架支撑平台前后端开发；利用认证授权技术限制平台访问，降低数据泄漏可能；利用日志框架实现问题的快速定位，支撑系统问题的快速修复；
（2）系统服务：用于处理相关功能业务。其中，数据接收服务用于接收上传的几何参数；缺陷分析服务用于统计分析几何参数。
（3）认证服务：保障检测系统安全并限制用户访问权限，主要技术包括API访问认证技术、身份认证技术及权限认证技术等。
1.3.4 服务网关
服务网关作为单一访问点，充当多项服务的代理，支持 Biz GateWay、App GateWay、Admin GateWay、File GateWay 等网关类型。它能够启用跨所有服务的变换、路由和公共处理，为各类服务的访问与交互提供统一的入口与管理机制。
1.3.5 访问控制
用于对系统访问进行限制或提高访问量。使用内容分发网络（CDN）加速技术、Linux虚拟服务器（LVS）负载技术及Nginx静态资源技术提高网络访问速度。
1.3.6 展示层
展示层分为移动端和Web端，移动端采用Android原生技术或H5技术进行研发；Web端使用VUE+ElmentUI技术进行研发。
2 系统功能
检测系统分为移动端和Web端。移动端包含登录、基数数据下载、蓝牙连接测量仪器、接收仪器传输数据、展示待上传数据、查询接触网几何参测量历史数据、对缺陷数据标注等功能；Web端包含测量仪器初始化、缺陷阈值范围设置、工程结构树展示、接收移动端测量数据、测量数据展示、缺陷数据标注、参数曲线绘制、测量进度数据统计、缺陷数据统计、区间质量评级等功能。
2.1 数据快速采集
激光测量仪器集成了采用激光测距、光栅测角技术的二维坐标测量系统和传感信息融合技术，实现对绝大部分接触网几何参数项的测量。
（1）激光测量仪器主机部分功能包括接触网几何参数测量、数据存储、数据传输（U盘、RS232、蓝牙），支持白天和黑夜测量模式，同时通过轨道上的滑轮移动实现了可移动测量。
（2）激光测量仪器支持对接触网的导高、拉出值、线岔中心、500 mm处高差、轨距、超高（水平）、红线、侧面限界、承力索与接触线高差、跨铁道输电线与接触线的距离、锚段关节、定位器皮度、自由测量、跨距测量等14项几何参数的测量。
（3）激光测量仪器测量出结果值后，通过蓝牙将数据发送至移动端，移动端选择接收或不接收，测量完成后可快速移动至下一个测点。
2.2 数据传输
移动端通过选择附近开启的蓝牙与测量仪器进行连接，接收测量仪器发送的测量数据，将数据进行缓存，同时支持在隧道内无网络信号时接收数据，待到网络信号良好时，一键上传测量数据至服务端。在Web端界面上通过不同颜色表达出数据超限预警，满足数据即测即传即预警需求。
移动端支持数据接收和数据上传功能，同时支持查看整个线路的测量数据，管理层和负责人通过手机查看测量数据的质量和测量进度，为管理和决策提供了数据支撑，保障接触网工程建设进度有序推进。
2.3 接触网几何参数数据统计分析
使用数据统计分析技术，对接触网几何参数测量数据进行统计分析，从标段、工点、锚段维度和关键几何参数项维度统计分析支柱总数、已测量支柱数量及缺陷数量。统计分析界面如图4所示。
2.4 阈值设置与缺陷展示
设置标准值、状态值、警示值、限界值的阈值范围，并支持对单项支柱阈值范围进行修改。测量数据标记为红色或橘黄色表示有缺陷，如图5所示。
2.5 质量评级
检测系统基于测量数据客观真实地判识缺陷，通过对缺陷类型和数量的统计，形成对锚段、站区、作业队的质量评级，提升接触网工程施工质量。
（1）锚段的质量评级：根据锚段内发现的缺陷等级和数量来评定，锚段的质量评级分为3个级别：优、良、差，如果缺陷等级较高且数量较多，则锚段的质量评级较低。
（2）站区/作业队的质量评级：依据站区/作业队内优良锚段的比例来评定，即优良锚段的数量与站区/作业队内锚段总数的比例。如果优良锚段的比例高，则站区/作业队的整体质量评级较好。
3 关键技术
3.1 激光测量仪器改造及测量数据无线传输技术
由于激光测量仪器无法直接连接数据接收服务器，通过添加蓝牙硬件模块改造测量仪器，支持激光测量仪器与移动端通过蓝牙模块进行连接，建立数据传输通道，便于几何参数测量数据快速传输和便捷处理。将采集数据传输到移动端后，再通过互联网技术传输到数据接收服务器。
3.2 缺陷自动识别与预警技术
在各项接触网几何参数的缺陷阈值范围下，根据设置的标准值、状态值、警示值、限界值阈值范围对几何参数测量值进行自动判识，利用不同颜色对缺陷进行等级标注，使施工测量人员通过查看数据列表快速了解缺陷发生的位置，尽早采取调整措施。
4 应用效果
检测系统已在西延（西安—延安）、贵南（贵阳—南宁）等多个铁路项目中进行了广泛应用，依托检测系统开展接触网施工安装调试后几何参数的测量工作，构建了基于可移动激光测量仪的接触网几何参数自动采集分析全过程检测模式。在提高测量精度的同时，提升了检测效率。
在接触网精调时，通过边测试边调整减少返工工作；通过检测系统即测即传即预警，实现接触网检测数据动态采集与分析；对锚段进行优良评级，对站区和作业队进行优良占比统计，通过评级考核，提高了接触网工程施工质量。
5 结束语
本文设计接触网几何参数检测系统，通过集成蓝牙技术和数据传输技术，使用移动端作为数据传输的中介，有效解决了测量仪器与数据服务端之间的数据自动传输问题。该系统不仅实现了接触网几何参数的高效测量和数据存储，还通过智能分析快速识别数据质量缺陷，极大增强了检测人员和管理人员在接触网几何参数检测工作中的效率。
-
表 1 铁路网络数据安全技术评估标准
评估等级 分值 详细说明 低风险 S$\geqslant$80 被评估数据安全技术防护处于较高安全状态，
风险较低中风险 80＞S＞60 被评估数据安全技术防护存在一定安全隐患，
但风险可控高风险 S$\leqslant $60 被评估数据安全技术防护存在较大安全隐患，
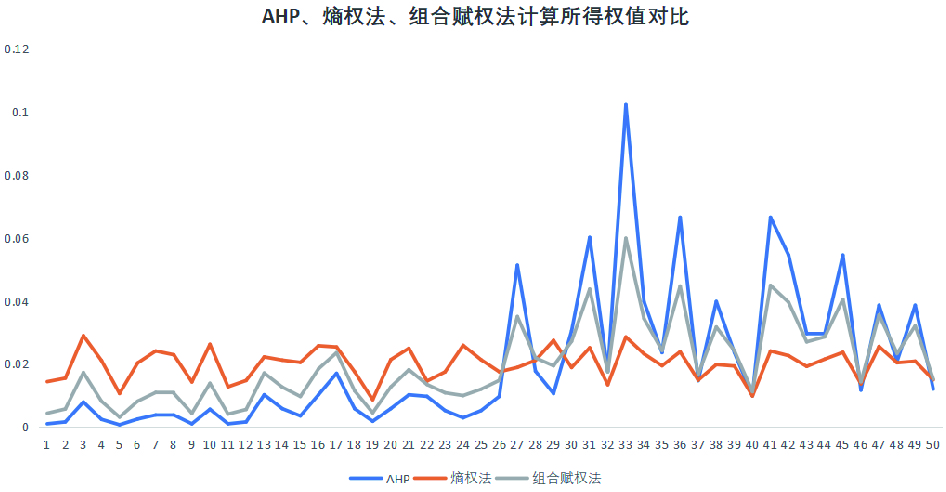
应立即修复，降低风险
下载: 导出CSV
表 2 AHP、熵权法和组合赋权法计算权重值的对比
指标 $ {w}_{1} $ $ {w}_{2} $ $ {w}_{3} $ $ {w}_{4} $ $ {w}_{5} $ $ {w}_{6} $ $ {w}_{7} $ $ {w}_{8} $ $ {w}_{9} $ $ {w}_{10} $ AHP $ 0.001\ 0 $ $0.001\;6 $ $0.007\;9 $ $0.002\;4 $ $0.000\;7 $ $0.002\;5 $ $0.003\;8 $ $0.003\;8 $ $0.001 $ $0.005\;6 $ 熵权法 $ 0.014\;4 $ $ 0.015\;5 $ $ 0.029\;0 $ $ 0.021\;1 $ $ 0.010\;6 $ $ 0.020\;3 $ $ 0.024\;1 $ $ 0.022\;9 $ $ 0.014\;3 $ $ 0.026\;2 $ 组合赋权 $ 0.004\;3 $ $ 0.005\;7 $ $ 0.017\;3 $ $ 0.008\;1 $ $ 0.003\;1 $ $ 0.008\;2 $ $ 0.010\;9 $ $ 0.010\;7 $ $ 0.004\;3 $ $ 0.013\;8 $ 指标 $ {w}_{11} $ $ {w}_{12} $ $ {w}_{13} $ $ {w}_{14} $ $ {w}_{15} $ $ {w}_{16} $ $ {w}_{17} $ $ {w}_{18} $ $ {w}_{19} $ $ {w}_{20} $ AHP $ 0.001\ 0 $ $ 0.001\;6 $ $ 0.010\;2 $ $ 0.005\;8 $ $ 0.003\;5 $ $ 0.010\;2 $ $ 0.017\ 0 $ $ 0.005\;8 $ $ 0.001\;8 $ $ 0.005\;8 $ 熵权法 $ 0.012\;7 $ $ 0.014\;7 $ $ 0.022\;2 $ $ 0.021\;2 $ $ 0.020\;5 $ $ 0.025\;8 $ $ 0.025\;4 $ $ 0.017\;5 $ $ 0.008\;6 $ $ 0.021\;3 $ 组合赋权 $ 0.004\;1 $ $ 0.005\;5 $ $ 0.017\;1 $ $ 0.012\;6 $ $ 0.009\;7 $ $ 0.018\;4 $ $ 0.023\;6 $ $ 0.011\;5 $ $ 0.004\;5 $ $ 0.012\;7 $ 指标 $ {w}_{21} $ $ {w}_{22} $ $ {w}_{23} $ $ {w}_{24} $ $ {w}_{25} $ $ {w}_{26} $ $ {w}_{27} $ $ {w}_{28} $ $ {w}_{29} $ $ {w}_{30} $ AHP $ 0.010\;2 $ $ 0.009\;7 $ $ 0.005\;2 $ $ 0.002\;9 $ $ 0.005\;2 $ $ 0.009\;7 $ $ 0.051\;3 $ $ 0.017\;7 $ $ 0.010\;6 $ $ 0.030\;5 $ 熵权法 $ 0.025\;0 $ $ 0.014\;5 $ $ 0.017\;5 $ $ 0.025\;9 $ $ 0.021\;3 $ $ 0.017\;5 $ $ 0.018\;9 $ $ 0.021\;1 $ $ 0.027\;5 $ $ 0.018\;9 $ 组合赋权 $ 0.018\;1 $ $ 0.013\;5 $ $ 0.010\;8 $ $ 0.010\;0 $ $ 0.012\;0 $ $ 0.014\;8 $ $ 0.035\;0 $ $ 0.021\;9 $ $ 0.019\;4 $ $ 0.027\;1 $ 指标 $ {w}_{31} $ $ {w}_{32} $ $ {w}_{33} $ $ {w}_{34} $ $ {w}_{35} $ $ {w}_{36} $ $ {w}_{37} $ $ {w}_{38} $ $ {w}_{39} $ $ {w}_{40} $ AHP $ 0.060\;1 $ $ 0.017\;7 $ $ 0.102\;2 $ $ 0.039\;8 $ $ 0.023\;6 $ $ 0.066\;5 $ $ 0.014\;7 $ $ 0.039\;8 $ $ 0.023\;6 $ $ 0.009\;9 $ 熵权法 $ 0.025\;1 $ $ 0.013\;4 $ $ 0.028\;5 $ $ 0.023\;2 $ $ 0.019\;4 $ $ 0.023\;9 $ $ 0.014\;9 $ $ 0.019\;8 $ $ 0.019\;3 $ $ 0.009\;8 $ 组合赋权 $ 0.043\;7 $ $ 0.017\;4 $ $ 0.059\;8 $ $ 0.034\;4 $ $ 0.024\;3 $ $ 0.044\;7 $ $ 0.016\;7 $ $ 0.031\;7 $ $ 0.024\;2 $ $ 0.011\;2 $ 指标 $ {w}_{41} $ $ {w}_{42} $ $ {w}_{43} $ $ {w}_{44} $ $ {w}_{45} $ $ {w}_{46} $ $ {w}_{47} $ $ {w}_{48} $ $ {w}_{49} $ $ {w}_{50} $ AHP $ 0.066\;5 $ $ 0.054\;5 $ $ 0.029\;6 $ $ 0.029\;6 $ $ 0.054\;5 $ $ 0.011\;7 $ $ 0.038\;6 $ $ 0.020\;8 $ $ 0.038\;6 $ $ 0.012\ 0 $ 熵权法 $ 0.024\;1 $ $ 0.022\;6 $ $ 0.019\;2 $ $ 0.021\;5 $ $ 0.023\;7 $ $ 0.013\;7 $ $ 0.025\;5 $ $ 0.020\;4 $ $ 0.020\;9 $ $ 0.015\;0 $ 组合赋权 $ 0.044\;9 $ $ 0.039\;5 $ $ 0.027\;0 $ $ 0.028\;6 $ $ 0.040\;5 $ $ 0.014\;3 $ $ 0.035\;5 $ $ 0.023\;3 $ $ 0.032\;1 $ $ 0.015\;2 $
下载: 导出CSV
-
[1] 铁道技术监督编辑部. 新时代交通强国铁路先行规划纲要[J]. 铁道技术监督,2020,48(9):1-6,24. DOI: 10.3969/j.issn.1006-9178.2020.09.001 [2] 孙永福,吴 昊,林晓言,等. 铁路建设项目综合评价指标体系与方法[J]. 铁道学报,2023,45(9):1-11. DOI: 10.3969/j.issn.1001-8360.2023.09.001 [3] 刘国梁,姚洪磊,解辰辉,等. 基于层次分析法的铁路网络安全检查评价方法研究[J]. 铁路计算机应用,2023,32(11):6-10. DOI: 10.3969/j.issn.1005-8451.2023.11.02 [4] 郑晓波. 基于AHP的铁路信息系统风险评价指标体系[J]. 中国安全科学学报,2020,30(S1):139-145. DOI: 10.16265/j.cnki.issn1003-3033.2020.S1.025. [5] 陈 路. 熵权法在信息安全风险评估中的应用[J]. 信息系统工程,2021,34(9):62-64. [6] 顾兆军,李怀民,丁 磊,等. 基于组合权重的工控系统安全形式化分析方法[J]. 计算机仿真,2022,39(12):422-428. DOI: 10.3969/j.issn.1006-9348.2022.12.078 [7] 刘彦麟,李 琪,吕晓艳,等. 基于层次分析法的铁路旅客换乘方案选择权重研究[J]. 铁路计算机应用,2019,28(11):9-12. DOI: 10.3969/j.issn.1005-8451.2019.11.003 [8] 邱菀华. 管理决策与应用熵学[M]. 北京:机械工业出版社,2002.
计量
- 文章访问数: 98
- HTML全文浏览量: 28
- PDF下载量: 30
