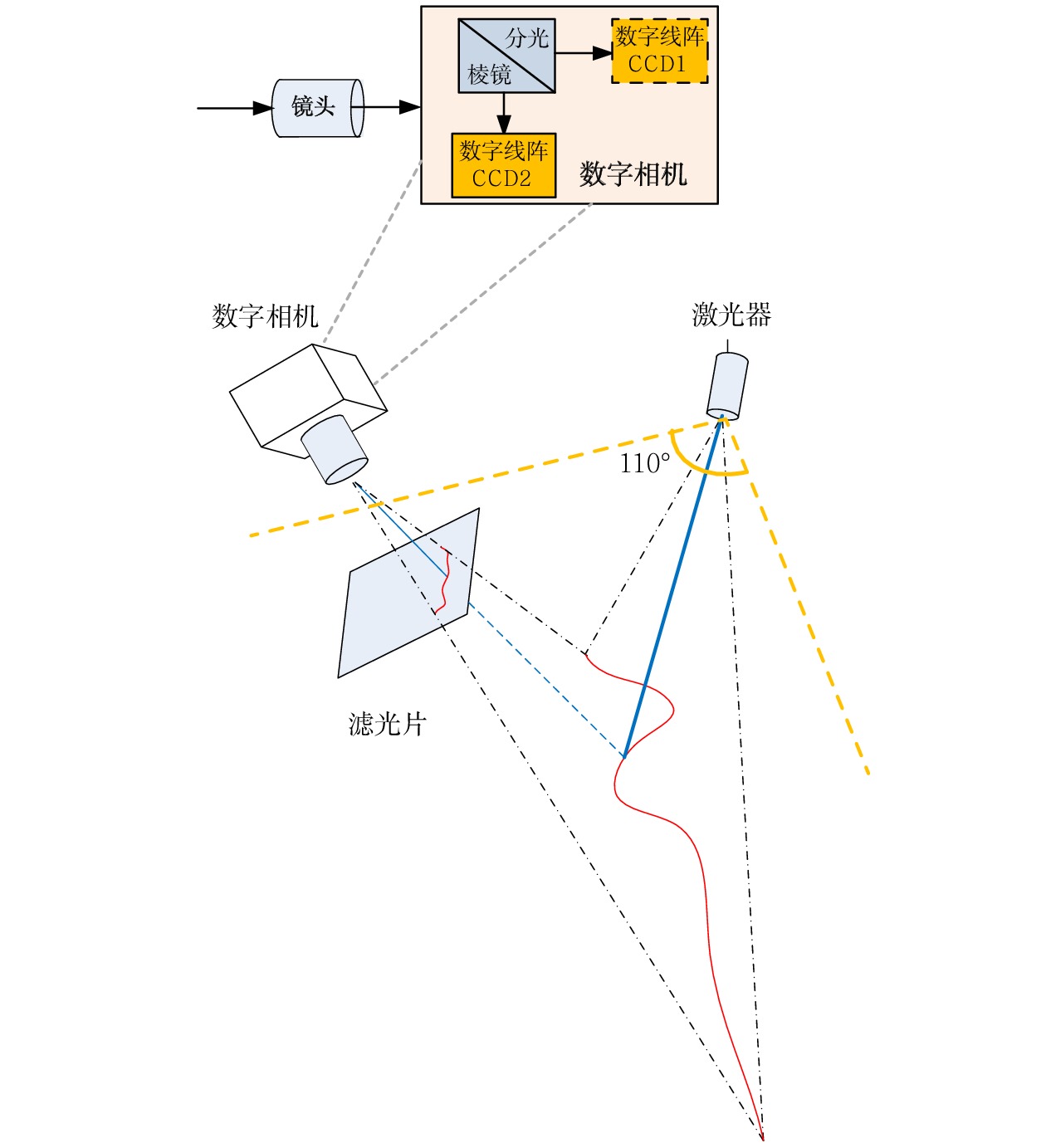
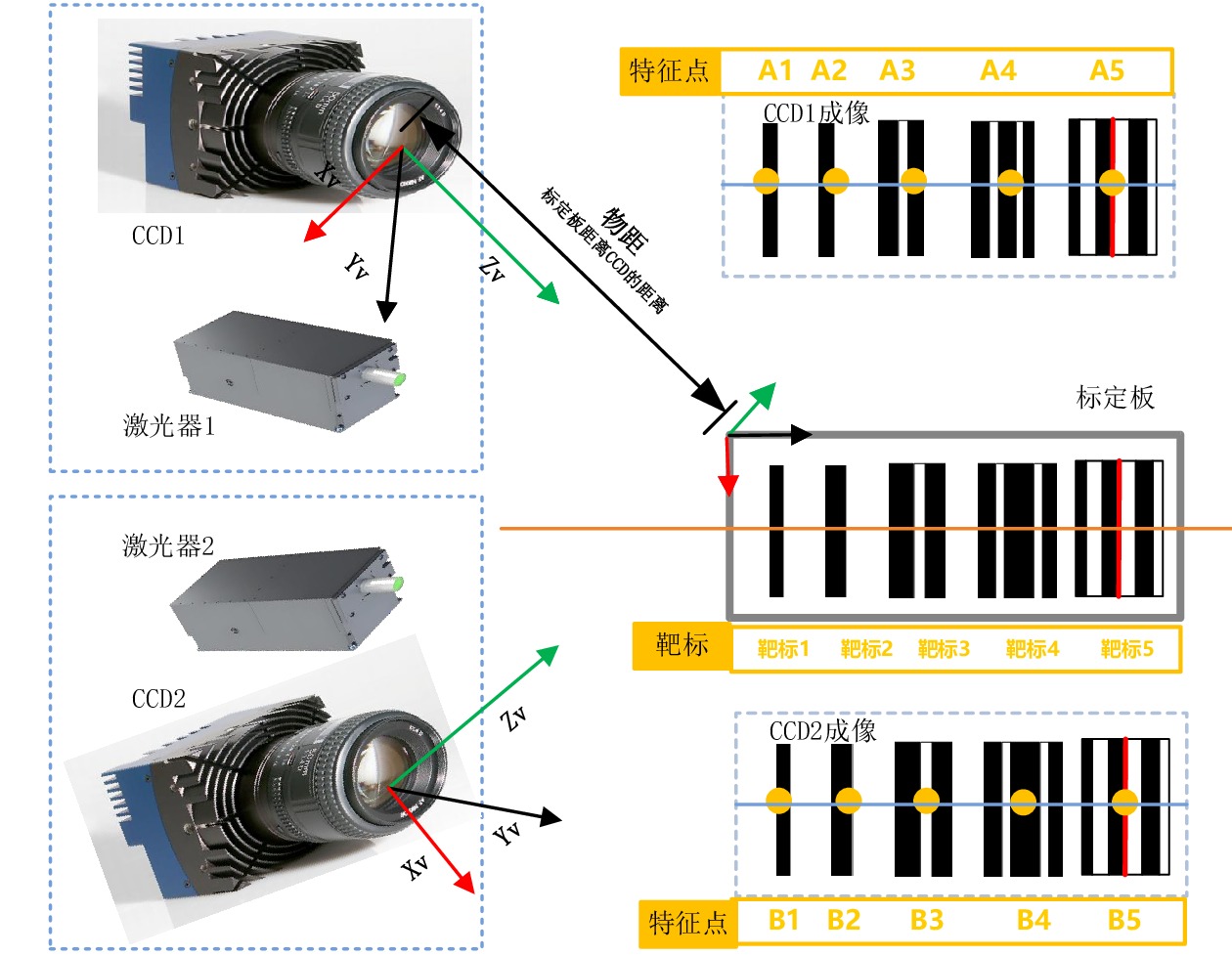
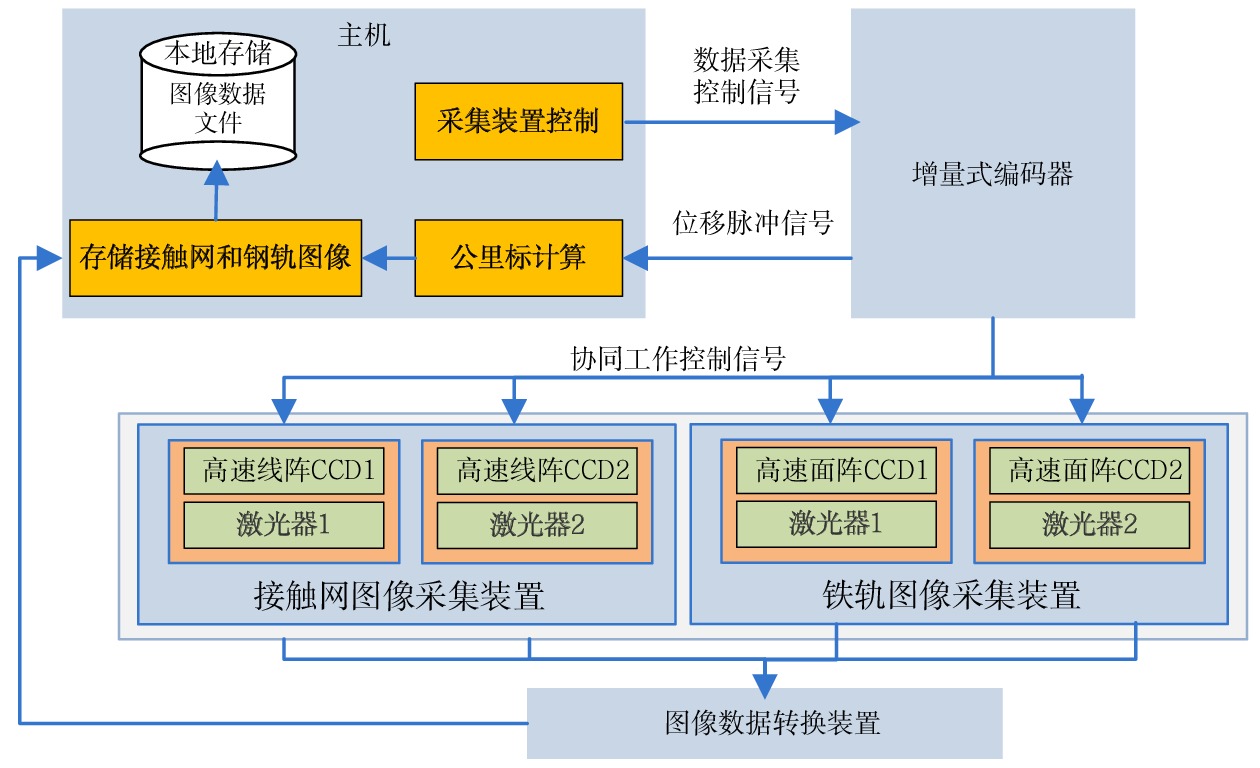
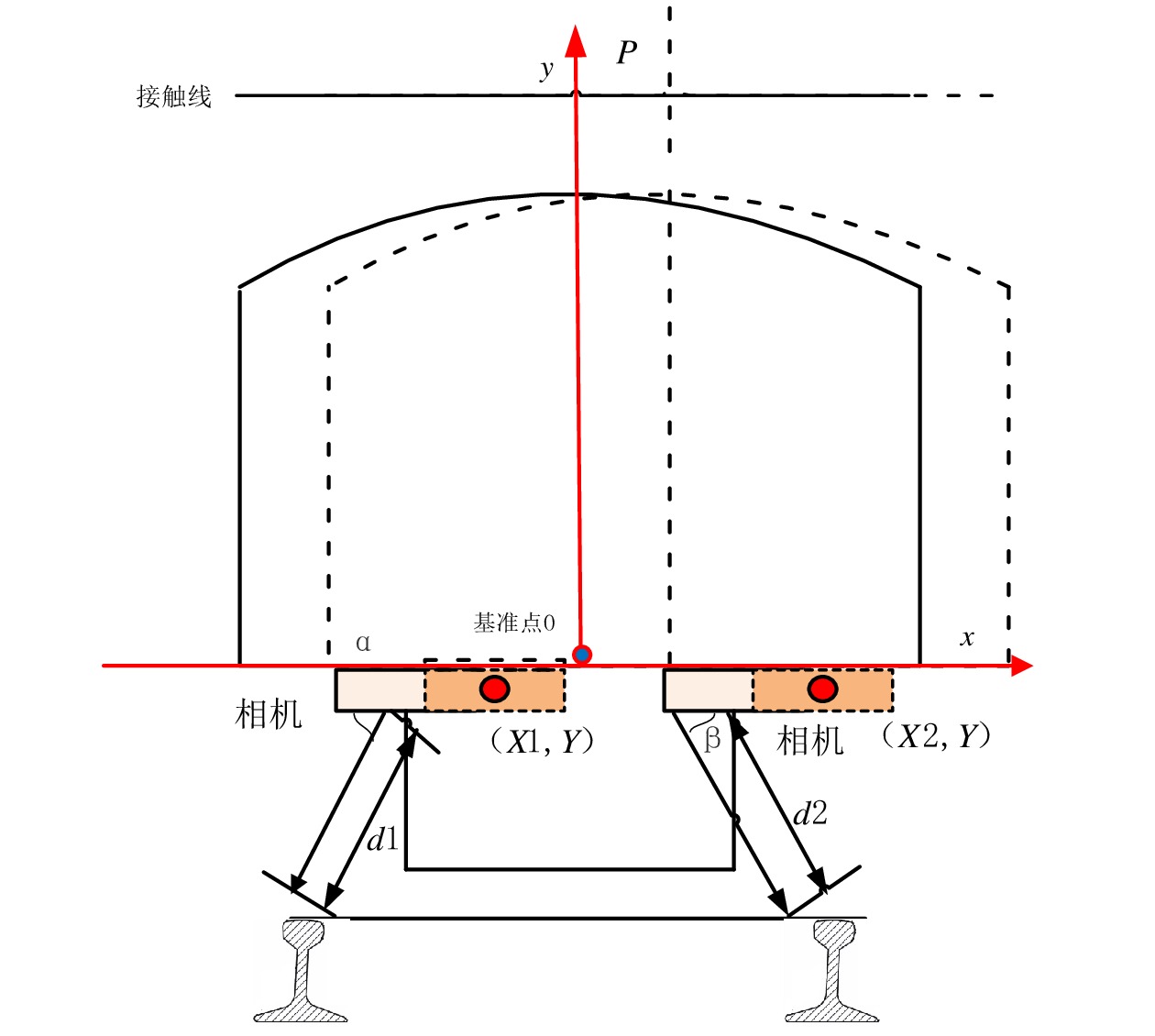
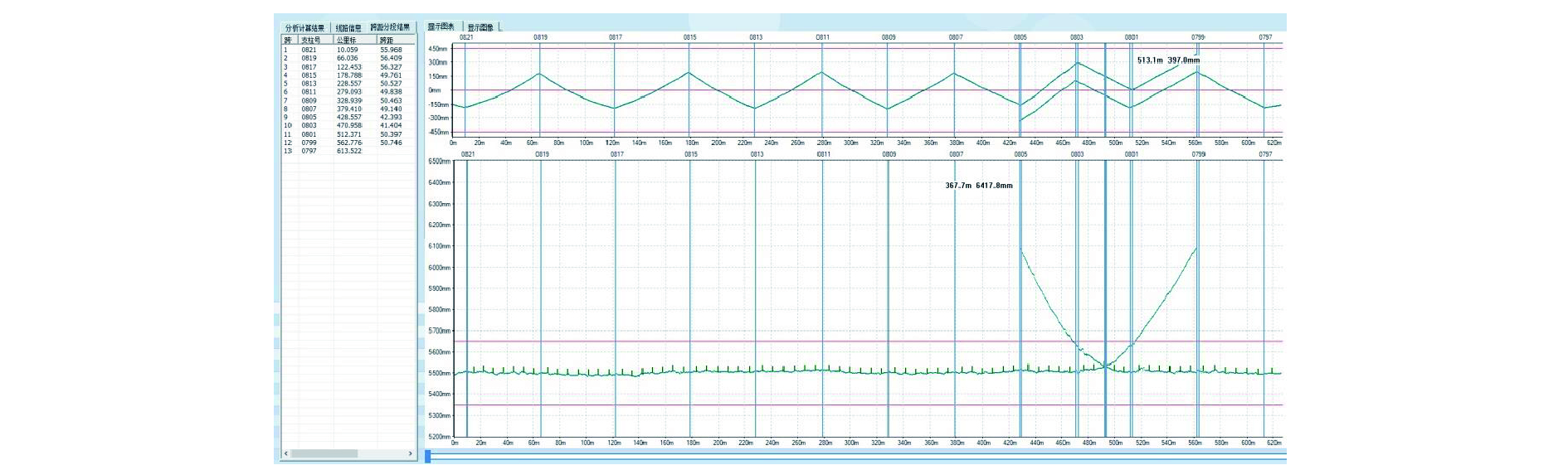
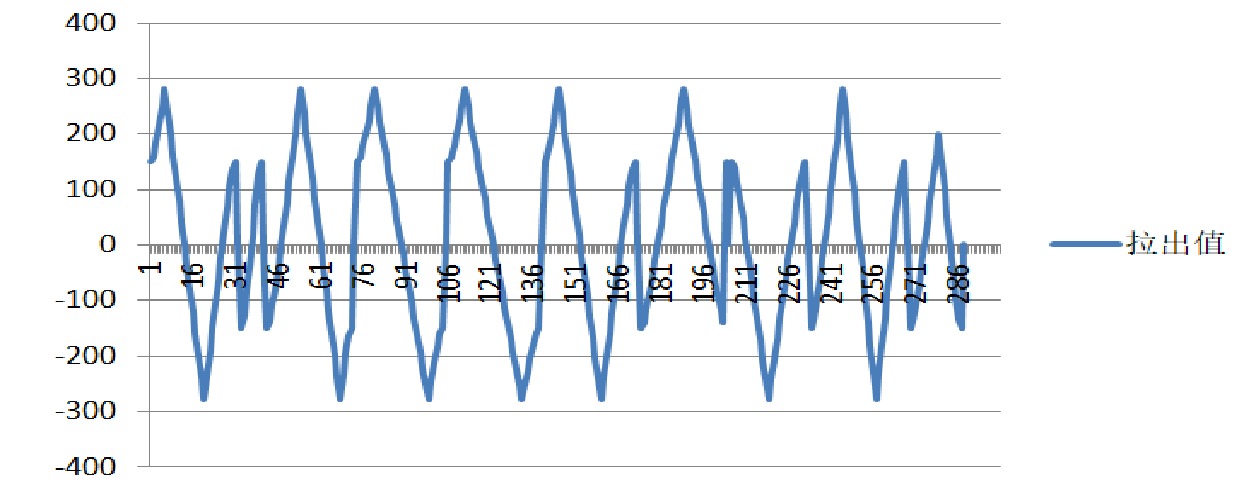
Dynamic detection system for geometric parameters of overhead contact system based on binocular 3D vision technology
-
摘要:
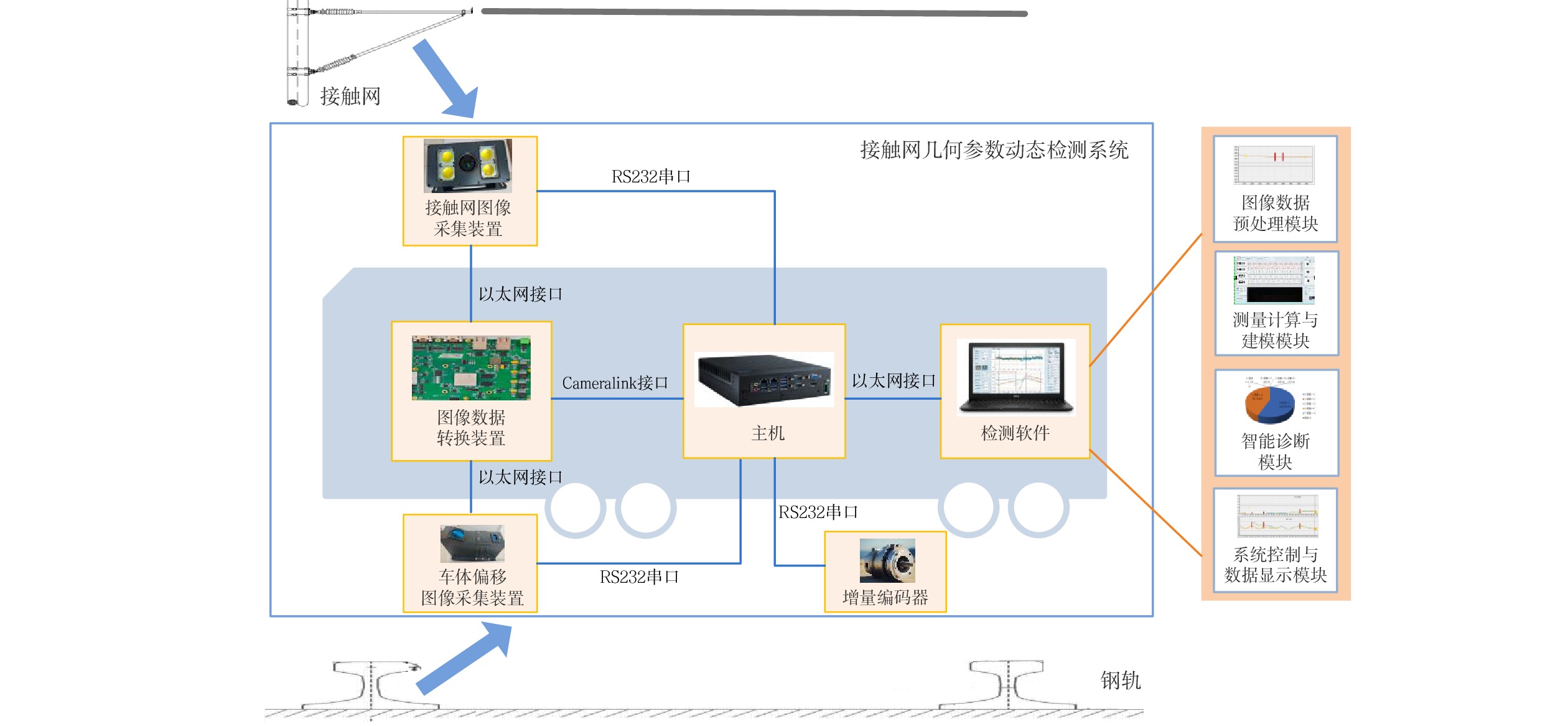
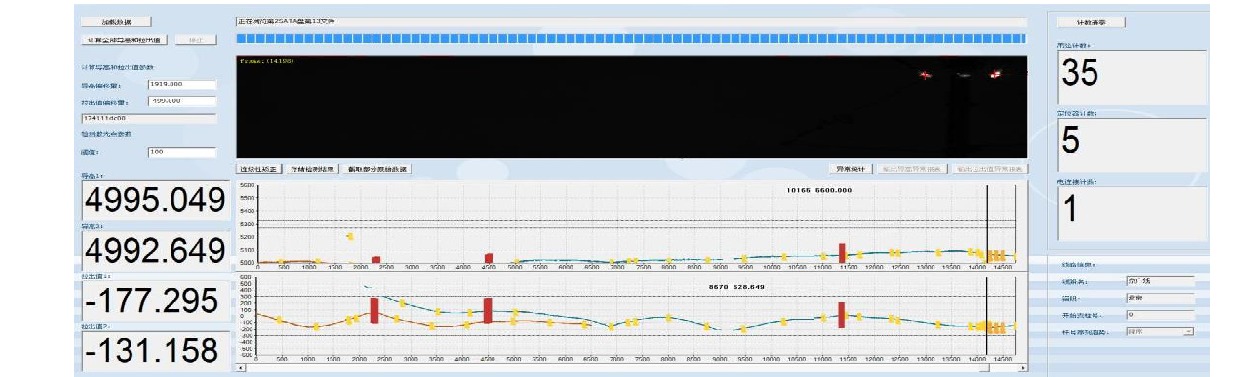
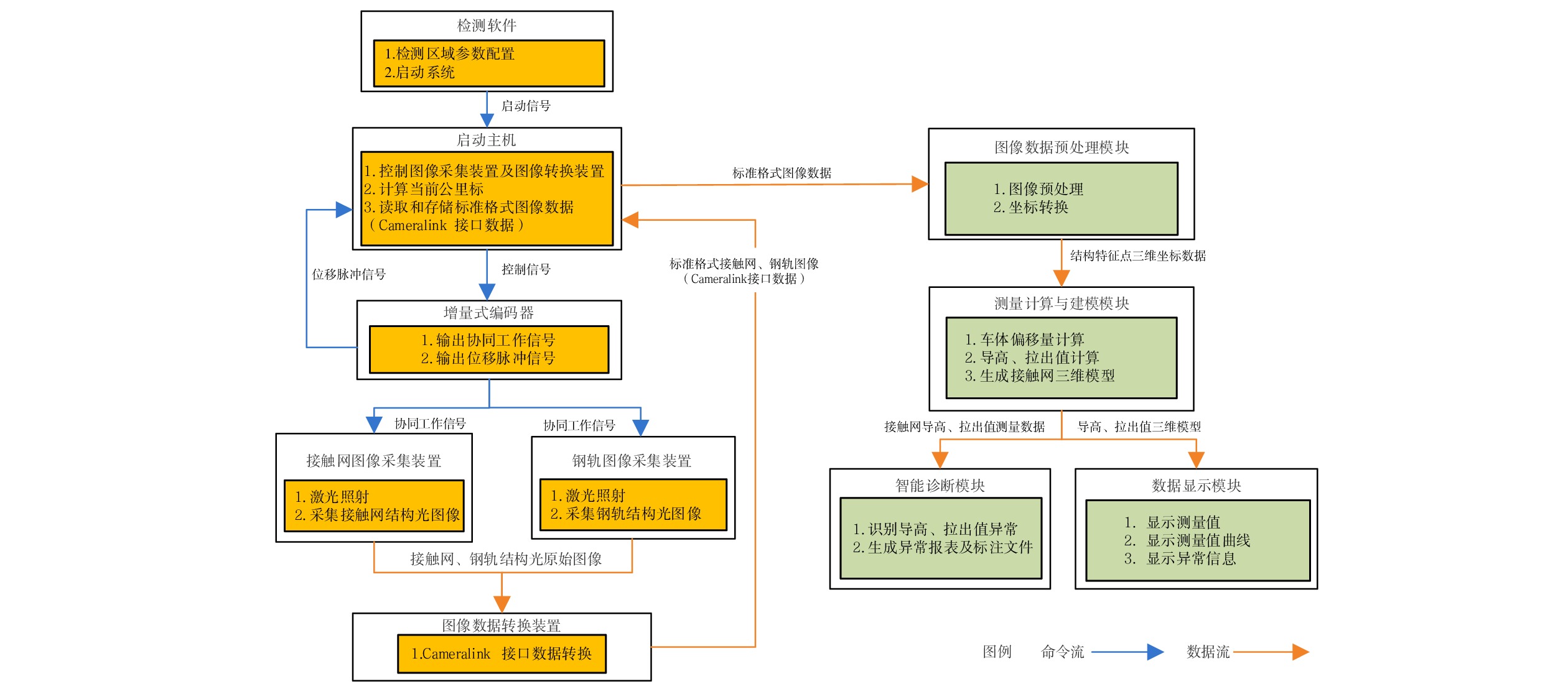
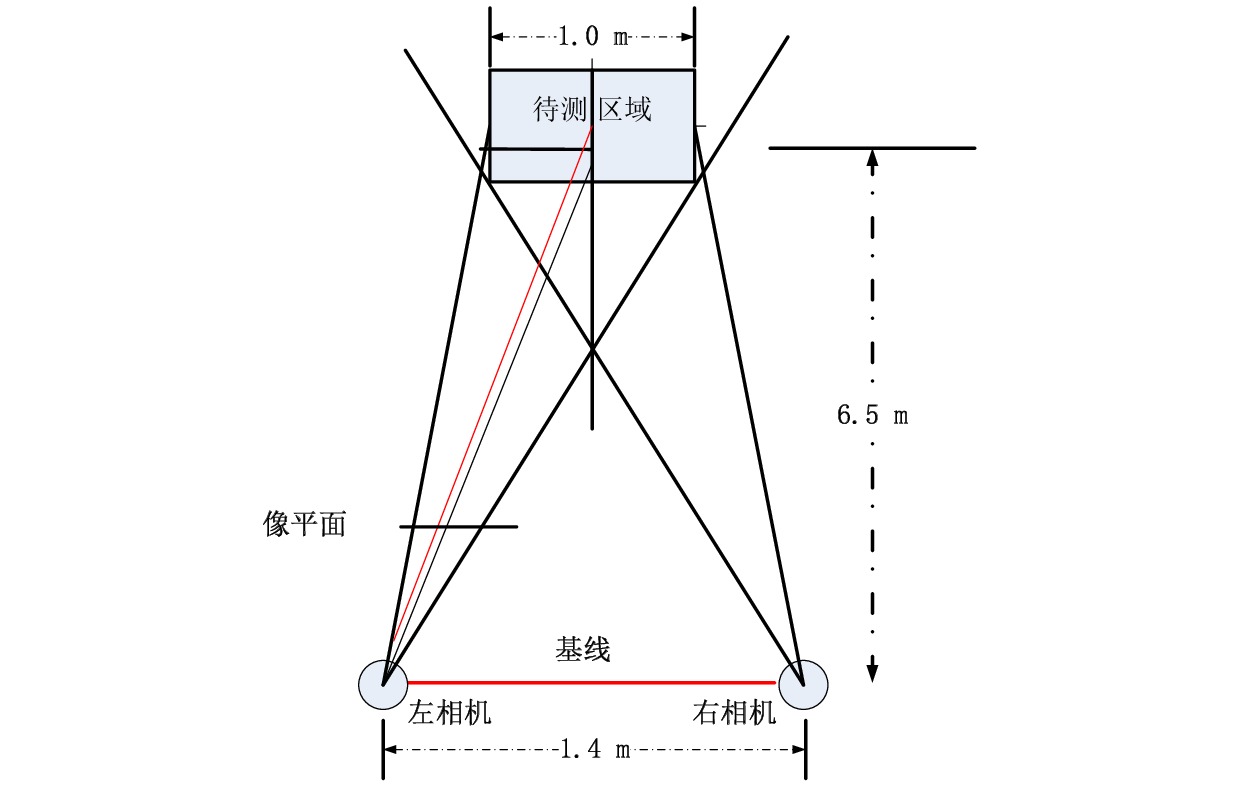
针对目前接触网几何参数检测设备工作效率低、精度不高的问题，采用双目3D视觉成像、结构光图像采集和图像处理等技术，研制了接触网几何参数动态检测系统。该系统主要由接触网图像采集装置、车体偏移图像采集装置、增量式编码器、图像数据转换装置、主机及检测软件组成，可随不同车载平台以0～120 km/h速度运行，能够在强光、低照度等天气条件下实现接触网导高、拉出值的动态非接触式检测，自动识别触网导高、拉出值异常，生成指导接触网精调和日常巡检所需的异常报表和标注文档。系统设备轻便、易于安装，并提供了有效的标定方法。在实验室搭建测试平台，进行导高、拉出值测试和车体振动位移修正测试，并在北京地铁某运营线路上进行初步动态测试。测试结果表明，该系统能够稳定地动态采集高清图像，接触网导高、拉出值测量精度误差低于5 mm，能够满足铁路、地铁和轻轨等接触网新建施工精调作业和运营线路接触网日常巡检作业需要。
Abstract:To deal with the low efficiency and low accuracy of current contact network geometric parameter detection equipment, a dynamic detection system of OCS geometric parameters has been developed using binocular 3D vision imaging, structured light image acquisition, and image processing. This system mainly consists of a OCS image acquisition device, a carboy offset image acquisition device, an incremental encoder, an image data conversion device, a host, and detection software. Installed on a vehicle at a speed of 0～120 km/h, it can achieve dynamic non-contact detection of the OCS's height and pull-out values and under strong light or low light, and automatically identify anomalies in the height and pull-out values of the OCS, generate anomalies report and annotated document to guide the fine adjustment and daily inspection of the OCS. Its equipment is lightweight, easy to install, and has effective calibration methods. A testing platform is built in the laboratory to conduct tests on lead height, pull-out value, and vehicle vibration displacement correction, and conducted preliminary dynamic tests on a operating line of the Beijing subway. The test results show that the system can stably and dynamically collect high-definition images, with measurement accuracy errors of less than 5 mm for the height and pull-out values of the overhead contact system. It can meet the needs of precision adjustment operations for newly constructed OCSs of railway, subway, or light rail lines as well as daily inspection operations for the OCSs of operating lines.
-
基于全球导航卫星系统（GNSS，Global Navigation Satellite System）的位移监测技术具有高精度、全天候、数据处理自动化等优势，在铁路基础设施安全监测方面的应用具有较大优势。但在正常运营期间，铁路线路周边处于封闭状态，造成铁路GNSS监测站（简称：监测站）安装完成后现场维护困难。因此，对监测站的GNSS观测数据质量提出了严格要求，在排查故障时，需要从数据角度进行分析，而不依赖于人员前往现场进行排查。GNSS观测数据的质量作为影响最终解算精度的重要因素之一，能有效反映监测设备在观测过程中存在的问题。
在现有的GNSS接收机（当将GNSS接收机用于监测用途时，一般称之为监测站）观测数据的质量分析中，数据质量指标有多种，评估方法各异 [1-2]。美国卫星导航系统与地壳形变观测研究大学联合体（UNAVCO，University NAVSTAR Consortium）研发的TEQC软件是广泛应用的GNSS数据质量分析软件之一[3]，采用了数据完整率、多路径误差、周跳比、载噪比等数据指标；国际GNSS服务（IGS，International GNSS Service）组织在评价IGS基准站数据质量时，采用了观测数据数目、周跳比、L1多路径误差与L2多路径误差共4项数据指标[4]；张宁等人[5]以数据完整率、多路径误差、信噪比和周跳比，结合可见卫星数、数据连续性统计做为数据指标，对国际GNSS服务（IGS，International GNSS Service）北京房山站的多系统GNSS观测数据进行了质量评估；程军龙等人[6]从载噪比、多路径误差及观测噪声3个方面评估了北斗三号全球卫星导航系统（简称：北斗三号）的观测数据质量，证明了北斗三号的观测数据比北斗二号区域卫星导航系统的观测数据的数据质量更高；Renhai Mu等人[7]及Houzhe Zhang等人[8]基于数据完整率、多路径误差、载波相位噪声等指标，分析了北斗三号观测数据的数据质量。
GNSS观测数据质量评价指标较多，而过多的指标并不能较好地提供有效信息，也有专家学者对此进行了研究。魏勇等人[9]使用TOPSIS（Technique for Order Preference by Similarity to Ideal Solution）综合评价模型对IGS和国际GNSS监测评估系统（IGMAS，International GNSS Monitoring & Assessment System）的多处基准站的观测数据，从数据完整性、数据有效率、伪距多路径、信噪比及周跳比5个指标进行了综合分析，给出了数据质量评价结果。但TOPSIS综合评价模型得出的是一种相对评价，只对样本进行内部优劣评价，不同样本间评价结果不可比[10]。
综上，当前大部分研究都是针对地基增强基准站的原始观测数据进行分析，尚缺乏对监测站GNSS观测数据的质量分析，数据完整率、周跳比、多路径误差值等指标对GNSS观测数据的数据质量进行各项指标的单项评估[11]，以及TOPSIS等方法的相对综合评估，存在一定局限。本文旨在综合数据完整率、多路径误差值、周跳比这3个常用的GNSS观测数据质量评价指标，基于监测站的GNSS观测数据，在多个数据质量评价指标与最终需要的坐标解算结果精度间建立预测模型，以预测的坐标解算精度作为监测站GNSS观测数据质量的评价标准，进行绝对性评价。
1 选取的GNSS观测数据质量指标
1.1 数据完整率
数据完整率是指在1个观测时段内、一定的采样率条件下，GNSS接收机实际观测到的历元数与理论应观测到的历元数的比值。公式为
$$ {{{D}}_{\text{I}}}{\text{ = }}\dfrac{{{N_{have}}}}{{{N_{expt}}}} \cdot 100{\text{% }} $$ (1) 其中，
${{{D}}_{\text{I}}}$ 为数据完整率；$ {N_{have}} $ 为实际观测的历元数；${N_{expt}}$ 为理论应观测到的历元数，数据完整率值最大为100%，数值越大说明当前观测时段内GNSS接收机实际观测历元数越多，观测环境和运行状态越好。1.2 多路径误差
GNSS接收机在接收直接来自于卫星的信号时，由于附近物体对信号的反射与折射，造成干涉信号与卫星信号叠加，形成合成信号，这种使观测值发生偏差的现象叫多路径效应。多路径效应对伪距和载波相位观测值都有一定的影响 [12-13]，该效应导致的测距误差一般称为多路径误差。多路径误差一般采用伪距观测值与载波相位观测值的线性组合进行计算，计算接收到的2个频率信号的多路径误差，公式为
$$ \left\{ {\begin{array}{*{20}{c}} {MP1 = {\rho _1} - \dfrac{{{f_1}^2 + {f_2}^2}}{{{f_1}^2 - {f_2}^2}}{\varphi _1} + \dfrac{{2{f_2}^2}}{{{f_1}^2 - {f_2}^2}}{\varphi _2}} \\ {MP2 = {\rho _2} - \dfrac{{2{f_1}^2}}{{{f_1}^2 - {f_2}^2}}{\varphi _1} + \dfrac{{{f_1}^2 + {f_2}^2}}{{{f_1}^2 - {f_2}^2}}{\varphi _2}} \end{array}} \right. $$ (2) 其中，
$ MP $ 为多路径误差；$ \rho $ 为伪距观测量；$ f $ 为载波频率；$ \varphi $ 为载波相位观测量；$1、2$ 分别代表对应GNSS卫星的2个波段频率索引。多路径误差越小，说明GNSS接收机周围观测环境对信号反射与折射的影响越小。一般认为，当实际测量的MP1 > 0.35，MP2 > 0.45时，多路径效应对观测数据的精度影响不可忽略[14]。1.3 周跳比
发生周跳是指GNSS接收机在跟踪观测卫星时，由于环境遮挡或其他原因导致信号失锁，载波相位观测的整周计数不连续，进而发生跳跃的情况。周跳比是指GNSS接收机在一个观测时段内，载波观测值数与观测过程中发生周跳次数的比值，能有效反应载波相位观测值的质量情况。周跳情况可用周跳比表示，也可采用每千历元的周跳数CSR来表示，公式为
$$ CSR = \frac{{1\;000}}{{o/slps}} $$ (3) 式中，
$o$ 为载波观测值个数；$slps$ 为周跳次数。超过半数的IGS站的CSR平均值 < 5，即周跳比 > 200[15]。2 评价方法
本文采用多元线性回归方法中的岭回归分析法对监测站GNSS观测数据的多项数据质量指标进行分析，建立由数据质量指标至最终解算精度的预测模型，用于评价监测站的GNSS观测数据质量情况。
2.1 评价指标
2.1.1 指标选择
结合国内外GNSS数据质量分析软件常用的评价指标，同时，考虑到解算需要铁路GNSS监测参考站（简称：监测参考站）的参与，且监测站与监测参考站间的基线距离也是影响最终解算精度的重要因素之一，因此，本文选择监测站与监测参考站的数据完整率、多路径误差MP1、多路径误差MP2、周跳比，以及基线距离共9项指标进行综合评价。
2.1.2 评价指标数据处理
在基于岭回归分析法建模前，可对所选取的评价指标进行正向处理，保持评价指标的同趋势化。而选取的评价指标存在多路径误差及基线距离2项逆向指标，可对这2项评价指标通过取倒数的方法，转换为正向评价指标。
2.2 岭回归分析法
岭回归分析法是一种基于最小二乘估计（OLS，Ordinary Least Square Estimation）法的改进方法，通过放弃最小二乘估计法的无偏性，以损失部分信息、降低精度为代价，获取回归系数更为符合实际情况的方法，能够有效解决数据间多重共线性问题，降低多重共线性对模型稳定性的影响，且对因变量未来的走势做出较为准确和稳定的预测[16]。因本文选取的评价指标间存在较强的共线性，故采用岭回归分析法建立模型。
最小二乘估计法公式为
$$ \mathop {\boldsymbol{X}}\limits^ \wedge = {({{\boldsymbol{A}}^{\boldsymbol{T}}}{\boldsymbol{A}})^{ - 1}}{{\boldsymbol{A}}^{\boldsymbol{T}}}{\boldsymbol{L}} $$ (4) 式中，
$\mathop {\boldsymbol{X}}\limits^ \wedge$ 为最小二乘法的估计向量；${\boldsymbol{ A}}$ 为解释变量组成的系数矩阵；${\boldsymbol{L}}$ 为观测向量。但在多元线性回归时，矩阵${{\boldsymbol{A}}^{\boldsymbol{T}}}{\boldsymbol{A}}$ 可能因解释变量间存在相关性导致奇异，从而无法求逆。岭回归分析法公式为
$$ \mathop {\boldsymbol{X}}\limits^ \wedge = {({{\boldsymbol{A}}^{\boldsymbol{T}}}{\boldsymbol{A}} + k{\boldsymbol{I}})^{ - 1}}{{\boldsymbol{A}}^{\boldsymbol{T}}}{\boldsymbol{L}}{\text{ }}(k > 0) $$ (5) 式中，
$k$ 为岭系数；${\boldsymbol{I}}$ 为单位矩阵。岭回归在${{\boldsymbol{A}}^{\boldsymbol{T}}}{\boldsymbol{A}}$ 加上$k{\boldsymbol{I}}$ 后使得矩阵满秩，因此可逆。k越大，使得模型方差${({{\boldsymbol{A}}^{\boldsymbol{T}}}{\boldsymbol{A}} + k{\boldsymbol{I}})^{ - 1}}$ 越小，但最终估计值会更加偏离真实值，模型偏差越大，因此，岭回归分析法的关键在于找到一个合理的岭系数以平衡模型的方差和偏差。一般将$k$ 的初始值设为0，以一定的步长增大，并根据已有用于建模的样本数据，可得到不同$k$ 值时各解释变量的系数，即模型的回归系数，以此绘制岭迹曲线。当各个解释变量的回归系数都趋于稳定时的最小岭系数值即为最优岭系数。3 应用分析
3.1 实验数据选择
实验选取浩吉（浩勒报吉—吉安）重载铁路沿线一处边坡的GNSS监测工点，工点布设有1处监测参考站及8处监测站，用于监测该边坡三维坐标的变化值。其中，监测参考站设立在边坡旁一处稳固位置，8处监测站均设立在边坡易发生形变的位置。
本文选取8处监测站（290D、290F、2911、2912、2913、2914、2915、2916）的7个观测时段（即观测时段a、b、c、d、e、j、n，每时段时长为1 h）的GNSS观测数据进行分析，将其中5个连续观测时段（a～e）的GNSS观测数据作为样本数据用于建立模型，余下2个间隔的观测时段（j、n）的GNSS观测数据用于模型校验。
3.2 实验数据建模
根据2.1中选择的评价指标，将监测站数据完整率（
$ {x_1} $ ）、正向处理后的监测站多路径误差$MP1'$ （$ {x_2} $ ）和$MP2'$ （$ {x_3} $ ）、监测站周跳比（$ {x_4} $ ）、监测参考站数据完整率（$ {x_5} $ ）、正向处理后的监测参考站多路径误差$MP1'$ （$ {x_6} $ ）和$MP2'$ （$ {x_7} $ ）、监测参考站周跳比（$ {x_8} $ ）、正向处理后的基线距离（$ {x_9} $ ）这9个解释变量作为自变量。将表征监测站最终坐标解算误差的均方根（RMS，Root Mean Square）（即坐标解算精度）作为岭回归分析法的因变量，进行建模。（1）通过自动化形变监测解算软件HCMonitor，可解算得到监测站三维坐标结果的RMS，使用GNSS观测数据质量分析软件TEQC处理得到所有8个监测站及监测参考站7个时段的观测数据完整率、MP1、MP2及周跳比值。由此，得到模型的所有因变量和自变量数据。由于篇幅有限，本文只列出8个监测站及1个监测参考站在a时段的观测数据质量分析结果，如表1所示。
表 1 监测站观测数据质量分析成果监测站和监测参考站 观测数据完整率 MP1 MP2 周跳比 基线距离/m RMS/mm 监测站290Da 96 0.42 0.67 72 93.7 10.4 监测站290Fa 99 0.42 0.94 279 67.1 12.3 监测站2911a 95 0.39 0.54 327 37.3 11.6 监测站2912a 99 0.4 0.51 153 93.9 10.1 监测站2913a 97 0.39 0.6 377 73.7 9.9 监测站2914a 100 0.39 0.53 3099 65.8 9.2 监测站2915a 100 0.29 0.47 3307 158.5 8.4 监测站2916a 97 0.81 0.63 121 199.1 17.1 监测参考站 99 0.31 0.52 3061 — — （2）为证明选取的评价指标间存在较强的共线性，对8个监测站、5个检测时段的观测数据质量分析指标进行共线性诊断，采用特征根判定法[17]，结果如表2所示。
表 2 共线性诊断结果维 特征根 条件指数 方差比例 （常量） $ {x_1} $ $ {x_2} $ $ {x_3} $ $ {x_4} $ $ {x_5} $ $ {x_6} $ $ {x_7} $ $ {x_8} $ $ {x_9} $ 1 9.17 1.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 0.00 2 0.51 4.25 0.00 0.00 0.00 0.00 0.48 0.00 0.00 0.00 0.00 0.00 3 0.20 6.81 0.00 0.00 0.00 0.01 0.00 0.00 0.00 0.00 0.00 0.52 4 0.06 12.11 0.00 0.00 0.05 0.05 0.11 0.00 0.00 0.00 0.01 0.03 5 0.04 15.38 0.00 0.00 0.25 0.10 0.09 0.00 0.00 0.00 0.00 0.01 6 0.02 21.42 0.00 0.00 0.55 0.69 0.00 0.00 0.00 0.00 0.00 0.34 7 0.01 43.66 0.00 0.03 0.06 0.02 0.00 0.00 0.00 0.00 0.00 0.02 8 0.00 131.68 0.00 0.19 0.03 0.02 0.09 0.01 0.01 0.00 0.00 0.04 9 0.00 137.25 0.00 0.77 0.02 0.11 0.21 0.00 0.00 0.01 0.01 0.04 10 0.00 1788.96 1.00 0.00 0.03 0.02 0.00 0.99 0.99 0.99 0.97 0.00 根据特征根判定法原理，当所有特征根中有至少1个特征根接近于0，则说明变量间一定存在多重共线性，同时，当条件指数大于100时，认为变量间存在强共线性关系。表2中3个特征根接近于0，且最大的条件指数为1788.96，远大于100，表明这些自变量间存在着多重共线性问题，适合用岭回归分析法预测模型进行数据处理。
（3）岭回归分析法预测模型方程为
$$ \begin{aligned} & \\ P_{\rm{RMS}} = &{a_1}{x_1}{\text{ + }}{a_2}{x_2} + {a_3}{x_3} + {a_4}{x_4}{\text{ + }}{a_5}{x_5}{\text{ + }}\\&{a_6}{x_6}{\text{ + }}{a_7}{x_7}{\text{ + }}{a_8}{x_8} + {a_9}{x_9} + b \end{aligned} $$ (6) 式中，
${a}_{n}$ 为自变量系数，n=1，2，3，···，9；$ b $ 为常数。为确定模型岭系数，需要绘制岭迹图，如图1所示。由图1可知，当岭系数≥0.05时，各自变量回归系数值趋向稳定，因此，本文将岭系数选定为0.05。
（4）选定岭系数后，可得到模型自变量系数如表3所示。
表 3 模型自变量系数自变量系数 $ {a_1} $ $ {a_2} $ $ {a_3} $ $ {a_4} $ $ {a_5} $ $ {a_6} $ $ {a_7} $ $ {a_8} $ $ {a_9} $ $ b $ 数值 −0.036 −3.045 1.03 0.001 −0.172 −7.081 2.586 0.002 50.941 49.226 代入公式（6）中可得
$$ \begin{aligned} P_{\rm{RMS}} =& - 0.036\cdot{x_1}{\text{ }} - 3.045\cdot{x_2} + {\text{ }}1.030\cdot{x_3} +\\ &{\text{ }}0.001\cdot{x_4} - 0.172\cdot{x_5} {\text{ }} - 7.081\cdot{x_6}{\text{ }} +\\ & {\text{ }}2.586\cdot{x_7} +{\text{ }}0.002\cdot{x_8}{\text{ }} + {\text{ }}50.941\cdot{x_9} + 49.226 \\ \end{aligned} $$ (7) （5）使用统计分析软件SPSS对建立的模型进行拟合优度的检验，模型的均方根误差为1.372 mm， p 值小于显著性水平（0.01），说明建立的岭回归分析法预测模型总体显著，即模型各自变量对因变量的共同影响具有显著性。
3.3 数据验证
本文使用浩吉铁路边坡监测工点另外2个观测时段（j，n）的GNSS观测数据进行模型验证。将8台监测站在这2个观测时段的GNSS观测数据的数据完整率、多路径误差、周跳比、基线距离等数据代入公式（7）中，可得到模型预测的RMS，对比实际HCMonitor软件解算后得到的RMS，可得到模型的预测误差，如表4所示。根据表4计算得到，模型预测误差的均方根为1.1 mm，相对误差平均为13%，优于GNSS解算的常规误差3~5 mm，模型验证误差如图2所示。
表 4 模型验证误差表GNSS观测数据 HCMonitor 软件解算
得到的RMS/mm本文模型预测值/mm 误差值/mm 290Dj 7.8 8.1 -0.3 290Fj 7.1 8.7 −1.6 2911j 6.1 5.4 0.7 2912j 7.2 6.6 0.6 2913j 7.7 8.3 −0.6 2914j 6.0 4.9 1.1 2915j 5.6 4.2 1.4 2916j 6.6 8.1 −1.5 290Dn 8.3 9.7 −1.4 290Fn 8.6 9.9 −1.3 2911n 11.0 10.0 1.0 2912n 8.8 10.3 −1.5 2913n 10.1 10.6 −0.5 2914n 8.7 9.6 −0.9 2915n 7.4 8.6 −1.2 2916n 13.0 12.2 0.8 综上，基于建立的岭回归分析法预测模型，能够通过监测站GNSS观测数据质量的数据完整率、多路径误差及周跳比等指标值，较准确地预测到最终的坐标解算精度，并可以坐标解算精度值为综合评价指标，实现对监测站GNSS观测数据质量的绝对性评价，即不同监测站观测数据质量间的评价结果可比，不同观测时段间GNSS观测数据质量的评价结果可比，不同监测工点间观测数据质量的评价结果也可比。
4 结束语
本文综合考虑了GNSS观测数据质量分析的常用指标及铁路基础设施形变监测的特点，选定了多个指标，选取一处边坡监测工点的实际数据建立了岭回归分析法预测模型，检验了模型的合理性。同时，通过测试数据验证了模型从监测站GNSS观测数据质量指标至最终坐标解算精度间预测的可靠性，以坐标解算精度值为综合评价指标，可对监测设备观测数据质量进行绝对性评价。并且，此评价方法不受监测对象类型的影响，可用于评价铁路边坡、路基、桥梁等众多对象形变监测的GNSS观测数据。但是，采用此种评价方式也存在一些弊端，即在不同的环境或工点的情况下，需要获取新的样本数据进行重新建模。
-
表 1 实验室导高测量测试数据表
单位：mm 序号 人工实际测量的标定点导高 系统测量的标定点导高 误差 1 4000 4001.8 1.8 2 4383 4384.3 1.3 3 4800 4803.8 3.8 4 5800 5801.6 1.6 5 6000 6004.1 4.1 
下载: 导出CSV
表 2 实验室拉出值测量测试数据表
单位：mm 序号 标定点导高 方向 人工实际测量的
拉出值数据系统测量的
拉出值数据误差 1 4385 左 12.0 12.9 2.4 2 4385 左 133.5 135.4 1.9 3 4385 右 350.5 −354.5 4.0 4 6000 右 100 −103.8 3.8 5 6000 右 400 −404.8 4.8
下载: 导出CSV
表 3 实验室车体振动模拟实验中车体偏移测量装置测试数据表
序 号 运动方向（$ \mathit{\theta } $,a,b） 左轨初始坐标（X,Y） 左轨计算坐标（X,Y） 右轨初始坐标（X,Y） 右轨计算坐标（X,Y） 1 逆时针$ 1^\circ $，右10，下10 （−572.5，−415） （−572.585，−415.338） （572.5，−415） （ 572.8595 ，−415.336）2 顺时针$ 1^\circ $，右10，下10 （−572.5，−415） （−572.253，−415.249） （572.5，−415） （ 573.0345 ，−415.254）3 逆时针$ 1^\circ $，右10，上10 （−572.5，−415） （−572.552，−415.112） （572.5，−415） （ 572.7951 ，−415.098）4 顺时针$ 1^\circ $，右10，上10 （−572.5，−415） （−572.438，−414.845） （572.5，−415） （ 572.8119 ，−414.851）5 逆时针$ 1^\circ $，左10，下10 （−572.5，−415） （−572.574，−415.168） （572.5，−415） （ 572.6453 ，−415.162）6 顺时针$ 1^\circ $，左10，下10 （−572.5，−415） （−572.743，−414.874） （572.5，−415） （ 572.6724 ，−414.877）7 逆时针$ 1^\circ $，右10，上10 （−572.5，−415） （−572.584，−414.88） （572.5，−415） （ 572.5346 ，−414.872）8 顺时针$ 1^\circ $，左10，上10 （−572.5，−415） （−572.748，−414.719） （572.5，−415） （ 572.3645 ，−414.727）
下载: 导出CSV
-
[1] 邢继军,张 曼. 一种受电弓与接触网的接触力检测方法[J]. 铁路计算机应用,2008,17(6):15-17. DOI: 10.3969/j.issn.1005-8451.2008.06.005 [2] 张 平,张建辉,李平芳. 高速铁路接触网安全巡检系统[J]. 铁路计算机应用,2016,25(3):34-36. DOI: 10.3969/j.issn.1005-8451.2016.03.010 [3] 乔凯庆,汪海瑛,王 婧,等. 基于6C系统大数据分析的接触网零部件缺陷特征研究[J]. 中国铁路,2023(7):39-44. [4] 张 毅. 深度学习在接触网定位器缺陷检测中的应用[J]. 铁路计算机应用,2018,27(3):15-19. DOI: 10.3969/j.issn.1005-8451.2018.03.004 [5] 曹春生,王文昊,谢大鹏,等. 基于图像识别的接触网安全巡检系统[J]. 铁路技术创新,2023(6):50-54. [6] 陈 兵,朱泳标,邹 杨,等. 三维地质模型在铁路勘察中的应用[J]. 铁路技术创新,2022(4):77-81. [7] 汤友福,朱 挺. 线阵列CCD摄像技术在铁路检测领域的应用[J]. 铁路计算机应用,2004,13(5):23-25. DOI: 10.3969/j.issn.1005-8451.2004.05.010 [8] 于秋波,倪国政,王志锐. 城轨交通接触网安全在线监测系统[J]. 中国铁路,2024(3):50-56. -
期刊类型引用(3)
1. 刘彦. 农业科学院所无形资产评估方法研究. 现代商业研究. 2024(05): 23-25 . 
百度学术
2. 刘彦. 农业类科研院所中无形资产的评估方法研究. 商讯. 2024(10): 13-16 . 百度学术
3. 丁传琛. 数字经济背景下铁路数据资产定价方法研究. 铁道经济研究. 2024(06): 57-64 . 百度学术
其他类型引用(0)
计量
- 文章访问数: 34
- HTML全文浏览量: 22
- PDF下载量: 16
- 被引次数: 3
