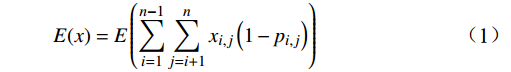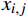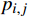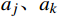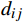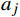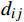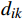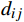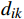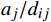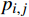随着我国经济的蓬勃发展，旅客的出行需求持续增长，特别是在节假日期间，旅客集中出行，导致热门线路的列车客流量激增，铁路运输能力紧张、供需矛盾凸显，形成了长短途出行需求争抢运力的态势。在假期返程的高峰时刻，面对紧迫的返工出行压力，部分旅客会选择购买短途车票，但实际乘车行程却远超过购票区间，即所谓的“买短乘长”。这样的行为导致列车上的旅客人数在列车运行途中不断累积，特别是在上下车旅客较多的客流大站，列车的乘降组织面临较大压力，极易造成列车超员停车事故（简称：超停），不仅严重干扰了后续列车的正常运行组织，也对车站的客运管理工作带来了较大的难度和挑战。

为保障动车组列车的运输安全，其超员上限通常设定为不超过定员的20%^[1-3]。因此，客运部门及各铁路局集团公司在客流高峰期需要在预售期内对所有列车的车票销售速度及剩余票额变化进行实时监控，通过设定阈值并严格卡控列车短途区间票额供给数量的方式，达到防止列车超停的目的。王元媛等人^[4-5]指出，旅客列车高峰期超员主要是由于列车无座席超员、短途车票超售和买短乘长超售导致的；汪建雄等人^[6-7]阐述了防止超停主要可采取的列车无座席上限控制、短途车票超售控制、指定区间停售等技术手段。

但由于旅客的买短乘长行为无法反映在旅客所购买车票的票面信息当中，售出的短途车票既包含实际短途出行的旅客，又包含买短乘长的旅客，且旅客的实际乘长区间也不固定，因此，无法准确计算列车在各区间的实际车内人数^[8-9]，常由一线工作人员凭借以往的客流规律和实际工作经验来判断短途票售出的阈值，无法实现客流精细化管理。

为此，本文提出一种基于高峰期热门出行目的地识别的旅客买短乘长行为预估模型。通过深入分析历史高峰期旅客出行规律，结合各城市等级的划分思路^[10]，分析列车途经的假期热门目的地城市客流吸引度，计算该车次购短途票旅客买短乘长的风险概率。

1   旅客买短乘长行为预估模型

1.1   数据集

本文选取2023年春运、“五一”和“十一”假期期间返程高峰期的热门方向列车客流数据进行建模，这是因为买短乘长行为主要出现在节后的客流高峰期。同时，由于旅客买短乘长时，往往需要在车上或到站以后进行补票，补票数据可用来判断真实的买短乘长行为。因此，本文采用返程高峰期的补票数据对实际买短乘长行为进行标定和验证。并且，考虑到高峰期超停列车主要集中在停站个数大于10站以上的动车组列车中，因此，以这些超停高风险车次数据为主进行建模。

1.2   高峰期热门目的地识别

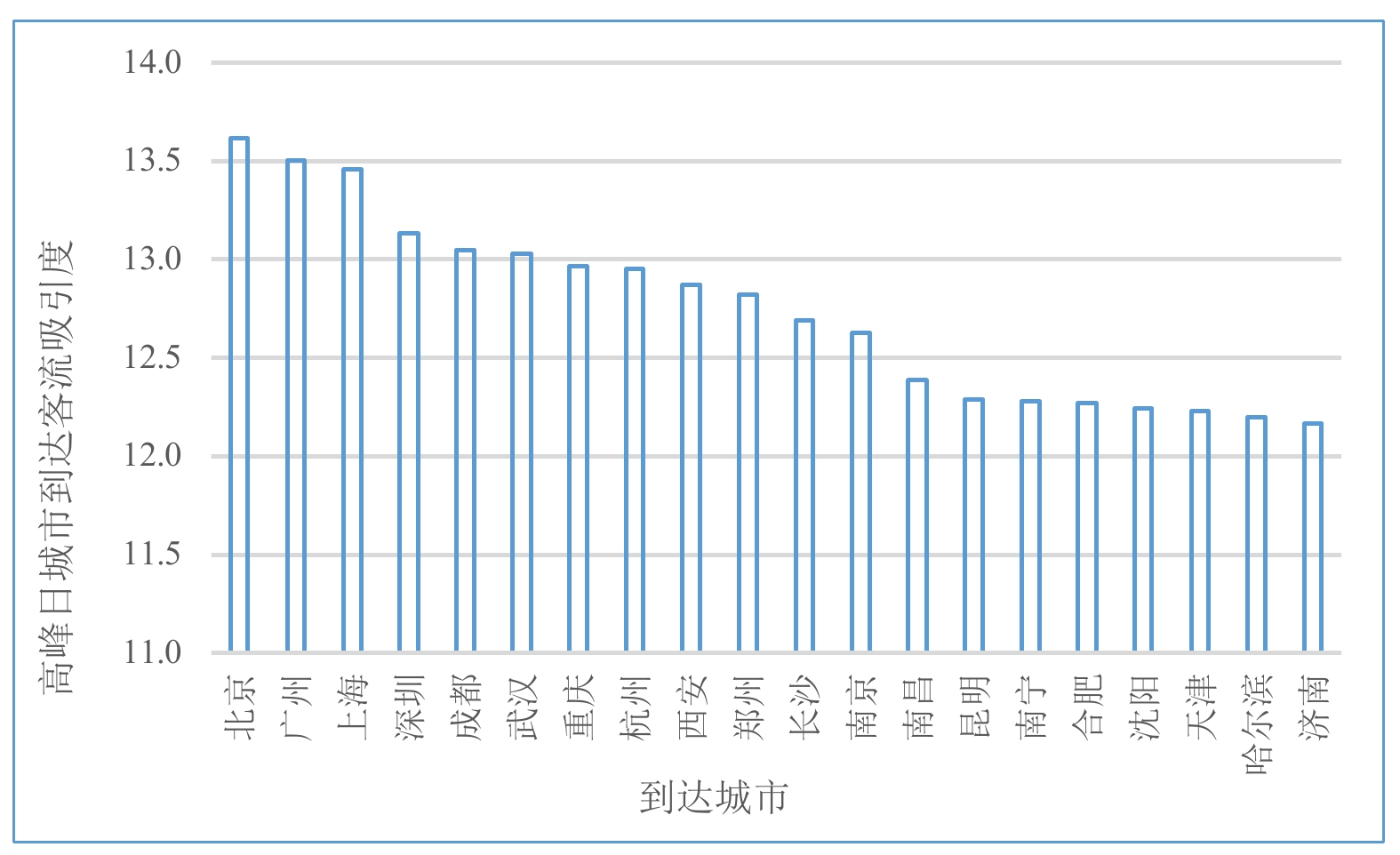
通过对高峰期不同城市的下车旅客人数取对数并标准化处理后，可得到衡量不同城市的客流吸引度，将其作为列车途径城市旅客下车概率的衡量指标，从而评判旅客到达列车各沿途城市的可能性，实现短途旅客买短乘长风险的预估。2023年春节、“五一”“十一”节后高峰日全国主要城市客流吸引度如图1所示。由图1可知，返程高峰期客流吸引度排名前5的城市分别是北京、广州、上海、深圳和成都，意味着高峰期开往这几个城市的列车上的旅客买短乘长概率最大。

图  1  2023年春节、“五一”“十一”节后高峰日全国主要城市客流吸引度

下载: 全尺寸图片 幻灯片

1.3   模型构建

以高峰期不同城市对客流吸引度的统计数据为基础，构建旅客买短乘长行为预估模型，高峰期超停高风险列车车内旅客买短乘长人数期望值为

式（1）中， i为上车站；j为下车站；n为列车的停站个数；$ {x}_{i,j} $为短途区间i到j的购票人数，是已知量，可根据售票情况计算得出；$ {p}_{i,j} $为实际出行概率，代表购买区间i到j车票的旅客中，实际出行时也在该区间上下车的概率，需要采用不同城市对客流的吸引度进行估算，估算方法为

式（2）中，$ {a}_{j}、{a}_{k} $分别表示车站j和k所在城市的客流吸引度，用历史高峰期客流量进行估算；$ {d}_{ij} $表示区间i到j的实际里程。

除城市客流吸引度$ {a}_{j} $的大小外，区间i到j的距离$ {d}_{ij} $及区间i到前方站k的距离$ {d}_{ik} $也是影响旅客买短乘长的重要因素。当$ {d}_{ij} $越短、$ {d}_{ik} $越长时，旅客买短乘长到车站k下车的概率就越低。因此，选择$ {a}_{j}/{d}_{ij} $作为车站j的客流分担率。区间i到j的客流分担率占区间i到所有前方站客流分担率之和的比例，就是旅客在区间i到j的实际出行概率。

2   模型验证与结果分析

2.1   模型验证

本文采用R语言构建旅客买短乘长行为预估模型并对该模型的准确性进行检验。R语言具有简单、开源及便于使用的特点，是进行大数据处理、数据统计与分析的常用工具之一^[11]。

（1）使用R语言从数据库中筛选出用于建模的主要数据，即节后高峰期终到方向为北京、上海、广州、深圳和成都市的停站数超过10个的动车组列车运营数据，一趟列车为一条样本数据。同时，计算列车各区间短途客流的补票量合计作为指标，评估车内买短乘长旅客的实际人数。

（2）估算列车途径所有城市的客流吸引度，并将列车时刻表数据中的开行里程带入到该模型中，计算列车所有区间的旅客实际出行概率$ {p}_{i,j} $。

（3）再根据各短途区间的实际购票人数和实际出行概率，估算出该趟列车的买短乘长人数占比，即预估买短乘长人数占实际乘车人数的比例，并与实际的补票人数占实际乘车人数的比例进行比较，计算该模型误差。

本文采用绝对误差与均方误差（MSE）这2个指标衡量该模型的误差。通过计算绝对误差在±5%以内的车次样本个数占整体的比例，计算结果的可接受程度；通过计算样本的均方误差来反映该模型的误差情况；同时将所有样本进行合计，作为衡量该模型整体的误差情况。模型的预测效果如表1所示。

表  1  旅客买短乘长行为预估模型预测效果

样本观察期	终到方向	样本个数	绝对误差在±5%以内样本占比	MSE
春节节后 高峰	北京	150	85.6%	0.19%
	广州	115	85.0%	0.23%
	成都	146	77.7%	0.29%
	上海	248	87.7%	0.19%
	深圳	106	77.1%	0.42%
“五一”节后 高峰	北京	157	88.5%	0.17%
	广州	112	91.1%	0.16%
	成都	163	84.0%	0.21%
	上海	245	86.2%	0.19%
	深圳	99	82.3%	0.29%
“十一”节后 高峰	北京	146	80.7%	0.38%
	广州	125	75.4%	0.35%
	成都	156	78.9%	0.31%
	上海	244	85.7%	0.24%
	深圳	104	70.7%	0.55%
整体合计		2316	83.4%	0.26%

下载: 导出CSV 

| 显示表格

2.2   结果分析

本模型的有效样本数为2316条。从表1可知，该模型在各观察期内、各主要热门城市的高准确度车次比例均高于70%，“五一”节后高峰期开往广州方向的列车准确度最高，高准确度车次占比达到91.1%；整体上该模型的MSE为0.26%，各观察期内、各主要热门城市的均方误差均小于0.6%。验证结果表明，该模型准确率基本达到可应用标准，根据列车当前短途票的售出情况和列车经由站，可提前对买短乘长旅客规模、各车站间车内超员人数、各站实际上下车人数进行预估，从而在事前对超停高风险列车进行预警。

2.3   实际应用情况

本模型在2024年“五一”运输高峰期间进行了试用，基于预售数据，代入本文模型，预估列车实际超员人数，提前判断列车超停风险，并及时采取措施进行预警和防控。在“五一”高峰期客流量创历史新高的同时，保障了运输组织的安全、有序，无列车超停事故发生。

3   结束语

本文研究了高峰期热门出行目的地城市客流吸引度与旅客买短乘长行为间的关系，并提出一种预估方法。通过分析历史高峰期客流数据，构建买短乘长行为预估模型，用于预测节后高峰期实际买短乘长的旅客比例，为高峰期列车超员人数预估和超停高风险列车事前预警提供一种有效的分析手段。经过高峰期数据实际验证，本模型整体预测结果的均方误差为0.26%，具有实际应用价值。

下一步，可引入更丰富的维度并进一步优化，例如，从产品端，引入列车上座率、席位复用率等指标衡量列车日常长短途旅客比例；通过分析旅客群体出行习惯，预判短途票旅客的买短乘长风险。通过多种维度综合衡量列车超停风险，从而提高模型预测精度和效率，为保障高峰期列车安全、平稳运营提供更准确的技术支撑。