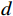User credit profile integrating SOM Neural network and K-means clustering algorithm
-
摘要:
为提高现阶段基于K-Means聚类算法的用户信用画像模型的准确性和实时性,提出一种融合自组织映射(SOM,Self-Organizing Map)神经网络与K-Means聚类算法的改进方法。通过SOM对用户数据进行降维和特征提取,直接获得最优聚类数目后再用K-Means算法进行聚类分析。通过真实在线借贷平台数据对所提方法进行验证,结果表明,该方法可提升用户信用画像分析的质量,更好地满足金融数据分析中对实时管理和风险控制的要求,为金融机构提供精准的决策支持。
-
关键词:
- 用户信用画像 /
- SOM神经网络 /
- K-means聚类算法 /
- 时间复杂度 /
- 风险控制
Abstract:To improve the accuracy and real-time performance of user credit profile models based on K-Means clustering algorithm, this paper proposed an improved method that integrated Self Organizing Map (SOM) neural network with K-Means clustering algorithm. The paper used SOM to reduce dimensionality and extract features from user data, directly obtained the optimal number of clusters, and then used K-Means algorithm for clustering analysis, validated the proposed method through real online lending platform data. The results show that the proposed method can improve the quality of user credit profile analysis, better meet the requirements of real-time management and risk control in financial data analysis, and provide accurate decision support for financial institutions.
-
数字化时代,用户信用画像已成为数据分析与商业策略不可或缺的重要工具,即利用用户的在线行为和交易习惯为其贴标签,提取用户群体的共性,可助力企业了解客户需求,降低营销成本,辅助风险控制等[1]。信用画像反映了用户的信用行为和风险水平,对于信贷审批、市场营销等多个领域的风险控制至关重要。
快速而准确的信用画像分析,可为金融机构提供实时的信用评估,从而作出更精准的贷款决策,降低潜在信贷风险[2]。因此,在用户信用画像分析中,时效性是不可忽视的重要因素。但目前已有的相关方法在处理大规模数据时,效率较为低下,在用户细分和行为特征提取方面还需要改进。因此,亟需开发效率更高、精度更高的算法以优化用户信用画像的构建与应用。
聚类算法作为一种重要的数据分析手段,被广泛应用于用户信用数据的分组和模式识别。传统的聚类算法(如K-Means)由于其简单性一直被广泛使用,但该算法需要多次迭代评估以确定最优的聚类个数。谱聚类算法[3]和深度学习方法[4]可用于提取数据的高级特征表示,为聚类提供更加丰富的特征空间,但需要大量的训练数据,在训练和推理过程中计算成本较高。上述方法皆无法满足风险控制中快速响应的需求[5]。自组织映射(SOM,Self-Organizing Map)神经网络是一种基于神经网络的无监督学习方法,通过构建一个低维网格来实现数据聚类,主要用于高维数据的初步聚类和可视化,能够自动将高维输入数据映射到低维空间,在保持数据拓扑结构的同时,揭示数据的内在结构[6]。
因此,本文提出一种以SOM神经网络(简称:SOM)优化K-Means的聚类算法,融合SOM自组织特性与K-Means算法聚类效能,针对用户属性数据进行深度分析,从而准确提取与用户信用画像相关的精细化的用户标签,实现用户群体的精准划分,可对金融机构在信用评级、风险控制、贷款策略制定等方面提供支撑。
1 融合SOM与K-means的聚类算法及分析
1.1 SOM算法实现步骤
采用SOM进行初步聚类,将高维数据映射到二维空间并形成若干紧密区域,区域的个数即可作为K-Means算法聚类中心的初始值。SOM算法实现的步骤如下。
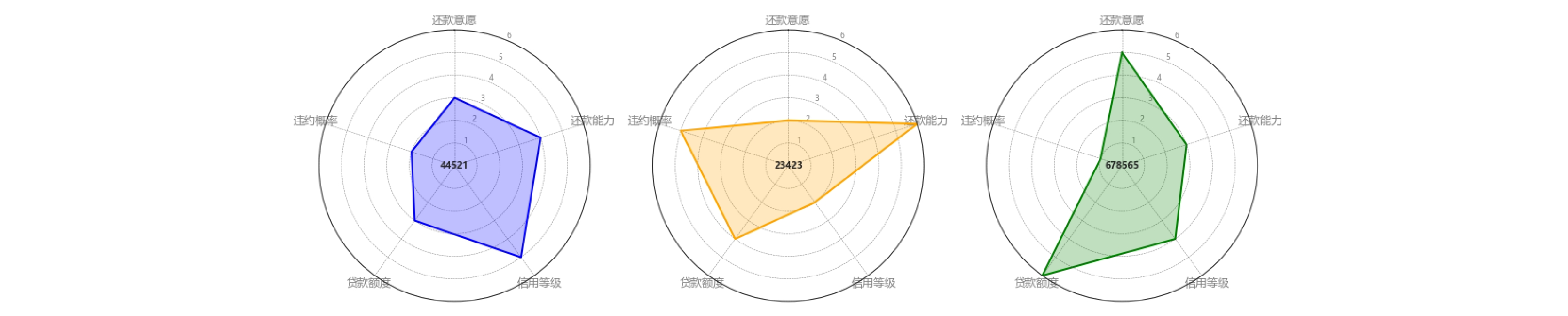
(1) 初始化网络参数:初始化一个由神经元组成的网络,每个神经元对应于数据空间中的一个点。第j个神经元的权重向量
{{\boldsymbol{W}}}_{j} 随机初始化,维度与输入数据X相同。例如,对n维输入向量\boldsymbol{X}=\left(x_1,x_2,\dots, x_n\right) ,神经元的权重向量表示为{{\boldsymbol{W}}}_{j}=\left({w}_{j1},{w}_{j2}, \dots ,{w}_{jn}\right) ,其中,{w}_{ji} 表示第j个神经元与输入向量X的第i个分量的距离。(2) 随机选取样本输入:从数据集中随机选择一个样本,作为网络输入。
(3) 寻找最匹配神经元:计算第j个神经元与输入样本向量
{\boldsymbol{X}} 的欧几里得距离d_{j\left(\boldsymbol{X}\right)} ,公式为{d}_{j\left({\boldsymbol{X}}\right)}=\sum _{i=1}^{n}{\left({x}_{i}-{w}_{ji}\right)}^{2} (1) 式(1)中,与输入样本距离最小的即为最匹配神经元
I({\boldsymbol{X}}) 。(4) 更新邻近神经元的权重:在找到最匹配神经元
I({\boldsymbol{X}}) 后,通过梯度下降公式更新该神经元及其邻近神经元的权重,公式为\Delta w_{ji}=\eta(t)\cdot T_{j,i(\boldsymbol{X})}(t)\cdot(x_i)-w_{ji} (2) 式(2)中,η(t)为学习率; Tj,i(X)(t)为神经元j和最匹配神经元
I({\boldsymbol{X}}) 之间的距离。(5) 判断SOM是否收敛:如果达到预定的迭代次数,或学习率η(t)下降到某个阈值以下,则认为算法已收敛,否则重复步骤(2)~(4)。
(6) 将SOM输出的特征区域数作为K-means算法中的聚类数目k。
1.2 基于SOM的初始聚类
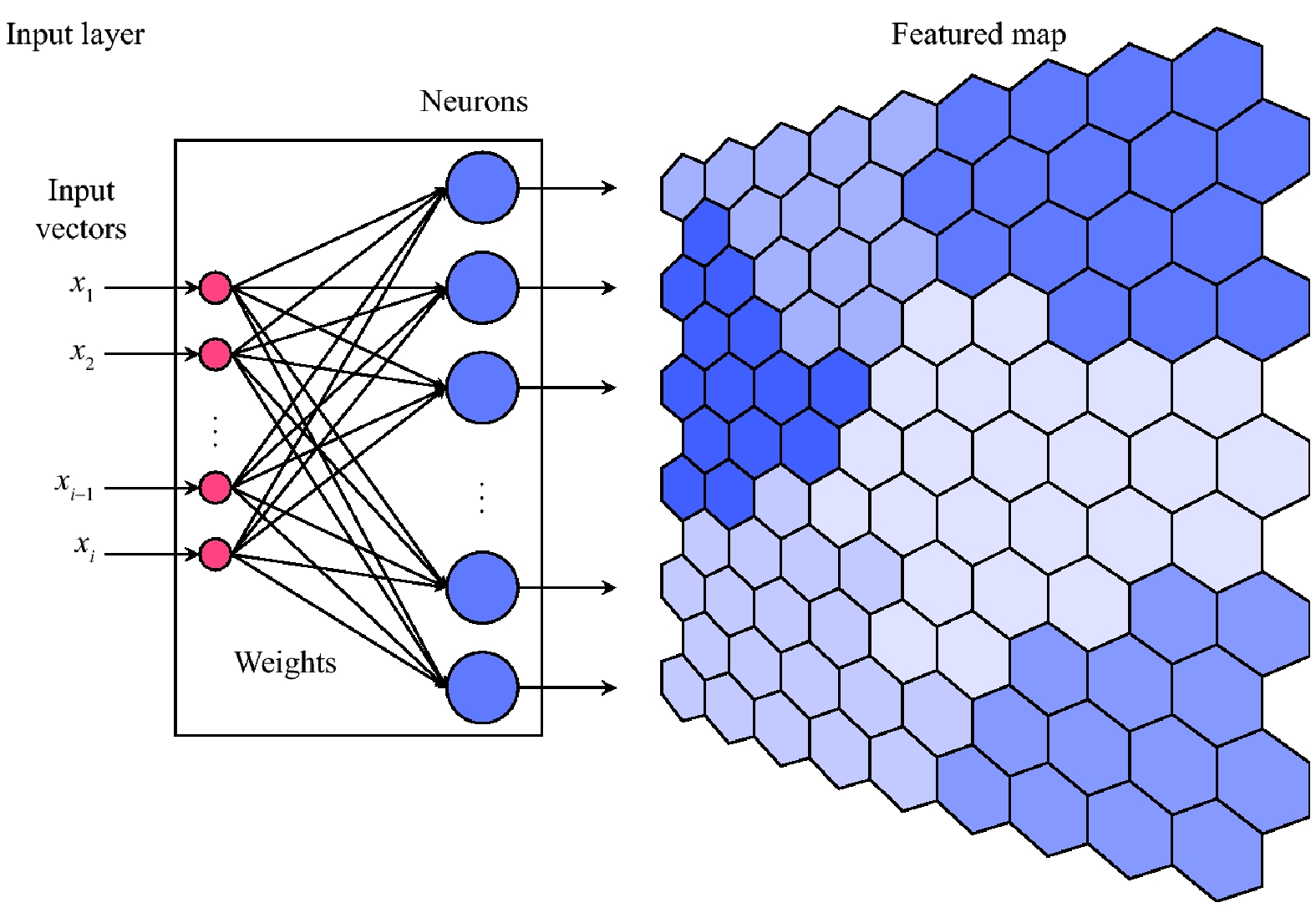
SOM的拓扑映射示意如图1所示。
图1左侧是SOM的计算过程,右侧是将SOM输出进行可视化的结果,右侧中的每个单元六边形对应代表左侧的一个神经元,从而得到由六边形单元组成的二维网格。在SOM的训练过程中,相似的输入向量被映射到特征图中的邻近区域,因此,可以根据输出的特征区域数(文中为不同颜色块数量(6个)),将其直接设置为K-Means的聚类数目,从而为K-Means聚类算法提供了一种自然和直观的数据预处理方法[7]。
1.3 算法复杂度分析
K-Means聚类算法的时间复杂度为O(k×n×t),其中,k是聚类中心的个数;n是样本数量;t是迭代次数。在实际应用中,为选出最优的k值,常需要执行多次K-Means聚类算法,每次都伴随对应轮廓系数的计算。轮廓系数计算的时间复杂度为O(n2),当需要多次计算以评估不同的k值时,总体耗时将会成倍增加。而SOM的训练只涉及每个输入向量与网络中所有神经元权重的比较,其复杂度可近似表示为O(d·m·i),其中,
d 是输入向量的维度;m是神经元的数量;i是迭代次数。尽管这一过程在理论上较为耗时,但在实际应用中通常会对SOM进行批量训练和并行计算,可有效降低实际运行时间。融合SOM与K-Means的聚类算法(简称:本文算法),是将SOM初步聚类后的区域个数作为K-Means的聚类中心初始值,因此,K-Means聚类算法仅需要执行一次,避免对多个不同k值的尝试及对应的轮廓系数计算,时间复杂度降为O(d·t),时间效率得到了极大提升。
2 聚类效果实证分析
本文通过分析借贷实证数据,提取用户的还款意愿和还款能力,实现用户信用画像的构建。其中,还款意愿涵盖用户的信用信息,包括信用评级、最近6个月的查询次数、在过去2年内逾期超过30天的次数等属性;而还款能力与用户的基本信息相关,包括年收入、资产负债比、房产拥有情况及工作年限等。
从实证数据构建标签、建立用户信用画像的主要步骤包括:对原始数据中所有特征进行筛选,从而获取与用户信用画像相关的目标标签;根据所选特征,通过聚类算法对特征进行划分,生成特征等级标签;通过特征等级标签建立用户信用画像。
2.1 特征选择方法
特征选择是机器学习中的一个关键步骤,可确保SOM的效率和有效性。过滤法是一种基于特征和目标变量之间的统计相关性进行特征选择的方法,效率较高;而嵌入法则是将特征选择与学习器训练过程相结合,在训练过程中自然地选择出重要特征,避免单独的特征选择步骤可能带来的信息损失[8]。
本文将过滤法和嵌入法相结合,根据特征相关性将用户特征划分成若干组,采取基于树结构的特征选择方法。在拟合决策树时,从根结点开始以纯净度指标及基尼指数为整体优化目标,记录各分割对整体优化目标的影响,从而计算得到最优分割。
2.2 数据处理
LendingClub是一个成立于2006年的美国在线借贷平台,为个人和企业提供贷款和投资机会[9]。本文使用该平台数据集loan data中2007—2015年间的信用贷款数据,共74个属性和超过88万条记录。数据集的部分特征说明,如表1所示。
表 1 数据集字段说明(部分)字段名称 字段含义 数据说明 loan_amnt 贷款金额 借款人的贷款金额 annual_inc 年收入 借款人的自报年收入 delinq_2yrs 逾期次数 过去2年内逾期30天以上的次数 open_acc 未结信用额度数量 借款人未结信用额度的数目 Grade 用户信用等级 按风险递增分级 Term 贷款期限 分36个月和60个月 tot_coll_amt 欠款金额 用户所有欠款账户所欠总金额 2.2.1 数据预处理
对原始loan data数据集进行预处理,该数据集包含
887379 行和74列。处理步骤和结果如下。(1) 缺失数据处理:通过统计分析发现,有21个特征的缺失比例超过50%。鉴于填充这些特征数据已无意义,可直接移除。此外,一些非数值型的字段如emp_title(职位)、desc(贷款需求)、next_pymnt_d(下次还款日期)等,由于缺乏样本之间的关联性,也不能通过常规方法填充,同样被移除。
(2) 异常值检查:通过对数据集进行可视化分析可知,除年收入外,其他列的差异较小,因此收入不均被视为正常现象,不考虑作为异常值处理。
(3) One-hot 编码处理:对数据集中非数值型特征进行one-hot编码,将分类值映射为数值型,便于数据分析和模型调用。
(4) 还款情况字段处理:还款情况分为正常还款、逾期还款和其他这3类。正常还款包括Fully Paid(结清)、Current(正常还款)、In Grace Period(宽限期)这3种状态,逾期还款包括Late(逾期16天~30天)、Late(逾期31天~120天)、Charged Off(坏账)、Default(违约)这4种状态,其他状态自动归类为其他。
2.2.2 特征分组
在去除缺失值、异常值及与用户信用无关的特征以后,共剩余28个特征。根据特征所代表的借款人财务和信用的不同状况,将特征分为4个组别[10],各组包含特征如表2所示。
表 2 特征分组情况组别 特征 特征字段 第1组 贷款的基本属性和借款人的还款情况 recoveries: 回收金额 total_rec_int: 总利息 revol_util: 循环利用率 emp_title: 借款人职位 application_type: 申请类型 term_range: 贷款期限范围 acc_now_delinq: 逾期账户数 第2组 借款人的信用历史和财务稳定性 dti: 债务收入比 annual_inc: 年收入 total_pymnt: 总还款额 grade_range: 信用等级 emp_length_range: 工作年限 delinq_2yrs: 过去2年逾期次数 home_ownership_range: 住房所有权 第3组 借款人的信用状况和贷款条件 int_rate: 贷款利率 policy_code: 政策代码 addr_state: 地址所在州 tot_coll_amt: 总欠款金额 open_acc: 未结账户数量 revol_bal: 循环信用余额 pymnt_plan_range: 还款计划 第4组 贷款的特征、借款人的概况和还款计划 pub_rec: 公共记录 loan_amnt: 贷款金额 emp_title: 借款人的职位 installment: 分期付款额 tot_cur_bal: 目前总余额 term_range: 贷款期限范围 verification_status_range: 收入范围 2.2.3 特征组别预测性能评估
分别对上述4组特征进行基于决策树的分类预测,结果如表3所示。众多评估指标中,本文采用了2个关键的指标:准确率(Accuracy)和曲线下面积(AUC,Area Under the Curve)。准确率是一个直观的性能度量指标,它表示模型正确预测的样本数占总样本数的比例;AUC是一个衡量模型区分不同类别样本能力的指标,AUC值的范围为0~1,其中,1表示完美的分类器,0.5表示随机猜测,其值越接近1表示模型的分类性能越好。
表 3 特征分类预测结果组别 准确率 AUC 第1组 94.70% 0.6732 第2组 98.10% 0.8324 第3组 92.42% 0.5082 第4组 92.71% 0.5235 由表3可知,第2组特征(借款人的信用历史和财务稳定性)对用户信用方面的刻画是最准确的。针对信用画像目标,考虑将第2组特征分成2种类别:第1类为信用历史,反映用户还款意愿,涵盖信用评级、过去2年的逾期次数、未偿还本金等因素;而第2类为财务稳定性,反映用户还款能力,包括年收入、资产负债比率、工作年数、房产所有权等因素。采用本文算法为用户还款意愿和还款能力的特征进行聚类,得到特征等级标签。
2.3 还款意愿和还款能力聚类
2.3.1 还款意愿聚类
针对用户还款意愿,先通过SOM对数据进行分析,计算与用户还款意愿相关的特征,再进行可视化处理,得到还款意愿特征聚类图,如图2所示。
图2中有3种不同颜色的邻接区域,可考虑将还款意愿聚类成3类,根据每类数据从高到低,将还款意愿划分成高、中、低3个等级。
为验证本文算法可准确获得与传统K-means算法一样的聚类结果,使用K-means对数据进行聚类,并通过计算轮廓系数评估聚类质量[11],较高的轮廓系数值表示在相同条件下取得更好的聚类结果。针对还款意愿,采用K-Means聚类算法进行聚类,并计算轮廓系数,如表4所示。
表 4 针对还款意愿的聚类数目及轮廓系数聚类数目 轮廓系数 2 0.4834 3 0.5256 4 0.4962 5 0.5183 由表4可知,聚类数目为3时采用K-Means聚类算法的效果最佳。而图2中针对还款意愿采用SOM的聚类图中不同颜色块个数也为3,验证了用SOM进行初始聚类的准确性。
2.3.2 还款能力聚类
同理,针对用户还款能力,利用SOM对与用户还款能力相关的特征数据进行降维计算,再进行可视化处理,得到还款能力特征聚类图,如图3所示。
图3中有4种不同颜色的邻接区域,可考虑还款能力聚类成4类。再根据色块所占面积大小,将还款能力分为高、良、中、差4个等级。针对还款能力,采用K-Means聚类算法进行聚类,并计算轮廓系数,如表5所示。
表 5 针对还款能力的聚类数目及轮廓系数聚类数目 轮廓系数 2 0.4250 3 0.3732 4 0.4754 5 0.4253 由表5可知,聚类数目为4时,K-Means聚类算法的效果最佳,而图3中SOM聚类的不同颜色块个数也为4,验证了用SOM进行初始聚类的准确性。
2.3.3 用户信用画像生成
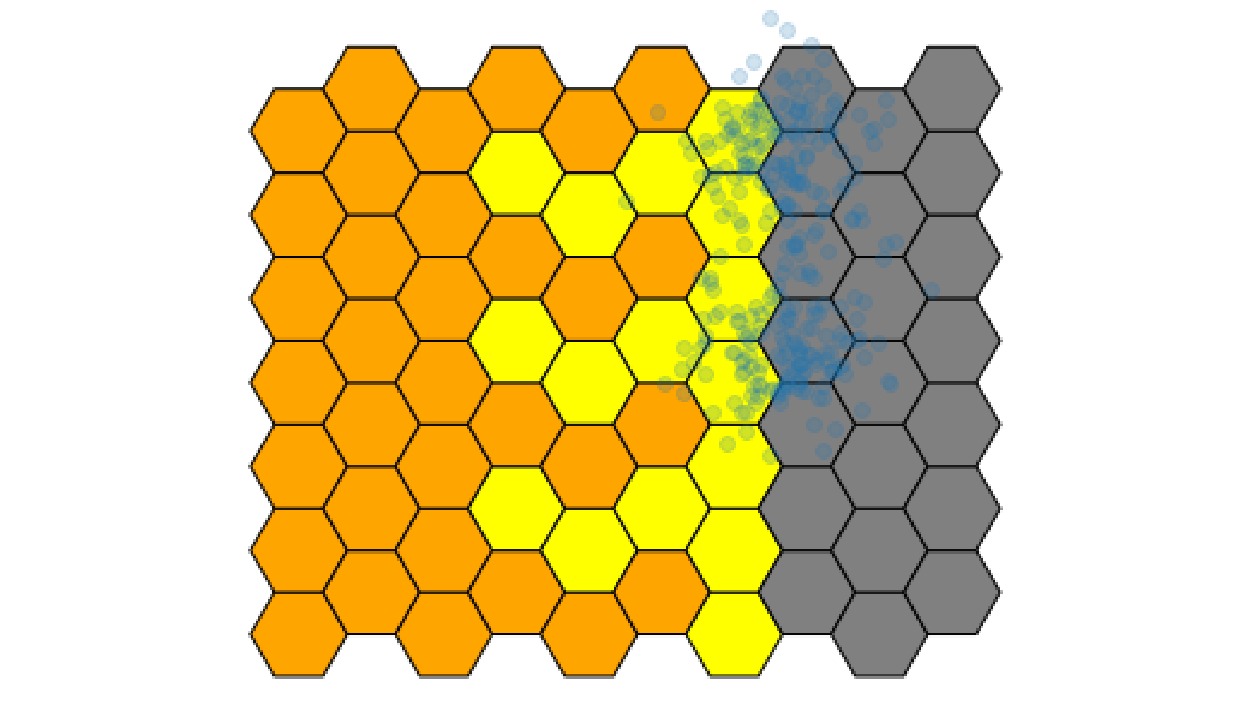
将上述方法和结果应用于实际用户信用评价中,基于信用评价常用的“5C理论”(品质、条件、资本、能力、抵押)[10],针对贷款数据[9],对应违约概率、信用等级、贷款额度、还款能力、还款意愿这5个标签,部分的用户信用标签如表6所示,其对应的用户信用画像如图4所示。其中,贷款额度和信用等级是贷款机构根据自身数据衡量用户历史信用的标签;而还款意愿和还款能力是通过上节聚类方法衡量用户未来信用的标签;违约概率是贷款机构对上述4个信用标签(贷款额度、信用等级、还款意愿、还款能力)加权计算、综合评估后给出的标签[9]。
表 6 用户信用标签(部分)用户ID 违约概率 贷款额度 信用等级 还款意愿 还款能力 44521 中 中 高 中 良 23423 高 中 低 低 高 678565 低 高 中 高 中 对图4中ID为678565的用户进行分析,尽管贷款机构衡量其贷款额度高、信用等级中等,但本文算法得出其还款能力中等、还款意愿高,从而得出违约概率较低的综合评估结果。可见本文算法对还款能力和还款意愿的聚类结果能够更精确地量化用户的信用等级。
3 结束语
本文提出融合SOM神经网络与K-Means聚类算法的用户信用画像分析,实现不同信用用户类别的划分。通过分析各个类别中用户的属性,在获得精细化的用户信用画像同时,有效降低算法的时间复杂度,对金融机构在用户信用评级、实时风险控制、市场营销策略制定、个性化服务提供等方面提供有力支持。本文算法在标签体系和特征维度上仍有完善的空间,未来,可以考虑通过迭代来更新标签的权重,形成全面评估用户信用风险的评分系统,进一步优化用户信用画像的特征提取,增强其在实际风险控制中的有效性和准确性。
-
表 1 数据集字段说明(部分)
字段名称 字段含义 数据说明 loan_amnt 贷款金额 借款人的贷款金额 annual_inc 年收入 借款人的自报年收入 delinq_2yrs 逾期次数 过去2年内逾期30天以上的次数 open_acc 未结信用额度数量 借款人未结信用额度的数目 Grade 用户信用等级 按风险递增分级 Term 贷款期限 分36个月和60个月 tot_coll_amt 欠款金额 用户所有欠款账户所欠总金额 表 2 特征分组情况
组别 特征 特征字段 第1组 贷款的基本属性和借款人的还款情况 recoveries: 回收金额 total_rec_int: 总利息 revol_util: 循环利用率 emp_title: 借款人职位 application_type: 申请类型 term_range: 贷款期限范围 acc_now_delinq: 逾期账户数 第2组 借款人的信用历史和财务稳定性 dti: 债务收入比 annual_inc: 年收入 total_pymnt: 总还款额 grade_range: 信用等级 emp_length_range: 工作年限 delinq_2yrs: 过去2年逾期次数 home_ownership_range: 住房所有权 第3组 借款人的信用状况和贷款条件 int_rate: 贷款利率 policy_code: 政策代码 addr_state: 地址所在州 tot_coll_amt: 总欠款金额 open_acc: 未结账户数量 revol_bal: 循环信用余额 pymnt_plan_range: 还款计划 第4组 贷款的特征、借款人的概况和还款计划 pub_rec: 公共记录 loan_amnt: 贷款金额 emp_title: 借款人的职位 installment: 分期付款额 tot_cur_bal: 目前总余额 term_range: 贷款期限范围 verification_status_range: 收入范围 表 3 特征分类预测结果
组别 准确率 AUC 第1组 94.70% 0.6732 第2组 98.10% 0.8324 第3组 92.42% 0.5082 第4组 92.71% 0.5235 表 4 针对还款意愿的聚类数目及轮廓系数
聚类数目 轮廓系数 2 0.4834 3 0.5256 4 0.4962 5 0.5183 表 5 针对还款能力的聚类数目及轮廓系数
聚类数目 轮廓系数 2 0.4250 3 0.3732 4 0.4754 5 0.4253 表 6 用户信用标签(部分)
用户ID 违约概率 贷款额度 信用等级 还款意愿 还款能力 44521 中 中 高 中 良 23423 高 中 低 低 高 678565 低 高 中 高 中 -
[1] 张 华,王 丽,李 强. 金融行业中用户画像的构建及其在信贷风险评估中的应用研究[J]. 金融科技时代,2020,7(2):45-54. [2] 李 明,周 健,张 伟. 基于大数据的用户画像在个性化金融服务中的应用[J]. 经济管理,2021,39(4):112-120. [3] 蔡晓妍,戴冠中,杨黎斌. 谱聚类算法综述[J]. 计算机科学,2008,35(7):14-18. DOI: 10.3969/j.issn.1002-137X.2008.07.004 [4] 邓 祥,俞 璐. 深度聚类算法综述[J]. 通信技术,2021,54(8):1807-1814. DOI: 10.3969/j.issn.1002-0802.2021.08.001 [5] 周广利. 大数据背景下商业银行信贷安全管理策略研究——评《风控:大数据时代下的信贷风险管理和实践》[J]. 中国安全科学学报,2021,31(2):187-188. [6] 张秉楠,李德玉. 融合协同过滤的自组织神经网络多样化产品推荐[J/OL]. 山西大学学报(自然科学版):1-10[2024-06-21]. https://doi.org/10.13451/j.sxu.ns.2023068. [7] 郭伟业,赵晓丹,庞英智,等. 数据挖掘中SOM神经网络的聚类方法研究[J]. 情报科学,2009,27(6):874-876,893. [8] 姚 旭,王晓丹,张玉玺,等. 特征选择方法综述[J]. 控制与决策,2012,27(2):161-166,192. [9] 普雪飞. P2P网贷信用风险量化评估研究——以Lending Club平台为鉴[D]. 成都:电子科技大学,2020. [10] 薛 琦,罗鄂湘. 基于机器学习的银行个人信用风险评估研究[J]. 建模与仿真,2023,12(4):3747-3755. [11] 杨俊闯,赵 超. K-Means聚类算法研究综述[J]. 计算机工程与应用,2019,55(23):7-14,63. -
期刊类型引用(3)
1. 沈希臻,陈儒敏. 基于改进YOLOv3的病虫害识别算法研究. 智能计算机与应用. 2025(02): 85-90 .  百度学术
百度学术
2. 刘励耘,许孝梅. 基于图注意力网络与聚类的用户画像研究. 云南电力技术. 2025(01): 68-75+85 .  百度学术
百度学术
3. 曾亚,孙亚琴. 基于SOM神经网络的网络舆情信息分类方法研究. 长江信息通信. 2025(03): 153-155 .  百度学术
百度学术
其他类型引用(0)




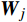
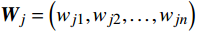
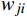
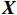
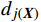
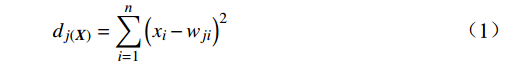


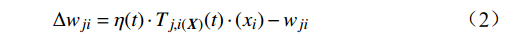

 下载:
下载: