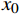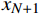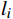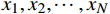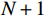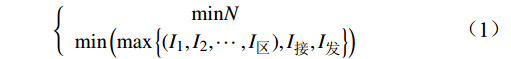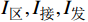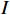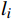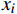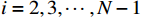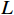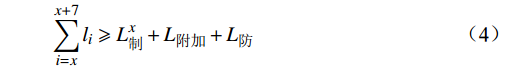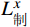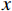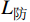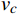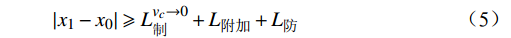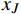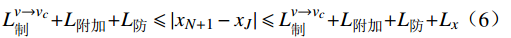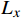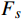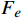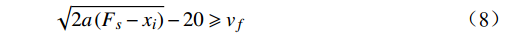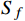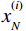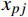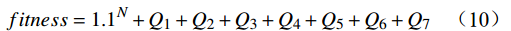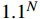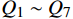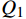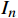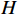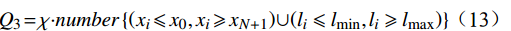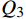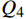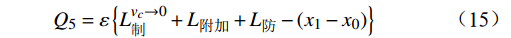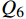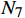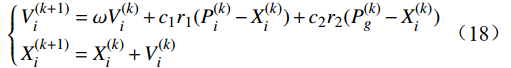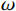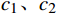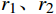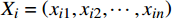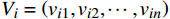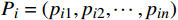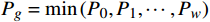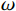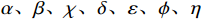Optimization of high-speed railway block section based on multi-objective strategy
-
摘要:
为探究适用于CTCS-3级列车运行控制系统的高速铁路闭塞分区划分方法,分析影响闭塞分区划分的因素,在确保列车运行安全的前提下,构建多目标策略下的CTCS-3级高速铁路闭塞分区划分模型,采用粒子群算法对模型求解,并优化了算法中的适应度函数。通过在京沪(北京—上海)高速铁路滕州东—枣庄区间的实例验证表明,文章提出的优化方法能够有效缩短行车间隔,对高速铁路闭塞分区的设计具有实际意义。
Abstract:To explore the high-speed railway block section partitioning method applicable to the CTCS-3 level train operation control system, this paper analyzed the factors affecting block section partitioning, constructed a multi-objective strategy based CTCS-3 level high-speed railway block section partitioning model, on the premise of ensuring the safety of train operation, used particle swarm optimization algorithm to solve the model, and optimized the fitness function in the algorithm. The case study on the Tengzhou East - Zaozhuang section of the Beijing Shanghai high-speed railway shows that the optimization method proposed in this paper can effectively shorten the train running interval and has practical significance for the design of high-speed railway block section.
-
我国高速铁路采用能使列车在区间安全运行的自动闭塞方式,根据列车运行速度,区间的多个闭塞分区构成列车安全追踪运行间隔,闭塞分区的长度直接影响列车追踪间隔的精度[1]。若闭塞分区设置过长,虽能保证列车安全制动和舒适驾驶的需要,但会造成不必要的列车间隔距离浪费;若闭塞分区设置过短,虽能发挥线路的运输效率,但存在一定的安全风险和额外设备投资。因此,在进行闭塞分区设计时,须在确保列车运行安全的前提下满足运输效率、减少设备投资的要求。
目前,国内外许多学者对闭塞分区进行了相关研究。Gill D.C等人[2]面向城市轨道交通,采用多目标结合启发式的梯度算法求解闭塞分区的优化问题;Chang C.S等人[3]使用差分进化算法和遗传算法,研究城市轨道交通区间通过信号机的位置划分;Ke B.R等人[4]使用最大−最小蚁群系统,建立了以节能为目标的地铁线路区间固定闭塞分区布置方案;刘海东等人[5]将差分进化算法进行改进,并用于求解高速铁路闭塞分区的设计问题;王丹彤等人[6]通过整体分布优化算法,对高速铁路进站前的若干个闭塞分区进行优化,将列车区间和进站间隔进行整体考虑;还有一些学者考虑效率或经济策略,构建铁路区间闭塞分区分布模型,并利用遗传算法、差分进化算法、粒子群算法等对其进行求解[7-9]。
国外的相关研究多集中于城市轨道交通闭塞分区的布置,国内学者虽然已将智能寻优算法应用于求解干线普速铁路和200 km/h客运专线的闭塞分区布置问题上,但针对适用于CTCS-3级列车运行控制系统(简称:列控系统)要求的铁路闭塞分区研究相对较少,且得到的结果多与实际线路差距较大,其原因是布置方案并未综合考虑闭塞分区划分的实际需求,不能很好地应用于实际线路设计[10-12]。
本文基于CTCS-3级列控系统控车原理,综合考虑闭塞分区划分目标及影响因素,构建CTCS-3级列控系统下的高速铁路闭塞分区划分模型,并使用粒子群算法进行模型求解。
1 闭塞分区划分影响因素
高速铁路闭塞分区的设计应全面考虑影响闭塞分区长度及分界点位置的因素,如采用的列控系统、闭塞方式、线路条件、列车类型、安全制动距离、行车间隔和分相区位置及长度等。
1.1 列车安全制动距离
实现列车在区间安全追踪运行是闭塞分区设计划分的首要目标。列车安全制动距离是由列车有效制动距离、安全余量及司机和列控系统反应时间内的列车走行距离确定的。在进行闭塞分区划分时,应按码序显示条件进行列车安全制动距离检验。
1.2 列车种类
列车运行速度及性能决定了列车制动距离,因此,闭塞分区的设置应充分考虑在该线路上运行的列车参数。
1.3 区间信号显示制式
信号系统采取的闭塞方式及显示模式直接决定了两列车间能够间隔的最大闭塞分区数目及列车间隔距离。
1.4 列车追踪间隔及通过能力
列车追踪间隔、线路通过能力的要求是闭塞分区设置需满足的运营条件,也是闭塞分区设计的制约点。本文基于采用目标距离一次制动模式的CTCS-3级列控系统,在固定自动闭塞制式下,参考相关资料[13],计算列车运行间隔时间。
1.5 线路条件
线路条件是设计区间信号闭塞分区的基础数据,具体体现在计算列车安全制动距离时坡度等参数对列车制动减速度的影响。
1.6 分相区的位置及长度
分相区是一个接触网无牵引的区域,列车在区间需要依靠惯性惰行经过分相区,闭塞分区的设置应能保证列车安全通过分相区。
2 多目标策略下的闭塞分区划分模型
闭塞分区的划分应在满足各影响因素的条件下,主要考虑安全、效率、经济等3个方面的优化目标。三者相互约束,其中,安全是铁路运输的前提,在此前提下,建立高速铁路闭塞分区划分模型,如图1所示。
图中,甲、乙为2个相邻的车站;
${x_0}$ 为甲站反向进站信号机的位置;${x_{N + 1}}$ 为乙站进站信号机的位置;${l_i}$ 为每个闭塞分区的长度;$ x_1,x_2,\cdots ,x_N $ 为闭塞分区分界点的位置;区间共$N + 1$ 个闭塞分区。2.1 目标函数
在满足行车安全和闭塞分区各约束条件的目标下,构建以闭塞分区数目最少和列车运行间隔最小的优化目标函数,公式为
$$ \left\{\begin{array}{c}\mathrm{min}N\\ \mathrm{min}\left(\mathrm{max}\left\{({I}_{1},{I}_{2},\cdots ,{I}_{区}),{I}_{接},{I}_{发}\right\}\right)\end{array}\right. $$ (1) 式(1)中,
$ {I}_{区},{I}_{接},{I}_{发} $ 分别为列车在区间运行、车站接车和发车的间隔时间。列车运行间隔时间$I$ 为各运行场景下行车间隔的最大值。2.2 约束条件
根据影响闭塞分区设计的因素,建立闭塞分区划分模型的约束条件。
(1)区间信号分界条件
区间的所有分界点必须位于信号规定范围内,表示为
$$ \left\{ \begin{gathered} {x_0} \leqslant {x_i} \leqslant {x_{N + 1}} \\ {x_{i - 1}} \leqslant {x_i} \\ \end{gathered} \right. $$ (2) (2)闭塞分区长度条件
CTCS-3级列控系统区间闭塞分区通常设置为2000 m左右,除列车进站接近区段和列车出站第一离去区段外,闭塞分区长度一般不大于3000 m,不小于1500 m[14],表示为
$$ \left\{ \begin{gathered} {l_{\min }} \leqslant {l_i} \leqslant {l_{\max }} \\ \frac{L}{{{l_{\max }}}} \leqslant N \leqslant \frac{L}{{{l_{\min }}}} \\ \end{gathered} \right. $$ (3) 式(3)中,
$ {l_i} $ 为以${x_i}$ 信号点为防护分界闭塞分区的长度,$ i = 2,3, \cdots ,N - 1 $ ;$ L $ 为区间总长度。(3)列车安全制动距离
CTCS-3级列控系统区间满足安全追踪间隔运行可分配的码序最大数量为7。信号系统追踪码序匹配相应闭塞分区的长度之和须满足安全制动距离,表示为
$$ {\displaystyle \sum _{i=x}^{x+7}{l}_{i}\geqslant{L}_{制}^{x}+{L}_{附加}}+{L}_{防} $$ (4) 式(4)中,
$ {L}_{制}^{x} $ 为列车在$x$ 位置处以最高运行速度开始制动的最大常用制动距离;$ {L}_{附加} $ 为列车在制动附加时间的运行距离;$ {L}_{防} $ 为安全防护距离。(4)出站一离去区段
一离去区段制约列车发车间隔,一离去区段位置x1至相邻信号点
${x_0}$ (反向进站信号机)的距离,须满足以出站最高限速$ {v_c} $ 运行至停车的制动距离,表示为$$ \left|{x}_{1}-{x}_{0}\right|\geqslant{L}_{制}^{{v}_{c}\to 0}+{L}_{附加}+{L}_{防} $$ (5) (5)进站接近区段
进站接近区段应设置相对较短,尽量缩短进站间隔时间以均衡车站和区间的行车间隔。进行闭塞分区布置时,接近区段起点信号分界
$ {x_J} $ 应满足$$ {L}_{制}^{v\to {v}_{c}} + {L}_{附加} + {L}_{防}\leqslant \left|{x}_{N+1}-{x}_{J}\right|\leqslant {L}_{制}^{v\to {v}_{c}} + {L}_{附加} + {L}_{防} + {L}_{x} $$ (6) 式(6)中,
$ {L_x} $ 为接近锁闭区段起始闭塞分区的长度。(6)分相区约束条件
闭塞分区分界点不可设在分相区内,表示为
$$ {x_i} \notin \left[ {{F_s},{F_e}} \right] $$ (7) 式(7)中,
$ {F_s} $ 为分相区断电标位置;$ {F_e} $ 为分相区合电标位置。分相区后的信号分界点须保证列车在该位置重新启动后安全通过分相区,表示为
$$ \sqrt {2a\left( {{F_s} - {x_i}} \right)} - 20 \geqslant {v_f} $$ (8) 分相区前方的闭塞分区分界点应满足以下条件,表示为
$$ {x_i} - {F_e} \geqslant {S_f} $$ (9) 式(9)中,
${v_f}$ 为列车安全过分相区的最小限速,取值30 km/h;${S_f}$ 为分相终点至前方信号分界点的最小长度,取值300 m。3 模型求解
本文选择在多目标优化问题求解方面已应用成熟的粒子群算法对本文建立的模型进行求解。
3.1 算法实现流程
粒子群算法求解流程如图2所示。
(1)随机生成初始化粒子的位置和速度;
(2)计算初始种群的适应度值,根据适应度值寻找初始种群中的最优解,为个体最优值;
(3)更新粒子的速度和位置,计算新粒子的适应度值,并与历史局部最优解进行适应度值比较,若优于历史,则进行更新;
(4)判断是否达到迭代终止条件,若达到终止条件,则输出最终的最优结果及算法迭代次数。
3.2 初始种群生成
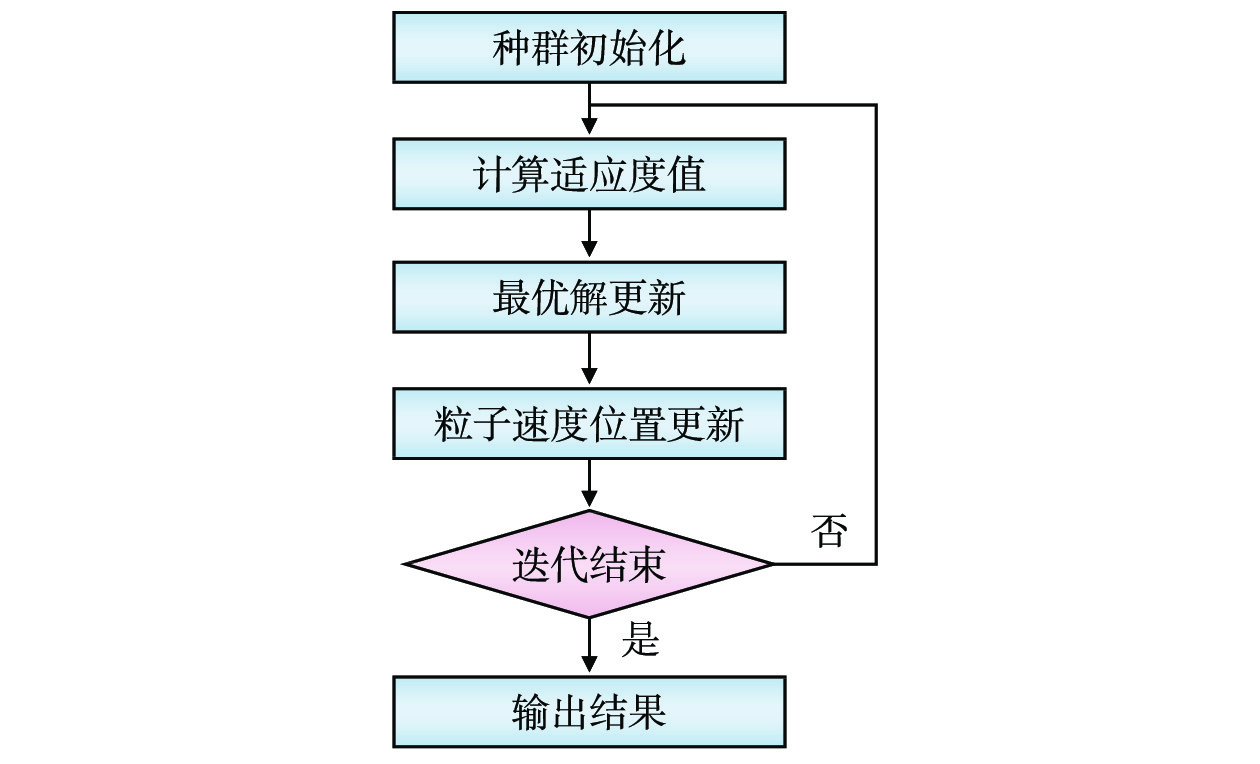
用长度为N的数组
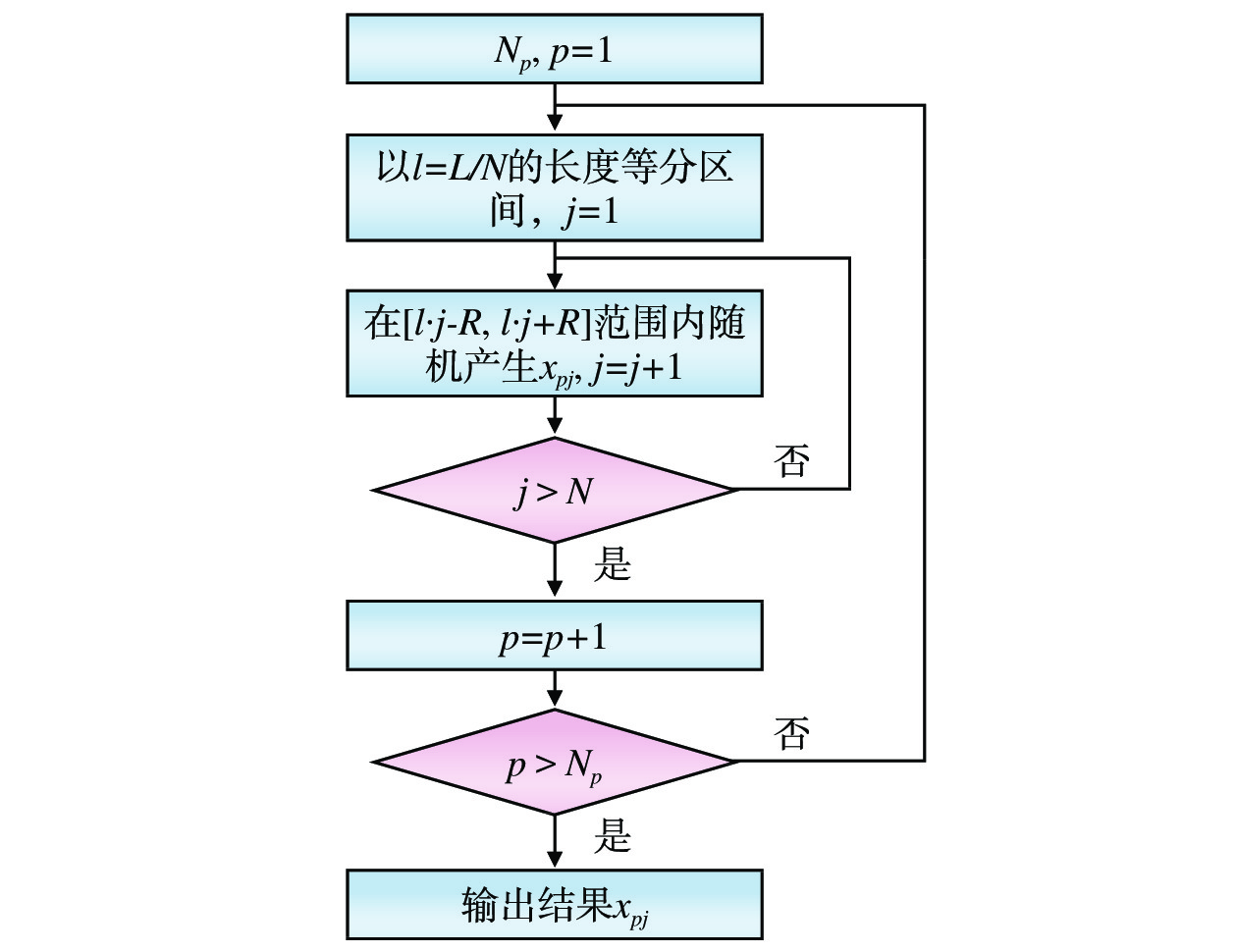
$ {x^{(i)}} = \left( {x_{_1}^{^{(i)}},x_{_2}^{^{(i)}}, \cdots ,x_{_N}^{^{(i)}}} \right) $ 表示一种迭代至第i代的模型求解结果,第N个分界点的位置为数组中的$ x_{_N}^{^{(i)}} $ 。为了加快粒子收敛速度得到最优结果,需要生成一个较优初始解,便于后续进行准确有效的搜索。算法初始种群生成的流程如图3所示。
图3中,NP为初始种群的数量,从第1个种群p=1开始初始化;N为初始种群数组的长度,即划分的闭塞分区分界点数目,是在由式(3)确定的取值范围内随机产生的整数;
$ {x_{pj}} $ 为粒子位置,表示第p个种群内的第j个闭塞分区分界点;R为粒子的搜索速度,取100~200范围内的随机数。3.3 适应度函数构建
求解时将约束条件通过惩罚函数的引入算法,根据目标函数及相应的约束条件构建适应度函数,适应度函数值越小表示划分结果越好,公式为
$$ fitness = {1.1^N} + {Q_1} + {Q_2} + {Q_3} + {Q_4} + {Q_5} + {Q_6} + {Q_7} $$ (10) 式(10)中,
$ {1.1^N} $ 表示划分的闭塞分区越少,适应度值越小。$ {Q_1}\sim{Q_7} $ 为惩罚函数,均为2.2节约束条件的具体体现,公式为$$ {Q_1} = \left\{ {\begin{array}{*{20}{c}} {\alpha\displaystyle \sum {\left( {{I_n}{{ - }}H} \right)} }&{{I_n} \geqslant H} \\ 0&{{I_n} \leqslant H} \end{array}} \right. $$ (11) 式(11)中,
$ {Q_1} $ 为行车追踪时间约束的惩罚函数;$ {I_n} $ 为当前划分方案下的列车间隔时间;$ H $ 为规定的行车间隔。$$ {Q_2} = \beta \sum\limits_{i = 1}^{N - 1} {\left| {{l_i} - {l_{\min }}} \right|} $$ (12) 式(12)中,
$ {Q_2} $ 为除去进站接近区段和一离去区段外,闭塞分区最小长度与每个闭塞分区的长度的差值之和。$$ Q_3 = \chi \cdot number\left\{\left(x_i \leqslant x_0,x_i \geqslant x_{N+1}\right) \cup \left(l_i\leqslant l_{\min},l_i\geqslant l_{\max}\right)\right\} $$ (13) 式(13)中,
$ {Q_3} $ 为闭塞分区长度范围和超出区间分界范围约束的惩罚函数。$$ {Q}_{4}=\delta {\displaystyle \sum _{j=1}^{{N}_{4}}\left({L}_{制}^{x}+{L}_{附加}+{L}_{防}-{\displaystyle \sum _{i=x}^{x+7}{l}_{i}}\right)} $$ (14) 式(14)中,
$ {Q_4} $ 为不满足在CTCS-3级列控系统码序间隔下安全制动距离的闭塞分区,${N_4}$ 为闭塞分区的个数。$$ {Q}_{5}=\varepsilon \left\{{L}_{制}^{{v}_{c}\to 0}+{L}_{附加}+{L}_{防}-({x}_{1}-{x}_{0})\right\} $$ (15) 式(15)中,
$ {Q_5} $ 为一离去区段信号点的限制约束对应的惩罚函数。$$ {Q_6} = \varphi \left| {{x_c} - {x_J}} \right| $$ (16) 式(16)中,
$ {Q_6} $ 为进站接近区段信号点约束对应的惩罚函数;$ {x_c} $ 为接近区段分界的限制位置。$$ {Q_7} = \eta {N_7} $$ (17) 式(17)中,
$ {Q_7} $ 为分相区约束的惩罚函数,$ {N_7} $ 为个数。$ \alpha 、\beta 、\chi 、\delta 、\varepsilon 、\phi 、\eta $ 为惩罚因子,根据模型设计的目标函数和约束重要度取值。3.4 种群更新
种群更新的速度和位置如下:
$$ \left\{ \begin{gathered} V_i^{(k + 1)} = \omega V_i^{(k)} + {c_1}{r_1}(P_i^{(k)} - X_i^{(k)}) + {c_2}{r_2}(P_g^{(k)} - X_i^{(k)}) \\ X_i^{(k + 1)} = X_i^{(k)} + V_i^{(k)} \\ \end{gathered} \right. $$ (18) 式(18)中,
$ \omega $ 为惯性权重;$ {c}_{1}、{c}_{2} $ 为常数;k为迭代次数;$ {r}_{1}、{r}_{2} $ 为范围在0~1之间的随机数。$ {X_i} = \left( {{x_{i1}},{x_{i2}}, \cdots ,{x_{in}}} \right) $ 为粒子的位置;$ {V_i} = \left( {{v_{i1}},{v_{i2}}, \cdots ,{v_{in}}} \right) $ 为粒子的搜索速度;$ {P_i} = \left( {{p_{i1}},{p_{i2}}, \cdots ,{p_{in}}} \right) $ 为适应度值最优时种群内粒子的位置。对于求解多目标最小化问题,若粒子总数为w,求解的全局最优值Pg为群体中所有粒子的最优位置,
$ {P_g} = \min \left( {{P_0},{P_1}, \cdots ,{P_w}} \right) $ 。4 算例验证
本文选取CTCS-3级列控系统在京沪(北京—上海)高速铁路滕州东—枣庄下行区间的线路数据,使用多目标策略下的粒子群算法对闭塞分区划分模型进行求解。
4.1 计算数据设置
待划分的滕州东站—枣庄区间线路数据如表1所示,区间总长34279 m。
表 1 区间基本信息站名 出站信号机坐标 进站信号机坐标 反向进站
信号机坐标滕州东 K592+389 — K593+005 枣庄 K628+610 K627+284 — 区间包含电分相区的起止点里程信息如表2所示。
表 2 区间分相区信息序号 起点里程 终点里程 长度 1 K610+187 K610+684 497 m 选取CRH3型动车组制动参数计算列车安全制动距离,如表3所示。
表 3 CRH3型动车组相关参数速度v/km·h-1 制动减速度/m·s-2 350~210 $ - 0.004\;3v + 0.710\;5$ 210~172 $ - 0.002\;1v + 1.061\;2 $ 172~160 $ - 0.025v + 5 $ 160以下 1 列车运行间隔时间计算相关参数根据文献[15]取值。
4.2 算法参数设置
利用MATLAB工具根据本文第3章描述的算法求解步骤编程求解,求解参数设置如下:初始种群设为30个,
$ \omega $ 取0.7,$ {c_1}{\text{ = }}{c_2} $ 取1.49,迭代次数取200。在寻求最优结果过程中,适应度函数中各惩罚因子的取值可根据适应度函数计算结果和各约束条件的重要度进行调整,以便求得更满足优化目标的结果,本文求解得到的最终结果中,惩罚因子$ \alpha 、\beta 、\chi 、\delta 、\varepsilon 、\phi 、\eta $ 取值依次为10、20、10、15、20、10、10。4.3 结果分析
使用粒子群算法对滕州东—枣庄区间闭塞分区划分结果如表4所示。
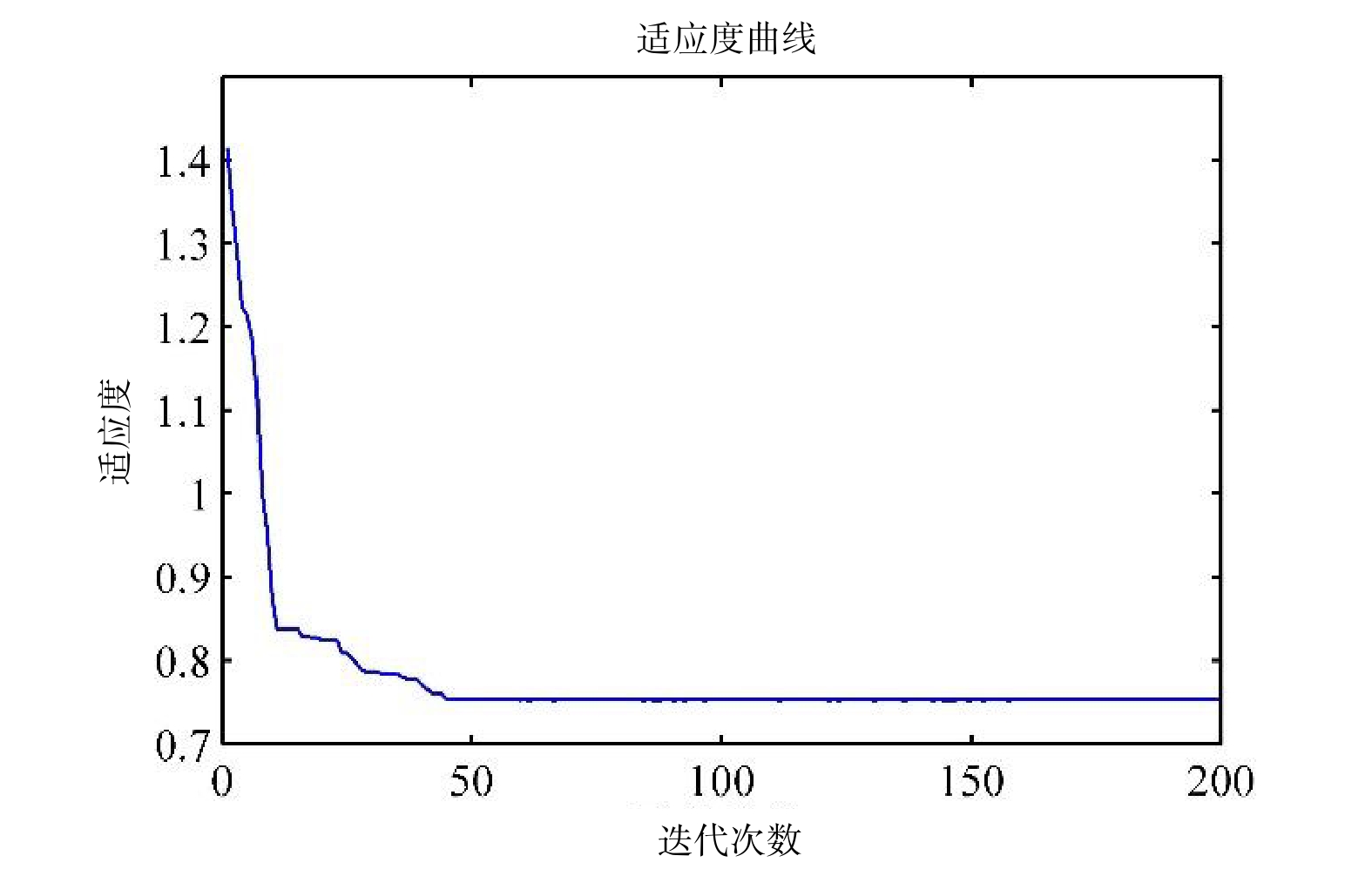
表 4 闭塞分区划分结果序号 分界点 闭塞分区/m 序号 分界点 闭塞分区/m 1 661.0 660.98 11 18191.0 1690.05 2 3464.7 1580.92 12 19881.0 1691.36 3 5045.7 1686.92 13 21572.4 1556.52 4 6732.6 1505.85 14 23128.9 1707.04 5 8238.4 1777.25 15 24835.9 1728.34 6 10015.7 1536.57 16 26564.3 1597.57 7 11552.2 1629.14 17 28161.8 1648.94 8 13181.4 1650.35 18 29810.8 1566.58 9 14831.7 1673.98 19 31377.4 1450.82 10 16505.7 1685.24 20 32828.2 1450.82 图4为闭塞分区划分算法的适应度函数变化曲线,算法最终趋于稳定,由图可知当迭代次数为46时,得到当前划分方案下的最优结果。
计算该结果下的行车间隔时间,并与实际线路进行对比,结果如表5所示。
表 5 划分结果对比分界点
个数区间
间隔/s进站
间隔/s出站
间隔/s运行间隔/s 实际线路 18 132.1 261.7 161.3 261.7 划分结果 20 130.1 251.9 147.9 251.9 结果表明,通过本文提出的基于粒子群算法的高速铁路闭塞分区优化模型得到的划分结果比实际线路增加2个闭塞分区,列车运行间隔时间缩短9.8 s。闭塞分区的设置结果与实际线路较为接近,是均衡考虑了列车运行间隔时间和闭塞分区数目的结果,更好地贴近闭塞分区划分设计的实际需求。
5 结束语
本文以分析影响高速铁路区间闭塞分区长度和位置的因素为基础,从闭塞分区布置设计的实际需求出发,综合考虑闭塞分区划分的效率和经济目标,建立基于CTCS-3级列控系统的高速铁路闭塞分区优化模型,并将闭塞分区的设置问题转换为有约束条件的优化问题,最后使用多目标粒子群算法以京沪高速铁路滕州东—枣庄区间为例,求解得到满足闭塞分区划分目标和贴近实际线路设置的结果。该优化模型很好地表达了高速铁路闭塞分区的设计需求,对高速铁路闭塞分区的优化设计具有实际意义。
-
表 1 区间基本信息
站名 出站信号机坐标 进站信号机坐标 反向进站
信号机坐标滕州东 K592+389 — K593+005 枣庄 K628+610 K627+284 — 表 2 区间分相区信息
序号 起点里程 终点里程 长度 1 K610+187 K610+684 497 m 表 3 CRH3型动车组相关参数
速度v/km·h-1 制动减速度/m·s-2 350~210 $ - 0.004\;3v + 0.710\;5$ 210~172 $ - 0.002\;1v + 1.061\;2 $ 172~160 $ - 0.025v + 5 $ 160以下 1 表 4 闭塞分区划分结果
序号 分界点 闭塞分区/m 序号 分界点 闭塞分区/m 1 661.0 660.98 11 18191.0 1690.05 2 3464.7 1580.92 12 19881.0 1691.36 3 5045.7 1686.92 13 21572.4 1556.52 4 6732.6 1505.85 14 23128.9 1707.04 5 8238.4 1777.25 15 24835.9 1728.34 6 10015.7 1536.57 16 26564.3 1597.57 7 11552.2 1629.14 17 28161.8 1648.94 8 13181.4 1650.35 18 29810.8 1566.58 9 14831.7 1673.98 19 31377.4 1450.82 10 16505.7 1685.24 20 32828.2 1450.82 表 5 划分结果对比
分界点
个数区间
间隔/s进站
间隔/s出站
间隔/s运行间隔/s 实际线路 18 132.1 261.7 161.3 261.7 划分结果 20 130.1 251.9 147.9 251.9 -
[1] 林瑜筠. 我国发展自动闭塞的探讨[J]. 中国铁路,2004,(10):42-44. [2] Gill D C, Goodman C J. Computer-based optimisation techniques for mass transit railway signalling design[J]. IEE Proceedings B (Electric Power Applications), 1992, 139(3): 261-275. DOI: 10.1049/ip-b.1992.0031
[3] Chang C S, Du D. Further improvement of optimisation method for mass transit signalling block-layout design using differential evolution[J]. IEE Proceedings-Electric Power Applications, 1999, 146(5): 559-569. DOI: 10.1049/ip-epa:19990223
[4] Ke B R, Chen M C, Lin C L. Block-layout design using MAX–MIN ant system for saving energy on mass rapid transit systems[J]. IEEE Transactions on Intelligent Transportation Systems, 2009, 10(2): 226-235. DOI: 10.1109/TITS.2009.2018324
[5] 刘海东,毛保华,王保山,等. 基于差分进化算法的高速铁路区间信号布置优化方法研究[J]. 铁道学报,2013,35(5):40-46. [6] 王丹彤,倪少权,张文泉. 基于整体分布优化算法的闭塞分区划分优化[J]. 铁路计算机应用,2016,25(6):48-51. [7] 王 瑞,陈永刚. 基于捕食搜索策略的粒子群算法求解高铁闭塞分区划分问题[J]. 铁道标准设计,2016,60(1):131-135. [8] 左政伟. 基于模拟退火算法的铁路闭塞分区优化研究[D]. 兰州:兰州交通大学,2013. [9] 刘菁华. 基于RailML的铁路区间信号工程设计方法研究[D]. 北京:北京交通大学,2017. [10] Kang R W, Wang J F, Cheng J F, et al. Intelligent forecasting of automatic train protection system failure rate in China high-speed railway[J]. Eksploatacja i Niezawodność-Maintenance and Reliability, 2019, 21(4): 567-576. DOI: 10.17531/ein.2019.4.5
[11] Zhang C T, Gao Y, Li W J, et al. Robust train scheduling problem with optimized maintenance planning on high-speed railway corridors: the China case[J]. Journal of Advanced Transportation, 2018, 2018(Pt.5): 6157192.
[12] Zhang X, Nie L. Integrating capacity analysis with high-speed railway timetabling: a minimum cycle time calculation model with flexible overtaking constraints and intelligent enumeration[J]. Transportation Research Part C:Emerging Technologies, 2016 (68): 509-531. DOI: 10.1016/j.trc.2016.05.005
[13] 张岳松,田长海,姜昕良,等. 高速铁路列车间隔时间的计算方法[J]. 中国铁道科学,2013,34(5):120-125. [14] Zhang H, Wang J F, Zhang X Y, et al. A method on improving the carrying capacity for CTCS-3 railway[J]. IEEE Intelligent Transportation Systems Magazine, 2021, 13(3): 118-130. DOI: 10.1109/MITS.2019.2962142
[15] 田长海,张守帅,张岳松,等. 高速铁路列车追踪间隔时间研究[J]. 铁道学报,2015,37(10):1-6.




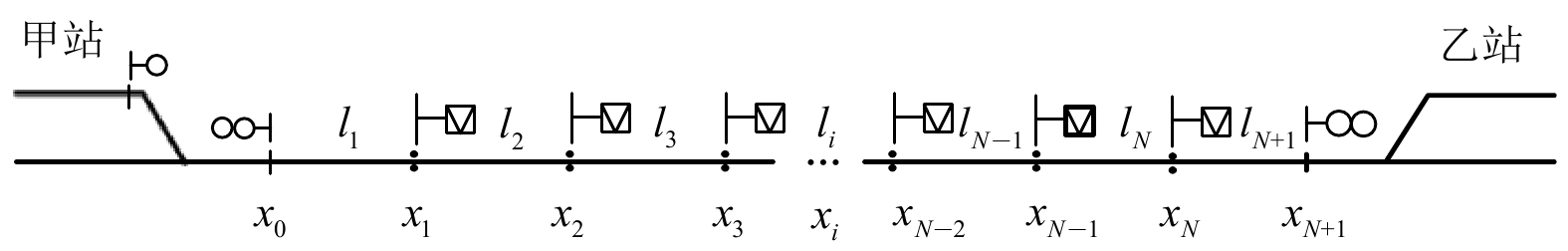
 下载:
下载: