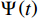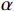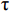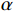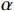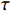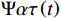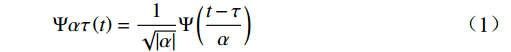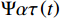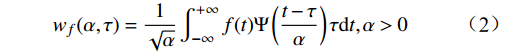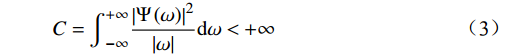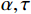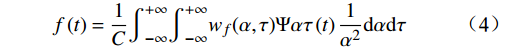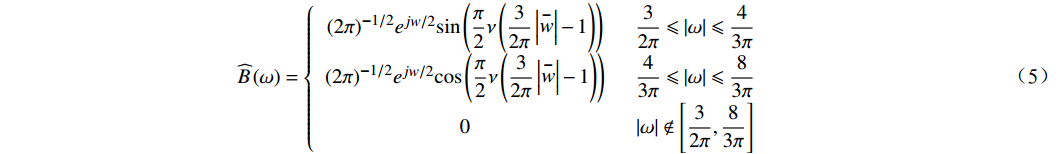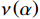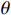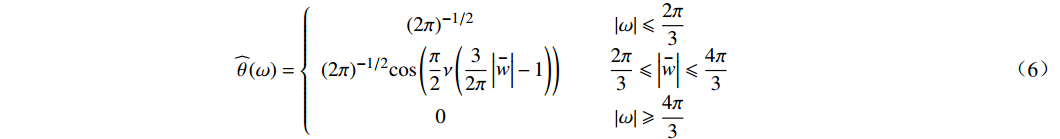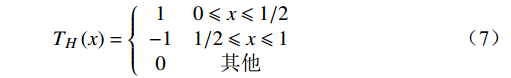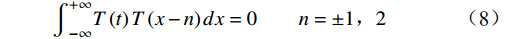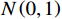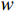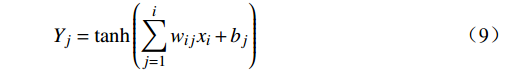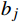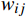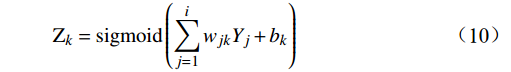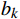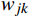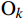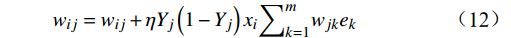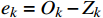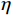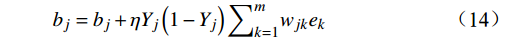Fault detection method for switch machine based on Back Propagation(BP) neural network
-
摘要:
为提高城市轨道交通中ZDJ9型转辙机故障维修效率，提出基于反向传播（BP，Back Propagation）神经网络的转辙机故障检测方法。文章深入分析转辙机动作电流采集原理及现场转辙机转换过程中不同阶段电流曲线特征，确定故障电流曲线种类；对转辙机转换过程中动作电流曲线进行小波分解与重构，对重构后的曲线进行关键特征值提取，将其作为基于BP神经网络的故障检测模型训练数据，最终经过8 000次迭代训练后，故障检测模型的故障检测准确率达到96%，表明该方法能够有效检测转辙机故障及其故障类型。
Abstract:To improve the maintenance efficiency of ZDJ9 type switch machine in urban rail transit, this paper proposed a fault detection method for switch machines based on Back Propagation (BP) neural networks. The paper deeply analyzed the principle of collecting action current of the switch machine and the characteristics of current curves at different stages during the on-site switch machine conversion process, determined the type of fault current curve, performed wavelet decomposition and reconstruction on the action current curve during the switch machine conversion process, extracted key feature values from the reconstructed curve, and used them as training data for the fault detection model based on BP neural network. Finally, after 8 000 iterations of training, the fault detection accuracy of the model reaches 96%, it indicates that this method can effectively detect switch machine faults and their types.
-
转辙机是城市轨道交通信号设备的关键装置，对行车安全起着至关重要的作用。转辙机故障造成列车晚点，影响正常行车、客运组织，其故障处理效率直接影响运营效率[1]。
ZDJ9型转辙机是借鉴了国内外成熟的先进技术、结合我国线路和道岔的实际情况进行优化设计、并根据道岔的不同转换动程和转换力而开发的系列产品。随着ZDJ9 型转辙机使用时间不断增加，在实际运用中有一定概率会产生空转等故障，降低了铁路运输的安全性[2]。
为了缩短道岔故障维修时间，电务人员通常会对道岔故障类型进行分类并给出合理的维修建议。当发生故障时，电务人员需要查看转辙机综合监测系统中转辙机的动作电流值来初步判定故障类型、定位故障位置，再使用万用表测试电压，对故障进行精确定位[3]。这种故障出现后由电务人员定位故障点的维修模式已不能满足轨道交通对设备故障快速维修的要求[4]。
保障运输效率是城市轨道交通线路核心任务，而通过增加新设备提升转辙机故障检测效率不符合实际运营需求。因此，本文在不改变既有信号设备配置的基础上，提出基于反向传播（BP，BackPropagation）神经网络的转辙机故障检测方法。将ZDJ9型转辙机故障原因、转辙机动作电流曲线与故障类型一一对应并对转辙机动作电流进行小波变换，突出电流曲线关键特征。搭建基于BP神经网络的转辙机故障检测模型，根据转辙机动作电流曲线特征，多维度选取电流曲线特征值，训练转辙机故障检测模型，通过正向训练、反向验证及多次迭代训练来提升故障检测的准确率，实现快速检测和定位转辙机故障点、提升运营效率的目的。
1 转辙机故障与动作电流的关系分析
1.1 采集电路分析
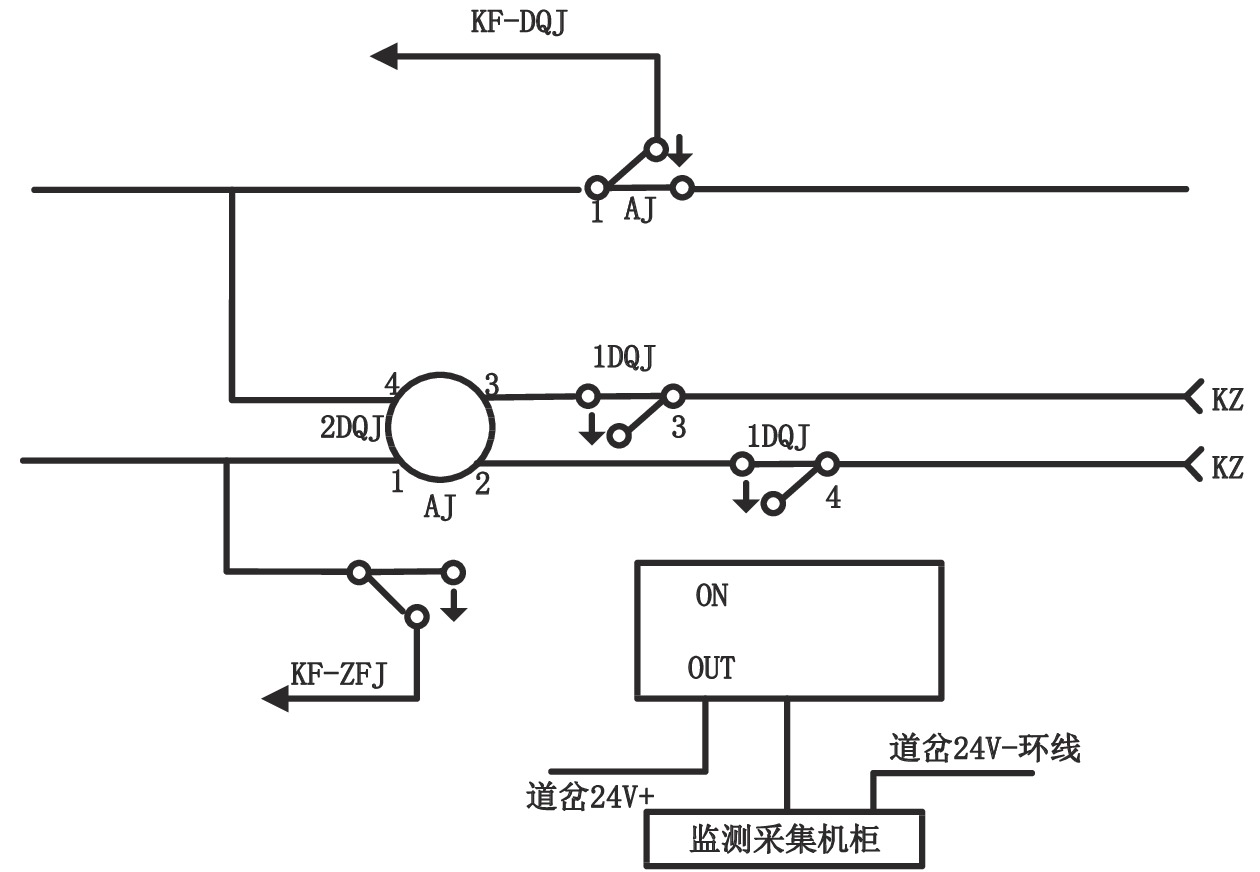
结合现场调研和实际应用，电务人员主要依靠转辙机的动作电流曲线来进行故障判断[5]。转辙机动作电流采集原理如图1所示。
转辙机综合监测系统通过采集1DQJ的后节点条件来采集记录转辙机的动作电流曲线。道岔有动作意图后，1DQJ励磁吸起，采集机以40 ms/次的频率开始记录道岔动作电流，并以此时间作为动作开始时间[6]。
1.2 动作电流曲线分析
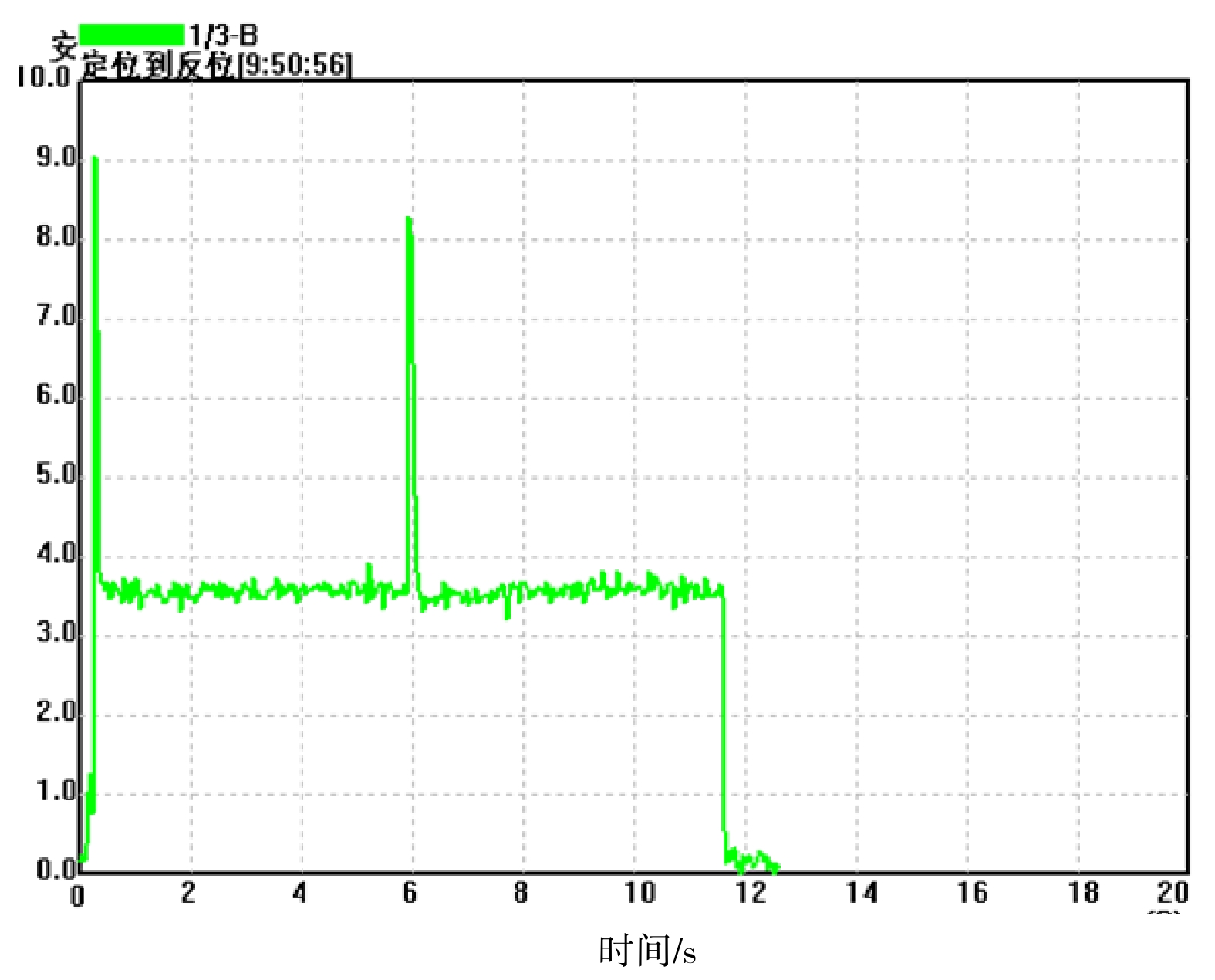
如图2所示，道岔正常转换时，转辙机动作电流曲线特征可分为如下3个阶段。
（1）解锁阶段：当转辙机收到启动命令后2DQJ转级，这时会出现一个较大的启动电流完成道岔解锁。
（2）动作阶段：在这个阶段尖轨在滑床板上做横向移动，动作电流为一条平滑的曲线。
（3）缓放阶段：在此阶段，道岔转换完毕，自动开闭器节点闭合。由于在该阶段交流转辙机电源还在向外输出380 V电压，由于开闭器节点闭合，导致一相电源提速断开，剩下两相电源通过室外表示电路构成回路，因此产生一个小尾巴电流。
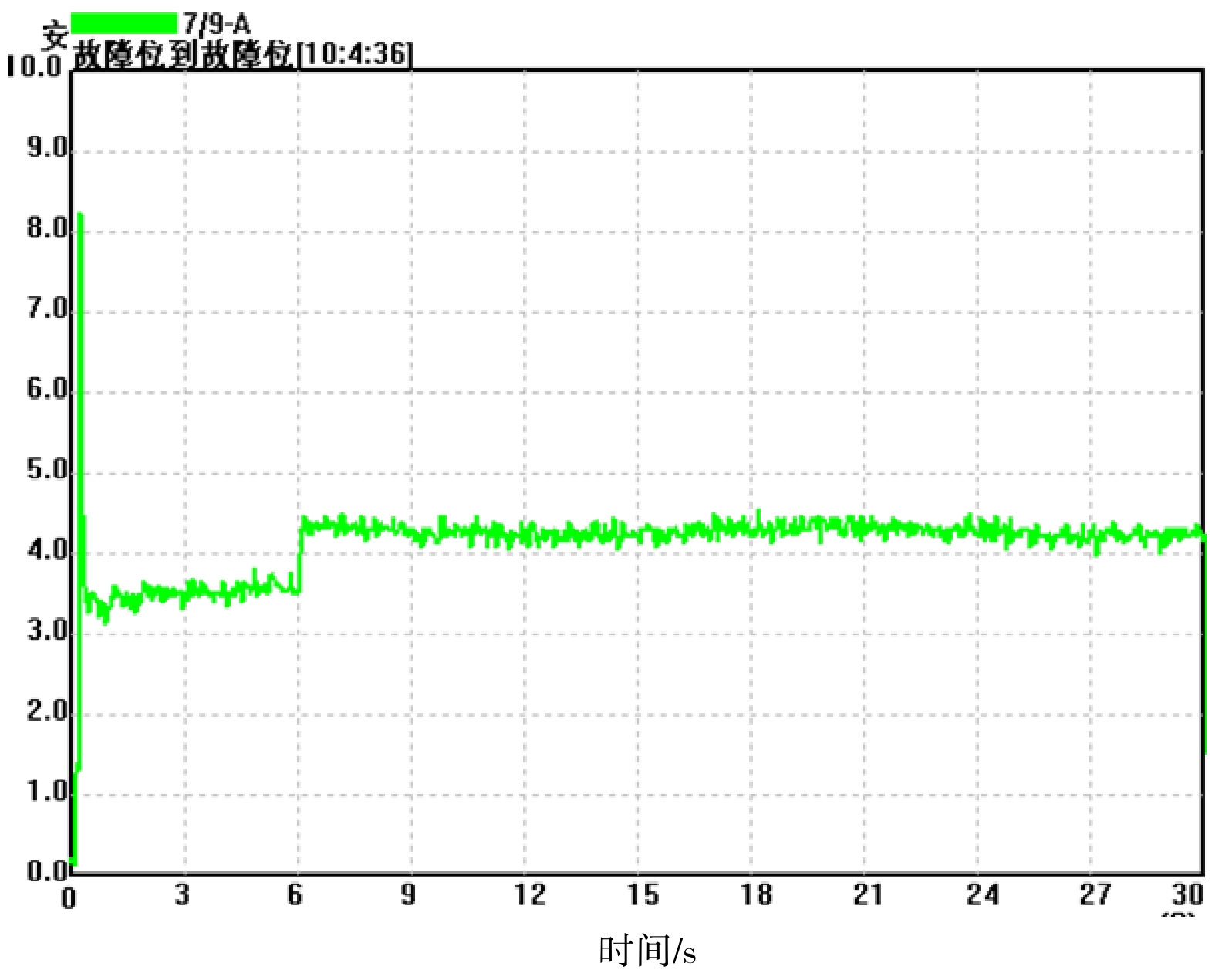
图3为ZDJ9型转辙机现场空转故障时的电流曲线。正常工作曲线相比空转故障时的动作时间较长，没有在规定时间内锁闭。结合现场经验，常见的故障原因是道岔尖轨与基本轨之间夹有异物。
1.3 现场故障统计
由于现场道岔工作环境复杂，因此转辙机故障种类也多种多样。通过收集现场ZDJ9型转辙机的故障数据，结合其工作原理，总结出转辙机故障类型及原因，如表1所示。
表 1 ZDJ9型转辙机故障故障类型及原因故障类型 原因 空转故障 尖轨卡阻、杆件卡阻、未解锁 或内卡阻 缓放阶段无“小尾巴”故障 转辙机卡缺口故障或SH2转换锁闭器故障、
室外整流二极管开路缓放阶段“小尾巴”数值变高 室外二极管击穿 缓放阶段“小尾巴”数值和动作
阶段大小相近室外电阻短路 缓放阶段“小尾巴”数值偏低 室外电阻或二极管特性不良 2 相关技术
2.1 小波分解与重构
小波分解与重构技术是一种信号处理方法，常用于对非平稳信号进行分析和重构。它是基于小波变换的一种扩展，可以更好地捕捉信号的时频域特性。小波分析由于具有多分辨率分析的特点，所以能够聚焦到信号的任意细节进行多分辨率的时频域分析。
设
$ \mathrm{\Psi }\left({t}\right) $ ∈L2（R） 为一个基本母小波，其中，L2（R）为一个函数线性空间；$ \alpha $ ,$ \text{τ} $ ∈R，$ \alpha $ ≠0。经过伸缩$ \alpha $ 尺度，$ \tau $ 位移后，得到连续小波$ \mathrm{\Psi }\alpha \tau \left({t}\right) $ $$ \mathrm{\Psi }\alpha \tau \left({t}\right) = \frac{1}{\sqrt{\left|\alpha \right|}}\mathrm{\Psi }\left(\frac{{t}-\tau }{\alpha }\right) $$ (1) 将L2（R）空间的函数ƒ（t）与连续小波
$ \mathrm{\Psi}\alpha\tau\left(\mathit{\mathrm{\mathit{t}}}\right) $ 进行卷积，可得到函数ƒ（t）的连续小波变换为$$ w_f(\alpha, \tau)=\frac{1}{\sqrt{\alpha}} \int_{-\infty}^{+\infty} f({t}) \Psi\left(\frac{{t}-\tau}{\alpha}\right) \tau {\mathrm{d}}t, \alpha>0$$ (2) 假设ƒ（t）∈L2（R），若满足波函数Ψ（ω）在全体实数范围内有限的某种加权平均能量或概率密度为
$$ {C}={\int }_{-\infty }^{+\infty }\frac{{\left|\mathrm{\Psi }\left(\omega \right)\right|}^{2}}{\left|\omega \right|}{\mathrm{d}}\omega < +\infty $$ (3) 则可得到频域内等效为
为保证重构信号的精度，需要将
$ \alpha ,\tau $ 的取值尽量小，否则信号重构的精度会变低。$$ f\left({t}\right)=\frac{1}{{C}}{\int }_{-\infty }^{+\infty }{\int }_{-\infty }^{+\infty }{w}_{{f}}(\alpha ,\tau )\mathrm{\Psi }\alpha \tau \left({t}\right)\frac{1}{{\alpha }^{2}}{\mathrm{d}}\alpha {\mathrm{d}}\tau $$ (4) 2.2 BP神经网络
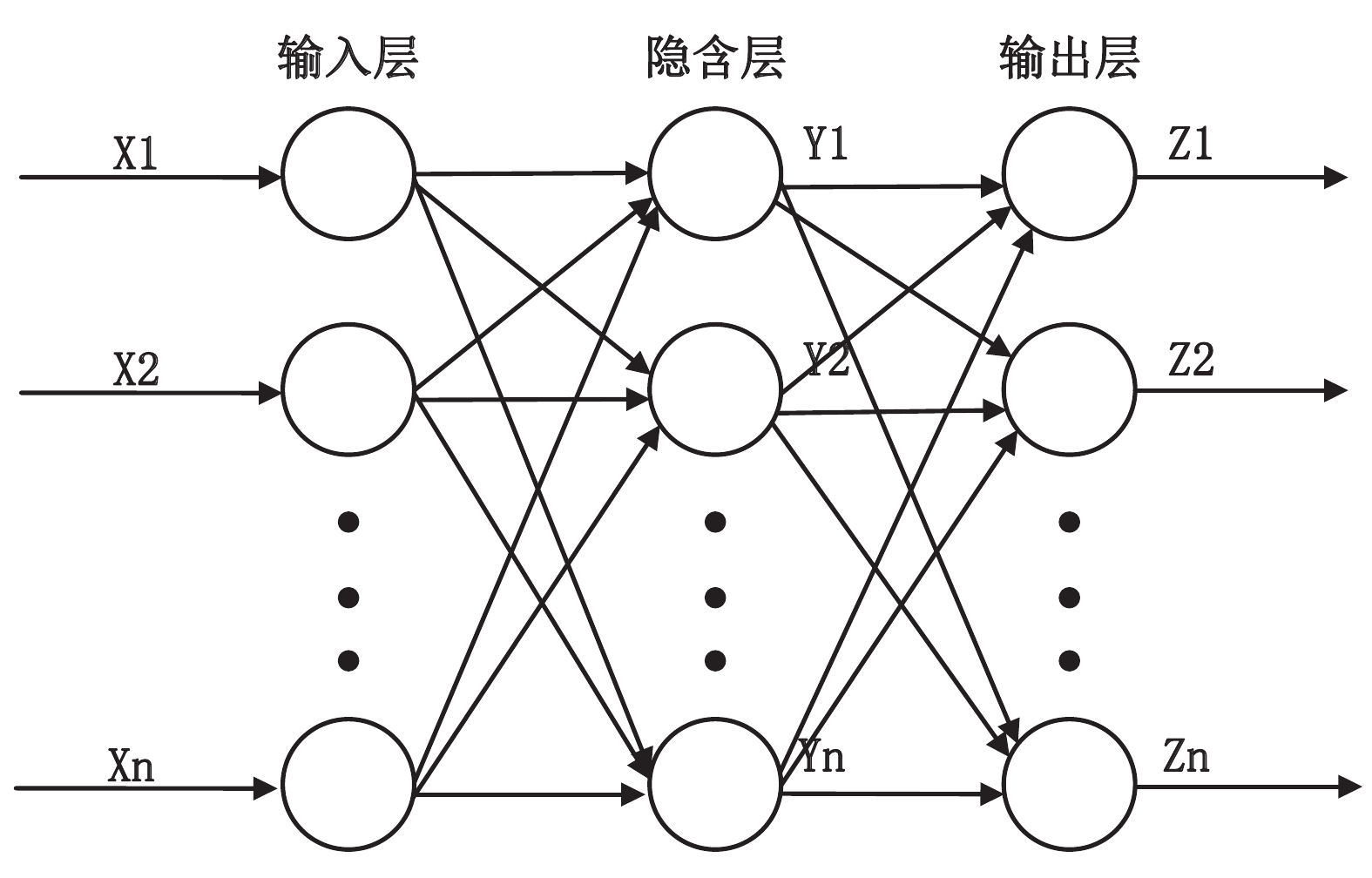
BP神经网络是一种使用了反向传播算法的神经网络，是一个每次根据训练得到的结果与预想结果进行误差分析，进而修改权重和阈值，一步一步得到能输出和预想结果一致的模型。BP神经网络无论在网络理论还是在性能方面已比较成熟。其突出优点就是具有很强的非线性映射能力和柔性的网络结构。网络的中间层数、各层的神经元个数可根据具体情况任意设定，并且随着结构的差异其性能也有所不同[7]。BP神经网络结构如图4所示。
BP神经网络的过程主要分为2个阶段，第1阶段是信号的前向传播，从输入层经过隐含层，最后到达输出层；第2阶段是误差的反向传播，从输出层到隐含层，最后到达输入层，依次调节隐含层到输出层的和偏置，输入层到隐含层的权重和偏置[8]。
3 转辙机故障检测模型
3.1 模型设计
提取转辙机综合监测系统应用道岔动作电流曲线，对曲线进行小波分解与重构，并提取关键特征值。搭建基于BP神经网络的转辙机故障检测模型，将小波重构后提取的特征值作为该模型的输入，经过正向训练与反向验证，得出检测结果，帮助维护人员快速检测、定位故障点。
转辙机故障检测模型如图5所示。将转辙机综合监测系统的转辙机动作电流曲线进行小波分解与重构，经过小波分解后电流曲线相关特征更加明显[9]，提取重构细节信号的特征作为转辙机故障检测模型的训练数据。
3.2 小波分解设计
为避免转辙机动作电流自身的增减趋势及相同类型的道岔不同使用环境带来的干扰，根据转辙机动作曲线特征，选取Meyer、Haar小波函数对转辙机曲线特征进行分解与重构。
Meyer小波函数定义为：
$$ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \widehat{B }\left(\omega \right)=\left\{\begin{array}{cc}{\left(2\pi \right)}^{-1/2}{e}^{jw/2}\mathrm{sin}\left(\dfrac{\pi }{2}\nu \left(\dfrac{3}{2\pi }\left|\stackrel-{w}\right|-1\right)\right)& \;\;\dfrac{3}{2\pi }\leqslant\left|\omega \right|\leqslant\dfrac{4}{3\pi }\\ {\left(2\pi \right)}^{-1/2}{e}^{jw/2}\mathrm{cos}\left(\dfrac{\pi }{2}\nu \left(\dfrac{3}{2\pi }\left|\stackrel-{w}\right|-1\right)\right)& \;\;\dfrac{4}{3\pi }\leqslant\left|\omega \right|\leqslant\dfrac{8}{3\pi }\\ 0& \;\;\left|\omega \right|\notin \left[\dfrac{3}{2\pi },\dfrac{8}{3\pi }\right]\end{array}\right. $$ (5) 式（5）中，
$ \nu \left(\alpha \right) $ 为构造Meyer小波的辅助函数，设$ \theta $ 为尺度函数，则有$$ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \widehat{\theta }\left(\omega \right)=\left\{\begin{array}{cc}{\left(2\pi \right)}^{-1/2}& \left|\omega \right|\leqslant\dfrac{2\pi }{3}\\ {\left(2\pi \right)}^{-1/2}\mathrm{cos}\left(\dfrac{\pi }{2}\nu \left(\dfrac{3}{2\pi }\left|\stackrel-{w}\right|-1\right)\right)& \;\;\;\;\;\;\dfrac{2\pi }{3}\leqslant\left|\stackrel-{w}\right|\leqslant\dfrac{4\pi }{3}\\ 0& \left|\omega \right|\geqslant \dfrac{4\pi }{3}\end{array}\right. $$ (6) Haar 小波定义如下：
$$ T_H\left(x\right)=\left\{\begin{array}{cc}1 & 0\leqslant x\leqslant1/2 \\ -1 & 1/2\leqslant x\leqslant1 \\ 0 & 其他\end{array}\right. $$ (7) Haar为正交小波，即
$$ {\int}_{-\infty}^{+\infty} T \left(t\right) T \left(x-n\right)dx=0\qquad n=\pm 1 \text{，}2 $$ (8) 3.3 转辙机故障检测模型训练
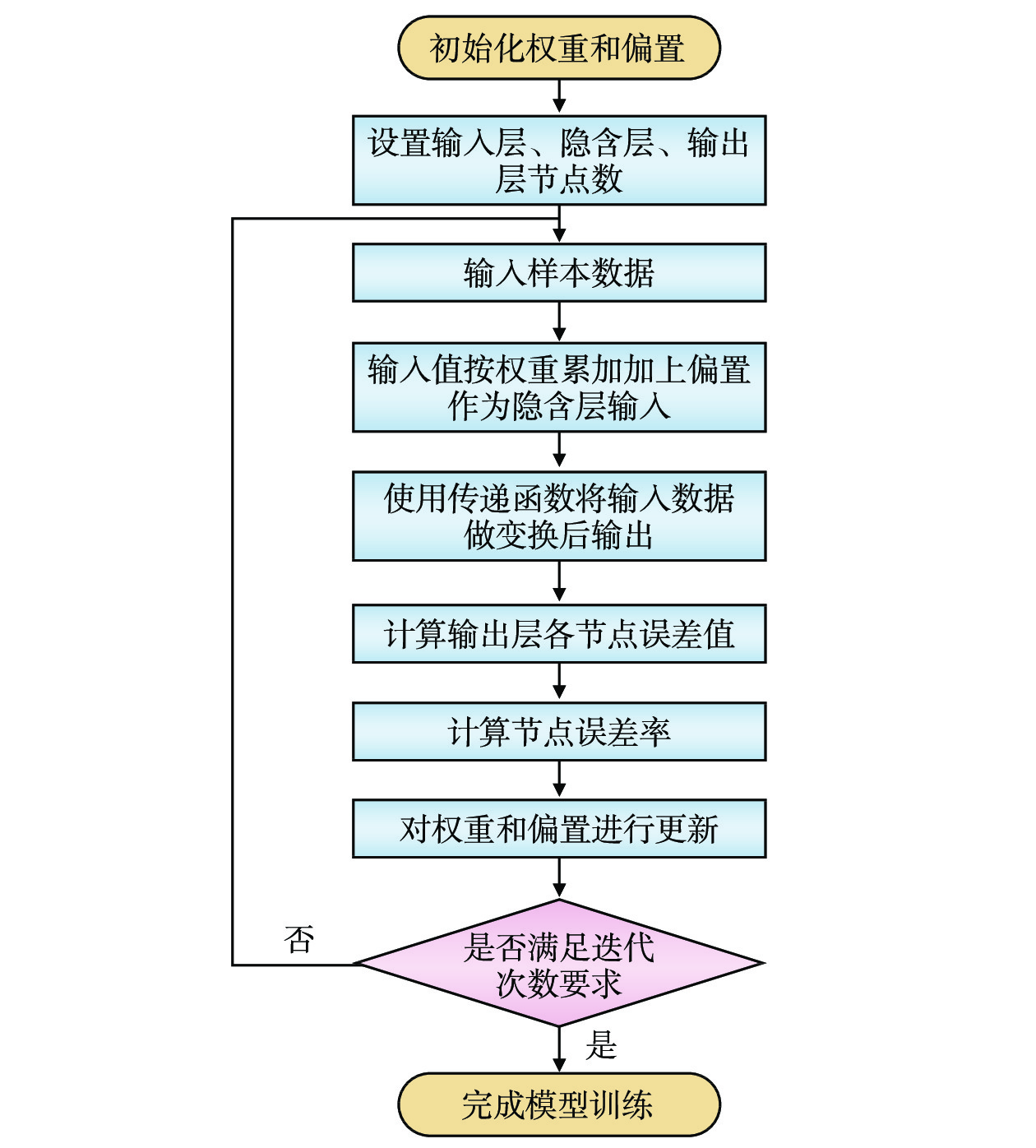
基于BP神经网络的转辙机故障检测模型训练流程如图6所示，针对本次设计，对服从正态分布
$ N\left(\mathrm{0,1}\right) $ 进行随机采样来初始化权重$ w $ ，以全0初始化偏置$ b $ 。提取12个特征值作为BP神经网络的输入值，故输入层的节点数为12，将隐含层节点数设置为6，输出层节点数为5。使用tanh作为第1层的激活函数，使用sigmoid作为第2层的激活函数。
隐含层的输出为
$$ {Y}_{j}=\mathrm{tanh}\left(\sum _{j=1}^{i}{w}_{ij}{x}_{i}+{b}_{j}\right) $$ (9) 式（9）中，
$ {b}_{j} $ 为输入层到达隐含层的偏置，$ {w}_{ij} $ 为输入层到达隐含层的权重。输出层的输出为
$$ \mathrm{Z}_k=\operatorname{sigmoid}\left(\sum_{j=1}^i w_{j k} Y_j+b_k\right)$$ (10) 式（10）中，
$ {b}_{k} $ 为隐含层到达输出层的偏置，$ {w}_{jk} $ 为隐含层到达输出层的权重。误差的计算公式为
$$ \mathrm{{\rm E}}=\frac{1}{2}\sum _{k=1}^{m}{\left({\mathrm{{\rm O}}}_{k}-{Z}_{k}\right)}^{2} $$ (11) 式（11）中，
$ {\mathrm{{\rm O}}}_{k} $ 为期望输出。权重更新公式为
$$ {w}_{ij}={w}_{ij}+\eta {Y}_{j}\left(1-{Y}_{j}\right){x}_{i}{\sum }_{k=1}^{m}{w}_{jk}{e}_{k} $$ (12) $$ {w}_{jk}={w}_{jk}+\eta {Y}_{j}{e}_{k} $$ (13) 式（12）、式（13）中，
$ e_k=O_k-Z_k $ ，$ \eta $ 为学习率，设置为0.0075，偏置更新公式为$$ {b}_{j}={b}_{j}+\eta {Y}_{j}\left(1-{Y}_{j}\right){\sum }_{k=1}^{m}{w}_{jk}{e}_{k} $$ (14) $$ {b}_{k}={b}_{k}+\eta {e}_{k} $$ (15) 4 实验与验证
4.1 波形重构
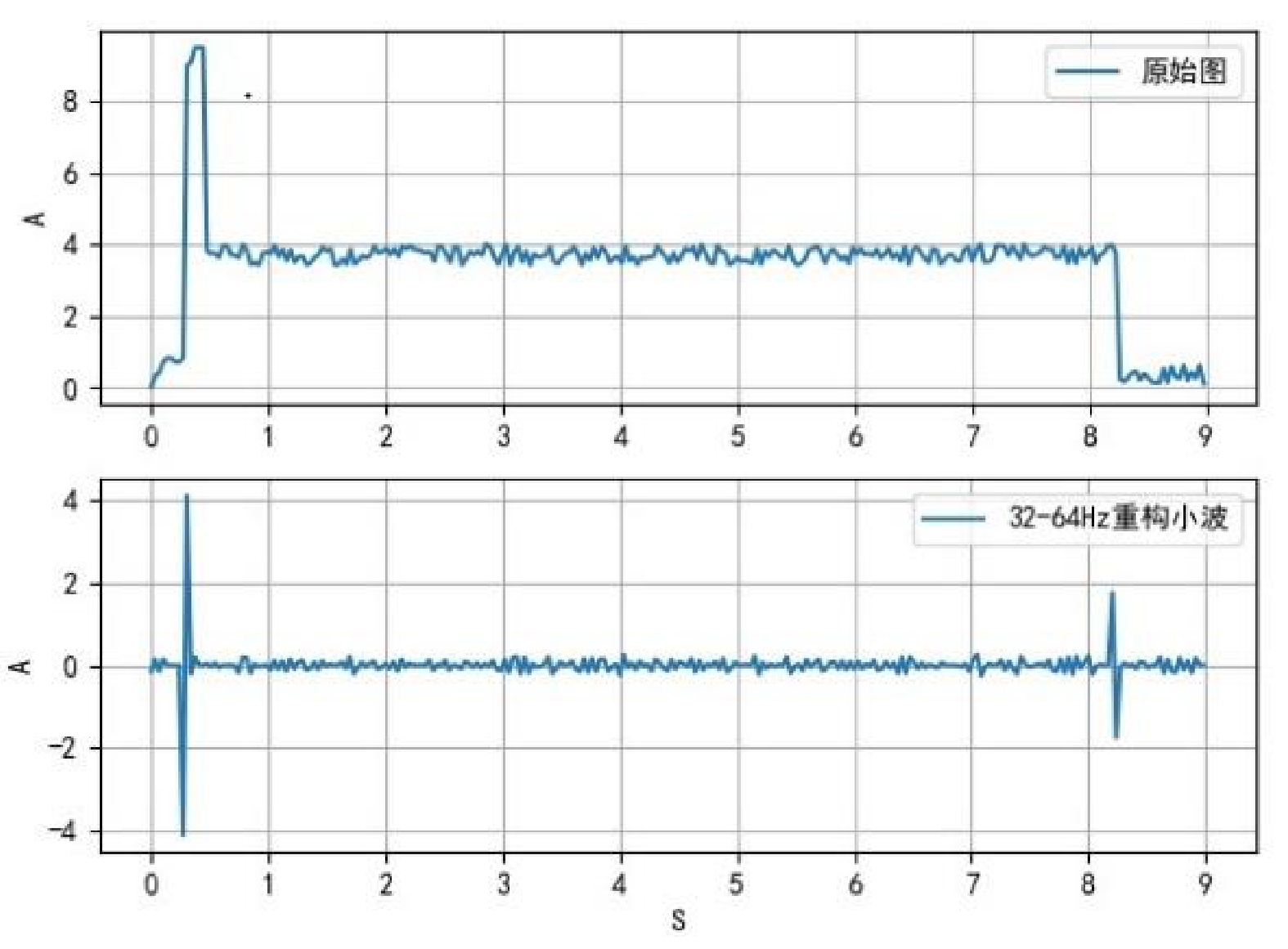
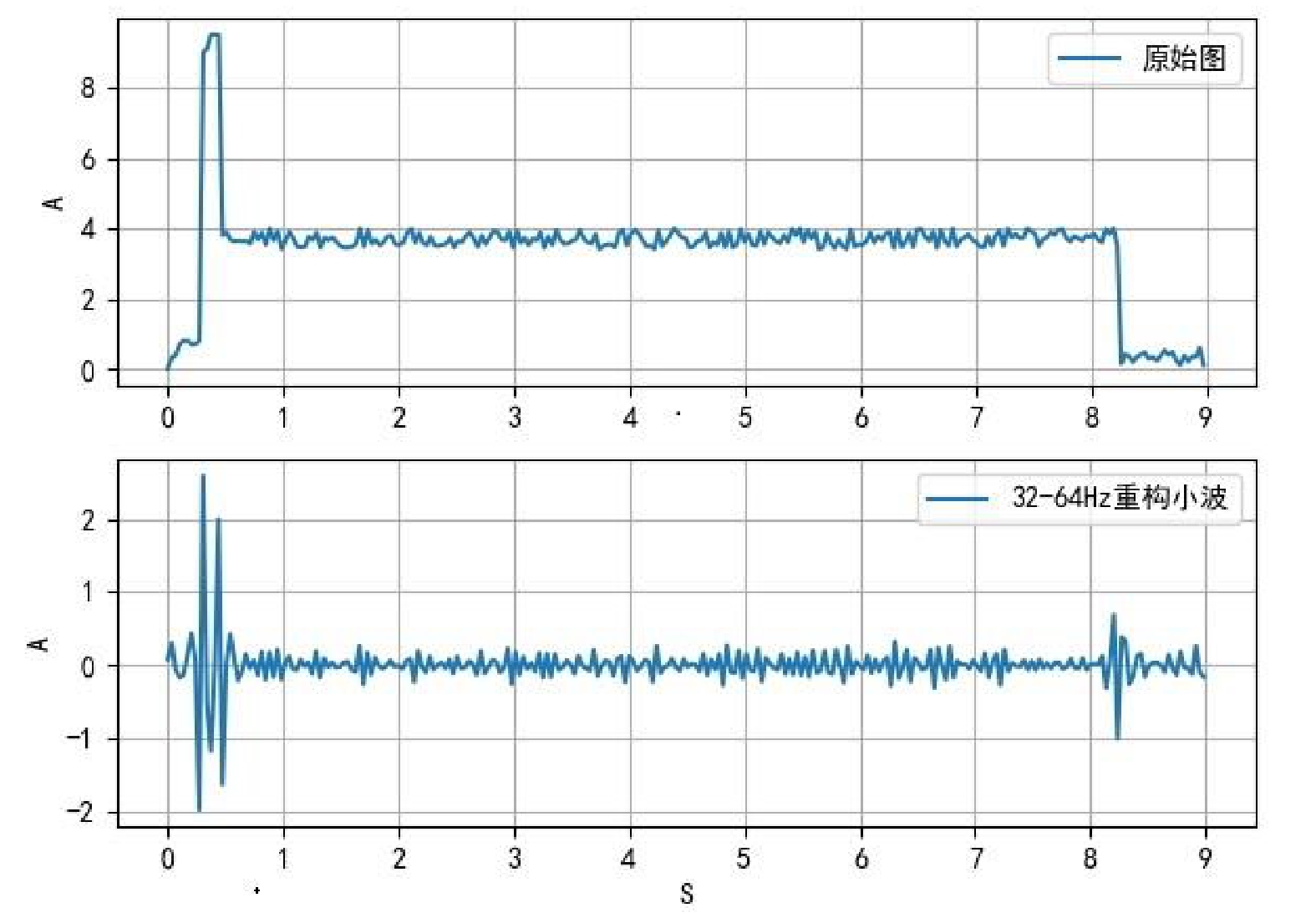
图7、图8是对缓放阶段“小尾巴”数值偏低的转辙机动作电流曲线在Meyer、Haar小波函数下的32～64 Hz重构小波，图中的横坐标为时间，纵坐标为电流值。
如图7、图8所示，原始图中包含了部分的细节和噪声，经过小波分解与重构后的图像增强了信号细节特征，将其他信号重构的更加平滑，消除了局部信号干扰根据原始电流图特征，选择在32～64 Hz频率范围内对原始图进行小波分解与重构。在进行小波分解时，会得到一系列高频和低频子图像，将高频图像和低频图像进行合并，即得到了重构后的图像。
4.2 特征提取
对重构图像进行特征提取，分析其时域指标及频域指标。选取重构细节信号的标准差、方差、平均值、均方根、峭度指标、偏斜度、最大值、方根幅值、峰值因子、裕度因子、波形因子、脉冲指数等12个指标作为特征量。
以道岔空转为例，转辙机电流曲线图经过Haar小波分解与重构后，对其进行特征提取，如表2所示，通过自定义输出值含义，将转辙机电流曲线特征值与转辙机故障状态进行对应。
表 2 道岔空转特征值特征值名称 特征值 输出值含义 标准差 0.316 00001
（道岔空转故障）方差 0 平均值 0 均方根 0.315 峭度指标 33.926 偏斜度 0.052 最大值 2.627 方根幅值 0.125 峰值因子 8.337 裕度因子 0.125 波形因子 21.005 脉冲指数 1.901 4.3 转辙机故障检测模型训练
结合现场实际情况定义输出值含义，例如：输出值00000代表正常动作，00001代表空转故障电流，00010代表无“小尾巴”电流，00100代表“小尾巴”电流超标线01000代表“小尾巴”电流突变，10000代表“小尾巴”电流偏低。设置迭代次数为10000，进行模型训练。
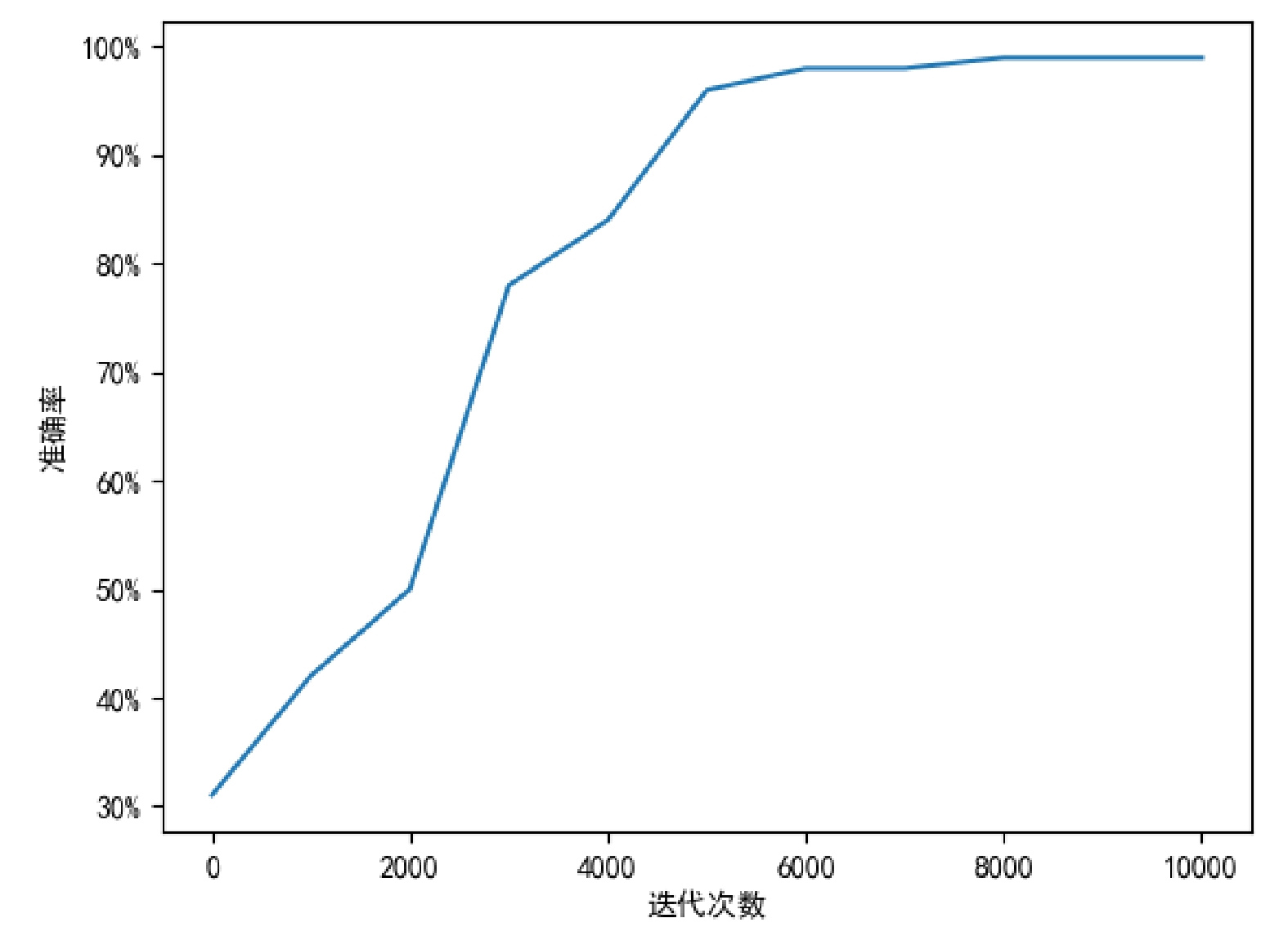
使用Matlab进行模型训练。训练的数据来自于实际运营线路中ZDJ9型转辙机监测系统记录的动作电流日志，以及在实验室环境中模拟特定的转辙机故障时监测到的动作电流曲线。共选择20 000条ZDJ9转辙机动作电流曲线作为样本，训练结果如图9所示。随着迭代次数的增加，转辙机故障检测模型的准确率也随之提升，说明该模型的学习率、初始权重与偏置、传递函数、迭代次数、误差传播函数的选择符合预期要求，没有产生过拟合与欠拟合情况。当迭代次数达到8 000次时，其模型的预测准确率达到了96%以上，设置迭代次数最大为10 000，这时认为该模型已经收敛，停止继续训练，防止出现过拟合。
5 结束语
针对现场实际情况，本文提出一种基于BP神经网络的转辙机故障检测方法，该方法能够实现较高的故障检测准确率，有效解决现场转辙机故障维修不及时的问题。实现高效准确的设备故障检测是智慧交通建设的主要方向，在本文研究的基础上，将在轨道交通领域收集更多的设备运行状态数据，进一步开展模型训练与验证，将该技术推广应用到其他关键运营设备设施故障的检测工作中。
-
表 1 ZDJ9型转辙机故障故障类型及原因
故障类型 原因 空转故障 尖轨卡阻、杆件卡阻、未解锁 或内卡阻 缓放阶段无“小尾巴”故障 转辙机卡缺口故障或SH2转换锁闭器故障、
室外整流二极管开路缓放阶段“小尾巴”数值变高 室外二极管击穿 缓放阶段“小尾巴”数值和动作
阶段大小相近室外电阻短路 缓放阶段“小尾巴”数值偏低 室外电阻或二极管特性不良 
下载: 导出CSV
表 2 道岔空转特征值
特征值名称 特征值 输出值含义 标准差 0.316 00001
（道岔空转故障）方差 0 平均值 0 均方根 0.315 峭度指标 33.926 偏斜度 0.052 最大值 2.627 方根幅值 0.125 峰值因子 8.337 裕度因子 0.125 波形因子 21.005 脉冲指数 1.901
下载: 导出CSV
-
[1] 占雪梅,楚彩虹. ZDJ9型道岔转辙机故障分析处理[J]. 郑州铁路职业技术学院学报,2023,35(3):35-37. [2] 朱孟雯. ZYJ7型提速道岔故障诊断系统研究[D]. 成都:西南交通大学,2016. [3] 宋文渊. 大秦线道岔微机监测电流及功率曲线的分析与研究[J]. 太原铁道科技,2019(12):10-13. [4] 齐小民,贺玉芹,刘晓明. 道岔健康状态评估管理系统的研究应用[J]. 铁道通信信号,2020,56(8):21-24. [5] 史宏力. ZYJ7型液压道岔控制电路故障分析[J]. 科技创新与应用,2020(10):119-120. [6] 张 星. 基于相似度的道岔故障电流曲线识别方法研究与实现[D]. 兰州:兰州交通大学,2016. [7] 张梦琪,赵会兵,孙上鹏. 基于粒子群支持向量机的轨道电路分路不良预测方法[J]. 铁道学报,2015,37(10):68-74. [8] 周志华. 机器学习[M]. 北京:清华大学出版社,2016. [9] 王东升. 人工智能在铁路信号故障诊断中的应用研究[J]. 科技风,2020(17):123-124. -
期刊类型引用(1)
1. 孙笑笑，江本赤，陈智君，李公文. 基于数字孪生与BP神经网络的RV减速器故障诊断. 安徽科技学院学报. 2025(02): 104-111 . 
百度学术
其他类型引用(0)
计量
- 文章访问数: 97
- HTML全文浏览量: 24
- PDF下载量: 28
- 被引次数: 1
