Optimization of subway platform's passenger flow guidance methodbased on AnyLogic
-
摘要: 为避免地铁车厢客流过度集中,引导站台乘客分散乘车,文章以地铁各车厢客流均衡为目标,以均衡度标准差为指标,综合考虑车厢现有人数、候车人数及预计下车人数,优化地铁站台客流引导方式。通过AnyLogic仿真软件,模拟广州地铁珠江新城5号线站台条件,对比了客流量范围在12万人/日~60万人/日条件下,不同引导方式对车厢乘客分布不均衡度的影响。结果表明,地铁站客流量达到24万人/日时,考虑预计下车人数的站台客流引导方式下的车厢客流均衡度标准差明显提升;与不考虑该站下车人数的引导方式相比,客流均衡度标准差提升幅度最大达到25.6%,相比人工引导方式的提升幅度达53.6%,有效提升了地铁精细化服务能力。
-
关键词:
- 城市轨道交通 /
- 地铁站台 /
- 客流引导 /
- AnyLogic仿真 /
- 均衡度标准差
Abstract: In order to avoid excessive concentration of passenger flow in subway carriages and guide passengers on the platform to disperse and board trains, this paper aimed to balance the passenger flow in each carriage of the subway, used the standard deviation of balance degree as an indicator, comprehensively considered the existing number of passengers in the carriage, the number of waiting passengers, and the expected number of alighting passengers, to optimize the subway platform passenger flow guidance method. Through AnyLogic simulation software, the paper simulated the platform conditions of the Pearl River New Town Line 5 of Guangzhou Metro, and compared the influence of different guidance modes on the uneven distribution of passengers in the carriage under the conditions of passenger flow ranging from 120 000 people/day to 600 000 people/day. The results show that when the passenger flow of the subway station reaches 240 000 people/day, the standard deviation of the passenger flow balance of the carriages under the platform passenger flow guidance method considering the expected number of passengers getting off significantly improves. Compared with the guidance method that does not consider the number of passengers getting off at the station, the standard deviation of passenger flow balance has increased by a maximum of 25.6%, and compared to the manual guidance method, the improvement has reached 53.6%. The optimized guidance method effectively improves the refined service capacity of the subway. -
据广州地铁年报统计数据[1],截至2022年12月31日,广州地铁在运营线路27条、运营站点474站,运营里程达857 km,2022年客运总量达235794万人次,占全市公共交通出行总量的63%,广州地铁已连续6年日均客流量超600万人次。为避免车厢间客流量差异过大,更有效地运用整列列车的容量,引导地铁站台客流、缓解乘客分布不均衡已成为城市轨道交通客流组织中亟需解决的问题。
我国学者田金洪等人[2]通过计算各车厢拥挤度,引导下一站台上的乘客进行车厢的选择;王世秩等人[3]通过采集地铁列车运营过程中的ATS(Automatic Train Supervision)等数据,计算车厢实时拥挤度,引导乘客上下车;庞梦圆等人[4]通过图像采集获取车厢拥挤度,并采用时间序列预测法对整车下车率进行了预测,以此引导乘客上下车。国际上,ÇAPALAR J等人[5]通过压力传感器获取各节车厢乘客数,引导乘客选择客流量较少的车厢;DING H等人[6]基于城市轨道交通平台建立了一种地铁乘坐引导模型,以乘客分布情况为指标引导乘客选择车厢;ZHENG Z等人[7]提出了站台屏蔽门客流实时拥堵测量系统,通过监控视频识别屏蔽门处的拥堵事件,避免站台乘客堆积。
以上研究大多以各车厢现有拥挤度为判断依据,缓解客流不均衡的情况,但未能考虑各节车厢下车人数对乘客分布不均衡度的影响,而地铁各节车厢的留存人数才是影响车厢均衡度的关键。因此,本文使用AnyLogic仿真软件,以广州地铁珠江新城站5号线站台为原型,在考虑站台屏蔽门外排队人数、乘客距队列的距离、地铁各车厢已有人数及乘客各节车厢下车人数等影响因素的情况下,模拟地铁运行若干站后乘客分布的变化情况,从而定量验证各节车厢下车人数这一影响因素对乘客分布不均衡度的影响。
1 地铁站台客流引导方式与评价指标
1.1 地铁站台客流引导方式
根据文献[8—9],目前常用的站台引导的方式有2种:引导方式1,即人工引导,当高峰客流到达时,地铁站往往会由站台岗的站务员凭借经验辅助安排乘客上车,该方式为目前地铁站最普遍的现状;引导方式2,即通过各种方式获取来车各车厢内现有拥挤度,并通过站台乘客信息系统(PIS,Passenger Information System),引导乘客选择相对空旷的车厢,该方式被我国部分城市(如深圳)及韩国、新加坡等国的地铁线路上采用,其中,获得较好效果的是新加坡地铁(SMRT)。SMRT在通过车厢拥挤度引导乘客的基础上,还考虑到了已在站台候车的乘客,辅以语音引导的方式,提高了引导的有效性。
基于SMRT及现行的2种引导方式,本文提出了引导方式3,即在获得来车车厢拥挤度及站台各车厢候车人数的情况下,通过预测各车厢到站下车人数(如短期客流预测模型[10]等),综合3方面的条件,来引导乘客合理、快捷地选择候车队列。
1.2 评价指标
地铁车厢客流均衡,是指地铁平均乘客数与各节车厢内乘客数趋近相等,国内外学者普遍采用均衡度方差作为定量衡量的指标[11-12]。然而,随着地铁流量的增大,均衡度方差增长过快,会在同一图表内干扰小客流量时不均衡度的比较。为避免这种情况,本文选择了均衡度标准差(B)作为衡量指标。与均衡度方差类似,B可以通过计算每个车厢乘客数与平均乘客数之间的差异(即偏差),同时可以更加准确地衡量地铁车厢间乘客数量分布的均匀度,避免干扰不均衡度的比较。具体计算公式为
B=1N√1n−1n∑i=1(xi−μ)2 (1) 式(1)中,
xi 表示编号为i的车厢内乘客数;μ 为所有车厢乘客数的均值;N为经过的总车站数;n为车厢数,在我国,其取值通常为6。2 AnyLogic仿真软件与建模方法
2.1 AnyLogic软件介绍
AnyLogic是一款基于Java的仿真建模软件,相对于其他仿真软件,AnyLogic软件采用了混合建模的方法,即可以将不同类型的模型组合在一起,以更准确地描述实际系统的行为。此外,AnyLogic支持高级可视化和动态数据分析,有助于用户更好地理解和解释仿真结果。该软件基于UML和Java语言的建模方法,可帮助用户快速开发、编程,实现模型的动画展示和评价指标的可视化。
本文借助AnyLogic仿真软件对地铁站台客流组织进行建模仿真,主要使用了AnyLogic中的行人库模块及部分轨道库、流程库模块。其中,行人库底层则主要采用社会力模型算法。
2.2 建模方法
社会力模型是一种连续型微观仿真模型,可以给出真实的行人踪迹。该模型基于多粒子自驱动系统的框架,假定组成人群的个体具有思考和对周围环境做出反应的能力。社会力模型算法用社会力的概念来描述人的主观愿望、人与人之间的相互关系,以及人与环境之间的相互影响,仿真软件将乘客的个体行为描述为以下 3 种社会力的共同作用。
(1)自驱力:指模拟个体对目标点的吸引作用,以达成其前往目标的愿望,运动学方程为
d→radt=→va(t) (2) 式(2)中,
→ra 为行人a的空间位置向量;→va(t) 为行人a的速度。(2)人与人之间的作用力:指模拟人群中个体之间的避让行为,以避免碰撞。行人加减速和方向变化方程为
d→radr=→fa(t)+→ξ(t) (3) 式(3)中,
→fa(t) 为社会力;→ξ(t) 为反映随机行为偏差的扰动项。(3)人与墙之间的作用力:模拟个体对周围环境的感知和反应,以寻找可通行的路径。
则社会力方程为
→fa(t)=→f0a(→va)+→fab(→ra)+∑→fab(→ra,→va,→rb,→vb)+∑i→fai(→ra,→ri,t) (4) 式(4)中,
→f0a(→va) 为加速力;→fab(→ra) 为人与墙之间的作用力;∑→fab(→ra,→va,→rb,→vb) 为行人a与其他行人b间的作用力;∑i→fai(→ra,→ri,t) 为吸引效果。3 仿真模型
3.1 模型基本假设
为了降低仿真建模不必要的干扰,有必要进行一定的假设和说明。
(1)考虑到社会力模型中乘客会受到其他乘客、墙壁、候车队列的综合作用力,为简化乘客行为,将乘客所占空间设定为二维圆形,并参考我国人群生理尺寸数据,将直径范围设为0.2 m~0.3 m。
(2)假设在候车的过程中,乘客均按序排队上车,无插队、队伍间切换、候车途中离站及放弃本次列车的情况。
(3)假设行人在其他条件相同的情况下,倾向于选择距离最近车厢为优先候车队列。
(4)根据文献[4],超80%的乘客希望行走的距离在50 m以内,有70%左右的乘客愿意走一定的距离而去宽松的车厢,有接近90%的乘客希望有对于车厢内客流信息的提示来引导乘客更加舒适快捷地出行。因此,本文将80%作为乘客是否接受引导的阈值。
3.2 仿真环境搭建
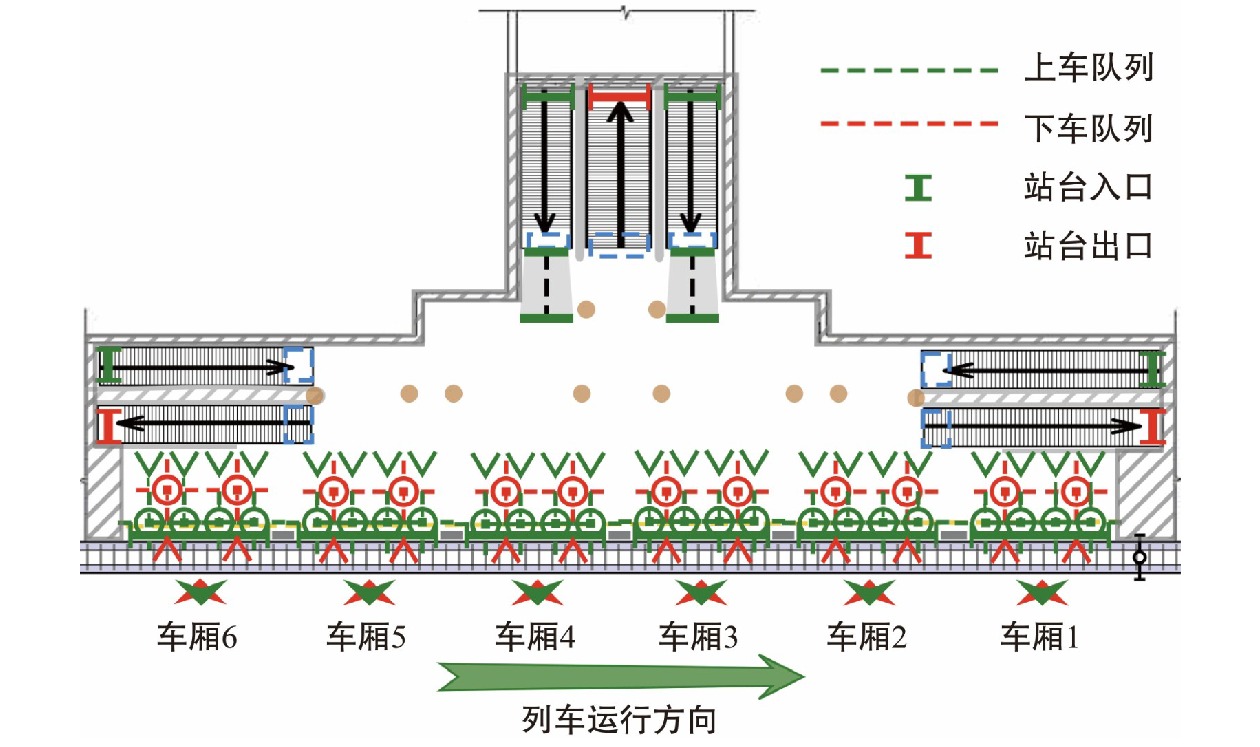
本仿真模型以广州地铁珠江新城站的5号线站台为原型,选用B6型列车[13]。珠江新城站为广州地铁车站2019年客流排名第2的车站,具有一定代表性,具体设施布局如图1所示。
3.3 仿真流线分析
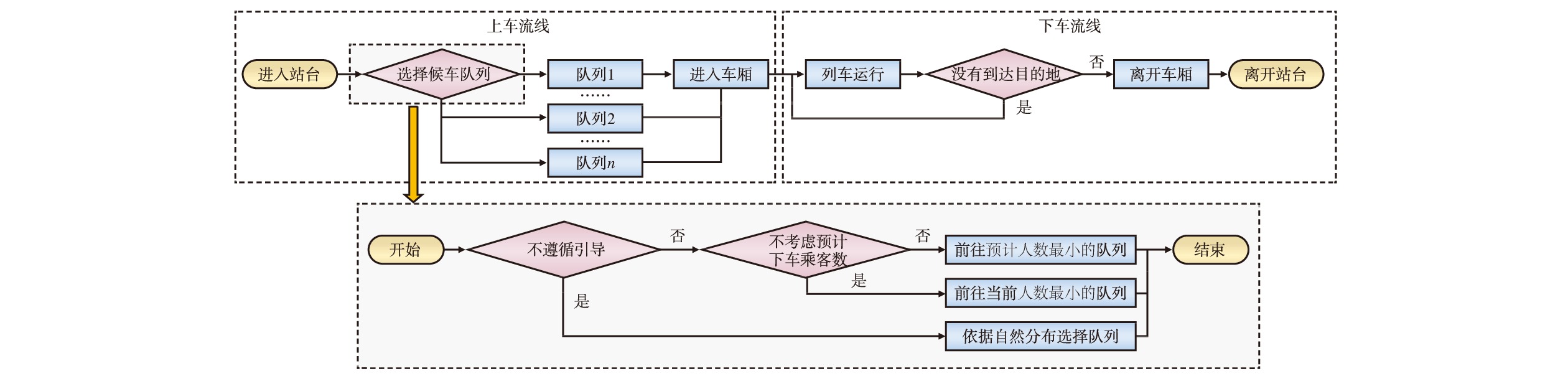
乘客在地铁车站内行动流线构成客流流线,主要分为上车流线和下车流线。上车流线指乘客到达站台层后,在选择候车队列上车这一系列行为而产生的流动路线;下车流线指乘客乘坐地铁到达目的地后,离开列车出站的路线。具体判断流程如图2所示。
乘客进入站台后,根据其是否遵循相关引导措施,划分为依据自然分布选择候车队列的乘客与接受引导的乘客。其中,接受引导的乘客又根据引导系统是否将预计下车乘客数纳入引导判断指标,从而通过不同的选择策略进行候车。本文为验证各节车厢下车人数这一影响因素对乘客分布不均衡度的影响,因此重点在于上车流线中选择候车队列这一判断阶段。
3.4 仿真模型构建
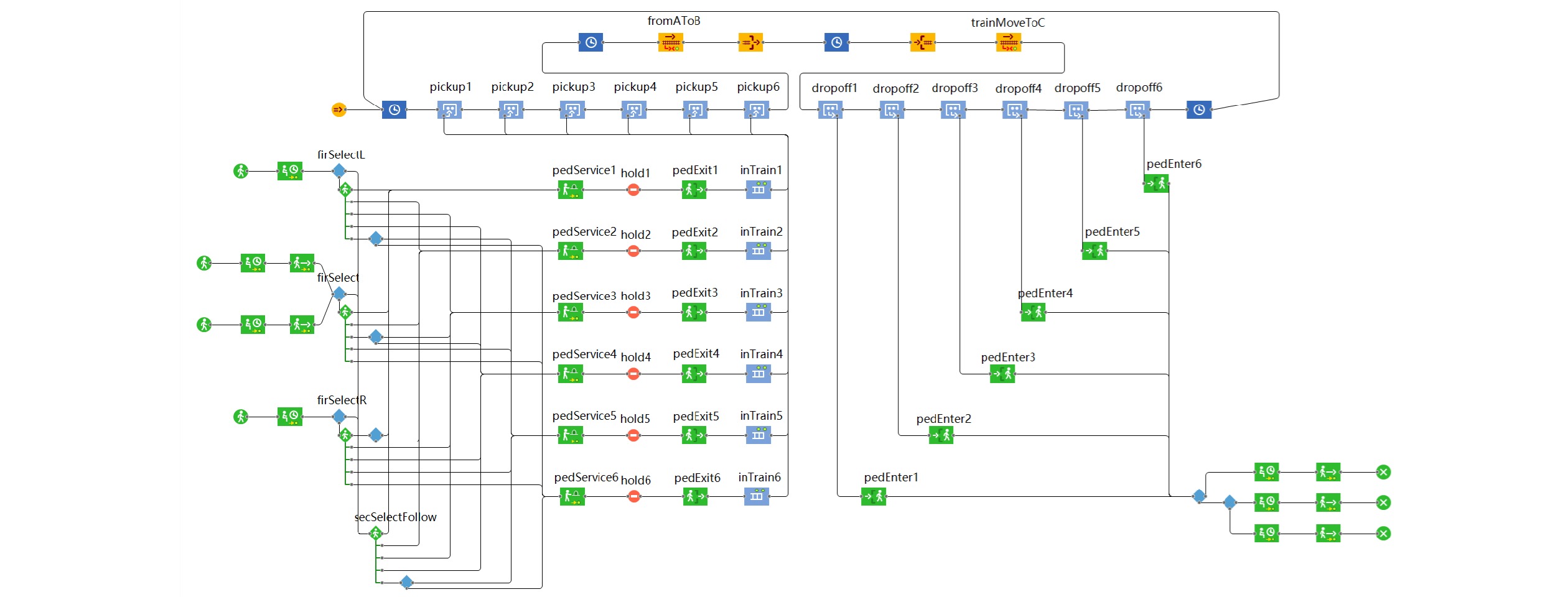
基于地铁站台运作流程的基本逻辑,本仿真模型综合运用了AnyLogic中的行人库、轨道库和流程库,如图3所示。
黄色模块为地铁运行流程图,利用AnyLogic轨道库建立列车轨道,通过空间标记标定关键元素(如停靠站台位置、轨道尽头跳转处等),以模拟地铁在多个站台减速入站、上下乘客、加速出站的运行过程。绿色模块为乘客乘车流程图,利用AnyLogic行人库构建了模型,标记了入站口、候车区、出站口等关键区域,以及乘客上车路线和排队队列。两个模块间通过AnyLogic流程库进行连接(即图中的蓝色模块),连接轨道库中的各车厢和行人库中上下车乘客之间的关系,并提供判断逻辑接口,以使预设的选择逻辑得以正常实现。
4 实验与分析
4.1 模型参数设置
通过对广州地铁5号线(滘口—文冲)全程POV(Point Of View)逐帧统计,将列车单站运行时间设置为80.53 s,乘客上下车时间设置为42.02 s,乘客离座预下车时间设置为45.53 s,地铁到站预开门时间及离站预加速时间均设为1 s,单个乘客上车耗时0.1 s。据文献[14],珠江新城5号线上车乘客中换乘乘客的比例为73.8%,下车乘客中换乘的比例为47%,详细设置参数如表1所示。
表 1 AnyLogic模型的相关参数设置模块 参数名称 参数值 TrainSouce 新车厢 carindex==0?new RailCar():carindex%2==0?new PassengerCar2():new PassengerCar1() 车厢长度 carindex==0?21:19 巡航速度 150/35(m/s) Delay 开门等候时间 42.02 s TrainMoveTo 巡航速度 200/45.53(km/h) Dropoff 下车比例 triangular(0, 1, 0.7) Pedsource(S) 到达速率 All*0.132 Pedsource(M) 到达速率 All*0.369 Pedsource(All) 舒适速度 uniform(0.5, 1) 初始速度 uniform(0.3, 0.7) 直径 uniform(0.2, 0.3) PedEnter 舒适速度 uniform(0.7, 1.2) 初始速度 uniform(0.5, 0.9) 直径 uniform(0.1, 0.2) secSelectUnfollow 动态值1 self.TYPE_PROBABILITIES(0.1, 0.1, 0.1, 0.1, 0.3,0.3) 动态值2 self.TYPE_PROBABILITIES(0.1, 0.1, 0.3, 0.3, 0.1,0.1) 动态值3 self.TYPE_PROBABILITIES(0.3, 0.3, 0.1, 0.1, 0.1,0.1) SelectOutput 乘客选择由站台中部通道离开概率(M) 0.47 乘客选择由站台两侧通道离开概率(S) 0.265 4.2 仿真模型运行原始数据
根据文献资料[12],珠江新城5号线日均客流量为24万人,设置客流量为12、24、36、48、60(单位:万人/日),对本文提到的3种引导方式分别进行模拟运行,每一条件下均衡度标准差的可信度均超过90%(1–α,α为均值置信),结果如表2、表3和表4所示。
表 2 采用引导方式1时乘客分布不均衡状况客流量/
(万人/日)计数/次 均衡度标准差 偏差 均值置信 总客流量/
人次12 147674 24.574 8.143 0.042 3628992.526 24 199761 48.433 15.824 0.069 9674977.691 36 210348 72.225 23.866 0.100 15192431.946 48 - - - - - 60 - - - - - 表 3 采用引导方式2时乘客分布不均衡状况客流量/
(万人/日)计数/次 均衡度标准差 偏差 均值置信 总客流量/
人次12 40491 15.442 4.813 0.047 625260.697 24 134002 30.223 9.240 0.049 4049875.470 36 73084 42.361 12.963 0.094 3095923.827 48 111060 50.647 16.528 0.097 5624844.113 60 182196 64.214 21.855 0.100 11699623.509 表 4 采用引导方式3时乘客分布不均衡状况客流量/
(万人/日)计数/次 均衡度标准差 偏差 均值置信 总客流量/
人次12 35141 11.519 4.409 0.046 404773.036 24 113375 22.488 8.567 0.050 2549572.184 36 68578 33.950 12.802 0.096 2328243.152 48 97391 43.842 15.812 0.099 4269783.179 60 180316 61.658 20.711 0.099 11117996.994 表2显示了在引导方式1的条件下,客流量从12万人/日至36万人/日时所对应的均衡度标准差。由于当客流量超过36万人/日时,站台会发生客流堆积现象,AnyLogic模拟平台无法在稳定情况下采样足够的数据,因此,统计缺少客流量为48万人/日和60万人/日时的相关数据。
表3显示了在引导方式2的条件下,客流量从12万人/日至60万人/日时的均衡度标准差。随着站台客流量的增加,采用了引导方式2的站台的乘客分布不均衡度也有着一定程度上升,且在相同客流量条件下,获得可靠性超越90%的均衡度标准差的采样次数相比引导方式1减少了许多,站台整体的乘客分布更加均衡稳定。
表4显示了在引导方式3的条件下,不同客流量时所对应的均衡度标准差。相比于引导方式2,引导方式3获得可靠性超越90%的均衡度标准差所需要的采样次数更少、站台整体的乘客分布更加均衡稳定。
4.3 仿真数据分析
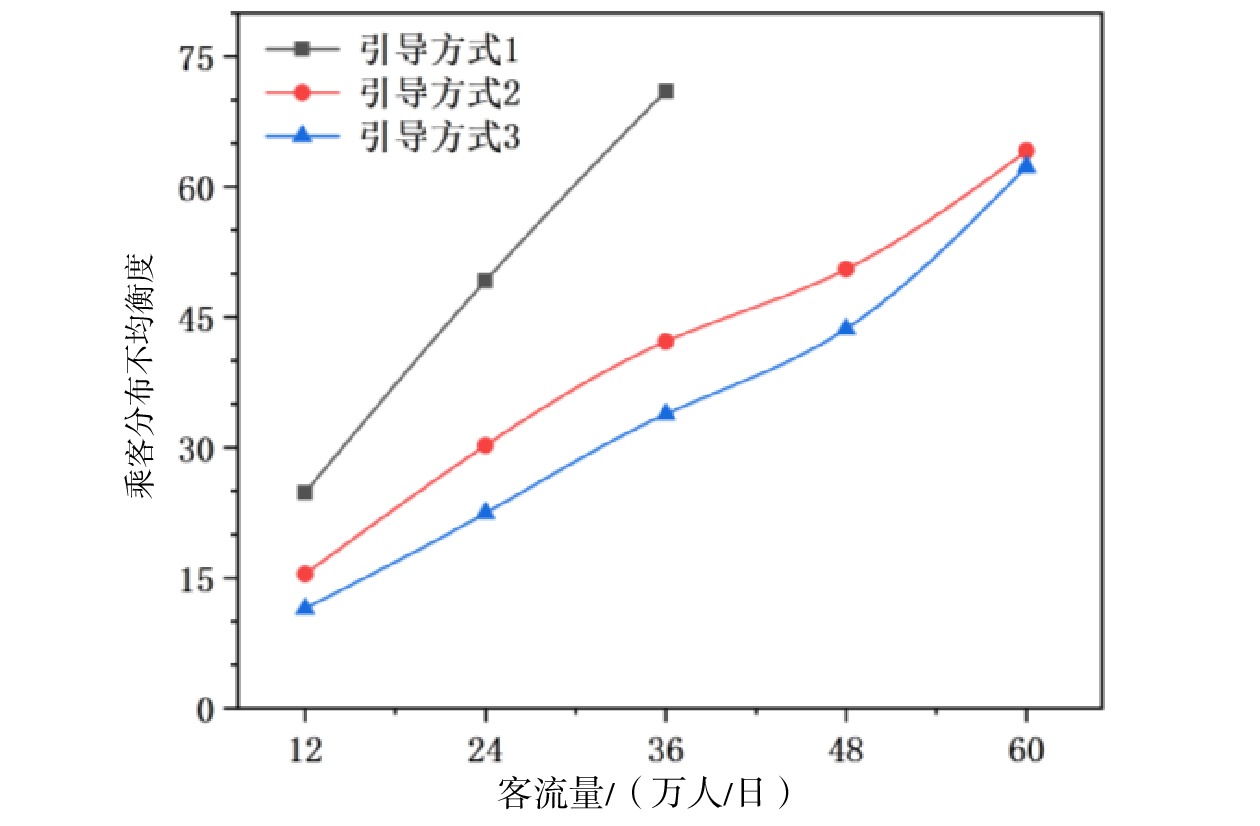
将获得的3种地铁站台客流引导方式下的均衡度标准差进行对比。相比于引导方式1仅能获得客流量在36万人/日以内的数据,引导方式2和引导方式3不仅能够顺利的获取客流量达60万人/日以内的数据,且客流分布不均衡问题也有了明显的改善。绘制折线图以更直观表示3种引导方式下乘客分布不均衡度随着客流量变化的情况,如图4所示。
通过观察可以发现:由于存在一定比例不愿遵循引导的乘客,因此随着站台流量的增大,各车厢乘客分布的不均衡程度均呈现出熵增状态。同时,引导方式3相对于引导方式2对客流分布不均衡的问题有了进一步的改善,但随着客流量的继续增大,由于站台输送能力的不足,改善效果有所减弱,各方式的引导效果趋近一致,此时需要采取限流等其他措施。具体的提升幅度如表5所示。
表 5 相对已有引导方式提升幅度客流量/
(万人/日)引导方式1
均衡度标准差引导方式2
均衡度标准差引导方式3
均衡度标准差方式3相对方式1的提升幅度 方式3相对方式2的提升幅度 12 24.574 15.442 11.519 53.1% 25.4% 24 48.433 30.223 22.488 53.6% 25.6% 36 71.023 42.361 33.950 52.2% 19.9% 48 - 50.502 43.672 - 13.5% 60 - 64.135 62.323 - 2.8% 当客流量到达珠江新城站5号线日均客流量24万人/日时,引导方式3相对引导方式2的提升幅度达25.7%,相比引导方式1的提升幅度达54.4%;随着客流量的增加,当客流量到达60万人/日时,引导方式3相对引导方式2的提升幅度逐渐降至2.8%。采用引导方式3,可以有效缓解平峰时段地铁客流分布不均衡的现象,提高了地铁站台客流引导系统精度,更有效地运用整列列车的容量。
4.4 仿真站台客流分布分析
乘客密度图可以更直观形象地显示站台乘客的分布。为使不同引导方式下站台客流分布的状况更加直观,将关键密度设置为9人/m2,观察仿真模型在AnyLogic软件虚拟时间模式下运行1 h的乘客密度图,如图5和图6所示。
由图5可知,在珠江新城站5号线的日均客流为24万人/日的压力下,引导方式1中部车厢的候车队列出现了小幅度的乘客集中现象,引导方式2和引导方式3的乘客分布均呈现均衡分布的状态。
由图6可知,在48万人/日的客流量压力下,引导方式1中部车厢的候车队列出现了明显的乘客堆积;对比引导方式2,引导方式3的站台堆积乘客数更少,乘客分布更加均匀。
5 结束语
本文在总结地铁站台现行的2种客流引导方式基础上,提出了一种新的引导思路,即在原有的车厢拥挤度和站台各车厢候车人数这2项引导指标下,加入各车厢预计下车人数这一影响因素,以更好地缓解地铁乘客分布不均衡现象。本文采用AnyLogic仿真软件,对不同客流条件3种引导方式下的乘客分布不均衡现象进行了研究,验证新思路的有效性。可以得出以下结论。
(1)在实际日均客流量的客流强度下,采用优化后的引导方式可显著缓解乘客分布不均衡现象,更有效地运用整列列车的容量。
(2)当客流量持续升高,甚至接近高峰小时客流量时,由于站台输送能力的不足,各方式的引导效果趋近一致,此时需要采取其他引导限流措施,配合其他公共交通方式,完成客流的输送。
文中仅针对侧式站台这一站台布局形式进行了仿真研究,截取了客流量在12万/日~60万人/日这一范围进行了统计分析。同时,文中也仅针对了车厢拥挤度、候车队列长度、预计下车人数等3方面因素对乘客候车的影响。在后续的研究中,将针对不同形式的站台、不同的客流强度,探讨对乘客分布不均衡度的影响,并将采用新型引导方式的客流引导系统用于实际地铁客流组织中进行验证。
-
表 1 AnyLogic模型的相关参数设置
模块 参数名称 参数值 TrainSouce 新车厢 carindex==0?new RailCar():carindex%2==0?new PassengerCar2():new PassengerCar1() 车厢长度 carindex==0?21:19 巡航速度 150/35(m/s) Delay 开门等候时间 42.02 s TrainMoveTo 巡航速度 200/45.53(km/h) Dropoff 下车比例 triangular(0, 1, 0.7) Pedsource(S) 到达速率 All*0.132 Pedsource(M) 到达速率 All*0.369 Pedsource(All) 舒适速度 uniform(0.5, 1) 初始速度 uniform(0.3, 0.7) 直径 uniform(0.2, 0.3) PedEnter 舒适速度 uniform(0.7, 1.2) 初始速度 uniform(0.5, 0.9) 直径 uniform(0.1, 0.2) secSelectUnfollow 动态值1 self.TYPE_PROBABILITIES(0.1, 0.1, 0.1, 0.1, 0.3,0.3) 动态值2 self.TYPE_PROBABILITIES(0.1, 0.1, 0.3, 0.3, 0.1,0.1) 动态值3 self.TYPE_PROBABILITIES(0.3, 0.3, 0.1, 0.1, 0.1,0.1) SelectOutput 乘客选择由站台中部通道离开概率(M) 0.47 乘客选择由站台两侧通道离开概率(S) 0.265 表 2 采用引导方式1时乘客分布不均衡状况
客流量/
(万人/日)计数/次 均衡度标准差 偏差 均值置信 总客流量/
人次12 147674 24.574 8.143 0.042 3628992.526 24 199761 48.433 15.824 0.069 9674977.691 36 210348 72.225 23.866 0.100 15192431.946 48 - - - - - 60 - - - - - 表 3 采用引导方式2时乘客分布不均衡状况
客流量/
(万人/日)计数/次 均衡度标准差 偏差 均值置信 总客流量/
人次12 40491 15.442 4.813 0.047 625260.697 24 134002 30.223 9.240 0.049 4049875.470 36 73084 42.361 12.963 0.094 3095923.827 48 111060 50.647 16.528 0.097 5624844.113 60 182196 64.214 21.855 0.100 11699623.509 表 4 采用引导方式3时乘客分布不均衡状况
客流量/
(万人/日)计数/次 均衡度标准差 偏差 均值置信 总客流量/
人次12 35141 11.519 4.409 0.046 404773.036 24 113375 22.488 8.567 0.050 2549572.184 36 68578 33.950 12.802 0.096 2328243.152 48 97391 43.842 15.812 0.099 4269783.179 60 180316 61.658 20.711 0.099 11117996.994 表 5 相对已有引导方式提升幅度
客流量/
(万人/日)引导方式1
均衡度标准差引导方式2
均衡度标准差引导方式3
均衡度标准差方式3相对方式1的提升幅度 方式3相对方式2的提升幅度 12 24.574 15.442 11.519 53.1% 25.4% 24 48.433 30.223 22.488 53.6% 25.6% 36 71.023 42.361 33.950 52.2% 19.9% 48 - 50.502 43.672 - 13.5% 60 - 64.135 62.323 - 2.8% -
[1] 广州地铁. 2017,2018,2019,2020,2021,2022年年报[EB/OL] 2023-06-28]. https://www.gzmtr.com/ygwm/gsgk/qynb/.
[2] 田洪金,殷 玲. 一种地铁站台门乘客引导系统的设计与实现[J]. 物联网技术,2022,12(5):75-76,79. [3] 王世轶,祁 勇,潘永剑,等. 一种地铁车厢拥挤度智能监测系统的研究[J]. 电子设计工程,2022,30(17):55-59. [4] 庞梦圆,杜彦君,厉超吉,等. 基于图像采集技术的地铁站台客流引导系统研究[J]. 都市快轨交通,2017,30(2):37-41. [5] Çapalar J, Nemec A, Zahradnik C, et al. Optimization of passenger distribution at metro stations through a guidance system[C]//Proceedings of the 16th International Conference on Computer Aided Systems Theory, 19-24 February, 2017, Las Palmas de Gran Canaria, Spain. Cham: Springer, 2018. 397-404.
[6] Ding H, Di Y R, Zheng X Y, et al. Passenger arrival distribution model and riding guidance on an urban rail transit platform[J]. Physica A:Statistical Mechanics and its Applications, 2021, 571(2): 125847. DOI: 10.1016/j.physa.2021.125847
[7] Zheng Z X, Wang H, Liu W M, et al. Toward real-time congestion measurement of passenger flow on platform screen doors based on surveillance videos analysis[J]. Physica A: Statistical Mechanics and its Applications, 2023, 612(4): 128474. DOI: 10.1016/j.physa.2023.128474
[8] 深圳地铁试点推出车厢拥挤度智能显示系统[J]. 都市快轨交通,2019,32(3):18. [9] 沙永杰,纪 雁,陈婉婷. 新加坡公共交通规划与管理[J]. 国际城市规划,2021,36(1):142-147. [10] 方晨晨,周继彪,董 升,等. 基于BP神经网络的地铁车厢拥挤度预测方法[J]. 交通信息与安全,2018,36(6):47-53. [11] 徐玉萍,江睿智. 交通运输效率、交通结构与经济发展[J]. 企业经济,2021,40(5):142-150. [12] 刘光通,孔德文,姚丽亚,等. 基于Wi-Fi嗅探技术的站台引导员效用及布置研究[J]. 交通信息与安全,2020,38(1):84-91. [13] 广州地铁官方网站. 广州地铁-列车介绍[EB/OL]. (2022-12-31)[2023-06-28]. https://cs.gzmtr.com/ckfw/lcjs_2020/. [14] 莫俊泓,石红国. 基于仿真的珠江新城站改造前后客流组织分析[J]. 综合运输,2021,43(12):119-126. -
期刊类型引用(1)
1. 高艺瑄,张锦月,王梓萱,李莹璇,沙峻林. 基于AnyLogic的龙王塘地铁站仿真分析. 人民公交. 2024(16): 116-118 .  百度学术
百度学术
其他类型引用(1)




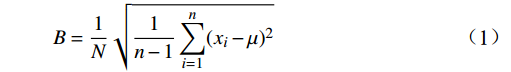
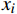
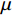

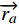
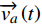

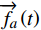
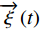
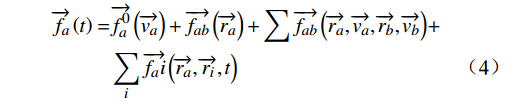
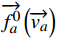
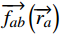
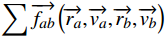
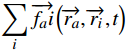
 下载:
下载: