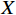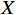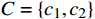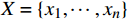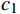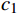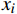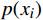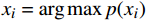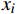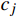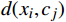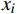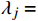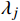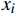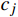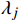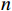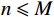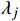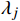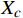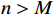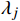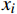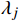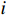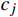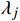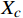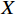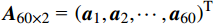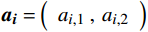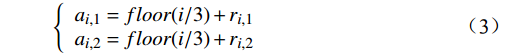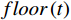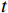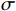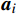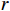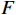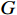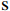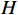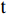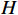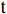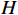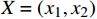KMeans based auxiliary design software for railway electrical equipment layout
-
摘要: 为解决铁路电务设备布放设计带来的聚类问题,基于KMeans算法,提出了BiKMeans_SC算法,实现了聚类数未知且带有规模限制的自动聚类,通过仿真实验证明该算法的可用性。基于BiKMeans_SC算法开发了铁路电务设备布放辅助设计软件,根据平面位置完成对电务设备的聚类处理,利用A*算法完成电务设备线缆的路径自动规划,实现了电务设备线缆连接图和线缆工程量的自动生成。实验证明,相对于传统的手动设计手段,该软件自动化水平高,计算过程有可靠依据且结果精确,有利于提高铁路电务设备布放的设计质量,控制建设投资成本,更好地服务铁路工程建设。Abstract: To solve the clustering problem caused by the layout design of railway electrical equipment, this paper proposed the BiKMeans_SC algorithm based on the KMeans algorithm, implemented automatic clustering with unknown number of clusters and size constraints, and its usability was demonstrated through simulation experiments. Based on the BiKMeans_ SC algorithm, the paper developed an auxiliary design software for railway electrical equipment layout, which implemented clustering processing of electrical equipment based on plane positions, used the A* algorithm to automatically plan the path of electrical equipment cables, realize the automatic generation of electrical equipment cable connection diagrams and cable engineering quantities. Experimental results have shown that compared to traditional manual design methods, this software has a high level of automation, reliable calculation processes, and accurate results, which is conducive to improving the design quality of railway electrical equipment layout, controlling construction investment costs, and better serving railway engineering construction.
-
在设计阶段通过科学手段提高设计精度,从源头合理规划工程方案,对于提高工程质量、节约建设投资、降低运营成本、推动铁路高质量发展具有重要意义[1]。在电务设备(简称:设备)布放设计过程中,设计人员需要在图纸中布放设备,再布放连接设备与机房设备间的线缆,满足设备的供电、通信和连通需求,形成可行的技术方案,最后绘制设备连接系统图并编制工程量表。传统的设计方法需要设计人员手动布置设备,人为确认线缆路径,统计线缆的工程量,效率低且易出错。
当前,BFS(Breadth First Search)算法、Dijkstra算法和A*算法等路径规划算法可实现线缆路径的自动规划及工程量计算[2-3]。但其主要针对点对点连接的场景,无法满足多设备复杂连接场景的需求。在铁路设备布放设计过程中,存在将终端设备分组,共用一路电缆供电的场景,此时设计人员需要对设备进行聚类处理,以组为单位进行线缆路径规划。传统的手动聚类方式效率低,难以得到最优方案。考虑到电缆的载流量标准,亟需研究适合铁路设备布放的聚类算法,基于设备位置数据实现自动聚类,并对聚类结果中每个簇的规模进行限制。
KMeans是一种常用的无监督聚类算法。该算法通过指定聚类数K,可根据输入数据间的相似度,自动将数据划分为K个簇,并得到每个簇的簇心。KMeans算法实现简单,适合输入数据没有标记且预先没有确定结果的情形,可用于根据设备位置坐标将设备分组。但其在应用过程中存在初始簇心随机选取导致聚类结果易陷入最优局部解等问题。由此,诞生了KMeans++和BiKmeans等改进算法[4-5],其可在一定程度上避免算法陷入局部最优解。为确定最佳聚类数,文献[6]采用手肘法,计算不同K值时的SSE(Sum of Squares due to Error)指标并绘制分布折线图,选择折线拐点对应的K值作为最佳聚类数;文献[7]提出基于加权二分图的算法,通过定义评价数L,计算不同K值下的L值来确定最佳聚类值。上述方法可在一定程度上得到最佳聚类数,但需要计算不同K值时的聚类结果,步骤繁琐且自动化程度低。针对KMeans算法无法限制聚类结果规模的问题,文献[8]提出的改进算法在将样本分配到每个簇前,先检查簇的规模,保证每个簇的样本总数不超过最大值,但依然需要事先指定聚类数;文献[9]使用了基于正交分解的收缩聚类算法,通过迭代处理可在聚类数未知时,实现带有最小规模限制的自动聚类,但无法限制最大规模。
综上所述,目前相关聚类算法的研究均无法较好地满足铁路设备布放设计的需求,而不同的分组结果导致配电设施设置、线缆敷设的数量有较大差异,直接影响工程投资。因此,将设备根据空间位置等特征进行聚类处理,进而依据聚类结果自动进行线缆路径规划,是研发设备布放辅助设计软件中需要深入研究的问题。
1 铁路设备布放聚类算法研究
1.1 BiKMeans_SC算法概述
Kmeans++算法通过计算每个样本被选为初始簇心的概率,实现对簇心的科学选择;BiKMeans算法通过对每次迭代过程中SSE较大的簇进行二分处理,在一定程度上避免了直接随机初始化K个簇心给聚类结果带来的影响。在上述算法基础上,本文结合铁路设备布放设计的特殊聚类需求,提出了BiKMeans_SC算法,通过给定规模限制最大值M和重复次数p,可自动完成对输入数据集
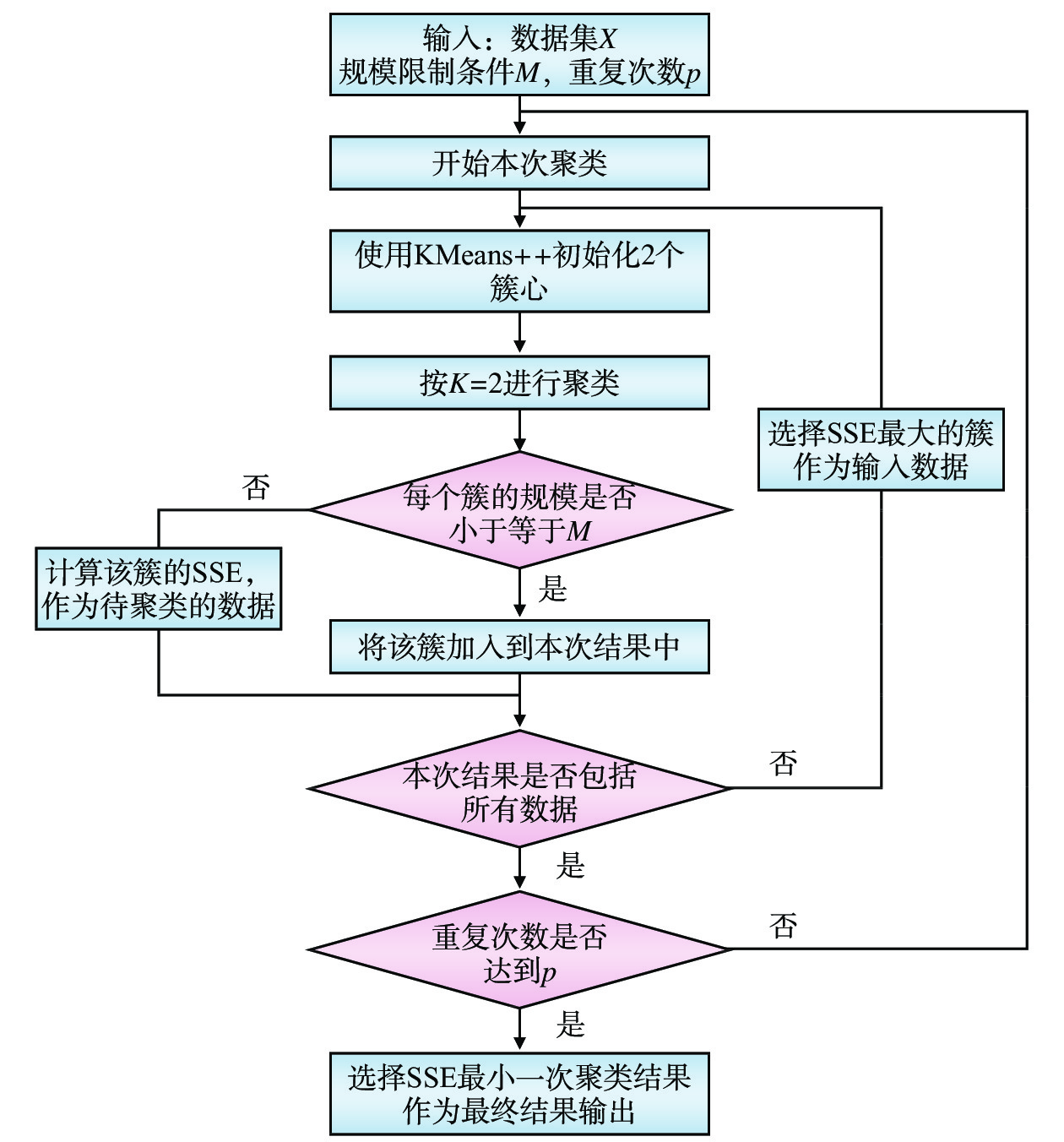
X={x1,⋯,xn} 的聚类处理,算法流程如图1所示。(1)给定输入值:待聚类数据集X、聚类结果的最大规模限制M和重复次数p。
(2)初始化空集合
Xc ,用来存储X 中已经完成聚类的样本。(3)对于待聚类数据集
X ,使用KMeans++方法初始化2个簇心C={c1,c2} ,具体方法为:①随机选中数据集
X={x1,⋯,xn} 中的某个样本作为第一个簇心c1 ;②逐个计算各样本
xi 距c1 的欧式距离di,1;③计算
xi 的被选中为簇心的概率p(xi) p(xi)=di,j/n∑i=1di,j (1) ④选择
xi=argmax 作为簇心c2,加入到C 中。(4)对
X 使用KMeans法进行聚类,具体方法为:①分别计算
X 中每个样本{x_i} 至每个簇心{c_j} 的欧式距离d({x_i},{c_j}) ,j=1,2,标记{x_i} 隶属簇{\lambda _j} = \arg \min d({x_i},{c_j}) ;②基于
{\lambda _j} 的每个样本{x_i} ,求取它们的平均值作为簇心{c_j} 的新值;③重复①~②,直至全部簇心不再变化。
(5)判断每个簇
{\lambda _j} 中样本总数n ,若如n \leqslant M ,则{\lambda _j} 满足规模限制,将{\lambda _j} 中的每个样本添加到{X_c} 中;若n > M ,则计算簇{\lambda _j} 的SSE指标SSE = \sum\limits_{i = 1}^n {{{({x_i} - {c_j})}^2}} (2) 式中,
{x_i} 为{\lambda _j} 中的第i 个样本;{c_j} 为{\lambda _j} 的簇心。选择SSE指标最大的簇作为待聚类数据集,重复步骤(3),直至{X_c} 包括X 的所有元素。(6)重复步骤(2)~(5)达到p次,则计算每次聚类结果所有簇的SSE指标之和,选择值最小一次的聚类结果作为最终结果输出。
BiKMeans_SC算法使用了与BiKMeans同样的二分迭代方法,通过在每次迭代过程中检查每个簇的样本总数,将满足规模限制的簇提取出来,添加到聚类结果中,直至结果包含所有的输入数据。该算法无需事先指定聚类数,亦无需进行不同K值下聚类结果的计算,利用簇的规模限制条件实现了聚类数未知的情况下数据集的自动聚类。
BiKMeans_SC算法参考KMeans++完成初始簇心的选取,并设置了重复次数p,对数据集多次处理,以每次聚类结果的SSE为指标,选择最小的一次作为最终结果,最大程度避免了算法的随机性。
1.2 仿真验证
给定一个二维矩阵
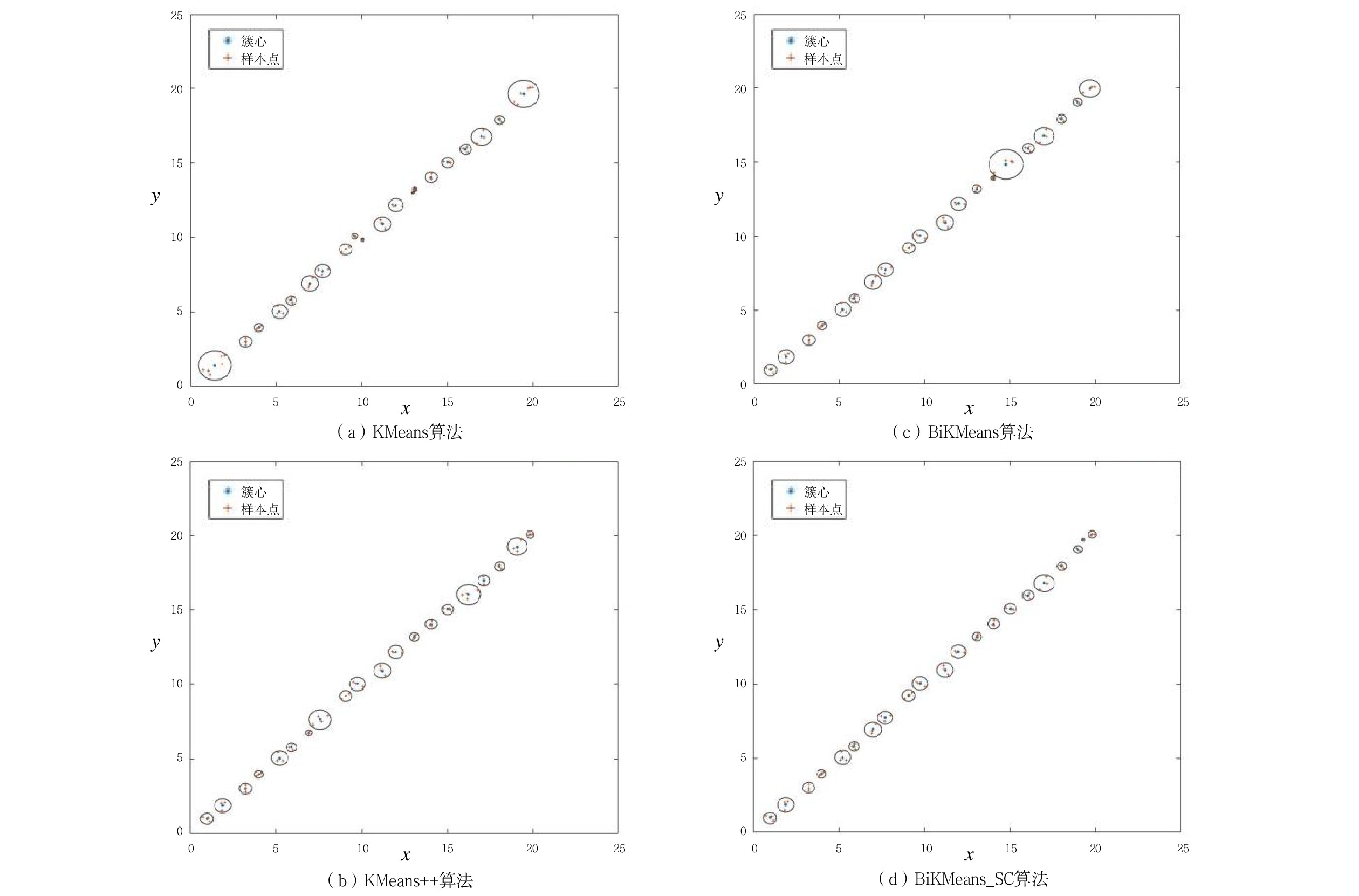
\boldsymbol{A}_{60\times2}\text{ = }\left({\boldsymbol{a}}_1,{\boldsymbol{a}}_2,\cdots,{\boldsymbol{a}}_{60}\right)^{\mathrm{T}} 作为输入数据集进行聚类处理,{{{{\boldsymbol{a}}_{\boldsymbol{i}}}}} = \left( {\begin{array}{*{20}{c}} {{a_{i,1}}} \;,\;{{a_{i,2}}} \end{array}} \right) 是一个二维向量,代表A中第i行元素,i=1,2,···,60。其定义表达式为\left\{ {\begin{array}{*{20}{l}} {{a_{i,1}} = floor(i/3) + {r_{i,1}}} \\ {{a_{i,2}} = floor(i/3) + {r_{i,2}}} \end{array}} \right. (3) floor\left( t \right) 表示不超过变量t 的最大整数值,且是随机数,表示叠加在第i行输入数据上的噪声,\sigma 为0.2。分别使用KMeans、KMeans++、BiKMeans、BiKMeans_SC算法对矩阵A60×2进行聚类处理。其中,使用KMeans、KMeans++、BiKMeans算法时,设定聚类数为20,使用BiKMeans_SC算法时,设定M为3,p为10。以A60×2中第1列值作为x,第2列值作为y,不同算法得到的聚类结果及簇心分布如图2所示,图2中每个圆代表一个簇。由公式(3)可知,A中每行元素
\boldsymbol{a}_i 是行标i除以3的整数商,叠加上扰动噪声r 。A中共有60行,可知理想结果为,将A分为20个簇,每个簇中均含有3个样本,得到的各算法的聚类结果如表1所示。表 1 各算法聚类结果聚类算法 各类簇的数量统计 聚类数 SSE D1 D2 D3 D4 D5 D6 KMeans 2 2 14 0 0 2 20 7.4865 KMeans++ 0 2 16 2 0 0 20 3.7345 BiKMeans 0 2 16 2 0 0 20 4.4421 BiKMeans_SC 1 1 19 0 0 0 21 3.1293 表注:Di表示该簇的样本总数为i 由表1可知,在指定划分为20个簇的前提下,相对于经典KMeans算法,KMeans++、BiKMeans算法得到的簇的样本总数分布更贴近理想情况,SSE指标值更低,比KMeans算法聚类效果更优。BiKMeans_SC算法在没有预先指定聚类数的情况下,自动将数据集划分为21个簇,每个簇的样本总数均不超过3,接近理想情况,解决了聚类数未知时带有规模限制的聚类问题,且综合了KMeans++和BiKMeans算法的优势,得到了更小的SSE指标值。
2 辅助设计软件设计
2.1 数据集提取
设计人员通常在CAD图纸中布放设备、标注线缆,完成设计工作。设备在图纸中的位置坐标即为真实环境位置的等比例映射,设备间相对位置关系与实际关系一致。本文使用ObjectARX工具,提取所有待聚类设备在图纸中的平面坐标,形成一个二维数组。为方便数据处理及结果展示,需要对数据进行归一化处理,使所有设备坐标均处于[0,1]区间,将其作为输入数据集,同时,输入每个簇的规模最大值,基于BiKMeans_SC算法,实现K值未知条件下的设备聚类。
2.2 线缆路径规划
在进行路径规划时,常使用邻接矩阵表述路径图。基于给定的路径图,进行线缆路径规划时,常用的路径搜索算法有BFS、Dijkstra和A*算法。BFS是一种盲目搜寻算法,能找到最短路径但计算量较大;Dijkstra算法考虑了顶点间的移动距离,对比BFS算法能更快找到最短路径,但会计算起点至所有顶点的最短路径,造成计算资源的浪费;A*算法在Dijkstra算法基础上进行改进,通过定义启发函数,辅助进行路径选择,可比Dijkstra更快找到最短路径。本文使用优势最突出的A*算法进行线缆路径规划的实现。
A*算法中启发函数
F 的表达式为F = G + H (4) 式中,
G 为从起点\mathrm{s} 至某一指定顶点q的移动距离,由路径图给定;H 为从q到目标点\mathrm{t} 的估算距离,需自行确定。H 值必须小于从q到\mathrm{t} 间的实际距离,常用的H 计算公式有曼哈顿距离计算和欧式距离计算,以2个二维顶点X = ({x_1},{x_2}) 、Y = ({y_1},{y_2}) 为例:曼哈顿距离计算式为
H = \left| {{x_1} - {x_2}} \right| + \left| {{y_1} - {y_2}} \right| (5) 欧式距离计算式为
H = \sqrt {{{({x_1} - {x_2})}^2} + {{({y_1} - {y_2})}^2}} (6) 考虑到实际中线缆并不总是水平或垂直敷设的,使用曼哈顿距离公式计算得到的数值可能会超过两点间敷设线缆所需的实际长度,因此,本文选用欧式距离作为估算距离
H 的计算公式。以设备聚类结果中每个簇的中心点为终点,以机房配线间等为起点进行路径规划,并根据规范和实际情况,考虑线缆的余长预留。2.3 软件开发
本文基于C#语言在Visual Studio平台进行软件的开发[10],实现设备聚类及线缆路径规划,软件运行流程如图3所示。
3 实验验证
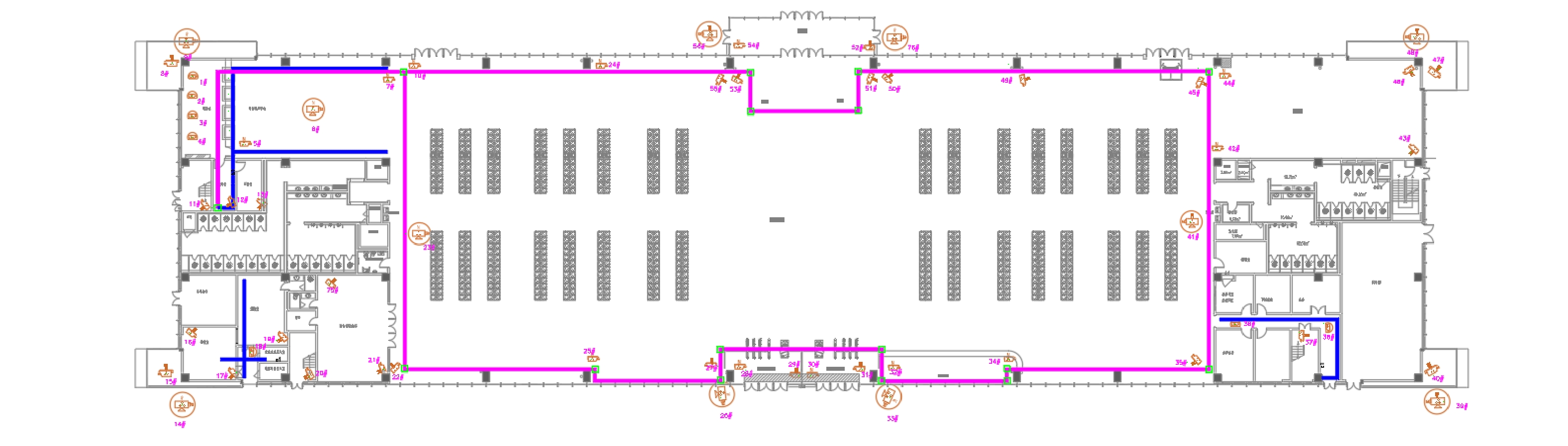
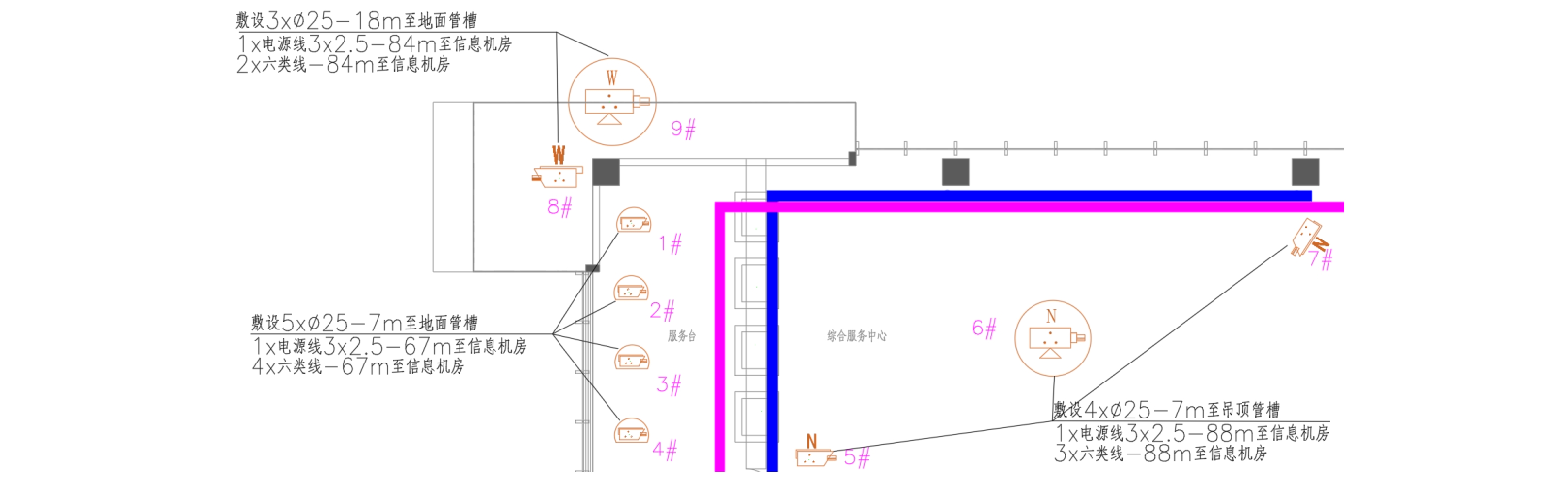
以某车站视频监控系统的设计过程为例,采用本文辅助设计软件,以摄像机的空间位置为测试数据进行聚类处理,并对摄像机电源线缆的路径进行自动规划。该车站的站房共2层,布置了73台不同类型的摄像机,站房首层建筑平面及摄像机的分布位置如图4所示,图4中的粉色及蓝色直线分别代表了地面和吊顶的线缆槽道。
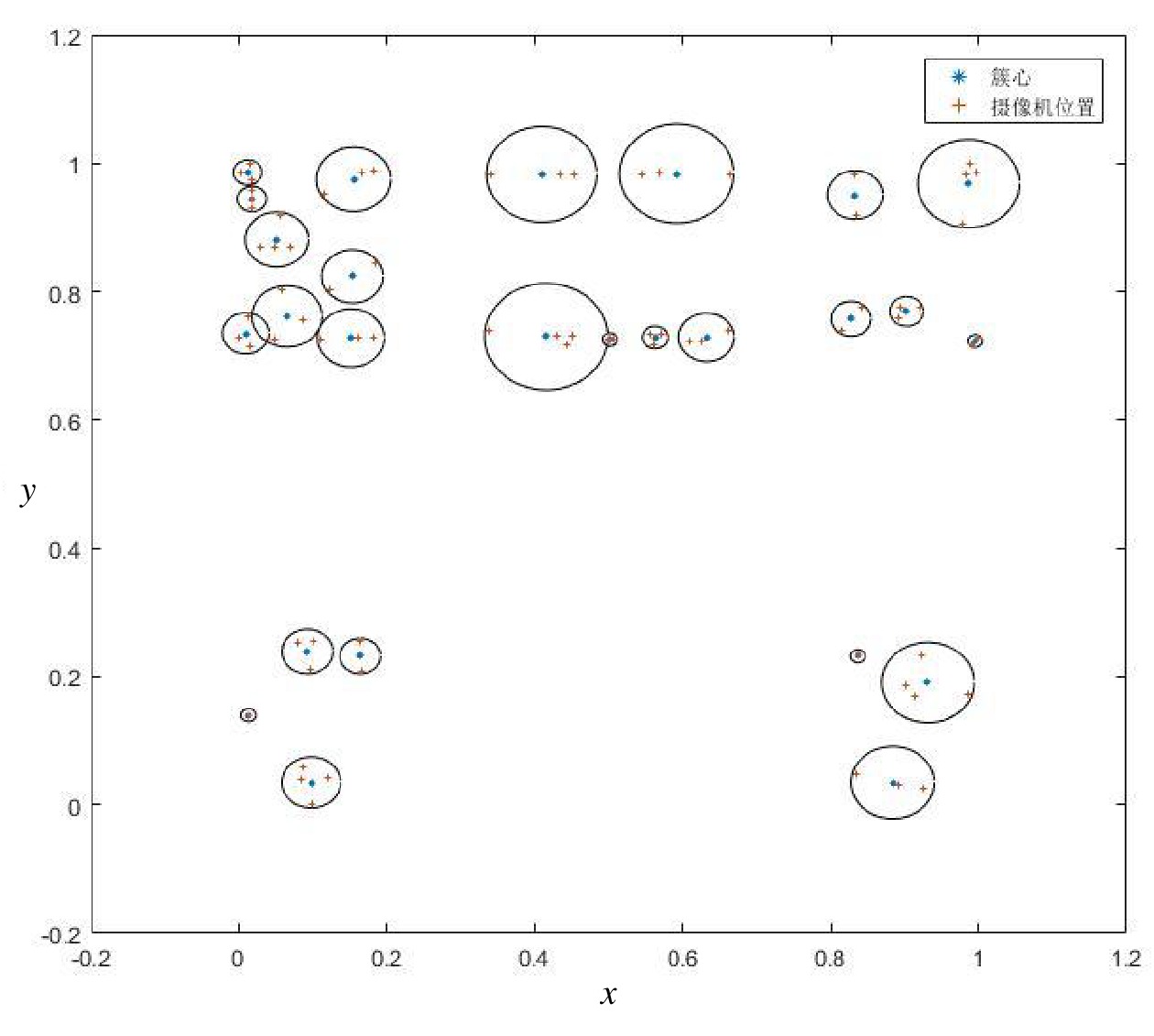
受电源线允许通过的最大电流限制,最多4台摄像机共用一路电源线。使用BiKMeans_SC算法对摄像机的空间位置进行聚类处理,将摄像机在图纸中的横纵坐标归一化,作为x、y值,该x、y值与聚类结果如图5所示,图5中每个圆圈代表一个簇。可看出BiKMeans_SC算法将73组测试数据分为26个簇,每个簇的样本总数均不超过4,实现了预期目标。
根据图5所示的摄像机分组结果,使用A*算法自动生成每组摄像机电源线缆的路径和长度,部分摄像机的线缆信息标注如图6所示。
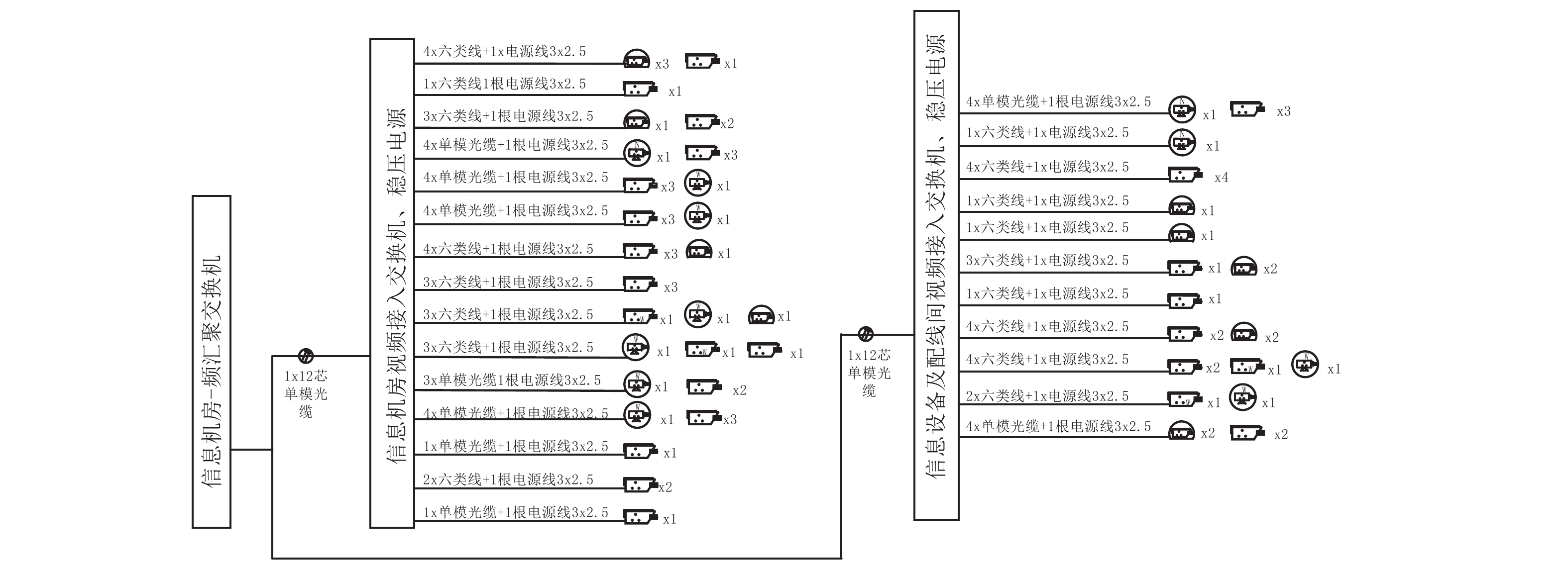
最终,辅助设计软件设计的电源线缆总长度为1996 m,相对于设计人员手工分组、手动测量得到的线缆长度2600 m,使用本辅助设计软件节省了23.2%的线缆。根据设备的分组信息和计算得到的线缆信息,软件能自动生成如图7所示的视频监控系统线缆连接示意图。
本文设计的辅助设计软件在铁路多个站房视频监控系统的设计阶段进行了测试,试验结果均证明该软件能有效减少设计人员的工作量,精准控制线缆工程量,提高施工图设计质量。
4 结束语
针对聚类数未知且带有最大规模限制的铁路电务设备布放聚类需求,本文设计了BiKMeans_SC算法对数据集进行聚类,通过仿真实验证明了该算法能切实完成聚类任务。利用BiKMeans_SC算法和A*算法开发辅助设计软件,实现了平面设备的自动分组、线缆路径的自动规划、设备与线缆连接图的生成。
相对于传统的手动设计方式,本文软件能自动生成精准科学的设备分组结果和线缆工程量,减少了设计人员的工作量,提高了设计质量和效率,节省了工程投资。本文设计的BiKMeans_SC算法具有通用性,对铁路站房设备分组、线路区间内的设备分组汇聚、区间房屋的选址等都有一定的辅助设计作用。
-
表 1 各算法聚类结果
聚类算法 各类簇的数量统计 聚类数 SSE D1 D2 D3 D4 D5 D6 KMeans 2 2 14 0 0 2 20 7.4865 KMeans++ 0 2 16 2 0 0 20 3.7345 BiKMeans 0 2 16 2 0 0 20 4.4421 BiKMeans_SC 1 1 19 0 0 0 21 3.1293 表注:Di表示该簇的样本总数为i -
[1] 刘振芳. 埋头苦干 勇毅前行 奋力推动铁路高质量发展 勇当服务和支撑中国式现代化建设的“火车头”——在中国国家铁路集团有限公司工作会议上的报告(摘要)[J]. 铁路计算机应用,2023,32(1):1-8. [2] 孙泽人. 基于重心选址法的建筑电气管线优化研究[D]. 北京:北京建筑大学,2020. [3] 杨 旭,周德俭,宋 微,等. 一种考虑复杂约束的线缆束路径规划方法[J]. 西安电子科技大学学报,2021,48(3):197-204. [4] 张玉琴,梁 莉,张建亮,等. 基于改进K-means++和DBSCAN的大数据聚类方法[J]. 国外电子测量技术,2022,41(9):40-46. [5] 马文博,巫朝霞. 基于差分隐私保护的二分k均值聚类算法研究[J]. 智能计算机与应用,2023,13(2):155-160,164. [6] 陶永辉,王 勇. 基于初始聚类中心选取的改进K-means算法[J]. 国外电子测量技术,2022,41(9):54-59. [7] 林伟杰,王 勇,周 林. 基于加权二分图的K均值最佳聚类数确定算法[J]. 计算机工程与设计,2023,44(4):1104-1111. [8] Ganganath N, Cheng C T, Tse C K. Data clustering with cluster size constraints using a modified K-means algorithm[C]//Proceedings of 2014 International Conference on Cyber-Enabled Distributed Computing and Knowledge Discovery, 13-15 October, 2014, Shanghai, China. New York, USA: IEEE, 2014.
[9] Hu C W, Li H Y, Qutub A A. Shrinkage clustering: a fast and size-constrained clustering algorithm for biomedical applications[J]. BMC Bioinformatics, 2018, 19(1): 19. DOI: 10.1186/s12859-018-2022-8
[10] 刘升法. 基于AutoCAD的铁路站房信息系统施工图辅助设计软件的研发[J]. 铁路计算机应用,2023,32(1):52-56. -
期刊类型引用(2)
1. 张炼. 面向复杂环境的自动规划辅助软件抗毁性优化研究. 九江学院学报(自然科学版). 2025(01): 88-92 .  百度学术
百度学术
2. 贾拴平. 铁路工务设备管理系统设计与应用. 中国高新科技. 2025(08): 97-99 .  百度学术
百度学术
其他类型引用(1)




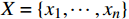
 下载:
下载: