Health status evaluation model for railway passenger station ticketing equipment based on data and model dual driven
-
摘要: 为及时掌握铁路客运车站(简称:客站)票务设备异常情况,评估其健康状态,采用数据驱动和模型驱动交互联动思想,提出了基于数模双驱动的票务设备健康状态评估模型。通过分析票务设备历史运行数据,构建以票务设备寿命预测值与实际值均方误差最小为核心的目标函数,利用优化算法求解其健康状态评价模型参数,实现对在役票务设备健康状态的评估。选取某铁路客站实名制核验闸机数据进行试验,结果表明,所提模型提高了客站票务设备健康状态评估的准确性,为客站票务设备精细化运行维护、预测性维修及主动运行维护提供了理论基础和决策依据。Abstract: In order to timely grasp the abnormal situation of ticketing equipment in railway passenger stations and evaluate their health status, this paper adopted the idea of data driven and model driven interactive linkage, and proposed a ticketing equipment health status evaluation model based on data and model dual driven. The paper analyzed the historical operating data of ticketing equipment, constructed an objective function with the minimum mean square error between the predicted and actual values of equipment life as the core, and used optimization algorithms to solve the parameters of the ticketing equipment health status evaluation model, implemented evaluation of the health status of in-service ticketing equipment and selected real name verification automatic fare gate data from a certain railway passenger station for testing. The results show that the proposed model improves the accuracy of the health status evaluation of the passenger station ticketing equipment, provides a theoretical basis and decision-making basis for the refined operation and maintenance, predictive maintenance, and active operation and maintenance of passenger station ticketing equipment.
-
财务共享中心是大型集团企业施行财务集中管控的重要手段,通过对企业内部重复度高、分散的财务工作进行集中化、规模化、标准化处理,为本企业各经营实体提供高效、准确、规范的财务共享服务,实现企业财务数据的集中管理与共享,提高财务工作效率,降低财务成本。2019年,中国国家铁路集团有限公司(简称:国铁集团)启动财务共享服务中心建设工作,并于2021年底先行在中国铁路太原局集团有限公司(简称:太原局)初步完成财务共享中心建设。截至2024年12月,18个铁路局集团公司均已完成财务共享中心建设,应用财务共享系统,将传统线下报销业务全部迁移至线上处理,通过深度整合线上审批流程,合并同一审批节点的大额联签、预算等审批事项,消除原先线下审批流程中的冗余环节,简化了审批流程,提高了审批效率。
作为铁路财务共享服务中心各项职能高效执行的信息化工具,财务共享系统是国铁集团数字化转型的核心抓手,旨在通过集中化、标准化和智能化手段提升财务管理效率,为铁路经营管理现代化提供支撑。不同于铁路财务会计管理信息系统下其它财务应用系统,财务共享系统面向铁路企业各层级经营实体单位,提供统一、规范的电子报账处理服务,系统用户除了财务共享服务中心各岗位人员,还包括铁路企业各层级经营实体的员工,报销业务处理在客观上与铁路企业各层级经营实体的既有业务信息系统存在着紧密的数据共享需求。然而,因财务共享系统与相关各业务系统尚未完全联通,对于同一经济事项,业务人员仍需分别在业务系统和财务共享系统中进行重复的数据维护和业务操作,不但加大了工作量,也无法保证不同系统间共用数据的质量。财务共享服务中心作为企业重要的财务数据中心,应当将企业财务数据挖掘和分析作为重点工作,而财务共享系统尚无数据分析功能,目前各项财务数据统计和分析主要还是由企业财务人员(简称:业财人员)在账表子系统内完成。为全面提升财务共享服务中心的信息化管理水平,亟需在财会共享系统既有功能的基础上,进一步完善对财务共享服务中心主要岗位各项业务的信息化支持。截至2024年底,国铁集团各级全资、控股和参股企业数量已达2 147家,各级企业业务性质千差万别,既有业务系统数量众多,这些业务系统与财务管理系统间信息共享程度低,打破信息壁垒是财务共享服务中心有效发挥财务集中管控职能的关键所在。
数据中台是一个集中化的数据管理平台,负责整合、处理和管理企业数据资产,提供标准化、可复用、高效、便捷、安全的数据服务,支撑前端业务应用,已被广泛应用于金融[1]、电力[2]、媒体[3]等领域。数据中台可将企业内外部全域海量、多元、异构数据进行集成整合,建立统一的数据存储和管理机制,形成标准化、口径统一的数据资产,通过抽象封装,向应用层面提供灵活、共享的数据服务,以满足各种管理应用场景下多样化数据使用需求,构建企业数据生产—消费—再生的闭环[4]。
本文围绕财务共享服务中心岗位及主要业务,在财会数据共享平台和铁路一体化信息集成平台尚不能提供财务及相关业务信息共享服务的条件下,针对当前迫切的信息共享需求,研究开发财务共享应用数据中台,以打破业财信息壁垒为目的,全面梳理财务共享系统和既有系统的数据共享需求,建立统一的数据标准,实现业财数据的自动采集,为铁路企业集团总部、铁路局集团公司、站段提供统一的公用数据维护入口,使财务共享系统与其它系统间能够便捷地共享数据,为财务共享系统应用功能的进一步完善和拓展提供有力数据支持。
1 财务共享系统应用现状及信息共享需求
1.1 铁路企业财务共享服务中心职责与主要业务
铁路企业财务共享服务中心依托财务共享系统,运用信息化手段和相关制度、流程管控措施,将分散在铁路企业的报账资料审核、凭证编制、资金支付以及报表编制等业务集中统一起来,以数据为中心,以流程为支撑,以服务为载体,实现财务资源的汇聚和集约高效,强化铁路企业管控力度,为铁路企业战略规划、经营决策、风险防控、业绩评价提供数据支持和报表分析,为铁路企业经营生产、运营管理、基础数据配置提供服务保障。
财务共享服务中心下设综合运营部、数据应用部、会计业务部、总账报表部及资金票据部等5个部门,各部门职能如表1所示。
表 1 铁路企业财务共享服务中心各部门主要职责部门 职能 综合
运营部负责综合事务、后勤保障、党建、群团等综合性工作;开展质量、绩效、培训、流程及风险监控等工作;处理员工报账咨询、投诉,定期进行用户回访和满意度调查等 数据
应用部负责系统主数据、审批流、标准等基础信息的配置及运维支持;与铁路企业开展合作,提供更加深入全面的经济活动分析等数据;出具标准化的管理类会计报表 会计
业务部负责铁路企业收入、收款、费用、税金、物资、资产等相关业务报账资料审核、会计核算等工作 总账
报表部负责一般总账业务的单据提报、审核、会计核算等全流程处理,以及银行账户日常对账、银行余额调节表编制及月度、季度、年度财务报表的编制工作 资金
票据部负责资金支付信息的审核及付款结算、收款流水分拣、票据管理等工作 其中,会计业务部、总账报表部、资金票据部岗位按审核内容、审核人员资质、审核重点及目的、审核流程先后顺序、风险控制侧重点等,细分为初审岗和复审岗。通过梳理、优化、再造铁路企业现有业务,财务共享服务中心最终形成费用报销、资金结算、物资、运输进款、收入、成本、资产、薪酬、税务、总账、财务报表编报、单据扫描及实物单据管理、会计档案管理13个一级流程,201个末级流程。只有不断扩展和完善财务共享系统的功能,使之成为支撑财务共享服务中心运营的强有力工具,才能准确、高效、安全地完成如此繁杂的业务处理。
1.2 财务共享系统应用现状及存在问题分析
1.2.1 财务共享系统简介
2019年,按照“统一领导、统一规划、统一标准、统一平台、统一管理”的原则,国铁集团财务部开始推进铁路管理信息化整合工作。在铁路一体化信息集成平台的基础上,建立财会数据共享平台,构建一个高度集成的综合性财会信息系统(统称:铁路财务会计管理信息系统),涵盖会计核算、财务预算、资金管理、收入管理、清算管理、成本管理、税务管理、财务监管、财务共享、会计人员管理 10 大主要应用。
目前,铁路企业财务实行集团总部、铁路局集团公司(国铁集团所属各专业公司)、站段(铁路局集团公司所属非运输企业和控股合资铁路公司)三级核算管理体制[5]。铁路财务会计管理信息系统部署在内部服务网,提供面向国铁集团、所属各单位、基层单位的三级联网应用。财务共享系统作为铁路财务会计管理信息系统重要组成部分,其主要功能包括电子报账、共享运营、电子档案和电子影像。财务共享系统已与账表子系统、资金结算子系统联通,可实现系统间凭证和支付信息的自动推送,以及科目、维度、电子回单的数据同步,如图1所示。
(1)电子报账:对收入、成本、费用、物资、资产、薪酬、税务等报账业务流程进行整合,通过报账单实现日常报账业务的高效处理,并实行精准的成本预算控制,是财务共享系统的基础。
(2)共享运营:实现财务业务统一处理的集成枢纽,作为财务共享服务中心开展日常作业的核心操作平台,是财务共享服务中心人员开展任务管理、凭证管理、支付管理、绩效管理、运营监控等各项运营管理工作的有效工具。
(3)电子影像:具备影像采集、影像调阅、影像任务处理、系统配置等功能,通过提供影像流,支持财务共享服务中心完成远程审核工作。
(4)电子档案:具备凭证管理、凭证分册、凭证借阅、档案管理等功能[6],完成电子凭证和电子报账资料的同步打印,方便电子会计凭证与报账资料的统一管理。
1.2.2 财务共享系统的报账流程
在财务共享系统的支持下,一笔报账业务从提单、报表数据生成到会计资料归档会经过一系列处理环节,如图2所示。
(1)供应商申请及信息维护:报账单提报前,报账人向本单位业财人员申请在账表子系统中增加供应商信息(供应商名称、纳税人识别号),由账表子系统运维人员将申请信息与企业信息查询工具(企查查、天眼查等互联网应用)查询到的信息进行比对,确认无误后完成供应商信息添加,并将供应商信息同步至财务共享系统;报账人在财务共享系统中提报“基础数据调整申请单”,对供应商银行账户信息(开户行名称、银行账号、联合行号)进行维护,完成报账单提报的基础准备工作。
(2)报账单提报:经济业务事项完成后,报账人在电子报账模块录入发票信息,根据不同业务填写相应的报账单,并与已录入的发票建立关联,发起报账流程,同时在线下将打印好的纸质报账单封面、发票、纸质附件资料等原始单据交由扫描岗。
(3)报账单扫描:扫描岗完成原始单据的核对、扫描后,将相关图像上传至电子影像模块,利用报账单封面上报账单号完成图像与报账单的自动匹配。
(4)合规性检查:财务共享系统内置了差旅费、会议费、业务招待费等费用报销项的标准控制规则及预算金额限制,报账人必须提报符合标准控制要求的报账单,且超出预算限制时无法提交报账单;通过在后台事先设置好的单据敏感词(如香烟、白酒、娱乐消费等),对报账人提报的原始单据进行校验,自动完成合规性检查。
(5)非资金支付类报账单审批及凭证生成:当电子影像模块完成影像与报账单的自动匹配后,电子报账模块按预先设置好的审批流程,自动发起报账处理,将报账单自动流转至各审批节点;当完成本企业内部的审批后,报账单将自动流转回财务共享服务中心;经财务共享服务中心初审岗、复审岗审核后,共享运营模块将预制凭证信息定时推送至账表子系统,并生成相应的转账凭证。
(6)资金支付类报账单审批及凭证生成:资金支付类报账单经财务共享服务中心初审岗、复审岗审核后,共享运营模块将支付信息推送至资金结算子系统;经资金结算子系统审批无误后,通过银企直联通道,将支付指令实时传递至开户银行;开户银行接收请求,完成风险控制与资金划转后,将支付完成信息返回资金结算子系统;共享运营模块接收资金结算子系统推送的支付完成信息后,自动将支付完成信息推送至账表子系统,并生成付款凭证。
(7)报表数据生成:依据共享运营模块定期推送过来的会计凭证信息,账表子系统利用会计科目取数公式,对已归集在本系统中的财务数据进行提取、整理、分析,生成铁路企业所需的各类财务报表,为企业决策提供财务数据支持。
(8)会计资料归档:电子影像模块接收账表子系统生成的凭证影像,通过报账单编号匹配原始单据和凭证影像,利用电子档案模块完成对电子会计资料的归档,同步在线下完成纸质报账单、原始附件单据、财务报表的归档工作。
1.2.3 财务共享系统应用过程中存在的问题
目前,财务共享系统利用报账单归集财务数据,自动将凭证信息推送至账表子系统形成会计凭证,应用账表子系统内的科目取数公式生成报表,处理过程中存在以下主要问题:
(1)在铁路财务会计管理信息系统内,财会数据共享平台建设工作尚未全面展开,财务共享系统仅与账表、资金结算子系统实现联通,还不能对接应收应付、固定资产、工资核算、铁路运输收入清算平台等其它财务子系统;债权债务的确认、清收、签认、账龄分析,固定资产增减变动、折旧计提,收付费清算、确认,职工工资计提、发放、结转等财务相关工作均需要业财人员在多个财务应用子系统中重复操作。
(2)铁路一体化信息集成平台开发和应用尚处于初步阶段,财务共享系统还不能通过该平台接入和集成国铁集团统建的相关业务系统的数据。目前,财务共享系统仅与铁路职工管理信息系统完成联通,实现组织机构、人员数据的共用,但数据同步频率不高,当更新的组织机构、人员数据未及时同步时,需要财务共享服务中心人员在财务共享系统中录入这些组织机构、人员数据,才能为相应的人员和组织提供服务。财务共享系统中的报账单仅能关联铁路物资管理信息系统中的出库单、入库单号,无法获取相关单据电子文档;业务人员在业务系统完成操作后,还要额外执行单据打印、扫描等繁琐步骤,先手动打印业务系统生成的单据,再将纸质单据扫描为电子影像文档并上传至财务共享系统,制约了会计档案的全面电子化。
(3)未联通企查查等外部系统,供应商及其银行账户信息需由业财人员分别在账表子系统、财务共享系统中重复录入信息和审核。
(4)财务共享系统虽已实现财务数据的初步汇聚,但缺乏完整的业务数据支持,无法实现数据统计与分析功能,致使财务共享服务中心数据应用部无法直接对各层级经营实体单位开展深入全面的经济活动分析,出具标准化的管理类会计报表,不能对各层级经营实体单位的费用构成、资金流向等信息进行监控,同时也掣肘了总账报表部自动生成动态报表、实施智能财务监控的职能落地,所汇聚的财务数据价值的没有得到充分的挖掘。
概而言之,由于财务共享系统与相关系统间存在信息壁垒,针对同一事项需要在不同系统内重复操作,特别是各业务系统已生成的财务报销凭证单据还需要经过手工打印、再扫描成电子文档上传的繁琐操作方式提报给财务共享服务中心,增加了业财人员工作量,极大地降低了业务处理流程的自动化程度和业务处理效率,因人工误操作导致的系统间数据不一致的风险也会增多,与相关业务系统的信息壁垒也阻碍了数据统计与分析的开发,对财务共享系统进一步功能拓展和完善形成了制约。
1.3 数据共享需求及所面临的挑战
1.3.1 与相关系统的数据共享需求
为完善财务共享系统,进一步提高报账业务流程的自动化程度,需要进一步与其它财务应用系统、国铁集团统建的业务系统、外部系统联通,获取相关数据,具体需求如表2所示。
表 2 与国铁集团统建的业务系统联进一步通及业务数据获取需求系统 主管部门 相关业务数据 固定资产核算子系统(V6.0) 财务部 资产名称、资产编号、入账原值等固定资产卡片信息 应收应付子系统 财务部 是否有合同、合同编码、合同名称、经济业务、收付款金额、收付款期限、责任人、责任部门、客商信息 铁路运输收入清算平台 财务部 铁路运输清算过程中产生的相关工作量指标,包括客运线路使用费、客运机车牵引服务费、车站旅客服务费、旅客列车上水作业服务费、售票服务费等工作量 企业管理和法律事务管理系统 企业管理和法律事务部 企业经营管理过程中产生的版式文件及数据,包括:中标文件、相关附件、依据附件、合同签订附件、合同解除变更信息附件、合同相对方信息等数据 铁路物资管理信息系统 物资管理部 企业物资日常管理过程中的相关数据及板式文件,包括:暂估、出库、调拨、处置、盘点、供应商信息等数据,入库单、出库单等版式文件 国铁通用物资采购平台
(国铁商城)物资管理部 企业线上采购过程中产生的相关订单信息,包括:账单编号、订单编号、商品名称、供应商信息等数据;电子发票等版式文件 货车系统 机辆部 货车全周期管理过程中产生的相关数据,涵盖新增、大修、维修、报废等 十八点统计分析系统 调度中心 铁路运输的组织、调度、指挥以及经营管理过程中产生的相关数据指标,包括:客票收入、货物运费、其他收入等数据,编组站调车、非编组站调车等工作量 铁路机车统计系统 发展和改革部 机车运用过程中的相关工作量指标,包括:内燃机车牵引总重、内燃机车运行用油、电力机车通过牵引总重、电力机车运行用电等 铁路客车技术管理信息系统
(KMIS系统)机辆部 客车运用、检修(新造)工作中的相关工作量指标,包括:客车维修、客车空调设备维修、客车段修、行李车维修、行李车段修等 铁路货车技术管理信息系统
(HMIS系统)机辆部 货车及配件资产日常管理过程中产生的相关数据,包括货车段修、大修等工作量 动车组管理信息系统
(EMIS系统)机辆部 动车组运用、检修过程中产生的相关工作量指标,包括动车组一级修、二级修,动力集中动车组维修、D1修、D2修、D3修、D4修等工作量 动力集中动车组管理信息系统
(CMIS系统)机辆部 动力集中动车组运用、检修过程中产生的相关工作量指标,包括动力集中动车组D5修、D6修等工作量 企查查 外部机构 供应商名称、纳税人识别号、开户行名称、银行账号、联合行号等 1.3.2 实现数据共享需求所面临的挑战
财务共享系统与上述系统实现联通、获取所需要的共享数据后,在实际使用数据时还面临着如下挑战。
(1)鉴于财务系统与业务系统在统计口径上存在差异,业财人员还需要完成整理业务数据的繁琐工作。由于不同职能部门对同一经济业务的管理侧重点、统计口径(主要是时间、范围)不完全相同,业务系统提供的源数据往往不能直接为业财人员所用。例如,铁路客车技术管理信息系统是对全路客车保有量按配属关系对客车进行分类管理,统计口径含铁路局代管客车(邮政车、非铁路局配属的国铁客车、地方铁路客车、特殊用途自备客车);账表子系统仅核算本企业配属客车的成本费用支出,不含铁路局代管客车;利用铁路客车技术管理信息系统中的统计数据对本企业配属客车运用、检修等作业成本进行分析前,业财人员需手工剔除铁路局代管客车的相关统计数据。
(2)公用数据的维护分散、重复,数据维护工作繁琐且负担沉重。以报账单凭证匹配规则为例,不仅需要财务共享服务中心根据各类业务涉及的会计科目和增挂的维度预先在财务共享系统中进行设置,还需要业财人员在账表子系统中选取、维护期初数据后,方可将凭证信息从财务共享系统成功推送至账表子系统。若来年会计科目发生较大变化,财务共享系统的报账单匹配规则和财会信息系统的科目维护工作量会在年初激增,影响财务开账工作。
(3)铁路财务应用系统、业务系统繁多,各系统功能和数据结构差异大,若缺乏统一规划与标准,不实施分级分类安全防护,会增加数据泄露、被篡改的隐患,使得数据安全风险难以精准应对。
2 系统设计
2.1 设计目标
财务共享应用数据中台(简称:中台)聚焦财务共享服务中心各岗位职能对财务、业务数据的共享需求,采集相关既有系统的数据,基于统一的数据标准和规范完成数据治理,实现对共享数据的集中管理,满足前端财务共享系统和其它财务应用系统功能完善的需要。
(1)创建数据目录:针对跨系统联通需求复杂、数据来源广泛的难题,创建公开、透明的数据目录,对纳入中台实现集中管理的来自财务应用系统、业务系统和外部系统的数据进行分类分级,实现共享数据快速定位与精准检索的同时,规范数据汇聚路径,避免重复采集数据。
(2)实现数据自动采集:采用标准化数据接口与流程自动化技术,自动采集各类数据,并对所采集的数据进行清洗,保证共享数据的规范性和完整性。
(3)提供统一的公用数据维护入口:面向国铁集团、铁路局集团公司、站段三个层级的用户,提供一个便捷、具有不同权限的统一数据维护操作入口,确保系统间公用数据能够出自同源。
(4)建立财务凭证及附件数据库:对各业务系统中涉及的财务凭证及其附件(如纸质发票扫描件、合同文档、电子发票、物资出入库单等)进行规范管理和集中存储,使各业务系统通过调用中台提供的接口服务,能够将其所生成的财务凭证附件文档直接上传至中台进行集中存储,为会计档案全面电子化集中管理提供有利条件。
(5)提供完善的数据安全防护机制:根据数据安全等级要求,采取身份认证、数据加密、数据脱敏等技术,对中台内数据进行安全防护,有效防范数据被泄露、篡改,筑牢数据安全防线。
2.2 架构设计
财务共享应用数据中台基于 B/S 模式开发,其架构如图3所示。
(1)基础层:利用铁路企业数据中心云平台提供的服务器、存储、网络等资源,构建中台运行环境。
(2)数据层:负责存储和管理数据,使用Oracle关系型数据库存储中台负责维护的组织机构数据、用户及授权数据、公用数据、数据维护日志等数据;采用文档数据库MongoDB存储财务凭证附件文档等非结构化数据;采用高性能分布式数据仓库存储所采集的财务和业务数据,并建立面向OLAP应用的数据存储模型,支持统计分析和数据挖掘应用;采用内存数据库Redis缓存会计科目结构、凭证匹配规则等频繁访问的数据,提高中台的响应速度和稳定性。
(3)服务层:基于开源ETL工具,支持可视化流程配置,构建数据采集引擎;采用日志管理工具,自动采集系统运行日志数据;采用Restful API 接口实现数据源系统、中台、数据使用方(财务共享系统、其它财务应用系统)之间的数据交互;采用数据加解密、数据备份等安全策略,提升数据传输与存储的安全性;采用数据压缩技术减少数据量,提高数据传输效率。
(4)应用层:面向财务共享系统、其它财务应用系统、相关业务系统以及中台用户,提供组织机构管理、用户及权限管理、数据目录管理、数据采集、公用数据维护、财务凭证管理、运行监控、安全防护等应用服务。
(5)展示层:使用VUE、ElementUI、CSS、HTML5等技术开发Web页面,支持国铁集团、铁路局、站段三级用户按权限使用浏览器登录中台进行相关操作。
2.3 基于数据中台的财务共享应用框架
部署财务共享应用数据中台后,财务共享应用框架如图4所示。
财务共享应用数据中台将财务共享系统既有的用户管理、数据维护、报账单扫描等功能剥离出来,加以拓展完善后,重新进行服务封装,建立数据目录实现共享数据的规范管理,完成数据自动采集,建立财务凭证库和财务凭证附件库,实现财务凭证集中管理,为财务共享系统和其它财务应用系统提供数据共享服务。
财务共享应用数据中台可以通过财会数据共享平台和铁路一体化信息集成平台采集共享数据,也可直接从其它财务应用系统、国铁集团其它业务系统、外部系统采集数据。
3 功能设计
中台用户分为财务共享服务中心和经营实体2大类,经营实体用户进一步划分为国铁集团、铁路局、站段3个层级,每个经营实体单位的用户包括1个系统管理员和多个数据维护员;财务共享服务中心用户包括1个财务共享服务中心系统管理员和多个数据维护员(数据应用部人员)。
3.1 组织机构管理
铁路局、国铁集团系统管理员及财务共享服务中心负责对财务系统与业务系统间公用的组织机构信息进行统一维护,中台自动记录每一项操作,确保所有操作均可追溯。
(1)行政组织机构信息维护:当铁路局及其下属各经营实体的行政组织机构(站段、非运输企业、控股合资公司等)发生变动时,或国铁集团直属各经营实体的行政组织机构(如各类专业公司)发生变动时,分别由铁路局系统管理员或国铁集团系统管理员利用从铁路职工管理系统的数据接口采集到的行政组织机构变动数据,完成行政组织机构信息库的新增、删除、修改等操作,并补全相关字段数据(如单位类别、单位分类、机构层级、统一社会信用代码等);若所创建的行政组织机构实体间存在上、下级关系,可通过设置下属节点,建立各级行政组织机构间的关联关系;数据中台自动记录铁路局、国铁集团系统管理员的数据维护操作日志,用于数据安全审计。
(2)财务组织信息维护:当财务组织机构(即核算主体)发生变动时,由财务共享服务中心系统管理员利用从账表子系统的数据接口采集到的财务组织机构变动数据,完成财务组织机构信息库的新增、删除、修改等操作,补全相关字段数据(决算级次、决算单位性质、决算行业属性、是否有效等);若创建的财务组织机构实体存在子公司,可通过设置下属节点,确定各财务组织机构之间的合并关系;对于一个行政组织机构下设有多个财务组织机构的情况(例如:基本建设单位按建设项目进行核算,一个基本建设的单位可能存在多个财务组织机构),可通过建立该行政组织机构与下设的多个财务组织机构的关联关系,以用于配置财务共享系统批量审批流程。
3.2 用户及权限管理
用户管理包括财务共享系统用户和中台用户的管理;各层级经营实体单位系统管理员和财务共享服务中心系统管理员负责完成用户信息维护及授权,对财务共享系统的用户信息进行统一维护和集中管理,最大程度减少重复工作,并保证用户数据的准确性及一致性。
(1)用户信息维护:各层级经营实体单位系统管理员利用铁路职工管理信息系统的数据接口采集到的本单位人员变动信息,完成用户信息(包含所属行政组织机构)的更新操作,补充相关字段数据(如用工类型、用工开期限开始、用工期限结束、差旅级别、开户行名称及卡号等),并根据财务业务关系,将该用户与相关的财务组织机构进行绑定。
(2)角色定义:财务共享服务中心系统管理员根据各层级用户在财务共享系统和中台内的操作和查询权限要求,创建各类角色,设置不同角色的名称、层级(集团总部/铁路局集团公司/站段)、类型(系统管理员、数据维护员、普通用户),并指定不同角色在财务共享系统和中台内的操作和查询权限。
(3)用户授权:根据管理职能和业务需求,各层级系统管理员为本单位的用户设置其角色;对于各层级普通用户,可批量完成在财务共享系统中的权限设置;财务共享服务中心系统管理员为本单位的用户设置其角色,完成用户授权。
3.3 数据目录管理
财务共享服务中心系统管理员对纳入中台管理的共享数据进行系统化梳理、分类和分级,完成业财数据目录的创建,帮助数据使用者快速、准确地找到所需数据,提高共享数据的可用性与利用效率,并可依据数据安全管理级别提供差异化安全防护。
(1)分类/分级定义:根据数据的来源和用途,将中台集中管理的数据划分为财务系统数据、业务系统数据和外部系统数据,进一步进行具体业务系统数据细化分类,创建相应的数据目录;根据数据的重要性、涉密程度等,将共享数据分为一般、敏感、核心3个等级,并据此提供差异化的安全防护[7]。
(2)源数据管理:平台管理员按照铁路企业共享数据资源管理规范,对各数据源相关信息进行维护,录入信息系统名称、主管部门、数据源类型(其它财务应用系统、业务系统、财会数据共享平台、铁路一体化信息集成平台)、数据源所在网域及其等保情况等信息,以及该系统包含的源数据种类名称;完成源数据的元数据管理,确保铁路业务数据统一规范管理,使共享数据资源更容易理解、查找、管理和使用。
(3)目录浏览与检索:按预定义的数据分类、数据来源信息系统、数据种类和元数据信息,将纳入中台管理的所有数据源进行层级化展示,方便用户查看可用的共享数据资源及其元数据信息;用户可按数据名称、数据分类、数据分级、数据来源信息系统和主管部门等查询条件,查询所需数据资源。
3.4 数据采集
结合数据更新频率与实时性要求、采集成本与维护难度、系统架构与集成需求等因素,中台主要采用拉取和推送两种方式从数据源获取相关数据。财务共享服务中心系统管理员完成采集流程配置,中台数据采集引擎据此自动从数据源采集所需数据,并完成数据清洗后,将数据存储在中台的数据库内,供前端应用(包括财务共享系统和其他财务应用系统)访问。
(1)数据源定义:数据源包括数据库、API数据源、文件数据源等类型。财务共享服务中心系统管理员完成相应的参数设置;其中,数据库类型的数据源参数包括连接参数、访问接口地址及参数、数据库驱动参数、数据库特定参数等;API数据源参数根据业务场景分为请求参数、数据格式参数、时间参数等;文件数据源参数与数据源类型有关,如JSON文件数据源需设置数据结构路径、文件完整性校验参数等。
(2)数据清洗规则定义:财务共享服务中心系统管理员使用开源ETL工具,设置数据转换、格式标准化、重复数据剔除、不相关数据处理、数据验证与逻辑检查等数据清洗规则,使所采集的数据符合规范。
(3)数据表参数设置:财务共享服务中心系统管理员设置中台内用于存储所采集的数据表的相关参数,包括数据表名称、存储数据参数(如数据类型、数据长度、取值范围、是否可为空等)等信息。
(4)数据自动采集:数据采集引擎根据数据源和数据清理规则定义,自动完成数据采集和清洗,并将数据存储在指定的目标表内。
3.5 公用数据维护
各层级数据维护员负责对铁路财务公用信息进行统一维护,确保公用数据在不同系统间的一致性,减轻财务共享服务中心数据应用部人员基础信息的配置的工作量和会计业务部、总账报表部、资金票据部人员单据审核的压力;数据中台自动记录每一项操作,确保所有数据维护操作均可追溯。
(1)供应商/客户信息维护:当各经营实体的供应商/客户信息发生变动时,由经营实体单位数据维护员根据财务共享系统“基础数据调整申请单”返回的供应商/客户基本信息(主要包括名称、纳税人识别号、银行账号、开户行、联行号等),以纳税人识别号作为唯一ID,利用中台与企查查的数据接口,查询供应商/客户信息,并与中台中的供应商/客户数据进行比对,完成供应商/客户信息审核,中台自动记录该数据维护员的操作日志。
(2)会计科目和维度维护:国铁集团系统管理员对全路标准会计科目结构进行维护,财务共享服务中心系统管理员根据本局实际需要,从中选取适用的会计科目和维度,形成本局的标准会计科目结构,中台自动记录系统管理员的操作日志。
(3)财务凭证匹配规则调整:当标准会计科目结构发生变化时,财务共享服务中心系统管理员完成财务凭证匹配规则的调整,包括会计科目与加挂维度、会计科目与部门预算、应收应付款项与现金流量项目等对应关系的设置,用于财务共享系统实现引导式填单,提高业务处理效率。
3.6 财务凭证管理
财务共享服务中心数据维护员对铁路企业所有非结构化财务凭证数据进行梳理和分类,形成完整、规范的财务凭证目录,中台为前端应用提供统一的财务凭证创建、附件上传与关联、财务凭证及附件查询服务,用于建立财务凭证库和财务凭证附件库,为会计档案全面电子化集中管理提供有利条件,减少纸质财务凭证打印操作。
(1)财务凭证目录定义:根据各业务系统中涉及的财务凭证附件种类,如纸质发票扫描件、合同文档、电子发票、物资出入库单等,按树状分类法进行分类,形成一个有层次的、逐级展开的非结构化财务凭证分类目录,并为每一个财务凭证种类指定具体业务系统来源、安全防护(敏感性)要求,用于业务系统数据接口定义、财务凭证分类台账创建、前端应用数据展示时进行数据脱敏处理的依据。
(2)财务凭证创建:为前端应用提供统一的财务凭证创建服务,用于为财务共享服务中心每一笔业务涉及的财务凭证创建相应财务凭证实体,中台根据财务凭证种类、凭证接收时间、凭证业务编号,自动为其生成内部唯一的财务凭证ID号,并将财务凭证实体存储在财务凭证库中。
(3)财务凭证附件上传与关联:为前端应用提供统一的财务凭证附件上传与关联服务,中台根据前端应用上传的每一个非结构化的财务凭证附件数据文档的文档类型(PDF、XML、JPEG等)、附件编号、摘要等,自动为其创建唯一ID号,将其与指定财务凭证实体建立关联,并将财务凭证与附件的关联信息保存在财务凭证库中,同时将财务凭证附件数据存储在财务凭证附件库(使用MongoDB存储[8])中,以实现财务凭证结构化数据与非结构化数据的统一归档管理。
(4)财务凭证查询:为前端应用提供统一的财务凭证查询服务,平台可按财务凭证种类、凭证接收时间、凭证业务编号,从财务凭证库中检索出相应的财务凭证数据,并返回给前端应用。
(5)财务凭证附件查询:为前端应用提供统一的财务凭证附件查询服务,中台可按财务凭证种类、凭证接收时间、凭证业务编号、附件编号、摘要等,先从财务凭证库中检索出对应的财务凭证附件ID号,再根据财务凭证附件ID号,从财务凭证附件库中检索出相应的财务凭证附件数据,返回给前端应用。
3.7 运行监控
为各层级系统管理员提供可视化监控界面,追踪数据维护过程,监控中台内部各组件健康状态,监视中台运行情况,确保数据合规维护、中台运行处于正常状态。
(1)数据维护日志查看:查看各类数据维护过程以及各个数据维护员的维护操作,检查是否存在操作错误或违规操作。
(2)系统运行日志查看:查看中台内部各组件的运行情况,包括服务状态、资源使用情况、操作行为、数据传输记录、事务处理状态等,必要时进行扩容和性能调优。
(3)系统运行监控:对中台运行过程中系统资源占用、数据处理吞吐量、服务运行性能等进行监控,当出现响应时间过长、服务崩溃、请求超时等异常情况,启动故障排查,确保中台正常运行。
3.8 安全防护
在数据采集、传输、存储和使用的过程中,提供身份认证、数据加密、数据脱敏等安全防护服务,保障数据安全。
(1)身份认证:对业务系统、财务系统等数据来源进行身份认证,确保只有经过授权的合法系统才能向中台提供数据,采用密码认证、多因素认证等技术,验证数据源的真实性,防止非法数据源接入。
(2)数据加密:对于核心数据采用加密算法进行加密处理,将明文数据转换为密文数据。只有拥有相应密钥的授权用户才能解密和访问原始数据,如对列车运行数据进行加密处理,去除或改变敏感内容。同时,定期更新加密算法和密钥,提高加密安全性。
(3)数据脱敏:对于中台内一般数据采用替换方式,将数据中的某些字符或字段用其他字符或固定值替换,去除敏感内容。
4 结束语
与相关系统的信息壁垒,对财务共享系统进一步功能拓展和完善形成了制约。为此,提出财务共享应用数据中台设计,将财务共享系统既有的用户管理、数据维护、报账单扫描等功能抽离出来,重新进行服务封装,建立数据目录,实现共享数据的规范管理,并完成共享数据自动采集,建立财务凭证库和财务凭证附件库,实现财务凭证集中管理,为财务共享系统、其它财务应用系统及相关业务系统提供数据共享服务。在财务共享应用数据中台的支持下,财务共享系统的功能完善、拓展和流程优化提供了良好的数据基础。财务共享应用数据中台的研究开发,是在财会数据共享平台和铁路一体化信息集成平台尚未形成支撑能力前,通过建立面向专项应用的数据共享机制,加快专项应用系统功能优化和完善的积极探索。
目前,财务共享应用数据中台在中国铁路成都局集团有限公司进行试点,在中台的支持下,将物资批量报账业务处理加入财务共享系统,能够依据中台设置的财务凭证匹配规则,实现引导式物资批量报账填单,极大地提高了业务处理效率。后续将聚焦数据采集,与数据源系统研发单位紧密配合,加快推进数据共享的范围,对财务共享系统的功能进行拓展和优化,不断拓展和提升对该系统对财务共享服务中心各项业务的支持,增强财务共享服务中心在铁路企业财务集中管控方面的能力。
-
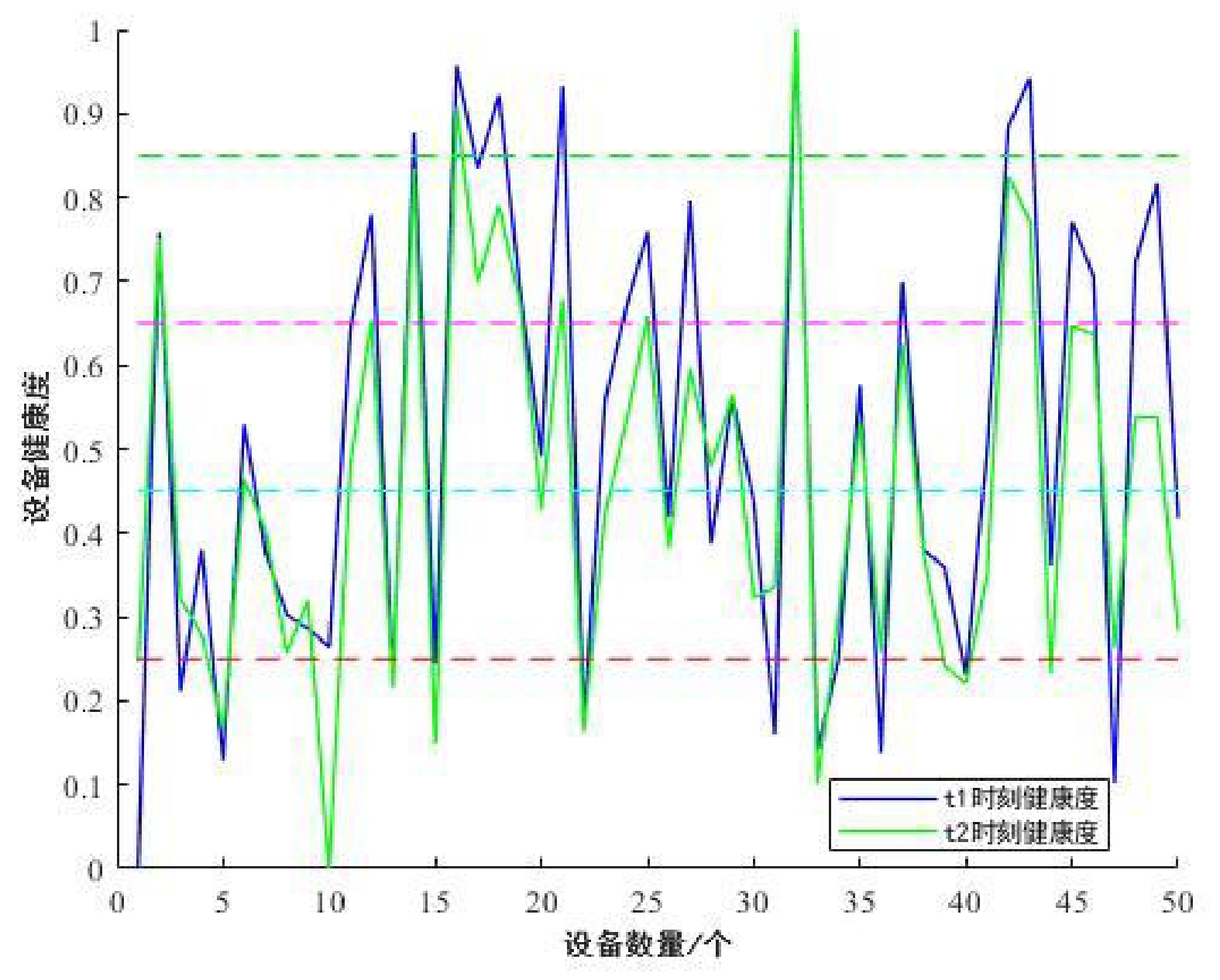
表 1 票务设备健康状态等级划分
等级 健康度取值范围 健康等级 状态描述 I [0.85,1] 健康 指标处于正常范围且靠近最佳值,设备安全 II [0.65,0.85) 亚健康 指标基本合格,无劣化趋势,设备比较安全 III [0.45,0.65) 注意 小部分指标接近警告值,大部分指标基本合格,有劣化趋势,应加强检测并排除故障 IV [0.25,0.45) 警告 指标接近警告值,有劣化趋势,应尽快安排检修 V [0,0.25) 故障 机组运行状况异常,指标数据超过阈值,设备无法运行,必检修 表 2 票务设备健康评价指标
目标层 准则层 指标层 指标属性 票务设备
健康状态A1设备性能B1 故障发生频次/年E1 越小越优型 平均故障间隔时间(MTBF)E2 越大越优型 平均修复时间(MTTR)E3 越小越优型 运行工况B2 累计工作时长E4 越大越优型 无故障运行时长E5 越大越优型 运行环境质量E6 越大越优型 维护保养B3 巡检计划完成率/年E7 越大越优型 保养计划完成率/年E8 越大越优型 故障维修响应E9 越小越优型 表 3 设备评价指标权重值
指标 E1 E2 E3 E4 E5 E6 E7 E8 E9 wj 0.15 0.09 0.35 0.04 0.10 0.02 0.05 0.03 0.17 μj 0.10 0.11 0.11 0.12 0.11 0.11 0.11 0.12 0.11 Wj 0.13 0.11 0.23 0.08 0.10 0.06 0.08 0.08 0.14 表 4 设备寿命预测性能比较
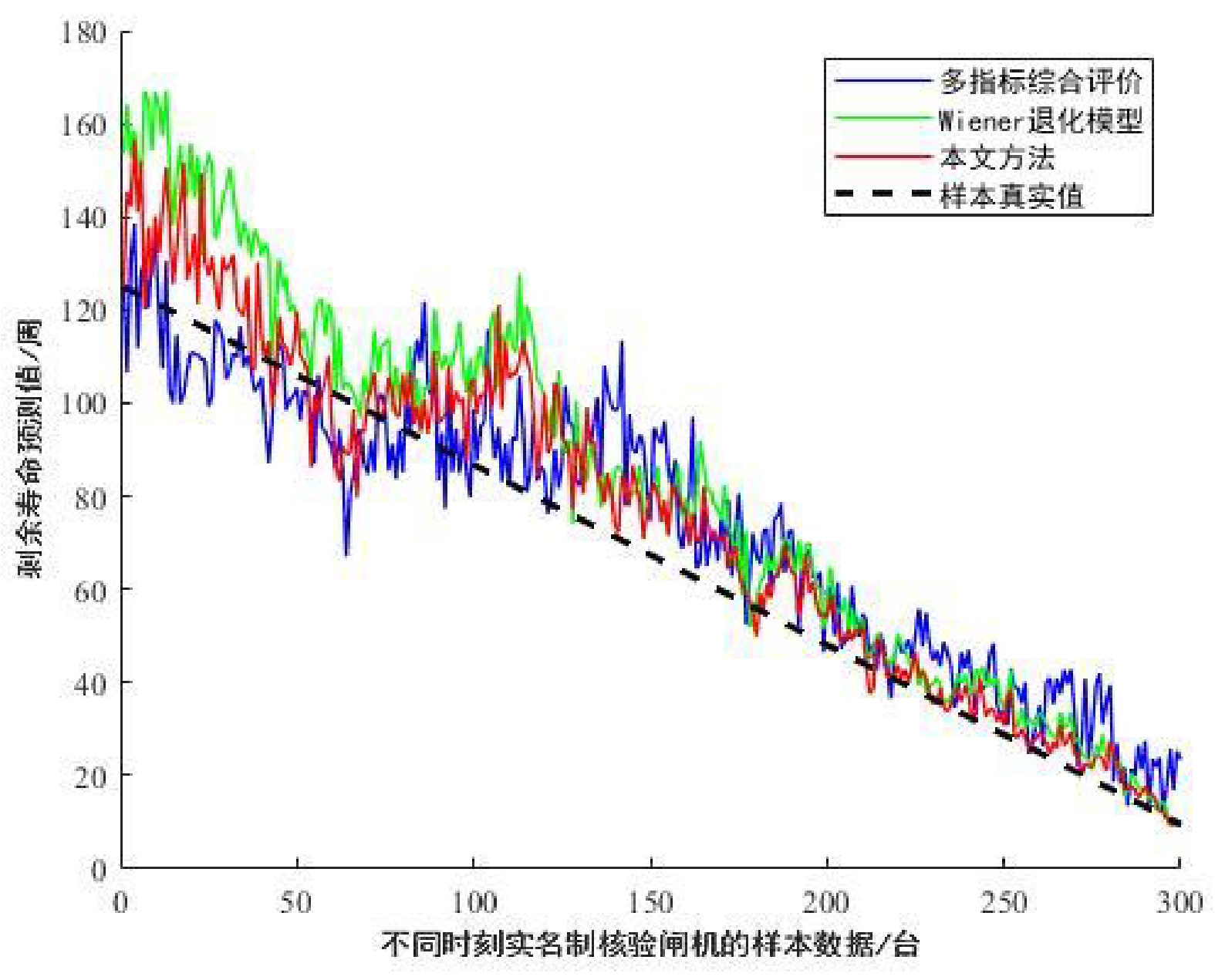
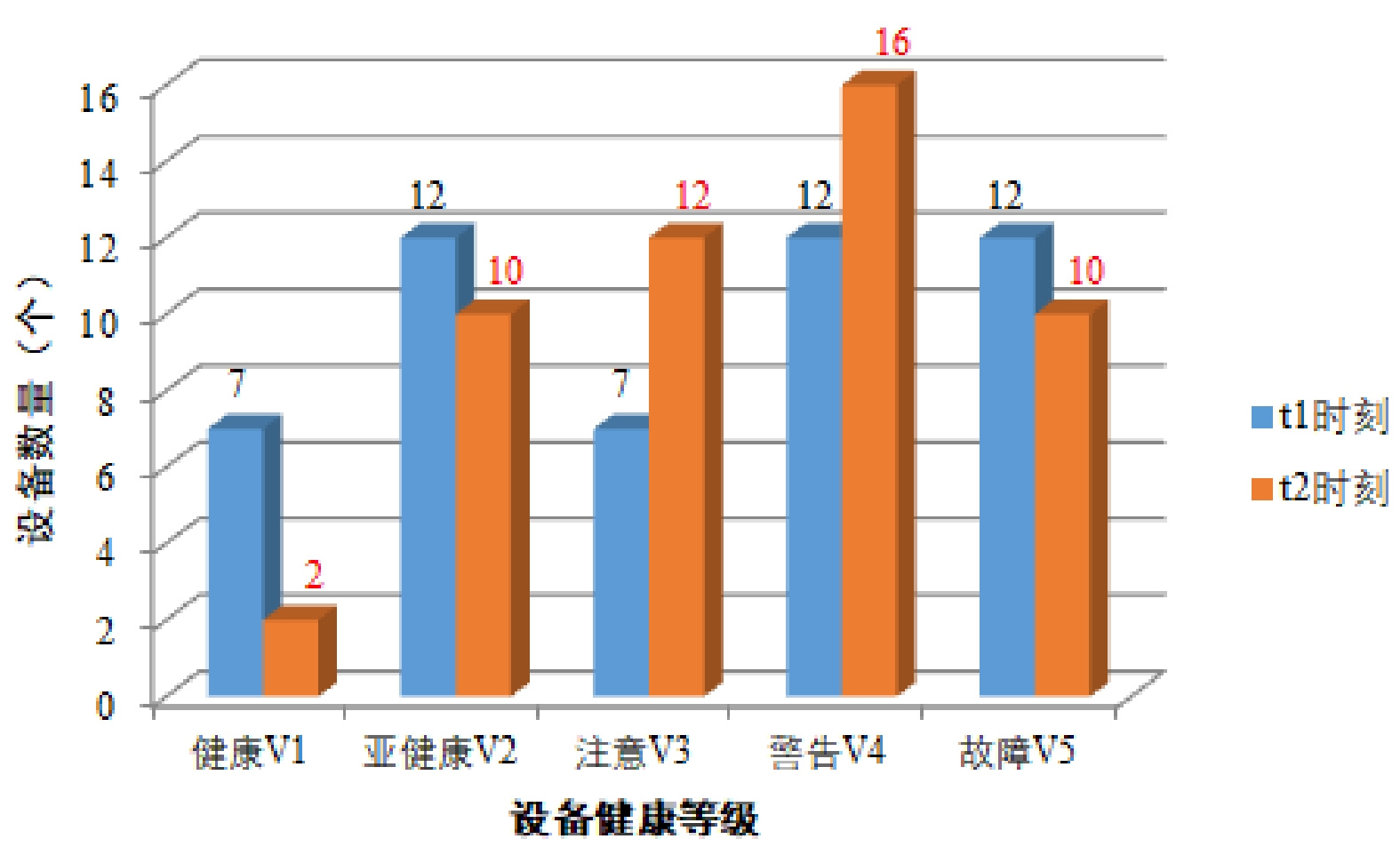
预测方法 RMSE MAPE 平均准确率 多指标综合评价模型H 13.50 0.17 82.55% Wiener退化模型Z(t) 17.75 0.18 82.29% 优化的评估模型H′ 11.67 0.11 88.16% 表 5 在役设备t1时刻初始化运行数据
设备编号 E1 E2 E3 E4 E5 E6 E7 E8 E9 1 0.43 0.08 0.86 0.21 0.00 0.83 0.12 0.90 0.31 2 0.80 0.29 0.67 0.41 0.70 0.38 0.23 0.14 0.53 … … … … … … … … … … 49 0.10 0.94 0.12 0.39 0.77 0.09 0.27 0.79 1.00 50 0.69 0.56 0.66 0.04 0.39 0.98 0.39 0.39 0.14 -
[1] Cubillo A, Perinpanayagam S, Esperon-Miguez M. A review of physics-based models in prognostics: Application to gears and bearings of rotating machinery[J]. Advances in Mechanical Engineering, 2016, 8(8): 1-21.
[2] 高锋阳,王文祥,张浩然,等. 基于状态和风险评估的无接触网城轨车辆电气系统运维策略[J]. 中国铁道科学,2022,43(4):148-156. DOI: 10.3969/j.issn.1001-4632.2022.04.16 [3] Zhang Z X, Si X S, Hu C H, et al. Degradation data analysis and remaining useful life estimation: A review on wiener-process-based methods[J]. European Journal of Operational Research, 2018, 271(3): 775-796. DOI: 10.1016/j.ejor.2018.02.033
[4] 孙振铎,侯东勃,李 伟,等. 基于裂纹萌生和扩展的渗氮钢疲劳寿命预测[J]. 兵器材料科学与工程,2021,44(5):76-82. DOI: 10.14024/j.cnki.1004-244x.20210729.001 [5] 王愈轩,刘尔佳,黄永章. 数据驱动下的综合能源系统短期多元负荷预测[J]. 计算机工程与设计,2022,43(5):1435-1442. DOI: 10.16208/j.issn1000-7024.2022.05.031 [6] Babu G S, Zhao P L, Li X L. Deep convolutional neural network based regression approach for estimation of remaining useful life[C]//Proceedings of the 21st International Conference on Database Systems for Advanced Applications, 16-19 April, 2016, Dallas, USA. Cham: Springer, 2016: 214-228.
[7] 李 炜,张盼盼,蒋栋年. 基于DAE-MD的电源车柴油机健康状态量化评估方法[J]. 兰州理工大学学报,2019,45(6):78-84. DOI: 10.3969/j.issn.1673-5196.2019.06.015 [8] Atoui M A, Cohen A. Coupling data-driven and model-based methods to improve fault diagnosis[J]. Computers in Industry, 2021 (128): 103401. DOI: 10.1016/j.compind.2021.103401
[9] 李天梅,司小胜,刘 翔,等. 大数据下数模联动的随机退化设备剩余寿命预测技术[J]. 自动化学报,2022,48(9):2119-2141. DOI: 10.16383/j.aas.c201068 [10] Zhang H W, Li Q, Sun Z N, et al. Combining data-driven and model-driven methods for robust facial landmark detection[J]. IEEE Transactions on Information Forensics and Security, 2018, 13(10): 2409-2422. DOI: 10.1109/TIFS.2018.2800901
[11] Yan H, Liu K B, Zhang X, et al. Multiple sensor data fusion for degradation modeling and prognostics under multiple operational conditions[J]. IEEE Transactions on Reliability, 2016, 65(3): 1416-1426. DOI: 10.1109/TR.2016.2575449
[12] 彭开香,皮彦婷,焦瑞华,等. 航空发动机的健康指标构建与剩余寿命预测[J]. 控制理论与应用,2020,37(4):713-720. DOI: 10.7641/CTA.2019.90039 [13] Hu C H, Pei H, Si X S, et al. A prognostic model based on DBN and diffusion process for degrading bearing[J]. IEEE Transactions on Industrial Electronics, 2020, 67(10): 8767-8777. DOI: 10.1109/TIE.2019.2947839
[14] 裴 洪,胡昌华,司小胜,等. 不完美维护下基于剩余寿命预测信息的设备维护决策模型[J]. 自动化学报,2018,44(4):719-729. DOI: 10.16383/j.aas.2017.c160534 [15] 李进友,李 媛,冯 冰,等. 基于随机组合赋权模糊评价的风电机组健康状态评估[J]. 太阳能学报,2022,43(8):340-351. DOI: 10.19912/j.0254-0096.tynxb.2020-1416 [16] 杨春波,陶 青,张 健,等. 基于综合健康指数的设备状态评估[J]. 电力系统保护与控制,2019,47(10):104-109. DOI: 10.7667/PSPC20191014




 下载:
下载: