Prediction method of railway faults duration based on convolutional neural network
-
摘要: 随着铁路网络复杂程度的不断提高，铁路运营部门调度难度日益增加，亟须研究精准预测铁路故障持续时间的方法，从而提高铁路调度系统应对各类风险和事故的能力。文章基于“安监报1”的文本数据，结合Jieba分词、Word2vec词向量模型等自然语言处理技术，构建了一种基于卷积神经网络（CNN，Convolutional Neural Network）的铁路故障持续时间预测模型，并基于中国铁路沈阳局集团有限公司的实际生成数据进行试验。试验结果表明，本预测模型能够较为快速、准确地获取铁路故障持续时间及其概率分布，为列车的运行调整提供参考。
-
关键词:
- 铁路故障持续时间 /
- 自然语言处理 /
- 卷积神经网络（CNN） /
- Word2vec /
- 安监报1
Abstract: With the continuous increase in the complexity of railway networks, the scheduling difficulty of railway operation departments is increasing. It is urgent to study methods for accurately predicting the duration of railway failures, in order to improve the ability of railway dispatch systems to cope with various risks and accidents. This paper was based on the text data of "Safety Supervision Report 1", combined with natural language processing techniques such as Jieba word segmentation and Word2vec word vector model, to construct a railway fault duration prediction model based on Convolutional Neural Network (CNN). The model was tested based on actual generated data from China Railway Shenyang Group Co. Ltd. The experimental results show that this prediction model can quickly and accurately obtain the duration and probability distribution of railway faults, and provide reference for train operation adjustment. -
铁路运输调度系统应对各类风险和事故的能力一直是铁路运营部门关注的重点。快速准确地预测故障持续时间，可为调度指挥提供参考，是提升风险应对能力的关键。当前，发生故障或扰动时，列车调度员只能凭借自己的经验，判断故障的持续时间，这使得判断的结果误差大、稳定性低、主观性强。为此，铁路运营部门迫切需要运用一种快速、高效的铁路故障持续时间预测方法，以满足日常列车运行调整的需求。
目前，一种逐渐成熟的计算机技术——自然语言处理，已经成为计算机科学领域与人工智能领域的一个重要研究方向，研究人与计算机间通过自然语言进行有效通信的各种理论和方法。深度学习作为机器学习领域中的一个重要分支，最早应用于计算机视觉领域，近些年来，也开始在自然语言处理领域得到运用，使得自然语言处理的语言建模、语义解析和文本分类等多项工作取得了突破。Mikolov等人[1-2]提出了用CBOW和Skip-gram模型对文本分布进行表示，能够在不丢失词语间相关性的情况下，将词语映射到低纬度的向量空间中，降低计算量，提高模型的计算效率；Kalchbrenner等人[3]构建了一个动态卷积神经网络（CNN，Convolutional Neural Network）模型，从而处理不同长度的文本；吴龙峰[4]针对短文本的文本分类中出现的特征维度高和数据稀疏的问题，提出了一种结合Word2vec词向量模型和LDA（Latent Dirichlet Allocation）主题模型的文本特征表示模型，增强了模型的特征表达能力；牛雪莹[5]结合Word2vec词向量模型和LDA主题模型，构建CNN模型进行文本分类，并利用实际数据验证了方法的有效性。
由于铁路行业内存在大量的非结构化文本数据，自然语言处理技术在铁路行业具有一定的应用前景[6]。已有学者开始应用自然语言处理技术解决铁路异物侵限、故障诊断、轨道形变检测和事故致因分类等问题。Rosadini等人[7]提出利用自然语言处理技术处理铁路信号制造商的文件，从中挖掘出铁路需求中存在的缺陷；樊梦琳[8]在事故报告文本挖掘和事故特征选择的基础上，根据铁路事故持续时间的分布特点设计了结合分类和回归的双层预测模型，并利用XGBoost算法构建模型预测铁路事故的持续时间；张世同[9]构建了基于BERT与BiLSTM的文本分类模型，通过分析安监报文本数据来确定隐患分类。目前，直接利用铁路事故文本报告，对故障持续时间进行预测的相关研究尚少。
本文利用自然语言处理技术处理“安监报1”文本数据，建立基于CNN的铁路故障持续时间预测模型，快速、高效地得出故障的持续时间及其概率分布，从而为列车调度员的实时列车运行计划调整决策提供参考。
1 预测模型建立
1.1 数据预处理
铁路交通事故（设备故障）概况表又称为“安监报1”，描述的内容包括铁路故障发生的时间、地点、事故详情、处理方式和持续时间等信息。由于故障的持续时间存在一定的规律性，即相同类型故障的处理流程是一致的，持续时间差别不大，从而为利用“安监报1”文本数据进行铁路故障持续时间预测提供了理论前提。然而“安监报1”作为一种非结构化文本数据，将其作为CNN模型的输入参数前，需要先对其进行数据预处理。
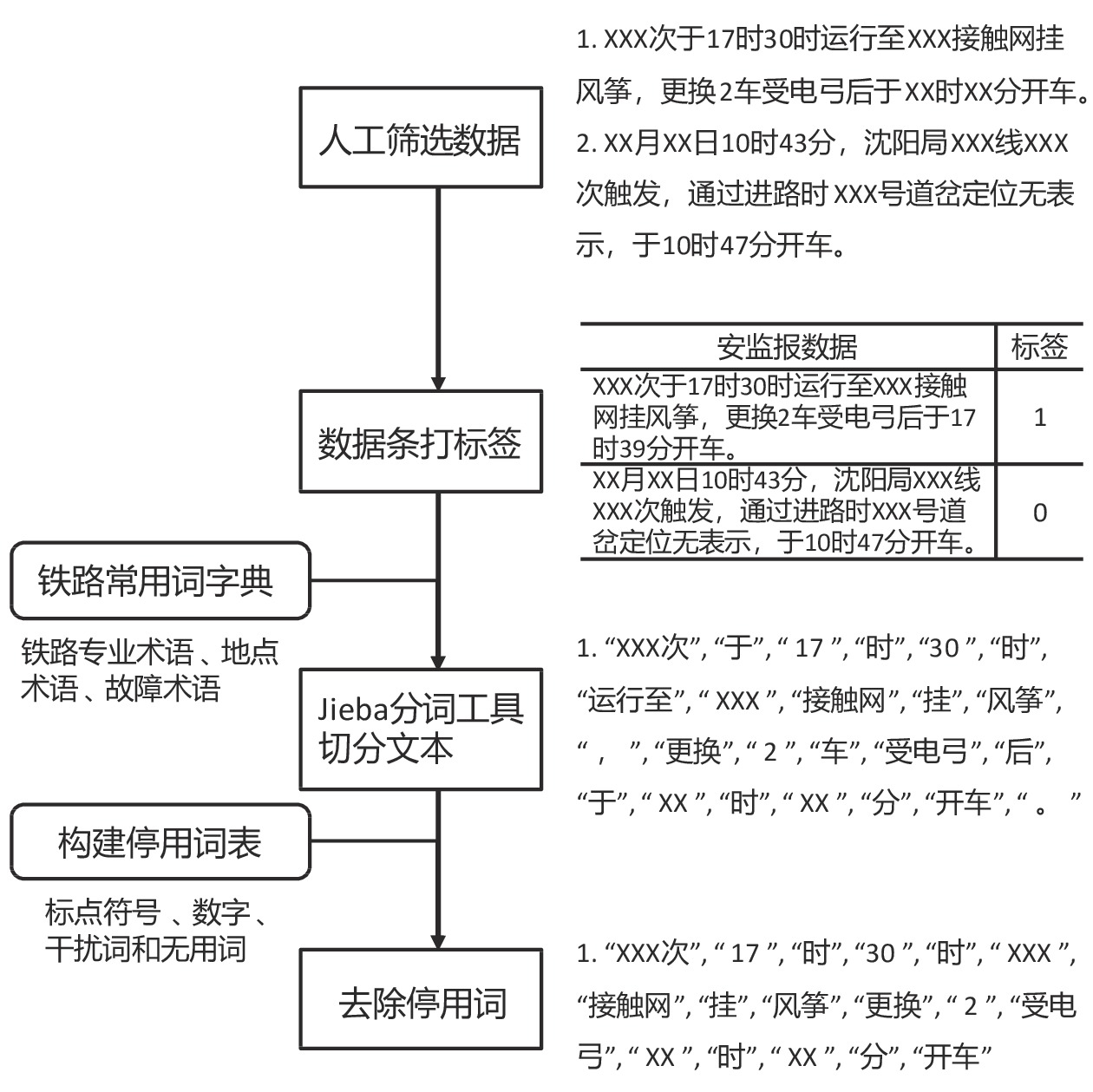
“安监报1”文本数据的预处理过程包括人工筛选数据、数据条打标签、利用Jieba分词工具切分文本、构建停用词表并去除停用词，如图1所示。
（1）由于“安监报1”的记录还包含未造成运营影响的故障情况和故障情况不明的数据条，需要对这些数据进行人工筛选，并删去这些对铁路故障持续时间预测无实际作用的数据条；
（2）根据实际需求将故障持续时间划分为若干个类别，并给每条可用的数据条打上标签；
（3）利用Jieba分词工具对每条数据文本进行切分，文本切分是自然语言处理的基础，切分的准确度直接决定了词向量的质量。Jieba分词工具支持3种分词模式，包括精确模式、全模式和搜索引擎模式。本文采用精确模式，此模式可将句子进行精确切分，更适合文本分析任务。此外，为防止“安监报1”文本数据中的一些特有名词被误切分，可在Jieba分词工具中嵌入一个铁路常用词字典，其包含常用的铁路术语、地点术语和故障术语等，例如“客专线”“撞鸟”“制动轴”等。
（4）构建适用于铁路领域的停用词表，去除切分后的数据中包含的标点符号、数字、干扰词和无用词等，例如：“检查”“于”“运行”等。
1.2 铁路故障持续时间预测模型
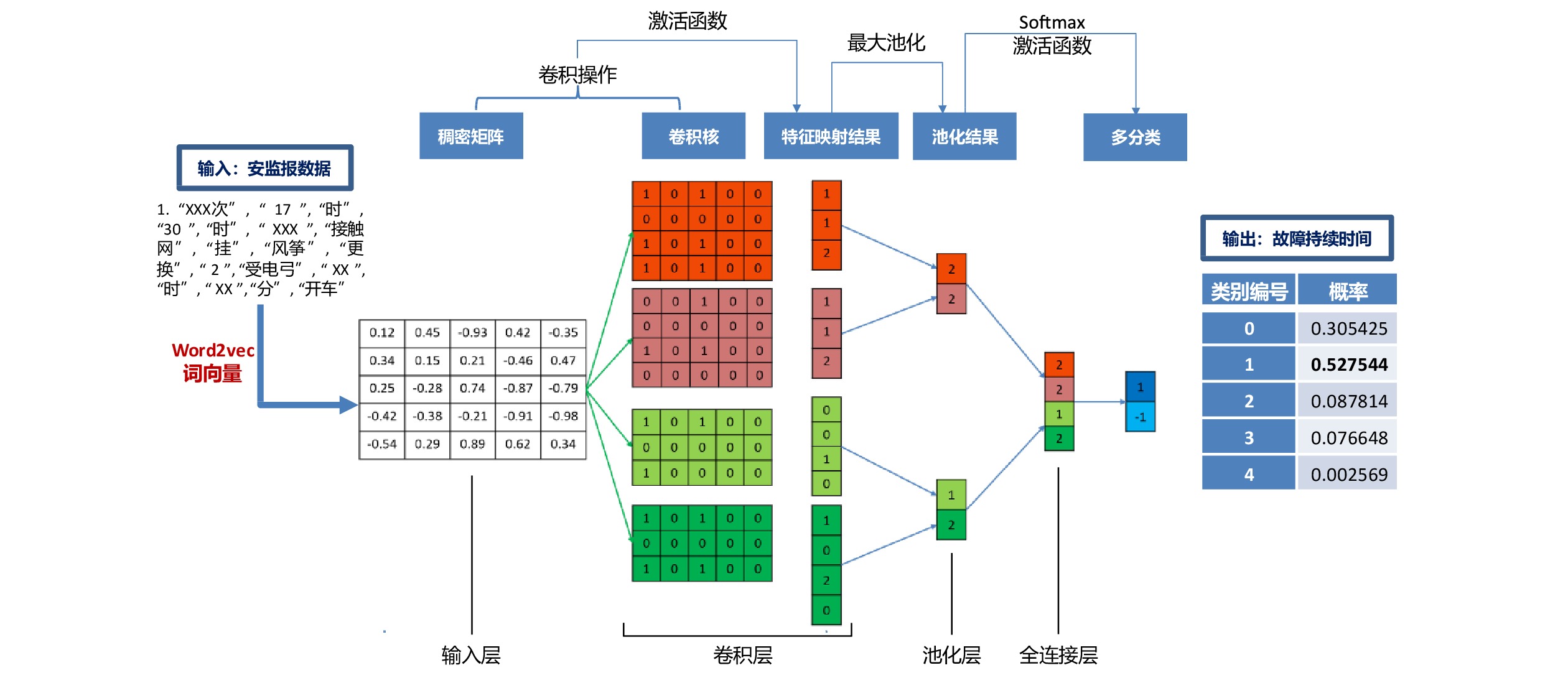
本文基于CNN构建铁路故障持续时间预测模型，将CNN多分类的结果设置为预测的时间范围。在预测模型实际运用时，列车调度员输入描述故障的文本信息后，经过数据预处理和该预测模型的计算，即可得到铁路故障的持续时间及概率分布。该预测模型由输入层、卷积层、最大池化层和全连接层组成，模型架构如图2所示。
1.2.1 输入层
将预处理后的数据输入至输入层，为使得文本数据能够被计算机所理解，需要将非结构化、不可计算的文本数据转化为结构化、可计算的向量，即数字信息。本文利用Word2vec词向量模型计算得到低维度的稠密矩阵。该模型是一种基于神经网络的词向量生产模型，利用深度学习网络对语料数据的词语及其上下文的语义关系进行建模，从而得到低维度的词向量，即稠密矩阵，可在保留词与词间关系的同时，显著提高求解效率，已广泛应用于自然语言处理领域。
1.2.2 卷积层
将输入层处理后的低维度的稠密矩阵输入至卷积层，进行卷积操作。本文通过设置不同大小的卷积核，对输入的稠密矩阵进行多次卷积操作，提取文本的关键特征。每一次卷积操作相当于一次特征向量的提取，通过定义不同的卷积窗，提取不同的特征向量，构成卷积层的输出，即图中的特征映射结果。
1.2.3 池化层
将卷积操作后的特征映射结果输入至池化层，进行池化操作。在池化层中，不同维度的特征映射结果经过池化层后都能变成定长的向量。本文采用最大池化的方式，取特征映射结果的最大值。最大池化既可保留文本的突出特征，又对特征映射结果进行了降维，从而降低了预测模型的数据运算量，以便更好地捕捉文本数据中描述故障的关键信息。图2中特征映射结果经过最大池化由三维向量降为一维向量。然而，最大池化不可避免地会损失一些有效信息，一般可通过增加特征映射数量的方式进行弥补，本文设计的卷积层包含200个特征映射，可在一定程度上弥补信息的损失。
1.2.4 全连接层
将最大池化层处理后的数据输入全连接层。全连接层在CNN中起到分类器的作用。数据通过全连接的方式接入到全连接层后连接到多维的时间类别向量上，该向量就是安监报文本数据在设定的故障持续时间范围上的概率分布情况，其中，最大概率值为预测的故障持续时间类别。
2 实验结果与分析
2.1 实验数据和环境
本文的实验数据来源于中国铁路沈阳局集团有限公司，选取其2017年至2021年“安监报1”的文本数据，总计9000条。选取该数据集的80%作为训练集、20%作为测试集。展示出的数据已经过脱敏处理，实验数据样例如表1所示。
表 1 “安监报1”实验数据样例“安监报1”数据 XXX次于17时30分时运行至辽阳高速场至沈阳南站间接触网挂风筝，经随车机械师检查确认风筝挂在7车受电弓上，更换2车受电弓后
于17时47分开车。XXX次列车运行至阜新站至黑山北站间XXX处撞野鸡，17时02分黑山北站
停车检查，经随车机械师下车检查无异常后17时08分开车，影响本列
超站停4 min。本实验基于Keras框架，搭建铁路故障持续时间预测模型。Keras是建立在TensorFlow和Theano上的神经网络框架，采用类似搭积木的方式来构建神经网络。实验具体环境为：CPU AMD 5800H，内存16 G，编程语言为Python3.6，开发工具为Visual Code，深度学习框架为TensorFlow 1.0.0。
2.2 实验参数设置
本文中的数据统一设置为UTF-8格式，利用Python调用Jieba分词组件对数据进行分词，并利用构建的停用词表来去除干扰词。本实验的故障持续时间类别设置如表2所示，卷积神经网络的具体参数配置如表3所示。
表 2 故障持续时间类别标签编号 时间范围/min 0 （0, 5） 1 [5, 30） 2 [30, 60) 3 [60, 180） 4 [180, +∞) 表 3 卷积神经网络参数配置表参数名 参数值 卷积核个数 256 卷积核大小 3 嵌入层维度 100 单词训练数据个数 256 轮次 24 验证集比例 0.2 丢弃率 0.3 激活函数 Softmax 池化方式 MaxPool 2.3 预测结果与分析
训练集数据共7200条，模型的训练时间约为274 s。测试集数据共1800条，测试时间约为16.3 s，平均每条数据花费的时间约为0.009 s，能够满足调度现场的实时性需求。模型的输出结果为各类别的概率，即故障持续时间的概率，预测结果样例如表4所示。测试集的准确率为72%，损失值为2.3789。
表 4 预测结果样例安监报数据 类别0 类别1 类别2 类别3 类别4 XXX次于17时30分时运行至辽阳高速场至沈阳南站间接触网挂风筝，经随车机械师
检查确认风筝挂在7车受电弓上，更换2车受电弓后于17时47分开车。0.075 0.820 0.078 0.025 0.001 XXX次列车运行至阜新站至黑山北站间XXX处撞野鸡，17时02分黑山北站停车
检查，经随车机械师下车检查无异常后17时08分开车，影响本列超站停4 min。0.153 0.003 0.025 0.780 0.038 本模型的输出结果能够较为直观地展现故障持续时间在各时间范围内的概率，具有良好的可读性。从实验结果来看，测试集准确率约为72%，能够为列车调度员在铁路故障突发时预测故障持续时间提供参考，具有一定的实际应用价值。
3 结束语
本文利用自然语言处理技术，将Word2vec词向量模型与基于CNN的分类模型相结合，设计了铁路故障持续时间预测模型。该预测模型能够快速、准确地得出故障持续时间的概率分布，从而为列车运行调整提供参考。
同类型故障的持续时间横跨多个时间范围、“安监报1”数据不够规范且无法全面描述故障详情、持续时间较长的数据样本较少等原因制约了本文模型的准确率。下一步，应针对“安监报1”数据不够规范的问题，引入更为规范化和描述更为细致的数据。
-
表 1 “安监报1”实验数据样例
“安监报1”数据 XXX次于17时30分时运行至辽阳高速场至沈阳南站间接触网挂风筝，经随车机械师检查确认风筝挂在7车受电弓上，更换2车受电弓后
于17时47分开车。XXX次列车运行至阜新站至黑山北站间XXX处撞野鸡，17时02分黑山北站
停车检查，经随车机械师下车检查无异常后17时08分开车，影响本列
超站停4 min。
下载: 导出CSV
表 3 卷积神经网络参数配置表
参数名 参数值 卷积核个数 256 卷积核大小 3 嵌入层维度 100 单词训练数据个数 256 轮次 24 验证集比例 0.2 丢弃率 0.3 激活函数 Softmax 池化方式 MaxPool
下载: 导出CSV
表 4 预测结果样例
安监报数据 类别0 类别1 类别2 类别3 类别4 XXX次于17时30分时运行至辽阳高速场至沈阳南站间接触网挂风筝，经随车机械师
检查确认风筝挂在7车受电弓上，更换2车受电弓后于17时47分开车。0.075 0.820 0.078 0.025 0.001 XXX次列车运行至阜新站至黑山北站间XXX处撞野鸡，17时02分黑山北站停车
检查，经随车机械师下车检查无异常后17时08分开车，影响本列超站停4 min。0.153 0.003 0.025 0.780 0.038
下载: 导出CSV
-
[1] Mikolov T, Sutskever I, Chen K, et al. Distributed representations of words and phrases and their compositionality[C]//Proceedings of the 26th International Conference on Neural Information Processing Systems, 5-10 December, 2013, Lake Tahoe Nevada. Red Hook, USA: Curran Associates Inc. , 2013.
[2] Mikolov T, Chen K, Corrado G, et al. Efficient estimation of word representations in vector space[J]. arXiv preprint arXiv: 1301, 3781: 2013.
[3] Kalchbrenner N, Grefenstette E, Blunsom P. A convolutional neural network for modelling sentences[C]//Proceedings of the 52nd Annual Meeting of the Association for Computational Linguistics, 22-27 June, 2014, Baltimore, MD, USA. Baltimore: ACL, 2014.
[4] 吴龙峰. 基于Word2vec和LDA的卷积神经网络文本分类模型[J]. 电脑知识与技术,2019,15(22):203-204,206. DOI: 10.14004/j.cnki.ckt.2019.2755 [5] 牛雪莹. 结合主题模型词向量的CNN文本分类[J]. 计算机与现代化,2019(10):7-10. DOI: 10.3969/j.issn.1006-2475.2019.10.002 [6] 张浩然,谢云熙,张艳荣. 基于TextCNN的文本情感分类系统[J]. 哈尔滨商业大学学报(自然科学版),2022,38(3):285-292. [7] Rosadini B, Ferrari A, Gori G, et al. Using NLP to detect requirements defects: an industrial experience in the railway domain[C]//Proceedings of the 23rd International Working Conference on Requirements Engineering: Foundation for Software Quality, 27 February –2 March, 2017, Essen, Germany. Cham: Springer, 2017: 344-360.
[8] 樊梦琳. 铁路事故持续时间预测方法研究[D]. 北京:北京交通大学,2020. [9] 张世同. 基于BERT与BiLSTM的铁路安监文本分类方法[J]. 现代计算机,2021(22):38-42. -
期刊类型引用(2)
1. 沙淼，张可心，刘志刚，邱瑞昌，陈杰. 基于目标速度追踪的城轨列车节能优化算法. 都市快轨交通. 2023(06): 40-48 . 
百度学术
2. 马阳阳，孟学雷，贾宝通，任媛媛，秦永胜. 基于列车运行时间偏差惩罚的高速列车节能优化方法. 交通信息与安全. 2021(04): 84-91 . 百度学术
其他类型引用(13)
计量
- 文章访问数: 98
- HTML全文浏览量: 41
- PDF下载量: 56
- 被引次数: 15
