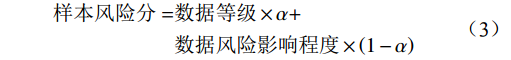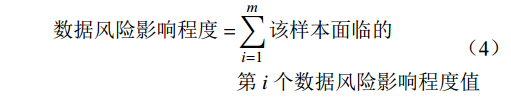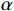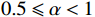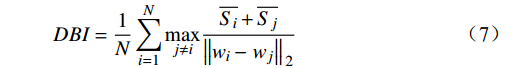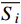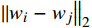Risk level classification method for railway network data based on GMM clustering
-
摘要: 铁路行业信息基础设施及重要信息系统产生的数据种类繁多、数量庞大且价值密度高,而不同类型或等级的铁路网络数据存在不同级别的安全风险。为了完善铁路网络数据风险评估机制,设计一种基于高斯混合模型(GMM,Gaussian Mixture Model)聚类的铁路网络数据风险等级分类方法。从数据和风险角度提取关键信息,构建风险信息数据集;通过K-means聚类获得初始聚类中心;基于混合距离计算进行GMM聚类,实现数据风险等级划分。经实验验证,与传统K-means聚类、谱聚类算法相比,GMM聚类算法对铁路网络数据的聚类效果更优,能够更加准确地对铁路网络数据进行风险等级分类,从而为进一步落实铁路网络数据安全管理要求提供重要的技术支撑。
-
关键词:
- 高斯混合模型(GMM)聚类 /
- K-means聚类 /
- 最大期望(EM)算法 /
- 铁路网络;数据风险 /
- 风险等级分类
Abstract: The information infrastructure and important information systems in the railway industry generate a wide variety of data types, large quantities, and high value density, and different types or levels of railway network data have different levels of security risks. In order to improve the risk assessment mechanism for railway network data, this paper designed a risk level classification method for railway network data based on GMM clustering. The paper extracted key information from the perspectives of data and risk, and constructs a risk information dataset, obtained initial cluster centers through K-means clustering, performed GMM clustering based on mixed distance calculation, and implemented data risk level classification. Through experimental verification, compared with traditional K-means clustering and spectral clustering algorithms, the GMM clustering algorithm has a better clustering effect on railway network data and can more accurately classify the risk level of railway network data, which provide important technical support for further implementing the requirements of railway network data security management. -
随着铁路的高速发展,铁路行业已经进入了大数据时代[1];逐步成熟的大数据技术能够为铁路运输组织的各个环节予以高效指导[2-3]。铁路网络业务场景众多,数据资产规模庞大、类型繁杂、价值密度高,因此对关键信息基础设施、重要数据、个人信息、数据跨境流动等方面有较高的安全保护需求。研究并形成铁路网络数据风险等级分类方法,对落实铁路网络数据安全管理要求,确保铁路网络数据安全风险可控、在控具有重大意义。
目前,已有众多学者对风险等级分类技术进行了研究。骆公志等人[4]提出一种基于粗糙集理论的网络信息安全风险等级分类技术,通过成对比较矩阵赋予每个信息系统对应权重,生成加权多粒度粗糙集,并在模型容错性等方面进行了详细分析,但由于该方法需要拓展粗糙集模型并获取信息系统各类规则,实施过程较为复杂;陈玮等人[5]使用卷积神经网络和双向长短期记忆模型对企业新闻数据进行风险划分,但该方法需要对大量训练语料进行人工信息标注,且构建双向长短期记忆模型所花费的时间过多,实用性较差。
除上述方法外,也可使用聚类算法进行风险等级分类。李畅等人[6]基于模糊谱聚类技术,依据真实驾驶数据,建立了在线驾驶风险等级分类算法,但由于谱聚类技术对每簇数据量有一定的要求,故在数据量较大时使用受限;丁慧等人[7]使用改进的密度聚类算法进行风险等级判定,通过查询每个节点的欧氏平均距离邻域,分别计算每个节点密度和所有节点平均密度,得到每个节点的方差,并采用基于等深度分块法进行数据分割,从而在每个数据分区运行密度聚类算法,得到聚类结果。然而,该方法在对数据进行标准化处理后,使用单一距离度量方法进行聚类,没有考虑数据属性的复杂性对聚类结果带来的影响,对实际应用场景的适应性较差。
综上所述,现有的风险等级分类技术多数需要获取复杂规则或大规模信息标注,一些使用聚类方法的技术也没有考虑到数据属性的复杂性,且没有进行结果的有效性评估,进而导致无法得到最优的分类结果。
为克服现有风险等级分类方法的局限性,同时对铁路网络数据进行更加有效的风险等级分类,本文提出了基于高斯混合模型(GMM,Gaussian Mixture Model)聚类的铁路网络数据风险等级分类方法。该方法考虑数据的无序和有序属性,基于混合距离计算进行GMM聚类,最终能够将输入的数据根据其等级和生命周期阶段进行更加准确、有效的风险等级分类。本文算法以铁路数据分类分级结果为基础,识别数据在全生命周期内的潜在风险,研究并确定铁路网络数据风险等级分类,为制定差异化的数据安全保护措施提供支撑,对进一步落实铁路网络数据安全管理要求具有重大意义。
1 相关技术介绍
1.1 K-means聚类
K-means聚类算法是一种迭代求解的聚类分析算法,算法步骤如下。
(1)确定簇数和最大迭代次数,初始化类簇。
(2)初始化聚类中心。从数据样本中,随机选取k个数据样本点作为聚类中心。
(3)将数据样本分配到与其欧式距离最近的类中。
(4)迭代聚类中心。计算每个簇中所有数据样本点的均值,作为新的聚类中心。
(5)如果聚类中心不再偏移或偏移很小,或者达到最大迭代次数N,则停止迭代,输出聚类结果,否则重复步骤(3)和(4)。
1.2 距离度量
考虑到铁路网络数据属性较为复杂等特点,本文对有序属性和无序属性使用多种距离计算方式进行度量。
1.2.1 VDM距离
VDM(Value Difference Metric)主要用于对不存在序关系的离散无序数据属性进行距离度量。令
mu,a 表示在属性u上取值为a的样本数,mu,a,i 表示在第i个样本簇中在属性u上取值为a的样本数,k为样本簇个数,则属性u上两个离散值a和b之间的VDM距离为VDM2(a,b)=k∑i=1|mu,a,imu,a−mu,b,imu,b|2 (1) 1.2.2 MindkovDM混合距离
对于有序属性和无序属性同时存在的混合距离计算,本文采用MindkovDM距离计算方法,将欧式距离和VDM距离结合,假定共有n个属性,其中,
nc 个无序属性,n−nc 个有序属性,则MinkovDM距离为MinkovDM(xi,xj)=√nc∑u=1VDM2(xiu,xju)+n∑u=nc+1|xiu−xju|2 (2) 1.3 GMM聚类
根据铁路网络数据规模大、数据类型多样等特点,本文使用GMM聚类技术。对于大规模数据,GMM聚类算法相较其他聚类算法更加有效,且时间复杂度更低[8],聚类结果也更加稳定。与K-means聚类方法不同,这种聚类方法依概率划分各个样本簇,而不会将数据确定地分为某一个簇。该方法采用的训练模型是几个高斯模型的加权和,之后将样本数据分别在若干个高斯模型上进行投影,分别得到这些样本数据点被划分在各个类簇上的概率,最后选取概率最大的簇作为数据点最终划分结果[9]。
2 铁路网络数据风险分类算法
铁路网络数据风险分类步骤为:(1)数据预处理,从风险和数据角度提取关键信息,构建风险信息数据集;(2)利用数据的有序属性进行K-means聚类,获得初始聚类中心;(3)通过计算混合距离调整聚类中心;(4)基于上述聚类中心,进行多轮迭代,完成GMM聚类,并对每轮聚类结果进行评估;(5)将评估表现最好的聚类结果作为最终类簇划分,并确定每类风险评分,最终根据评分确定风险等级,完成数据风险等级分类,如图1所示。
2.1 数据预处理
对铁路网络数据进行预处理,根据铁路网络数据风险评估指标,从风险和数据角度提取关键信息。从数据角度,以铁路网络数据分类分级要求作为基础依据,提取不同级别数据的关键信息,包括数据等级、数据在全生命周期中所处不同阶段,形成数据信息;从风险角度,对现有数据风险进行分析,获取数据生命周期不同阶段面临的风险类型、风险影响程度,形成统一的风险信息。将以上2方面信息构成数据风险信息并存入风险信息数据库,数据自身属性与风险属性联合作为辅助数据风险等级分类的属性。上述过程获取的数据属性被分为2类,即有序属性和无序属性。有序属性:能直接在属性值上计算距离的属性,如{1,2,3}。无序属性:不能直接在属性值上计算距离的属性,如{小狗,小猫,老鼠}。
2.2 通过K-means聚类获得初始聚类中心
在对数据进行预处理后,使用数据中的有序属性进行K-means聚类操作得到初始的聚类中心和聚类结果,为每个数据样本分配初始标签,方便后续利用混合属性对聚类中心进行调整。
2.3 通过计算混合距离调整聚类中心
利用欧式距离计算方法对有序属性间的距离进行计算,利用VDM距离计算方法和步骤(2)中得到的数据标签对无序属性间的距离进行计算。随后使用MindkovDM混合距离计算方法聚合计算得出混合距离,实施基于混合距离的K-means再聚类,得到每个类簇的簇中心。
2.4 GMM聚类与评估
将步骤(3)中得到的聚类中心作为GMM聚类算法的初始中心,使用最大似然函数确定每个数据样本属于哪个高斯分布;使用最大期望(EM,Expectation Maximization)算法求解GMM参数[10],更新所有高斯分布的均值和方差;计算模型的似然函数,使用似然函数判断模型参数是否已经收敛;迭代更新模型参数,直至收敛,即完成一次聚类过程。设置多个轮次进行上述聚类过程,计算聚类结果的紧密性(CP)与分离性(SP),其中,CP表示每一个类中各数据点到聚类中心的平均距离,CP值越低表明类内数据点间距离越近;SP表示各聚类中心两两之间距离之和的平均值,SP值越高表明类间距离越远。该步骤将CP值与SP值的比值作为每次聚类的评价指标,规定轮次的聚类结束后,将比值最小的聚类结果作为最终的聚类划分(即风险划分)结果。
2.5 计算风险评分确定风险等级
假设每个样本面临m个数据风险,则每个样本的风险分数计算公式为
样本风险分=数据等级×α+数据风险影响程度×(1−α) (3) 数据风险影响程度=m∑i=1该样本面临的第 i 个数据风险影响程度值 (4) 其中,
α 用来平衡数据等级与数据风险影响程度对最终风险值的影响占比,由于数据等级的高低也是影响数据潜在风险危害程度的重要因素,故通常0.5⩽ ;数据风险影响程度值由输入的数据风险表提供。利用风险等级计算公式,根据每一类簇中的数据样本的有序属性的属性值计算评分,得到最终的风险等级分类。假设某一类簇中有m个样本,则这一类的风险总分计算公式为
类风险总分=\frac{1}{m}\sum\limits_{i=1}^m样本\ i\ 风险分 (5) 对于每一个类簇,计算出的风险分数越高,表示该类包含的数据潜在的风险越大,风险等级越高。
3 实验与分析
对提出的数据风险等级分类方法进行实验评估:收集铁路网络数据作为实验数据集,将本文提出的GMM聚类算法和传统K-means聚类、谱聚类算法进行结果的直观对比与分析;通过比较上述算法在轮廓系数[11]、CH(Calinski-Harabasz)分数、戴维森堡丁指数(DBI)[12]等评价指标上的表现,进一步评估聚类效果。
3.1 数据集
本文收集铁路网络数据,并对其进行预处理,根据铁路网络数据风险评估指标从风险和数据角度提取关键信息。
从数据角度,提取数据等级、数据在全生命周期中所处不同阶段,形成数据信息,按照数据的重要程度将数据划分为一般数据、重要数据和核心数据,此外,将一般数据划分为4级,由S1~S4表示。数据等级由低到高表示为0~5。如表1所示。
表 1 数据等级核心数据 重要数据 一般数据 S1 S2 S3 S4 5 4 3 2 1 0 从风险角度,获取数据生命周期不同阶段面临的风险类型及风险影响程度,分别如表2、表3所示。
表 2 数据生命周期及相应风险类型恶意代码注入 数据分类分级或标记错误 数据不可控 数据未脱敏 数据窃取 数据监听 数据篡改 数据到期未销毁 数据采集 √ √ 数据传输 √ √ √ 数据存储 √ √ √ √ 数据共享 √ √ 数据处理 √ √ 数据销毁 √ 表 3 风险影响程度等级 标识 定义 5 很高 若风险发生,将对资产造成特别重大损害 4 高 若风险发生,将对资产造成重大损害 3 中等 若风险发生,将对资产造成一般损害 2 低 若风险发生,将对资产造成较小损害 1 很低 若风险发生,对资产造成的损害可以忽略 将从以上2方面提取的信息联合作为辅助数据风险等级分类的属性,构建数据集。
3.2 评价指标
3.2.1 轮廓系数
对于单个样本,设a是与它同类别中其他样本的平均距离,b是与它距离最近的不同类别中样本的平均距离,则其轮廓系数为
s = \frac{{b - a}}{{\max (a,b)}} (6) 一个样本簇的轮廓系数取值范围为[−1,1],轮廓系数越高,聚类效果越好。
3.2.2 CH分数
CH分数通过计算类中各点与类中心的距离平方和来度量类内的紧密度,通过计算各类中心点与数据集中心点距离平方和来度量数据集的分离度,CH指标由分离度与紧密度的比值得到。取值范围为[0,+∞),CH分数越大,聚类效果越好。
3.2.3 DBI指数
DBI指数又称为分类适确性指标,取值范围为[0,+∞),该指数越小,聚类效果越好,计算公式为
DBI = \frac{1}{N}\sum\limits_{i = 1}^N {\mathop {\max }\limits_{j \ne i} } \frac{{\overline {{S_i}} + \overline {{S_j}} }}{{{{\left\| {{w_i} - \left. {{w_j}} \right\|} \right.}_2}}} (7) 其中,
\overline{S\mathit{_{{i}}}} 为第i类样本到其类中心的平均欧氏距离;\left\| {{w_i}} \right. - {\left. {{w_j}} \right\|_2} 为第i和第j类的类中心欧氏距离。3.3 实验结果分析
3.3.1 GMM聚类结果及分析
通过GMM聚类算法将数据集划分为5类,根据每类的风险分值进行风险等级划分,分数越高,风险越大。风险等级由低到高分为I级、II级、III级、IV级、V级。为获得最好的聚类结果,设置多个迭代次数进行GMM聚类,将CP和SP的比值作为评价指标,对每次聚类结果进行评估,确保聚类结果可靠,多轮聚类结束后,将比值最小的聚类结果作为最终的聚类划分结果。聚类结果如图2所示。
3.3.2 K-means聚类结果及分析
只考虑有序属性的K-means聚类算法及考虑混合属性的K-means聚类算法所得的聚类结果分别如图3、图4所示。根据实验结果,可以得出无论是否考虑数据的混合属性,传统K-means聚类结果对类簇的划分界限均不清晰,各个类簇之间的重叠情况较为严重。
3.3.3 谱聚类结果及分析
采用谱聚类算法所得聚类结果如图5所示,该方法无法产生正确的聚类划分结果,聚类中心偏移严重,聚类数据点划分类别不明确。
综上,通过聚类结果的直观对比,本文所提方法比传统K-means聚类方法及谱聚类方法更有效,产生的风险划分结果更加明确清晰。
3.3.4 各聚类算法评估指标对比
除通过聚类结果直接进行上述对比,本文还使用轮廓系数、CH分数、DBI指数这3个聚类效果评估指标,对以上4种聚类结果进行分析。评估指标计算结果如表4所示。
表 4 各种算法聚类效果评估指标GMM算法
(本文算法)只考虑有序属性的
K-means算法考虑混合属性的
K-means算法谱聚类算法 轮廓系数 0.313 0.218 0.129 −0.298 CH分数 461.35073 522.46201 387.90735 163.54651 DBI指数 1.38777 4.63512 5.41175 4.17126 根据3.2节可知,轮廓系数越高,CH分数越大,DBI指数越小,聚类效果越好。由表4可知,本文提出的GMM算法在轮廓系数上计算结果最高,在CH分数上高于考虑混合属性的K-means算法和谱聚类算法,在DBI指数上明显低于其他3种算法。综上,使用本文提出的聚类算法所得到的聚类效果明显优于其余聚类算法的聚类效果。
3.4 风险等级划分结果
根据3.3节所得聚类结果,按照公式(3)~(5)给出的风险值计算公式,将铁路数据划分为5个风险等级,如表5所示。
表 5 数据风险等级划分结果等级 风险类型 风险值 描述 V 高风险 21.40 如果数据被损害,将造成特别重大危害 IV 高风险 20.59 如果数据被损害,将造成重大危害 III 中风险 14.10 如果数据被损害,将造成一般危害 II 中风险 9.78 如果数据被损害,将造成较小危害 I 低风险 7.23 如果数据被损害,将造成的危害可以忽略 4 结束语
本文设计了一种基于GMM聚类的铁路网络数据风险等级分类方法,使用K-means和GMM聚类技术对铁路网络数据进行多阶段聚类。实验结果表明,本文提出的方法解决了具有混合属性数据的类别划分问题和聚类算法随机初始化带来的聚类结果随机性问题,能够更加准确地对铁路网络数据进行风险等级分类,为完善铁路网络数据风险评估机制提供了有效的技术基础。未来将考虑对铁路网络系统中各类风险与各种数据资产之间更加复杂的关系进行联合建模,利用深度学习技术作进一步的研究。
-
表 1 数据等级
核心数据 重要数据 一般数据 S1 S2 S3 S4 5 4 3 2 1 0 表 2 数据生命周期及相应风险类型
恶意代码注入 数据分类分级或标记错误 数据不可控 数据未脱敏 数据窃取 数据监听 数据篡改 数据到期未销毁 数据采集 √ √ 数据传输 √ √ √ 数据存储 √ √ √ √ 数据共享 √ √ 数据处理 √ √ 数据销毁 √ 表 3 风险影响程度
等级 标识 定义 5 很高 若风险发生,将对资产造成特别重大损害 4 高 若风险发生,将对资产造成重大损害 3 中等 若风险发生,将对资产造成一般损害 2 低 若风险发生,将对资产造成较小损害 1 很低 若风险发生,对资产造成的损害可以忽略 表 4 各种算法聚类效果评估指标
GMM算法
(本文算法)只考虑有序属性的
K-means算法考虑混合属性的
K-means算法谱聚类算法 轮廓系数 0.313 0.218 0.129 −0.298 CH分数 461.35073 522.46201 387.90735 163.54651 DBI指数 1.38777 4.63512 5.41175 4.17126 表 5 数据风险等级划分结果
等级 风险类型 风险值 描述 V 高风险 21.40 如果数据被损害,将造成特别重大危害 IV 高风险 20.59 如果数据被损害,将造成重大危害 III 中风险 14.10 如果数据被损害,将造成一般危害 II 中风险 9.78 如果数据被损害,将造成较小危害 I 低风险 7.23 如果数据被损害,将造成的危害可以忽略 -
[1] 王 喆. 铁路大数据治理体系研究[J]. 网络安全与数据治理,2022,41(11):30-35. [2] 司 瑜. 大数据在铁路运输组织工作中的应用[J]. 科技创新与应用,2019,9(14):178-179. [3] 马小宁. 铁路大数据应用实践及展望[J]. 铁路计算机应用,2019,28(4):8-13. DOI: 10.3969/j.issn.1005-8451.2019.04.003 [4] 骆公志,陈圣瑜. 基于粗糙集理论的网络信息安全风险等级分类方法[J]. 计算机时代,2022(9):36-40,48. [5] 陈 玮,刘德彬,孙世通,等. 结合深度学习和逻辑规则的企业新闻数据风险分类方法:中国109472470A[P]. 2019-03-15. [6] 李 畅,孙海明,宋 攀. 乘用车谱聚类FCAS/PCW风险等级分类算法研究[J]. 湖北汽车工业学院学报,2020,34(1):32-38. DOI: 10.3969/j.issn.1008-5483.2020.01.008 [7] 丁 慧,陈湘华,陈大伟,等. 一种基于数据信息挖掘技术的火灾防控方法:中国109472470A[P]. 2023-06-30. [8] 王凯南,金立左. 基于高斯混合模型的EM算法改进与优化[J]. 工业控制计算机,2017,30(5):115-116,118. DOI: 10.3969/j.issn.1001-182X.2017.05.049 [9] Celeux G, Govaert G. Gaussian parsimonious clustering models[J]. Pattern Recognition, 1995, 28(5): 781-793. DOI: 10.1016/0031-3203(94)00125-6
[10] Balakrishnan S, Wainwright M J, Yu B. Statistical guarantees for the EM algorithm: from population to sample-based analysis[J]. The Annals of Statistics, 2017, 45(1): 77-120.
[11] 朱连江,马炳先,赵学泉. 基于轮廓系数的聚类有效性分析[J]. 计算机应用,2010,30(S2):139-141,198. [12] Davies D L, Bouldin D W. A cluster separation measure[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1979, PAMI-1(2): 224-272. DOI: 10.1109/TPAMI.1979.4766909
-
期刊类型引用(1)
1. 张渊. 基于数据治理技术的铁路站区协同作业研究与应用. 运输经理世界. 2024(18): 163-165 .  百度学术
百度学术
其他类型引用(3)




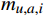
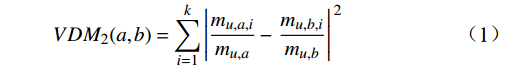
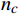
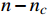
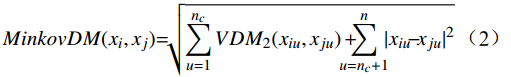

 下载:
下载: