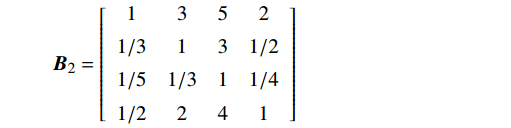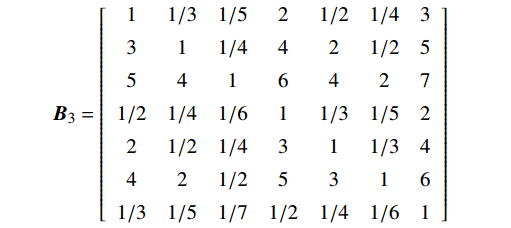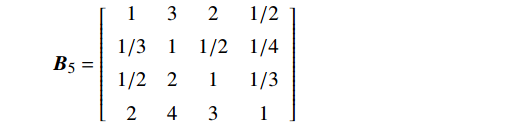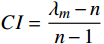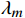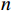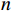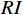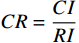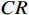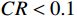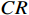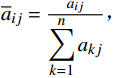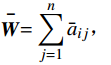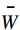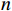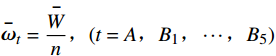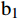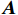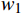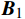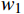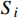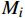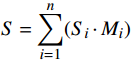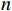Evaluation method of railway network security inspection based on Analytic Hierarchy Process
-
摘要: 网络安全检查指标及评价是目前铁路主流的监督检查方式,是促进安全策略决策制定的重要措施。文章分析故障树分析法、神经网络法的适用范围和局限性,提出基于层次分析法的铁路网络安全检查评价方法,分层次设置网络安全检查指标,设置指标权重,并开展检查实例验证。研究结果可为后续铁路网络安全年度检查工作提供技术参考依据。Abstract: Network security inspection indicators and evaluation are currently the mainstream supervision and inspection methods in railways, and are important measures to promote the formulation of security strategy decisions. This paper analyzed the applicability and limitations of fault tree analysis and neural network methods, proposed an evaluation method of railway network security inspection based on Analytic Hierarchy Process, set network security inspection indicators and indicator weights in different levels, and conducted inspection case validation. The research results can provide technical reference for the subsequent annual inspection of railway network security.
-
Keywords:
- Analytic Hierarchy Process /
- network security /
- inspection indicators /
- weight /
- evaluation
-
随着信息化的发展,网络技术在各行各业得到了广泛应用,随之而来的是愈发严峻的安全隐患。国际上针对他国的网络安全攻击日趋激烈,给国家安全造成重大威胁,保护国家网络安全已成为国际社会关注的焦点。基于上述情况,迫切需要针对铁路网络安全检查工作开展研究,为保障铁路关键信息基础设施稳定运行创造必要条件。
现有网络安全检查方法有很多,包括故障树分析法( FTA,Fault Tree Analysis)[1-3]、卷积神经网络(CNN,Convolutional Neural Network)[4-6]、层次分析法(AHP,Analytic Hierarchy Process)等[7-10]。安慧等人[3]将故障树分析法运用在建筑施工风险评估中,分析高处坠落事故的相关风险及后果,该方法以事故为起始,通过因果关系逐层分析,其优势在于能够分析出事故发生的直接原因,但其分析过程中的专家评判需要耗费大量人力和时间,且其指标权重具有一定的概率数据偏差;颜蔚[5]采用基于卷积神经网络模型的无线网络安全风险评估方法评估无线网络安全风险,以提高其评估准确性,其优势在于对于已训练的模型能够较快分析得到较为精准的结果,但其劣势在于训练过程需要大量数据资源,且对位置和尺度敏感,当评判指标发生改变后需要重新耗费大量资源训练其权重;郭琳等人[7]利用AHP计算网络态势评估中攻击类型的影响权重,分别通过对准则层和指标层构建判断矩阵以计算各指标的最终权重,相比之下,通过该方法进行网络安全检查分析可以较好地规避上述2种方法存在的问题。
鉴于此,本文结合相关要求及行业标准,提出基于层次分析法的铁路网络安全检查评价方法。构建以组织制度保障、网络安全测评、安全运营维护(简称:运维)、供应链安全和数据安全为框架的3级铁路网络安全检查指标体系,并基于AHP计算各指标权限,最终实现定量定性的铁路网络安全风险评价。
1 铁路网络安全检查指标体系构建
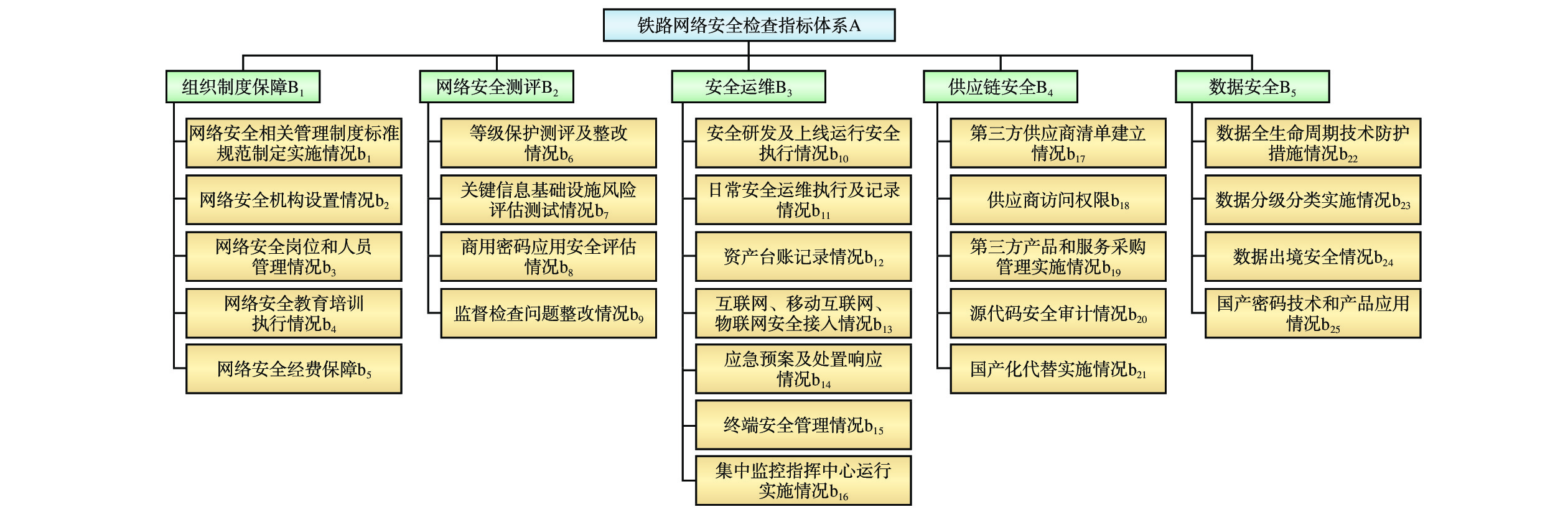
通过对组织制度保障、网络安全测评、安全运维、供应链安全和数据安全等5个层面网络安全检查指标的进一步细化,提出3级铁路网络安全检查指标体系,如图1所示。
(1)组织制度保障(B1)。主要包括:网络安全相关管理制度标准规范制定实施情况(b1),检查是否结合目标单位或系统的实际情况,制定网络安全标准或制度;网络安全机构设置情况(b2),检查目标单位或部门是否设置相应的网络安全机构;网络安全岗位和人员管理情况(b3),检查目标单位是否存在网络安全相关岗位及人员;网络安全教育培训执行情况(b4),检查是否定期进行网络安全教育的培训;网络安全经费保障(b5),检查单位或部门为网络安全经费投入的占比。
(2)网络安全测评(B2)。主要包括:等级保护测评及整改情况(b6),检查目标系统是否经过等级保护测评,相关单位及部门是否根据报告及时进行整改;关键信息基础设施风险评估测试情况(b7),检查相关系统是否经过风险评估测试,测试结果是否符合规定;商用密码应用安全评估情况(b8),检查应用商用密码是否符合相关安全规定;监督检查问题整改情况(b9),检查是否有专项人员监督整改,检查问题是否已整改完善。
(3)安全运维(B3)。主要包括:安全研发及上线运行安全执行情况(b10),检查系统软件研发和运行阶段是否处于安全环境;日常安全运维执行及记录情况(b11),是否存在系统软件安全检查记录,检查记录各项结果是否符合规定;资产台账记录情况(b12),检查目标单位中各资产是否记录在台账中;互联网、移动互联网、物联网安全接入情况(b13),检查目标单位是否按照安全规定进行互联网准入;应急预案及处置响应情况(b14),检查目标单位面对应急情况是否存在相应合理的预案,是否能及时进行响应;终端安全管理情况(b15),检查是否定期对单位内终端机器进行管理;集中监控指挥中心运行实施情况(b16),检查单位指挥中心是否能进行全方位监控,是否能对目标部门及时进行任务调度指挥控制。
(4)供应链安全(B4)。主要包括:第三方供应商清单建立情况(b17),检查是否对供应商建立产品的详细清单;供应商访问权限(b18),检查供应商在目标系统上所掌握的访问权限;第三方产品和服务采购管理实施情况(b19),检查是否部署相关制度以管理第三方产品及服务;源代码安全审计情况(b20),检查是否能对第三方软件或系统的开源代码进行审计;国产化代替实施情况(b21),检查当前使用国产化产品的占比。
(5)数据安全(B5)。主要包括:数据全生命周期技术防护措施情况(b22),检查是否基于数据全生命周期部署相应的防护措施;数据分级分类(b23),检查数据是否进行分级分类;数据出境安全情况(b24),检查运行数据是否存在出境情况,出入境数据是否进行隔离和检查;国产密码技术和产品应用情况(b25),检查单位及系统是否应用国产密码技术及产品。
2 铁路网络安全检查评价方法
基于上述铁路网络安全检查指标,引入AHP进行分析。AHP是一种结合定性定量的综合风险评估分析方法,其原理是按照一定关系将各种判断因素分层分解为目标层、准则层和指标层,再将各因素之间的差异数值化并赋予不同重要性权重,最终适用于复杂系统的检查评价。
为实现对铁路网络的安全检查,将安全检查指标体系作为目标层,5项安全检查内容作为准则层,相对应的25项检查指标作为指标层,对每项检查指标制定计算方法,从而建立铁路网络安全检查指标体系,实现基于AHP的风险评价模型。在对各单位系统检查时,检查人员依据各指标的具体实施完成情况进行打分(0~100分),再结合各指标的权重计算系统最终的风险评价值。
为计算各指标的权重,邀请10位来自高校、科研院所和生产单位的专家对两两指标间的重要性程度进行比较打分,其判断尺度如表1所示。若因素i与因素j 的重要性之比为aij,则因素 j 与因素i的重要性之比为aji=1/aij。
表 1 指标间重要性程度分值判断尺度分值 含义 1 两个因素比较具有相同重要性 3 前一因素比后一因素稍微重要 5 前一因素比后一因素明显重要 7 前一因素比后一因素强烈重要 9 前一因素比后一因素绝对重要 2,4,6,8 表示上述相邻判断的中间值 2.1 构造判断矩阵
基于专家意见,结合准则层5项准则之间的重要性判断分值,构建目标层铁路网络安全检查指标体系A的比较判断矩阵A,如下所示
{{\boldsymbol{A}}}=\left[\begin{array}{ccccc}1& 3& 5& 4& 2\\ 1/3& 1& 3& 2& 1/2\\ 1/5& 1/3& 1& 1/2& 1/4\\ 1/4& 1/2& 2& 1& 1/3\\ 1/2& 2& 4& 3& 1\end{array}\right] 通过同样的方法比较指标层中各项指标间的重要性分值,构造出B1~B5的比较判断矩阵B1~B5。
{\boldsymbol{B}}_{1}=\left[\begin{array}{ccccc}1& 4& 6& 7& 2\\ 1/4& 1& 3& 4& 1/3\\ 1/6& 1/3& 1& 2& 1/5\\ 1/7& 1/4& 1/2& 1& 1/6\\ 1/2& 3& 5& 6& 1\end{array}\right] {\boldsymbol{B}}_{2}=\left[\begin{array}{cccc}1& 3& 5& 2\\ 1/3& 1& 3& 1/2\\ 1/5& 1/3& 1& 1/4\\ 1/2& 2& 4& 1\end{array}\right] {\boldsymbol{B}}_{3}=\left[\begin{array}{ccccccc}1& 1/3& 1/5& 2& 1/2& 1/4& 3\\ 3& 1& 1/4& 4& 2& 1/2& 5\\ 5& 4& 1& 6& 4& 2& 7\\ 1/2& 1/4& 1/6& 1& 1/3& 1/5& 2\\ 2& 1/2& 1/4& 3& 1& 1/3& 4\\ 4& 2& 1/2& 5& 3& 1& 6\\ 1/3& 1/5& 1/7& 1/2& 1/4& 1/6& 1\end{array}\right] {\boldsymbol{B}}_{4}=\left[\begin{array}{ccccc}1& 2& 1/2& 1/4& 4\\ 1/2& 1& 1/3& 1/5& 3\\ 2& 3& 1& 1/3& 5\\ 4& 5& 3& 1& 7\\ 1/4& 1/3& 1/5& 1/7& 1\end{array}\right] {\boldsymbol{B}}_{5}=\left[\begin{array}{cccc}1& 3& 2& 1/2\\ 1/3& 1& 1/2& 1/4\\ 1/2& 2& 1& 1/3\\ 2& 4& 3& 1\end{array}\right] 2.2 矩阵的一致性检验
考虑到在建立判断矩阵时存在大量的专家主观经验,为清除由于主观性而导致的明显逻辑错误,需要先对矩阵进行一致性检验。
矩阵一致性指标
CI=\dfrac{{\lambda }_{m}-n}{n-1} ,其中:{\lambda }_{m} 为矩阵最大特征值,n 为矩阵阶数。再根据矩阵阶数n 查询其对应的平均随机一致性指标RI ,并计算矩阵一致性比率CR=\dfrac{CI}{RI} ,CR 的值越小说明矩阵一致性越好,一般认为当CR < 0.1 时矩阵一致性可以接受。经过计算,上文中判断矩阵的
CR 值分别为:0.0205, 0.0205, 0.0194, 0.0578, 0.0416, 0.0117,均小于0.1,通过了一致性检验,确保了矩阵构建的合理性。2.3 计算各判断矩阵权重向量
为确定各准则及指标间的权重值,需要先对判断矩阵使用算术平均法进行归一化处理,其步骤如下。
(1)将矩阵每一列进行向量归一化:
\overline{a}_{ij}=\frac{a_{ij}}{\displaystyle\sum_{k=1}^na_{kj}}, (i={1,2},\cdots,\ n) ;(2)对归一化后的矩阵进行按行求和:
\stackrel{-}{{\boldsymbol{W}}}=\displaystyle \sum _{j=1}^{n}{{\bar a}_{ij}}, (i=\mathrm{1,2},\cdots,n) ;(3)将向量
\stackrel{-}{W} 除以判断矩阵阶数n 得到各元素权重向量:{\stackrel{-}{\boldsymbol{\omega}}}_{t}=\dfrac{\stackrel{-}{W}}{n},(t={A},{{B}}_{1},\cdots ,{{B}}_{5}) 。各矩阵的权重向量以及一致性检验结果如表2所示。
表 2 各矩阵的权重向量以及一致性检验结果判断矩阵 {w}_{1} {w}_{2} {w}_{3} {w}_{4} {w}_{5} {w}_{6} {w}_{7} {\lambda }_{m} CR { {\boldsymbol{A} } } 0.4162 0.1611 0.0624 0.0986 0.2618 — — 5.0680 0.0205 {\boldsymbol{B} }_{1} 0.4458 0.1443 0.0677 0.0452 0.2970 — — 5.1990 0.0420 {\boldsymbol{B} }_{2} 0.4709 0.1715 0.0736 0.2840 — — — 4.0510 0.0194 {\boldsymbol{B} }_{3} 0.0692 0.1525 0.3624 0.0459 0.1048 0.2337 0.0316 7.2260 0.0578 {\boldsymbol{B} }_{4} 0.1469 0.0946 0.2289 0.4845 0.0451 — — 5.1380 0.0416 {\boldsymbol{B} }_{5} 0.2771 0.0960 0.1611 0.4658 — — — 4.0310 0.0117 2.4 各指标最终权重计算及分析
铁路网络安全检查指标体系的最终权重通过对应准则及指标所在权重值乘积所得(例:指标
{\mathrm{b}}_{1} 的最终权重为判断矩阵\boldsymbol{A} 中的{w}_{1} 乘判断矩阵{\boldsymbol{B}}_{1} 中的{w}_{1} ),如表3所示,其中,组织制度保障比重占检查总指标的41.85%,位于检查指标的主导地位,因此在对铁路网络安全检查时,应该结合目标单位及系统的规章制度,重点检查其是否按要求执行实施。数据安全占检查指标的26.25%,对数据全生命周期技术防护措施的部署和国产化密码技术产品的应用也是检查的重点内容。另外,网络安全测评也是不可忽视的重要环节。表 3 各指标所占总权重{{\rm{A}}} { {{\rm{B}}} }_{1} {{{\rm{B}}} }_{2} {{{\rm{B}}} }_{3} {{{\rm{B}}} }_{4} {\rm{B} }_{5} 各指标相对于总目标的权重 {M}_{i} 0.4162 0.1611 0.0624 0.0986 0.2618 {\mathrm{b}}_{1} 0.4458 — — — — 0.1855 {\mathrm{b}}_{2} 0.1443 — — — — 0.0601 {\mathrm{b}}_{3} 0.0677 — — — — 0.0282 {\mathrm{b}}_{4} 0.0452 — — — — 0.0188 {\mathrm{b}}_{5} 0.2970 — — — — 0.1236 {\mathrm{b}}_{6} — 0.4709 — — — 0.0759 {\mathrm{b}}_{7} — 0.1715 — — — 0.0276 {\mathrm{b}}_{8} — 0.0736 — — — 0.0119 {\mathrm{b}}_{9} — 0.2840 — — — 0.0458 {\mathrm{b}}_{10} — — 0.0692 — — 0.0043 {\mathrm{b}}_{11} — — 0.1525 — — 0.0095 {\mathrm{b}}_{12} — — 0.3624 — — 0.0226 {\mathrm{b}}_{13} — — 0.0459 — — 0.0029 {\mathrm{b}}_{14} — — 0.1048 — — 0.0065 {\mathrm{b}}_{15} — — 0.2337 — — 0.0146 {\mathrm{b}}_{16} — — 0.0316 — — 0.0020 {\mathrm{b}}_{17} — — — 0.1469 — 0.0145 {\mathrm{b}}_{18} — — — 0.0946 — 0.0093 {\mathrm{b}}_{19} — — — 0.2289 — 0.0226 {\mathrm{b}}_{20} — — — 0.4845 — 0.0478 {\mathrm{b}}_{21} — — — 0.0451 — 0.0044 {\mathrm{b}}_{22} — — — — 0.2771 0.0725 {\mathrm{b}}_{23} — — — — 0.0960 0.0251 {\mathrm{b}}_{24} — — — — 0.1611 0.0422 {\mathrm{b}}_{25} — — — — 0.4658 0.1219 2.5 运用AHP量化检查结果
在铁路网络安全检查过程中,根据检查指标逐项打分网络安全情况,对每一项得到的分值
{S}_{i} ,与该指标所占总权重{M}_{i} 相乘,得到该项检查指标的最终分值;通过汇总全部检查指标的分值,计算出目标网络安全检查得分S=\displaystyle\sum_{i=1}^n(S_i\cdot M_i) ,式中n 为检测指标数量。将计算的分值结合表4中的判定标准,得出最终的评价等级。表 4 网络安全检查风险判定标准风险程度 量化评价值 风险说明 低风险 S\geqslant 80 被检查系统处于较高安全状态,风险较低 中风险 80 > S\geqslant 60 被检查系统存在一定安全隐患,但风险可控 高风险 S<60 被检查系统存在较大安全隐患,应立即进行安全加固,
降低安全风险2.6 铁路网络安全检查评价指标验证
为验证本文所提方法计算权重的正确性,以铁路典型二级信息系统、三级信息系统和四级信息系统为例开展验证分析。检查人员根据本文第一章中的指标内容完成情况进行打分,再用网络安全检查得分公式计算目标系统的风险评价得分,最后根据网络安全检查风险判定标准得出目标系统的风险程度。最终结果同系统等级保护测评、风险评估等相关测评结论得出的安全防护情况相同,基本反映信息系统的实际安全风险状况,从而证实本文方法计算权重值的有效性。
3 结束语
本文构建了铁路网络安全检查指标体系,提出了一种基于AHP的综合评价方法。通过分析检查内容和检查指标的重要性计算各评价指标的权重,最终定量定性地给出目标系统风险值及评价结果,该方法对网络安全检查工作具有一定参考意义。在后续常态化网络安全检查过程中,有待进一步研究如何进行指标和权重的持续性更新,以满足铁路新的网络安全要求。
-
表 1 指标间重要性程度分值判断尺度
分值 含义 1 两个因素比较具有相同重要性 3 前一因素比后一因素稍微重要 5 前一因素比后一因素明显重要 7 前一因素比后一因素强烈重要 9 前一因素比后一因素绝对重要 2,4,6,8 表示上述相邻判断的中间值 表 2 各矩阵的权重向量以及一致性检验结果
判断矩阵 {w}_{1} {w}_{2} {w}_{3} {w}_{4} {w}_{5} {w}_{6} {w}_{7} {\lambda }_{m} CR { {\boldsymbol{A} } } 0.4162 0.1611 0.0624 0.0986 0.2618 — — 5.0680 0.0205 {\boldsymbol{B} }_{1} 0.4458 0.1443 0.0677 0.0452 0.2970 — — 5.1990 0.0420 {\boldsymbol{B} }_{2} 0.4709 0.1715 0.0736 0.2840 — — — 4.0510 0.0194 {\boldsymbol{B} }_{3} 0.0692 0.1525 0.3624 0.0459 0.1048 0.2337 0.0316 7.2260 0.0578 {\boldsymbol{B} }_{4} 0.1469 0.0946 0.2289 0.4845 0.0451 — — 5.1380 0.0416 {\boldsymbol{B} }_{5} 0.2771 0.0960 0.1611 0.4658 — — — 4.0310 0.0117 表 3 各指标所占总权重
{{\rm{A}}} { {{\rm{B}}} }_{1} {{{\rm{B}}} }_{2} {{{\rm{B}}} }_{3} {{{\rm{B}}} }_{4} {\rm{B} }_{5} 各指标相对于总目标的权重 {M}_{i} 0.4162 0.1611 0.0624 0.0986 0.2618 {\mathrm{b}}_{1} 0.4458 — — — — 0.1855 {\mathrm{b}}_{2} 0.1443 — — — — 0.0601 {\mathrm{b}}_{3} 0.0677 — — — — 0.0282 {\mathrm{b}}_{4} 0.0452 — — — — 0.0188 {\mathrm{b}}_{5} 0.2970 — — — — 0.1236 {\mathrm{b}}_{6} — 0.4709 — — — 0.0759 {\mathrm{b}}_{7} — 0.1715 — — — 0.0276 {\mathrm{b}}_{8} — 0.0736 — — — 0.0119 {\mathrm{b}}_{9} — 0.2840 — — — 0.0458 {\mathrm{b}}_{10} — — 0.0692 — — 0.0043 {\mathrm{b}}_{11} — — 0.1525 — — 0.0095 {\mathrm{b}}_{12} — — 0.3624 — — 0.0226 {\mathrm{b}}_{13} — — 0.0459 — — 0.0029 {\mathrm{b}}_{14} — — 0.1048 — — 0.0065 {\mathrm{b}}_{15} — — 0.2337 — — 0.0146 {\mathrm{b}}_{16} — — 0.0316 — — 0.0020 {\mathrm{b}}_{17} — — — 0.1469 — 0.0145 {\mathrm{b}}_{18} — — — 0.0946 — 0.0093 {\mathrm{b}}_{19} — — — 0.2289 — 0.0226 {\mathrm{b}}_{20} — — — 0.4845 — 0.0478 {\mathrm{b}}_{21} — — — 0.0451 — 0.0044 {\mathrm{b}}_{22} — — — — 0.2771 0.0725 {\mathrm{b}}_{23} — — — — 0.0960 0.0251 {\mathrm{b}}_{24} — — — — 0.1611 0.0422 {\mathrm{b}}_{25} — — — — 0.4658 0.1219 表 4 网络安全检查风险判定标准
风险程度 量化评价值 风险说明 低风险 S\geqslant 80 被检查系统处于较高安全状态,风险较低 中风险 80 > S\geqslant 60 被检查系统存在一定安全隐患,但风险可控 高风险 S<60 被检查系统存在较大安全隐患,应立即进行安全加固,
降低安全风险 -
[1] 刘子先,李 玫. 基于FTA和Bayesian网络的血液透析感染风险评估[J]. 工业工程与管理,2017,22(3):106-113. [2] 郑雷雷,宋丽华,郭 锐,等. 故障树分析法在信息安全风险评估中的应用[J]. 计算机科学,2011,38(S1):106-108,118. [3] 安 慧,黄 艾,安 敏,等. 基于模糊故障树的建筑施工高处坠落全面风险评估[J]. 科学技术与工程,2022,22(19):8568-8576. [4] 宗志栓,张逸飞,林作忠,等. 基于概率神经网络和层次分析法的硐室群施工风险评估[J/OL]. 铁道标准设计:1-8[2023-07-31]. https://kns.cnki.net/kcms2/article/abstract?v=3uoqIhG8C45S0n9fL2suRadTyEVl2pW9UrhTDCdPD64vstmS5MNifkWekQKJqmBxb3wpnuqne9f8QOV10orrkkP7v7cojlM7&;uniplatform=NZKPT. [5] 颜 蔚. 基于卷积神经网络的无线网络安全风险评估及控制[J]. 沈阳工业大学学报,2022,44(5):565-569. [6] 李嘉锋,胡玉玲,李佳旭. 基于神经网络的公共建筑应急疏散风险评估方法[J]. 消防科学与技术,2022,41(4):491-495. [7] 郭 琳,易军凯,王 浩. 基于层次分析法的工控网络态势评估研究[J/OL]. 西安理工大学学报:1-8[2023-07-31]. https://kns.cnki.net/kcms2/article/abstract?v=3uoqIhG8C45S0n9fL2suRadTyEVl2pW9UrhTDCdPD65MlKKzmekAa64drRt5c2ZUMTr9G9Nx6TPhVPZkzMedhEPCo33drJSZ&;uniplatform=NZKPT. [8] 翟化欣. 层次分析法和神经网络的电网安全评估[J]. 现代电子技术,2016,39(21):168-171. [9] 李晨旸,张晓梅,李 媛. 一种基于层次分析法的大规模信息系统风险评估方法[J]. 计算机应用与软件,2013,30(10):322-325. [10] 张 利,彭建芬,杜宇鸽,等. 信息安全风险评估的综合评估方法综述[J]. 清华大学学报(自然科学版),2012,52(10):1364-1369. -
期刊类型引用(2)
1. 赵亮,曹祎杰,雷丝萦,姚洪磊,司群. 基于组合赋权的铁路网络数据安全评估方法研究. 铁路计算机应用. 2024(10): 1-6 .  本站查看
本站查看
2. 陶侠,齐辉,楼锋锋,张广水. 基于MC-AHP模型的发电企业安全生产责任制落实评价方法. 电力安全技术. 2024(11): 5-10 .  百度学术
百度学术
其他类型引用(5)




 下载:
下载: