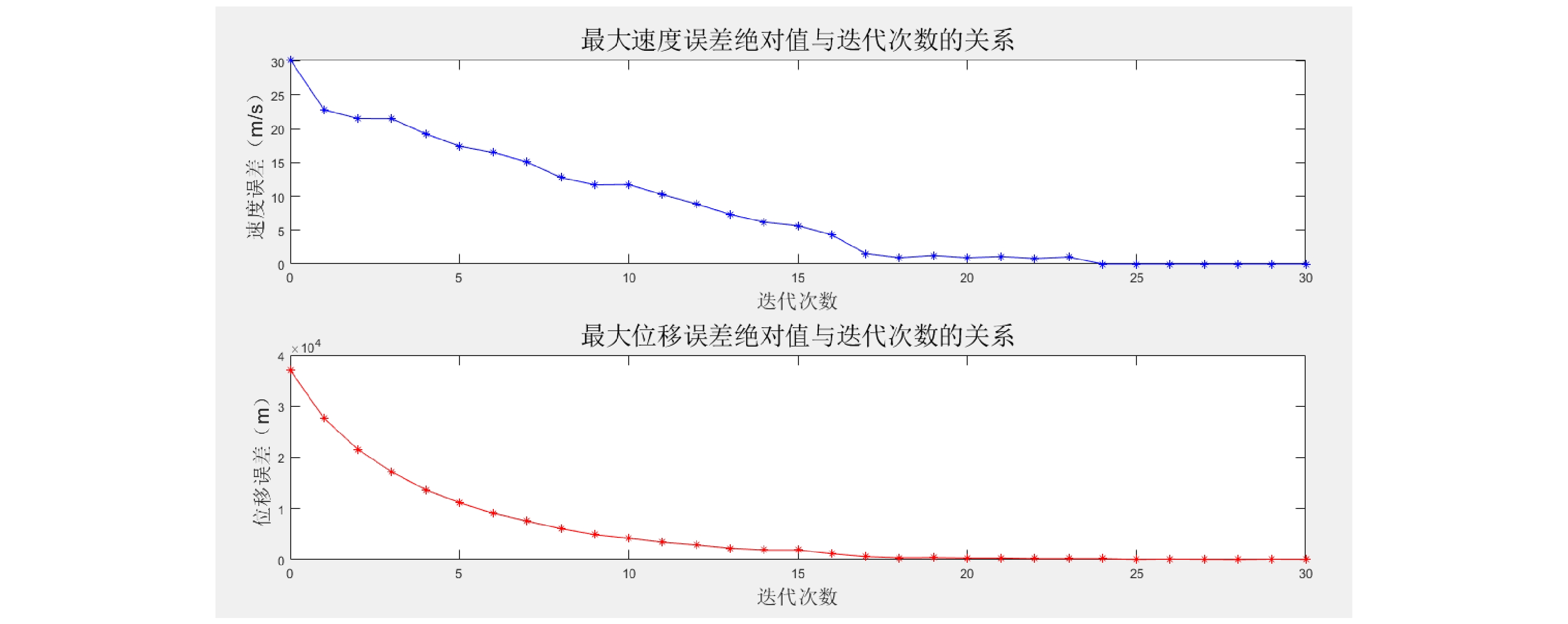
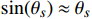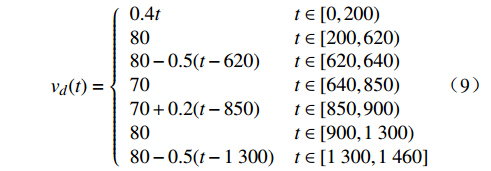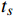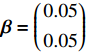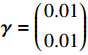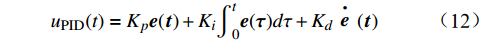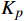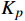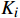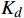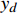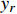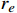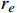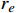Curve tracking algorithm for automatic train operation based on PID-type iterative learning control
-
摘要: 针对基于比例微分积分（PID，Proportional Integral Derivative）控制的列车速度跟踪算法在跟踪进度、收敛性和稳定性等方面存在的不足，提出一种基于PID型迭代学习控制（ILC，Iterative Learning Control）的列车自动驾驶（ATO，Automatic Train Operation）曲线跟踪算法。通过迭代学习控制，优化跟踪过程，减小跟踪误差，缩短收敛时间；设置典型场景对所设计的算法进行仿真试验，并将仿真结果与基于PID控制算法的跟踪效果进行对比分析。结果表明，PID型ILC算法对列车目标速度和目标位移具有较高的跟踪精度，能够在有限的迭代次数内实现精确跟踪，验证了所提算法的有效性。
-
关键词:
- 比例微分积分（PID） /
- 迭代学习控制（ILC） /
- 列车自动驾驶（ATO） /
- 曲线跟踪算法 /
- 跟踪误差
Abstract: To address the shortcomings of train speed tracking algorithms based on proportional integral derivative (PID) control in tracking progress, convergence, and stability, this paper oriposed a PID based iterative learning control (ILC) based automatic train operation (ATO) curve tracking algorithm. The paper optimized the tracking process through iterative learning control, reduced tracking errors, and shorten convergence time, set up typical scenarios to conduct simulation experiments on the designed algorithm, and compared and analyzed the simulation results with the tracking effect of the PID control algorithm. The results show that the PID ILC algorithm has high tracking accuracy for train target speed and target displacement, and can achieve precise tracking within a limited number of iterations, proving the effectiveness of the proposed algorithm. -
高速列车运行速度快，运行环境复杂多变，其运行控制系统易受内外部未知因素的干扰，呈现出快时变、强非线性的特征。因此，亟需设计一种智能化的列车自动驾驶（ATO，Automatic Train Operation）控制器，以保证对列车运行的精确控制。现阶段，有关ATO控制算法的研究已取得大量成果，以比例微分积分（PID，Proportional Integral Derivative）算法为代表，可将滑模控制[1]、预测控制[2-3]、模糊控制[4]、神经网络[5-6]等算法与PID相结合，用于解决列车速度自动控制精度不足、稳定性不高等问题。然而，上述方法均存在一定的局限性，如PID算法以线性近似列车速度控制中的非线性因素，无法保证控制精度；滑模控制、预测控制、模糊控制、神经网络等算法的控制规则和参数的设计与调整需要丰富的实际系统开发经验，要求较高。
高速列车在运行过程中具有重复性的特征，具体体现在列车的运行环境、运行计划、运行目标、运行工况、动力学模型、运行速度及轨迹跟踪等方面。迭代学习控制（ILC，Iterative Learning Control）是一种对以重复模式工作的系统进行跟踪控制的方法，主要适合于具有高度重复性特征的被控对象的控制器设计[7]。目前，ILC已在航空、轨道交通等领域得到了较为广泛的应用。如文献[8]采用智能PD型ILC算法解决了园区固定路段的清扫车路径跟踪问题；文献[9]提出了一种迭代控制与滑模控制相融合的策略，实现了机械臂对目标轨迹的精确跟踪；文献[10]设计了基于ILC的差分–微分参数计算律，以减小时域和迭代域上的跟踪误差；文献[11]提出了一种无模型自适应ILC容错控制策略，用于解决高速列车速度轨迹跟踪问题；文献[12]提出了一种新的ILC方案，以保证高速列车运行控制的安全性和舒适性；文献[13]提出了一种将ILC和集体更新策略相结合的集体学习控制算法，可提高系统的自主学习能力。
基于以上研究，本文提出基于PID型ILC的ATO曲线跟踪算法，以期实现对列车目标速度和目标位移的精确跟踪，并通过典型场景，仿真其跟踪精度和收敛速度，验证了算法的有效性。
1 问题概述
高速列车的运行是一个连续复杂的过程，与人、系统和环境存在紧密的关联，通常可以将该过程抽象为一个非线性的多目标优化问题。ATO系统需要具备对列车速度自动调整的功能，从而精确跟踪列车速度防护曲线，减少列车在牵引、制动和惰行等工况之间的切换，提高列车的准点率、停车精度、舒适性，降低司机的工作强度。
列车运行动力学模型是ATO系统中用于计算列车运行目标速度的基础，该模型如公式（1）～（4）所示。
$$ \frac{{dv}}{{dt}} = u - w(v) - g(s) $$ (1) $$ \frac{{ds}}{{dt}} = v $$ (2) $$ w(v) = {c_a}{v^2} + {c_v}v + {c_0} $$ (3) $$ g(s) = l \cdot \sin ({\theta _s}) $$ (4) 式中， t表示时间，s；v表示列车运行速度，m/s，
$ v\left( 0 \right) = 0 $ ；s表示列车运行距离，m，$ s\left( 0 \right) = 0 $ ；u是ATO系统作用在单位质量上的牵引力或制动力，N/kg；$ w(v) $ 表示单位质量上列车所受的基本阻力，N；$ g(s) $ 是列车所受的单位附加阻力，N；l为经验常数，通常取重力加速度；$ {\theta _s} $ 为位置s处的线路坡度，°；$ {c_a} $ 表示空气阻力常数；$ {c_v} $ 表示机械阻力常数；$ {c_0} $ 表示车轮滚动和滑动阻力常数；$ {c_a} $ 、$ {c_v} $ 、$ {c_0} $ 均为经验常数。由式（3）可知，基本阻力
$ w(v) $ 包含与列车速度的二次方相关项，具有典型的非线性特征。非线性系统的控制器设计需要尽可能保留非线性部分，以提高控制器的精度。因此，本文将PID与ILC算法相结合，在初始状态一致的情况下，可以实现对于给定的列车超速防护速度曲线的精确跟踪，当迭代次数趋于无限大时，跟踪误差可以收敛到0。2 算法设计
速度曲线追踪的控制目标是使列车运行动力学模型中的控制量（列车运行速度v和位移s）能够精确地跟踪目标速度轨迹和目标位移轨迹。因此，在设计迭代学习控制器之前，须先确定ATO系统第k次迭代时的跟踪误差。
在列车运行区间中选择一段有限的时间区间[0,T]，通常可设T为列车在两个相邻站点间的运行时间。假定列车在该区间上重复运行，将列车的运行速度v和位移s作为ATO系统的两个状态，可以将公式（1）～（4）表述为ATO系统的状态空间模型，当其迭代到第k次时，ATO系统算法为
$$ \begin{aligned} \left(\begin{array}{l}{\dot{v}}_{k}(t)\\ {\dot{s}}_{k}(t)\end{array}\right)=&\left(\begin{array}{l}-({c}_{a}{v}_{k}^{2}(t)+{c}_{v}{v}_{k}(t)+{c}_{0})-g({s}_{k}(t))\\ {v}_{k}(t)\end{array}\right)+\\ &\left(\begin{array}{l}1\\ 0\end{array}\right){{\boldsymbol{u}}}_{k}(t) \end{aligned} $$ (5) $$ {{\boldsymbol{y}}_k}(t) = \left( \begin{gathered} {v_k}(t) \\ {s_k}(t) \\ \end{gathered} \right) $$ (6) 式中，t为时间变量，s；
$ {v_k}(t) $ 为第k次迭代的列车运行速度，m/s；$ {s_k}(t) $ 为第k次迭代的列车运行位移，m；$ {\dot{v}}_{k}(t) $ 和$ {\dot{s}}_{k}(t) $ 分别为速度和位移的一阶导数，表示速度和位移的变化率；$ {{\boldsymbol{u}}_k}(t) $ 为ATO系统控制输入量，即ATO系统作用在单位质量上的牵引力或制动力；$ {{\boldsymbol{y}}_k}(t) $ 为ATO系统输出。将系统的跟踪误差
$ {{\boldsymbol{e}}_k}(t) $ 定义为$$ {{\boldsymbol{e}}_k}(t) = \left( \begin{gathered} {e_{k,1}}(t) \\ {e_{k,2}}(t) \\ \end{gathered} \right) = \left( \begin{gathered} {v_k}(t) - {v_d}(t) \\ {s_k}(t) - {s_d}(t) \\ \end{gathered} \right) $$ (7) 式中，
${{{e}}_{k,1}}(t)$ 为速度跟踪误差，m/s；$ {e_{k,2}}(t) $ 为位移跟踪误差，m；$ {v_d}(t) $ 为目标速度，m/s；$ {s_d}(t) $ 为目标位移，m。基于ILC的理念，设计迭代学习控制律公式为
$$ {{\boldsymbol{u}}}_{k+1}(t)={{\boldsymbol{u}}}_{k}(t)+\alpha {{\boldsymbol{e}}}_{k}(t)+\beta {\dot{{\boldsymbol{e}}}}_{k}(t)+\gamma {\displaystyle {\int }_{0}^{t}{{\boldsymbol{e}}}_{k}(\tau )}d\tau $$ (8) 式中，
${\boldsymbol{\alpha}} = \left( \begin{gathered} {\alpha _1} \\ {\alpha _2} \\ \end{gathered} \right)$ 为关于误差$ {{\boldsymbol{e}}_k}(t) $ 的迭代学习增益；${\boldsymbol{\beta}} = \left( \begin{gathered} {\beta _1} \\ {\beta _2} \\ \end{gathered} \right)$ 为误差变化率$ {\dot{{\boldsymbol{e}}}}_{k}(t) $ 的迭代学习增益；${\boldsymbol{\gamma}} = \left( \begin{gathered} {\gamma _1} \\ {\gamma _2} \\ \end{gathered} \right)$ 为误差积分项$ \int_0^t {{{\boldsymbol{e}}_k}(\tau )} d\tau $ 的学习律。通过在该控制器的迭代学习律中加入误差变化率和误差积分项，使得ATO系统在多次迭代之后可实现列车运行轨迹的精确跟踪。3 仿真与分析
通过典型场景对本文提出的PID型ILC算法进行仿真，并将仿真结果与PID控制结果进行对比分析，进而验证本文算法的有效性。
3.1 控制器搭建
本次仿真在Matlab（2018b）软件环境下进行。公式（3）中的运行阻力参数
$ {c_a} $ 、$ {c_v} $ 、$ {c_0} $ 均为随列车动态运行和外界环境变化的未知时变参数，在ATO系统控制器设计时通常采用经验常数。本文采用实际运营的高速铁路CRH-3型动车组部分技术参数作为仿真场景中的列车参数，如表1所示。表 1 高速铁路CRH-3型动车组部分技术参数参数 取值 编组长度 200.67 m 编组重量 380 t $ {c_a} $ 0.0166 N·h2/(km2·t) $ {c_v} $ 0.228 N·h/(km·t) $ {c_0} $ 7.75 N/t 最高运营速度 350 km/h 平均起动加速度 0.38 m/s2 3.2 仿真环境设计
列车的运行仿真线路及其参数设置如下：
（1）仿真中的线路总长为99.95 km，线路中的最大坡度为10‰，坡道长度为12.85 km，此外还包括一段坡度为7‰、长度为4.1 km的线路，仿真线路及其参数如图1所示。
由于公式（4）中的
$ {\theta _s} $ 通常为千分率级，因此，可认为$ \sin ({\theta _s}) \approx {\theta _s} $ ，取经验值l为标准重力加速度9.8 m/s2，将图1中的坡度数据代入公式（4）可得到坡度附加阻力。（2）列车在仿真线路上运行需要有时刻表的约束，仿真运行时间T为1460 s，列车在[0，T]内运行的目标速度曲线公式为
$$ {v_d}(t) = \left\{ {\begin{array}{*{20}{l}} {0.4t}&{t \in [0,200)} \\ {80}&{t \in [200,620)} \\ {80 - 0.5(t - 620)}&{t \in [620,640)} \\ {70}&{t \in [640,850)} \\ {70 + 0.2(t - 850)}&{t \in [850,900)} \\ {80}&{t \in [900,1\;300)} \\ {80 - 0.5(t - 1\;300)}&{t \in [1\;300,1\;460]} \end{array}} \right. $$ (9) 列车在[0，T]内的目标位移轨公式为
$$ {s_d}(t) = \left\{ {\begin{array}{*{20}{l}} {0.2{t^2}}&{ t \in [0,200)} \\ {8\;000 + 80(t - 200)}&{ t \in [200,620)} \\ 41\;600 - 0.25{{(t - 620)}^2} + \\80(t - 620)&{ t \in [620,640)} \\ {43\;100 + 70(t - 640)}&{ t \in [640,850)} \\ 57\;800 + 0.1{{(t - 850)}^2} + \\70(t - 850)&{ t \in [850,900)} \\ {61\;550 + 80(t - 900)}&{ t \in [900,1\;300)} \\ 93\;550 - 0.25{{(t - 1\;300)}^2} +\\ 80(t - 1\;300)&{ t \in [1\;300,1\;460]} \end{array}} \right. $$ (10) （3）本文设计的ILC算法是基于迭代域和时间域的，其中，反馈控制是在时间域上实现的；迭代学习控制是在迭代域上实现的。为保证仿真过程中的数据采样精度，将采样时间
$ {t_s} $ 设置为0.1 s。（4）经过反复试验，选取迭代学习增益
${\boldsymbol{\alpha}} = \left( \begin{gathered} 0.5 \\ 0.5 \\ \end{gathered} \right)$ ，${\boldsymbol{\beta}} = \left( \begin{gathered} 0.05 \\ 0.05 \\ \end{gathered} \right)$ ，${\boldsymbol{ \gamma}} = \left( \begin{gathered} 0.01 \\ 0.01 \\ \end{gathered} \right)$ ，则迭代学习律公式为$$ \begin{aligned} {u}_{{k}+1}^{{\rm{ILC}}}(t)=&{\boldsymbol{{u}}}_{{\boldsymbol{k}}}(t)+\left(\begin{array}{l}0.5\\ 0.5\end{array}\right){{\boldsymbol{e}}}_{{\boldsymbol{k}}}(t)+\left(\begin{array}{l}0.05\\ 0.05\end{array}\right){\stackrel{·}{{\boldsymbol{e}}}}_{\boldsymbol{{k}}}(t)+\\ &\left(\begin{array}{l}0.01\\ 0.01\end{array}\right){\displaystyle {\int }_{0}^{t}{{\boldsymbol{e}}}_{{\boldsymbol{k}}}(\tau )}d\tau \end{aligned} $$ (11) （5）为方便比较控制算法的性能优劣，将PID算法与本文提出的PID型ILC算法在收敛速度、跟踪误差等方面进行比较。PID控制算法控制律公式为
$$ {u}_{{\rm{PID}}}(t)={K}_{{p}}{\boldsymbol{e}}({\boldsymbol{t}})+{K}_{i}{\displaystyle {\int }_{0}^{t}{\boldsymbol{e}}({\boldsymbol{\tau}} )}d\tau +{K}_{d}\stackrel{·}{{\boldsymbol{e}}}({\boldsymbol{t}}) $$ (12) 式中，
${K_{{p}}}$ 为比例项增益，${K_{{p}}}$ =5；$ {K_i} $ 为积分项增益，$ {K_i} $ =0.1；$ {K_d} $ 为微分项增益，$ {K_d} $ =10[14]。（6）为量化比较控制算法的跟踪精度，定义跟踪误差率公式为
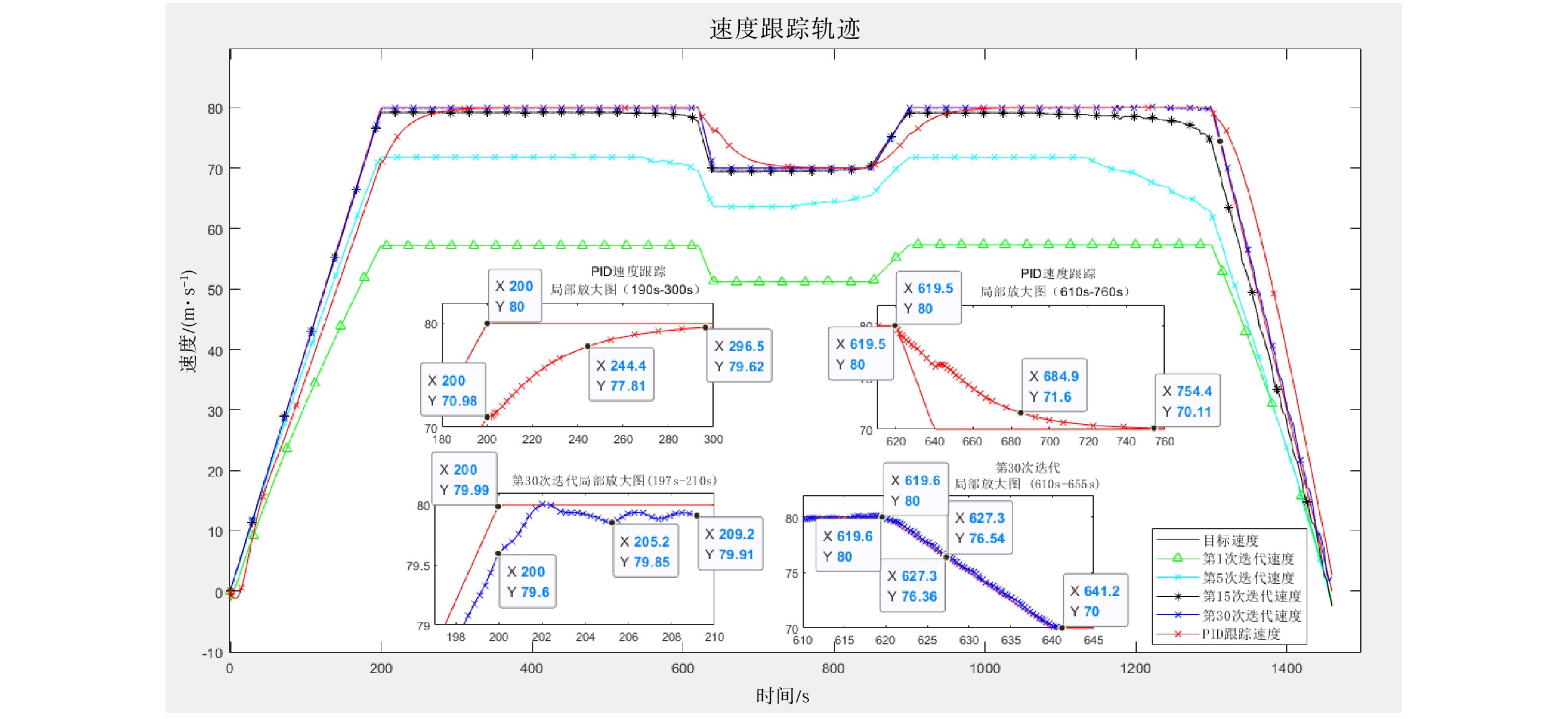
$$ {r_e} = \frac{{\left| {{y_d} - {y_r}} \right|}}{{{y_d}}} \times 100\% $$ (13) 式中，
$ {y_d} $ 为目标值，且$ {y_d} $ >0；${y_r}$ 为实际值；$ {r_e} $ 的取值保留小数点后2位。3.3 仿真结果分析
在公式（11）所示的PID型迭代学习控制器和公式（12）所示PID控制器中运行上述仿真场景，可得到速度跟踪轨迹和位移跟踪轨迹，分别如图2、图3所示。
3.3.1 速度跟踪结果分析
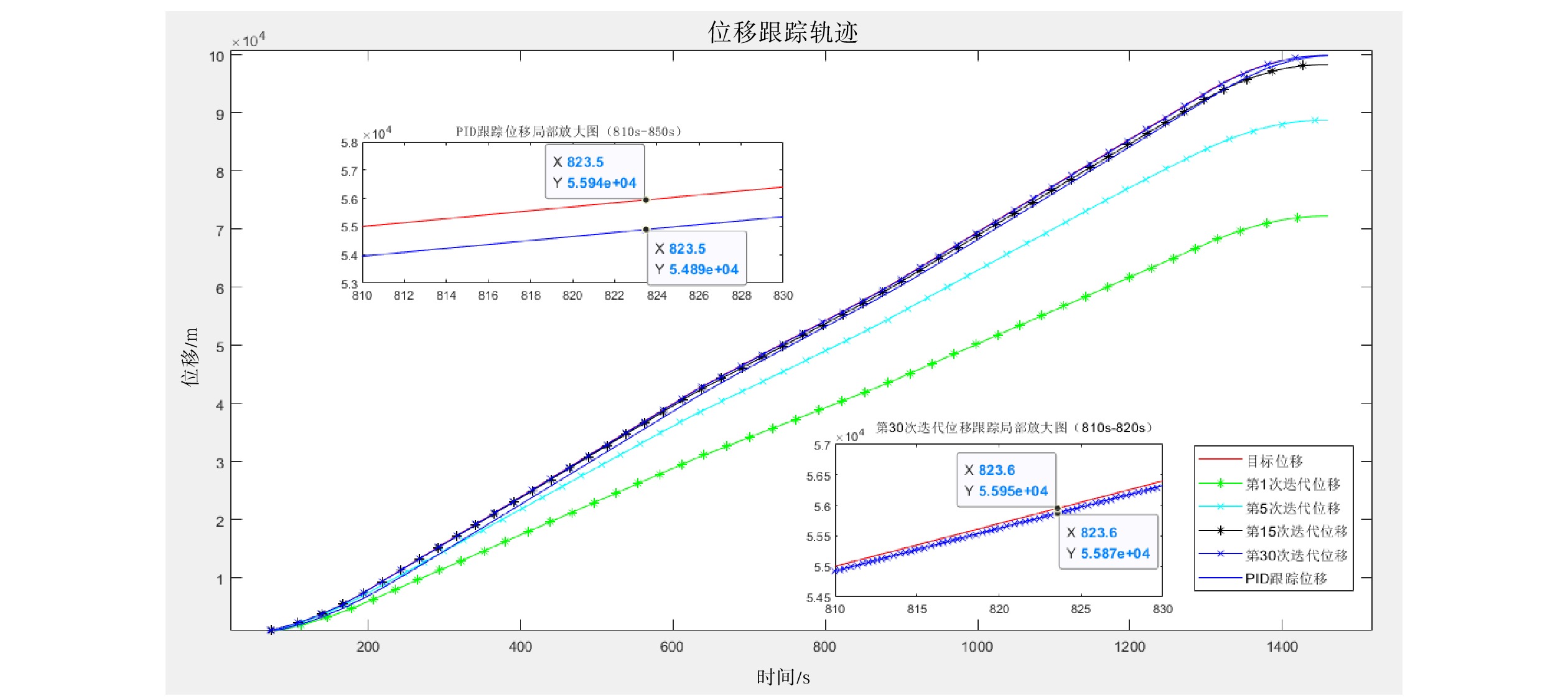
图2给出了PID控制器对目标速度的跟踪轨迹和PID型迭代学习控制器在第1次、第5次、第15次和第30次迭代时对目标速度的跟踪轨迹，以及第30次迭代时在时间区间[197 s，210 s]和[610 s，655 s]上的跟踪轨迹放大图。从图2中选取若干跟踪点，并根据公式（13）得到两种控制器第30次迭代后的速度跟踪误差率
$ {r_e} $ ，如表2所示。表 2 速度跟踪误差率分析时刻/s 目标速度/
（m/s）PID控制器
速度/（m/s）PID控制器
速度$ {r_e} $PID型迭代学习控
制器速度/（m/s）PID型迭代学习
控制器速度$ {r_e} $200 80 70.98 11.28% 79.60 0.50% 205.2 80 79.85 0.19% 209.2 80 79.86 0.18% 244.4 80 77.81 2.74% 296.5 80 79.62 0.48% 619.5 80 80 0% 619.6 80 80 0% 627.3 76.36 76.54 0.24% 641.2 70 70 0% 684.9 70 71.6 2.29% 754.4 70 70.11 0.16% 由表2可知，PID型ILC算法在第30次迭代后的速度跟踪误差均小于1%，明显优于PID算法；此外，对于相同的误差率，PID型ILC算法的实现速率快于PID算法。
3.3.2 位移跟踪结果分析
图3给出了PID控制器对目标位移的跟踪轨迹和PID型迭代学习控制器在第1次、第5次、第15次和第30次迭代时对目标位移的跟踪轨迹，以及第30次迭代时在时间区间 [810 s，835 s]上的位移跟踪轨迹放大图。由图可知，在823.5 s时，目标位移为55940 m，PID控制器的跟踪位移为54890 m，误差为1050 m，
$ {r_e} $ 为1.88%；PID型迭代学习控制器的跟踪位移为55870 m，误差为80 m，$ {r_e} $ 为0.14%。3.3.3 整体分析
从图2、图3可以看出，当迭代开始时，PID型迭代学习控制器的跟踪轨迹与目标轨迹之间存在较大偏差；当迭代次数达到15次以上时，二者基本重合。PID型迭代学习控制器最大跟踪误差绝对值与迭代次数的关系如图4所示。
由图4可知，PID型迭代学习控制器的跟踪误差随着迭代次数的增加逐渐减小，当迭代次数达到25次时，速度和位移跟踪误差接近于0。
综上，PID型ILC算法通过学习列车运行的重复信息，可以快速接近目标速度和位移，实现精确跟踪。
4 结束语
本文分析了高速列车运行动力学模型，根据列车运行过程中的重复性特征，设计了ATO曲线跟踪的ILC算法。将迭代学习控制律加入PID控制律中，通过学习跟踪过程中的误差因素和前次迭代的误差变化率，实现对期望轨迹的精确跟踪。
此外，通过设置典型的仿真环境，利用真实的线路数据和列车参数对所设计算法的性能进行验证，并与现有算法进行对比。仿真结果表明，本文设计的算法具有更高的跟踪精度，随着迭代次数的增加，实际运行轨迹逐渐接近目标轨迹，跟踪误差逐渐减小，且最终收敛于零，从而证明了所提出的算法的有效性和优越性。
-
表 1 高速铁路CRH-3型动车组部分技术参数
参数 取值 编组长度 200.67 m 编组重量 380 t $ {c_a} $ 0.0166 N·h2/(km2·t) $ {c_v} $ 0.228 N·h/(km·t) $ {c_0} $ 7.75 N/t 最高运营速度 350 km/h 平均起动加速度 0.38 m/s2 
下载: 导出CSV
表 2 速度跟踪误差率分析
时刻/s 目标速度/
（m/s）PID控制器
速度/（m/s）PID控制器
速度$ {r_e} $PID型迭代学习控
制器速度/（m/s）PID型迭代学习
控制器速度$ {r_e} $200 80 70.98 11.28% 79.60 0.50% 205.2 80 79.85 0.19% 209.2 80 79.86 0.18% 244.4 80 77.81 2.74% 296.5 80 79.62 0.48% 619.5 80 80 0% 619.6 80 80 0% 627.3 76.36 76.54 0.24% 641.2 70 70 0% 684.9 70 71.6 2.29% 754.4 70 70.11 0.16%
下载: 导出CSV
-
[1] 杨艳飞,崔 科,吕新军. 列车自动驾驶系统的滑模PID组合控制 [J]. 铁道学报,2014,36(6):61-67. [2] 杨宏阔,侯 涛,陈 昱. 基于预测模糊PID控制算法的高速列车优化控制研究 [J]. 铁道运输与经济,2022,44(8):130-136. DOI: 10.16668/j.cnki.issn.1003-1421.2022.08.20 [3] 王龙达,王兴成,刘 罡,等. 城市轨道列车速度曲线预测函数控制改进算法 [J]. 仪器仪表学报,2022,43(2):273-283. DOI: 10.19650/j.cnki.cjsi.J2108765 [4] 唐博伟, 李中奇, 杨 辉. 基于自适应模糊终端滑模控制的高速列车速度跟踪[C]// 第32届中国过程控制会议（CPCC2021）论文集, 2021-07-30, 太原. 北京: 中国自动化学会过程控制专业委员会, 2021: 903. [5] 董 昱,魏万鹏. 基于RBF神经网络PID控制的列车ATO系统优化 [J]. 电子测量与仪器学报,2021,35(1):103-109. DOI: 10.13382/j.jemi.B2003249 [6] 梁新荣,肖 龙,王雪奇,等. 高速列车速度跟踪神经网络PID控制器的设计 [J]. 计算机工程与应用,2021,57(10):252-258. DOI: 10.3778/j.issn.1002-8331.2002-0231 [7] Arimoto S, Kawamura S, Miyazaki F. Bettering operation of Robots by learning [J]. Journal of Robotic Systems, 1984, 1(2): 123-140. DOI: 10.1002/rob.4620010203
[8] 姚文龙,庞 震,池荣虎,等. 基于智能PD型迭代学习控制的清扫车路径跟踪控制 [J]. 青岛科技大学学报(自然科学版),2022,43(1):105-110. DOI: 10.16351/j.1672-6987.2022.01.015 [9] 孟琪迪,南新元,张永兴. 基于PD型迭代学习的机械臂轨迹跟踪控制 [J]. 组合机床与自动化加工技术,2022(11):62-65,69. DOI: 10.13462/j.cnki.mmtamt.2022.11.014 [10] 何之煜,徐 宁. 非参数化迭代学习控制的列车自动驾驶控制算法 [J]. 铁道学报,2020,42(12):90-96. [11] Gao G, Jin S, Wang Q. Model free adaptive iterative learning fault-tolerant control for high-speed trains with speed and input constraints[C]//2021 IEEE 10th Data Driven Control and Learning Systems Conference (DDCLS), 25 June 2021, Suzhou, China. New York: IEEE, 2021: 866-870.
[12] Huang D D, Huang T F, Chen C R, et al. Iterative learning control for high-speed trains with velocity and displacement constraints [J]. International Journal of Robust and Nonlinear Control, 2022, 32(6): 3647-3661. DOI: 10.1002/rnc.5984
[13] Meindl M, Molinari F, Lehmann D, et al. Collective iterative learning control: Exploiting diversity in multi-agent systems for reference tracking tasks [J]. IEEE Transactions on Control Systems Technology, 2022, 30(4): 1390-1402. DOI: 10.1109/TCST.2021.3109646
[14] 何之煜. 自适应迭代学习控制在列车自动驾驶系统中的应用[D]. 北京: 中国铁道科学研究院, 2019. -
期刊类型引用(6)
1. 张吉卫. 地铁实训教学沙盘联锁系统软件设计. 山东交通学院学报. 2023(01): 38-44 . 
百度学术
2. 杨城，杨进. 基于A~*算法的进路搜索应用研究. 铁道通信信号. 2023(05): 20-25 . 百度学术
3. 海玲，刘文，刘智勇，刘岩，王晓辉. 轨道交通自动联锁模拟系统设计. 信息技术. 2023(09): 38-46 . 百度学术
4. 马小娟，王终军，闫福刚，高峰，郭磊，李腾飞. 城轨交通FAO虚拟仿真实训室的设计与实现. 工业控制计算机. 2023(11): 3-5+8 . 百度学术
5. 罗耀云. 铁路车站联锁软件进路搜索算法优化. 电子设计工程. 2021(10): 51-55 . 百度学术
6. 高僮，张亚东，郭进，王建. 列控临时限速场景风险耦合路径自动搜索方法研究. 铁道标准设计. 2021(12): 146-151+167 . 百度学术
其他类型引用(4)
计量
- 文章访问数: 115
- HTML全文浏览量: 21
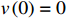
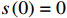
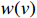
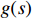
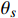
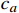
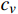
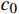
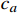
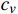
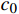
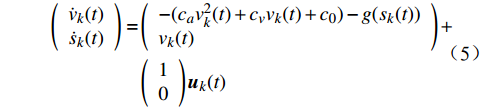
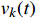
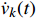
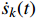
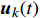
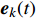
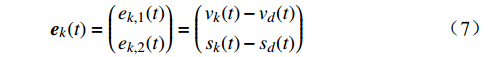
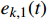
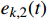
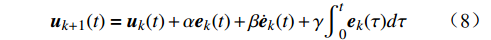
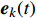
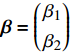
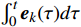
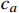
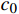
- PDF下载量: 29
- 被引次数: 10
