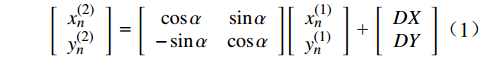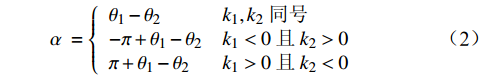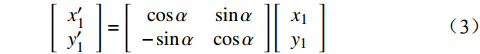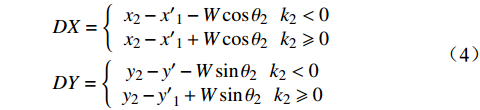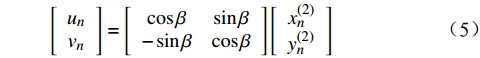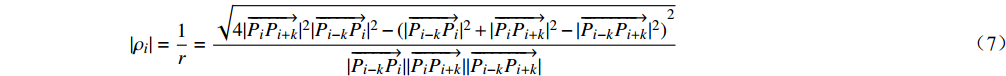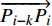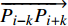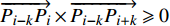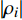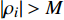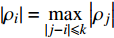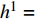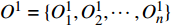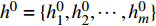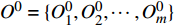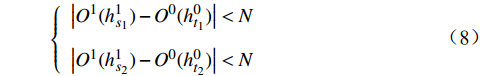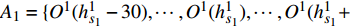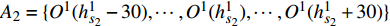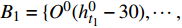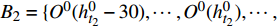随着城市轨道交通（简称：城轨）的快速发展，城轨列车在线运行的安全问题也愈加受到关注。受电弓滑板是城轨列车的重要电气部件，用于收集接触线上的电流，为城轨列车提供动力。在城轨列车运行过程中，受电弓滑板与接触线直接接触，二者间的相互作用导致受电弓滑板的持续磨耗，其磨耗状态对城轨列车的安全运营有着较大影响。因此，对受电弓滑板磨耗状态进行及时监测是保障城轨列车运营安全的一项重要措施^[1]。

人工检测法因其操作便捷、灵活性强的特点，仍是当前受电弓滑板磨耗检测的主要方法，但该方法需要人工登顶对受电弓滑板磨耗进行检测，检测效率低、安全性差，且检测结果受人为因素影响较大^[2]。随着信息技术的飞速发展，城轨车辆关键部件的自动化智能检测已成为趋势。近年来，自动化检测设备在弓网领域取得了较大进展，计算机视觉及激光等技术被用于弓网系统的故障诊断和状态监测。Karakose等人^[3]提出一种基于图像处理的受电弓故障诊断方法，对受电弓滑板与接触线的接触点进行监测，并根据接触点数量将受电弓滑板分为安全、危险、故障3个区域，但该方法未对滑板磨耗的具体数值进行计算；朱晓恒等人^[4]和黄艳红等人^[5]使用边缘检测算法检测受电弓滑板的剩余磨耗，但所用方法对磨耗检测的准确性有待改进；魏秀琨等人^[6]提出一种基于图像处理技术和深度学习的智能检测方法，用于受电弓滑板的在线监测，采用神经网络模型来检测受电弓滑板的故障类别，再基于亚像素等图像处理技术对受电弓滑板的磨耗进行定量分析，但该方法的检测精度仍有待提高；路绳方等人^[7]提出一种基于多视图分析的滑板磨耗测量系统，采用亚像素边缘检测和3D重构技术实现滑板磨耗量的检测，但滑板磨耗曲线的重构精度受滑板复杂的背景环境影响较大。上述研究都是基于图像处理对受电弓滑板的状态进行分析，但受电弓弓头附近照明亮度和复杂的背景环境会增加算法处理的难度，不可避免地影响受电弓滑板检测的准确性和稳定性。

随着激光位移传感器（简称：激光传感器）技术的快速发展，激光传感器在铁路领域内得到了广泛的应用。滕云等人^[8]设计一种基于二维激光传感器的钢轨波纹精确测量系统，通过二维传感器对钢轨数据进行采样，再采用数据拼接方法完成对钢轨波纹的精确还原；程晓卿等人^[9]将激光位感器运用到列车轮对尺寸的检测中，通过多组激光传感器的配合，实现列车车轮轮缘尺寸和轮径的测量。但采用激光传感器对受电弓滑板的状态进行分析的研究尚少。

本文提出一种基于激光传感器的城轨列车受电弓滑板磨耗检测方法。采用2组激光传感器采集受电弓滑板上表面轮廓线，通过数据筛选、数据融合、滑板校正等方法获取受电弓滑板的实际轮廓线，再将滑板实际轮廓线与标准轮廓线进行曲线配准，获得滑板的磨耗曲线，从而实现受电弓滑板磨耗的非接触式在线检测。

1   硬件设计

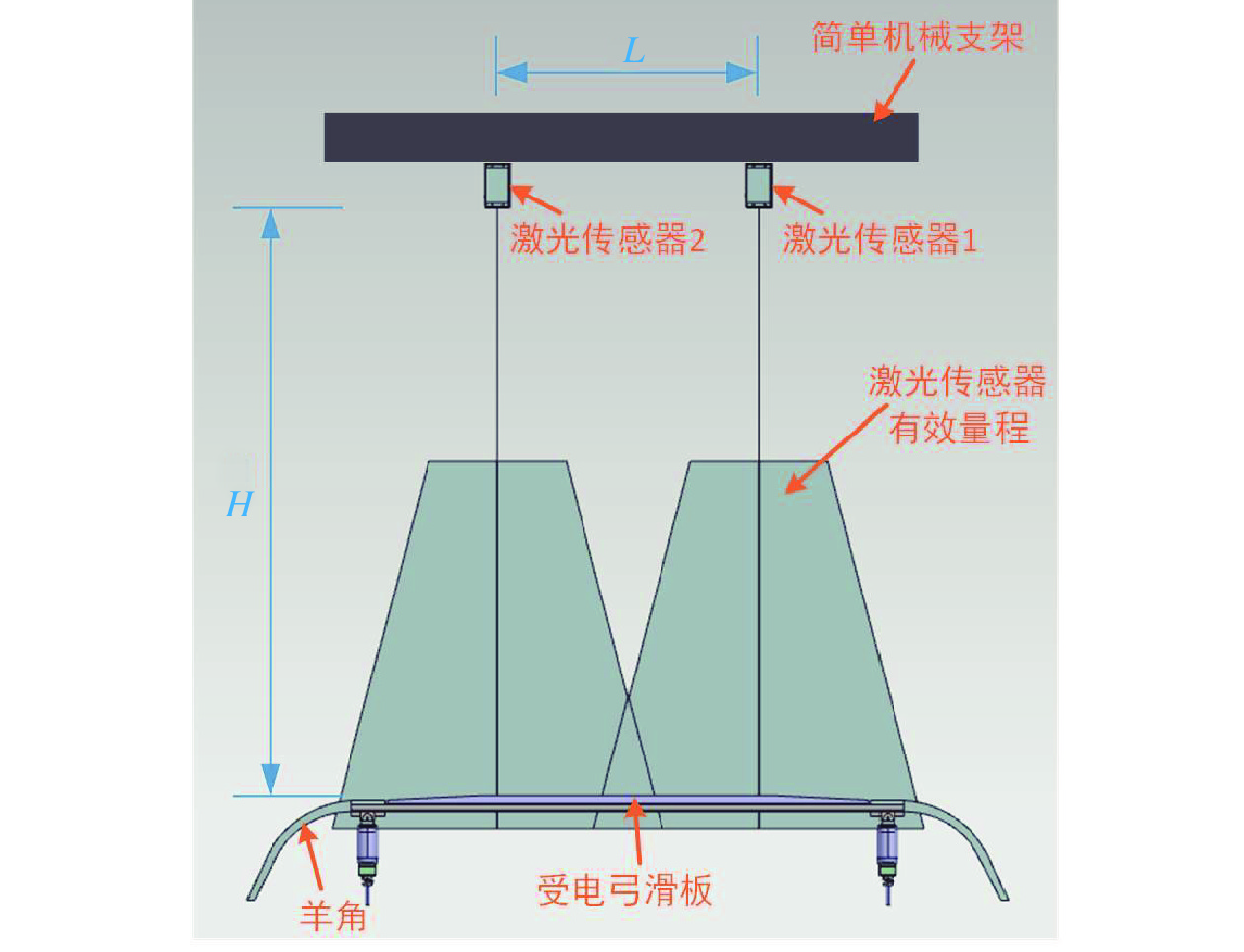
由于激光测量具有速度快、精度高的特点，本文基于激光传感器设计了受电弓滑板磨耗检测装置（简称：检测装置）。检测装置由2组激光传感器组成，安装于受电弓滑板上方，垂直向下安装，对受电弓滑板表面轮廓数据进行采集。2组激光传感器的相对空间位置关系对受电弓滑板磨耗的检测结果至关重要，检测装置的设计标准为：（1）2组激光传感器的激光平面位于同一平面上；（2）2组激光传感器自身坐标系的 x 轴要相互平行， y 轴也要相互平行；（3）受电弓滑板位于激光传感器的有效量程范围内，在滑板水平方向上，2组激光传感器协同配合完成完整受电弓滑板数据的采集，且2条激光线存在交叠区，便于后期的数据融合处理；（4）2组激光传感器关于轨道中心线镜面对称。

受电弓滑板磨耗检测装置组成如图1所示，2组激光传感器固定安装在同一机械支架上，激光垂直往下照射，激光源点距滑板上表面的垂直距离为 H，2个激光源点之间的水平距离为 L。结合滑板长度及激光传感器的有效量程，可对参数 H 和 L 进行设计，本文设计值为 L=680 mm、H=1330 mm。图中，梯形区域代表激光传感器的有效量程，在滑板水平方向，2组激光传感器发射的激光线能够覆盖完整的受电弓滑板且存在交叠区。

图  1  受电弓滑板磨耗检测装置组成

下载: 全尺寸图片 幻灯片

2   受电弓滑板磨耗检测算法

本文设计的受电弓滑板磨耗检测算法主要包括数据筛选、数据融合、倾斜校正、曲线配准和磨耗计算等5个步骤。

2.1   数据筛选

城轨列车通过检测装置时，激光传感器进行连续采样，当受电弓滑板在激光传感器有效量程范围外时，激光传感器无有效数据输出；当其在测量范围内时，激光传感器输出有效数据。受电弓滑板进入与离开检测区域时，激光传感器输出点数有明显的上升和下降现象，因此，可通过判断激光传感器输出数据点数是否大于固定阈值，来进行受电弓滑板有效数据段的筛选。

2.2   数据融合

筛选出有效数据段后，需要将2组传感器在同一时刻采集的数据进行数据融合，得到受电弓滑板的完整轮廓，但受现场安装条件和支架加工精度的影响，2组激光传感器实际安装的位置和角度都不是理想的设计值，无法简单根据设计参数进行数据拼接。为保证2组激光传感器融合后的曲线能够符合滑板曲线实际情况，需要对激光传感器坐标系进行旋转变换和平移操作，将2组激光传感器采集的数据转换到同一个坐标系中。

2.2.1   坐标系转换

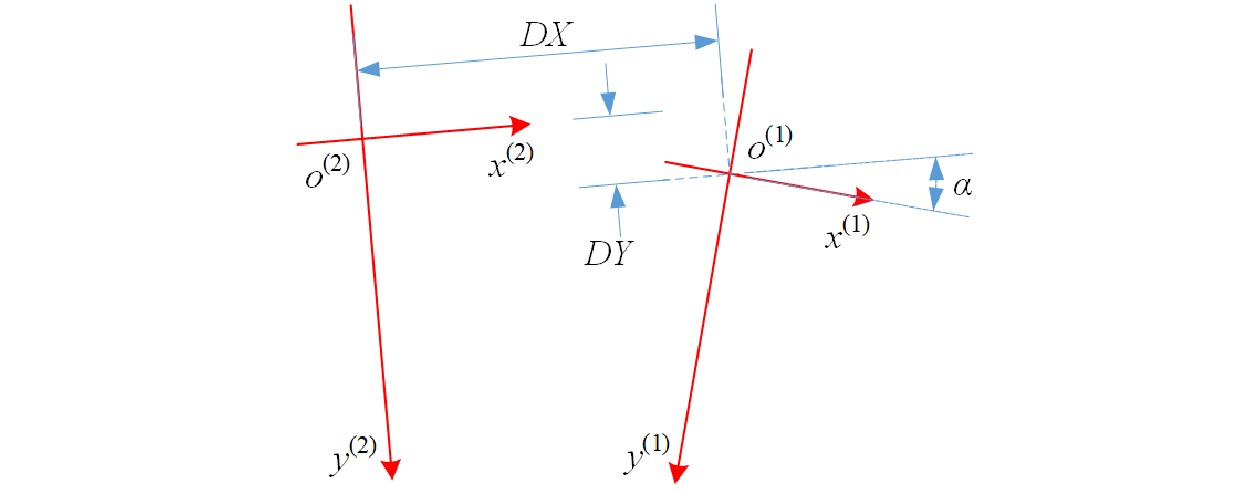
激光传感器数据融合坐标系转换示意如图2所示。激光传感器坐标系以激光源为原点，激光发射面的角平分线为 y 轴，x 轴在二维激光平面内垂直于y 轴，激光传感器1、2的坐标系分别为 x⁽¹⁾ o⁽¹⁾ y⁽¹⁾和x⁽²⁾ o⁽²⁾ y⁽²⁾。本文以激光传感器2的坐标系为目标坐标系，将激光传感器1的坐标系旋转平移到激光传感器2的坐标系，具体转换公式为

图  2  激光传感器数据融合坐标系转换示意

下载: 全尺寸图片 幻灯片

式中，( x_n⁽¹⁾ , y_n⁽¹⁾ )、( x_n⁽²⁾ , y_n⁽²⁾ )分别为坐标系 x⁽¹⁾ o⁽¹⁾ y⁽¹⁾、x⁽²⁾ o⁽²⁾ y⁽²⁾ 上的点，α 为 x⁽¹⁾ 轴和 x⁽²⁾ 轴间的夹角，DX、DY 分别为2个坐标系原点的空间距离。

2.2.2   参数求解

数据融合的关键在于参数α、DX 和 DY 的求解，本文采用基于标定块的融合参数计算方法，借助精加工的标定块，实现对这3个参数的计算。假设标定块宽度为 W，标定过程中2个激光传感器需要照射在同一条直线上，将多次标定的均值作为最终的标定结果。

（1）旋转角α求解

根据2条激光线照射在标定块上同一条直线的特征，实现坐标系旋转角的计算。对2组激光传感器采集到的数据进行线性拟合，拟合的直线分别为l₁、l₂，直线斜率分别为k₁、k₂，倾斜角分别为θ₁、θ₂，则旋转角α计算公式为

（2）平移参数 DX、DY 的求解

将2组激光传感器的激光照射在标定块的同一条直线上，激光传感器1和2各检测到标定块的1个边界点，边界点在各自激光传感器坐标系的坐标分别为( x₁, y₁ )、( x₂, y₂ )。传感器1的坐标系旋转角为α，则点( x₁, y₁ )旋转后的坐标为$({x'_1},{y'_1})$，转换公式为

激光传感器1的坐标系旋转后，其坐标轴与传感器2的坐标轴相互平行，但坐标原点存在一定的空间位置差。根据标定块固定长度的特征，对坐标原点在 x 轴方向上的平移距离 DX 和 y 轴方向上的平移距离 DY 进行计算，公式为

2.3   倾斜校正

受传感器安装角度、受电弓运行姿态等因素的影响，激光线并不能垂直照射在受电弓滑板的上表面，因此，需要对融合的数据进行倾斜校正，以保证受电弓滑板磨耗曲线的准确性，融合数据的校正公式为

式中，( x_n⁽²⁾ , y_n⁽²⁾ )为融合后的数据点；( u_n , v_n )为校正后的数据点；β为倾斜校正角。

由公式（5）可知，校正的关键在于校正角β的求解，校正角求解过程主要分为数据分段和倾斜角计算2部分。

2.3.1   数据分段

受电弓滑板的装配结构（局部）如图3所示。根据受电弓滑板装配结构特征，将融合后的数据分为5段，依次为左羊角数据、左空隙数据、滑板数据、右空隙数据和右羊角数据。激光传感器垂直向下安装，空隙数据在 y 轴方向上的值相比于其他位置数据具有一定幅值的突变，基于这一特征，本文采用连续边缘提取（SEF，Successive Edge Following）算法，对数据点进行分段。从起点( x₁⁽²⁾ , y₁⁽²⁾ )开始，按照顺序进行搜索，计算相邻两点{( x_n⁽²⁾ , y_n⁽²⁾ ) , ( x_n+1⁽²⁾ , y_n+1⁽²⁾ )}的欧式距离 d，与阈值 Δd 进行比较，若 d < Δd，则把后续点( x_n+1⁽²⁾ , y_n+1⁽²⁾ )加入到同一点集 R_c={( x₁⁽²⁾ , y₁⁽²⁾ ) ,···, ( x_n⁽²⁾ , y_n⁽²⁾ ) , ( x_n+1⁽²⁾ , y_n+1⁽²⁾ )}中；若 d ≥ Δd，则以点( x_n⁽²⁾ , y_n⁽²⁾ )为分割点，下一个点集 R_c+1 以( x_n+1⁽²⁾ , y_n+1⁽²⁾ )为起点继续搜索。数据分段完成后，统计各个点集的数据点数量 N_c，并与阈值 Δn 进行比较，若 N_c ≤ Δn，则将该数据点集滤除，该点集内的数据点被认为是无效数据。

图  3  受电弓滑板装配结构（局部）

下载: 全尺寸图片 幻灯片

2.3.2   倾斜角计算

数据分段完成后，通过阈值Δn的设置，可将非滑板数据点集滤除，只保留滑板数据点集。根据滑板的结构特征和磨耗位置，将滑板数据分为左斜边、水平和右斜边3个区域，如图4所示。除去水平区域，其余2个区域在正常情况下都不会与接触网接触并发生磨耗，本文基于左、右斜坡区域的角度特征实现受电弓滑板倾斜角的计算，公式为

图  4  滑板磨耗区域划分

下载: 全尺寸图片 幻灯片

式中，δ₁、δ₂分别是左斜坡区域、右斜坡区域的数据点进行一阶线性拟合后，在受电弓滑板水平方向上的倾斜角。

2.4   曲线配准

本文采用迭代局部特征段（ILFS ，Iterative Local Feature Segment）算法进行受电弓滑板实际磨耗轮廓与标准轮廓匹配的配准工作，具体过程如下。

2.4.1   轮廓特征点检测

曲线配准的前提是对受电弓滑板实际磨耗轮廓和标准轮廓进行特征点检测工作，本文以滑板实际磨耗轮廓为例进行特征点检测说明。选取受电弓滑板实际轮廓线上的任意一点 P_i ( x_i , y_i )，其前后两点为 P_i-k ( x_i-k , y_i-k )，P_i+k ( x_i+k , y_i+k )，将 P_i 、P_i-k 、P_i+k 这3个点进行圆弧拟合，记拟合后的圆弧所在圆的半径为 r，P_i 点的曲率为 ρ_i，Ω ( P_i ) ={P_i-k, ···, P_i-1, P_i, P_i+1, ···, P_i+k} 为点 P_i ( x_i , y_i ) 的覆盖区域，在覆盖区域内，P_i 处的曲率公式为

计算受电弓滑板实际磨耗轮廓上各点的曲率，考虑向量$ \overrightarrow {{P_{i - k}}{P_i}} $ 和$ \overrightarrow {{P_{i - k}}{P_{i + k}}} $ 的矢量积，当$ \overrightarrow {{P_{i - k}}{P_i}} \times \overrightarrow {{P_{i - k}}{P_{i + k}}} \geqslant 0 $时，曲线在P_i处是凸的，反之则是凹的。计算实际磨耗轮廓线上每个点曲率的绝对值 ${\text{|}}{\rho _i}{\text{|}}$，设定阈值M，当 ${\text{|}}{\rho _i}{{| > M}}$ 时，将 P_i 标记为候选特征点，通过非极大抑制对候选特征点进行筛选，即当 $ \left| {{\rho _i}} \right| = \mathop {\max }\limits_{|j - i| \leqslant k} \left| {{\rho _j}} \right| $ 时，P_i 成为特征点。

2.4.2   搜索初始匹配点

计算受电弓滑板实际磨耗轮廓和标准轮廓各点的曲率，根据上述特征点判定规则，分别得到2条轮廓的特征点集。假定受电弓滑板实际磨耗轮廓特征点集记为$ {h^1} = \{ h_1^1,h_2^1, \cdots ,h_n^1\} $，相对应曲率记为${O^1} = \{ O_1^1,O_2^1, \cdots ,O_n^1\} $，标准轮廓特征点集记为$ {h^0} = \{ h_1^0,h_2^0, \cdots ,h_m^0\} $，相对应的曲率记为${O^0} = \{ O_1^0,O_2^0, \cdots ,O_m^0\} $，n、m 分别为受电弓滑板实际轮廓和标准轮廓上的特征点个数。搜索受电弓滑板实际磨耗轮廓和标准轮廓的特征点，如果满足公式（8），则受电弓滑板实际轮廓的第s₁、s₂个特征点和标准轮廓的第t₁、t₂个特征点初始匹配。

式中，N为误差度量。

2.4.3   确定候选匹配点

分别计算候选匹配曲线段2个特征点间的弦长 L₁、L₂。如果满足 L₁−L₂ < ε，ε 为最大允许误差，则2个弦长在误差允许的范围内，判定两段曲线匹配；否则，返回2.4.2中的步骤，重新搜索。

2.4.4   确定匹配数据段

由于标准轮廓曲线是未磨耗的受电弓滑板轮廓线，而目标轮廓曲线为磨耗后的受电弓滑板轮廓线，二者不可能完整匹配，已知受电弓滑板受到的磨耗只有水平区域，两端的斜坡区域是不被磨耗的，因此，对两端不被磨耗的部分进行匹配即可完成轮廓线的配准。

选择滑板实际磨耗轮廓的第s₁、s₂个特征点的左右各30个点作为未磨耗部分轮廓，相对应的数据点集分别记为$ {A_1} = \{ {O^1}(h_{{s_1}}^1 - 30), \cdots ,{O^1}(h_{{s_1}}^1), \cdots , {O^1}(h_{{s_1}}^1 + 30)\} $、$ {A_2} = \{ {O^1}(h_{{s_2}}^1 - 30), \cdots ,{O^1}(h_{{s_2}}^1), \cdots , {O^1}(h_{{s_2}}^1 + 30)\} $。同理，选择标准轮廓的第t₁、t₂个特征点的左右各30个点，相对应的数据点集分别记为$ {B_1} = \{ {O^0}(h_{{t_1}}^0 - 30), \cdots , {O^0}(h_{{t_1}}^0), \cdots ,{O^0}(h_{{t_1}}^0 + 30)\} $、$ {B_2} = \{ {O^0}(h_{{t_2}}^0 - 30), \cdots ,{O^0}(h_{{t_2}}^0), \cdots , {O^0}(h_{{t_2}}^0 + 30)\} $。对滑板两侧不被磨耗的部分进行匹配即可完成轮廓线的配准，即进行s₁特征点段曲线和t₁特征点段曲线匹配，s₂特征点段曲线和t₂特征点段曲线匹配。计算 A₁、B₁和 A₂、B₂ 之间的Hausdorff距离为 D ( A ₁ , B ₁ ) 和 D ( A ₂ , B ₂ )^[10]，如果 D ( A₁ , B₁ ) 和 D ( A₂ , B₂ )小于设置的误差阈值，则表示轮廓匹配成功；否则，重新搜索匹配数据段。

2.5   滑板磨耗计算

曲线配准完成后，需将实际轮廓与标准轮廓做减操作，以获取受电弓滑板的磨耗值。但两者数据点的间距不同，无法直接进行减操作。本文以实际磨耗轮廓的数据点横向坐标为基准，对标准轮廓进行局部多项式曲线拟合，再进行减操作，获得受电弓滑板的实际磨耗值。

3   试验与分析

3.1   磨耗试验过程

为验证本文设计的基于激光传感器的受电弓滑板磨耗检测方法，搭建的受电弓滑板磨耗检测装置如图5所示，2组激光传感器固定安装在同一机械支架上，激光垂直向下照射受电弓滑板的上表面。

图  5  受电弓滑板磨耗检测装置

下载: 全尺寸图片 幻灯片

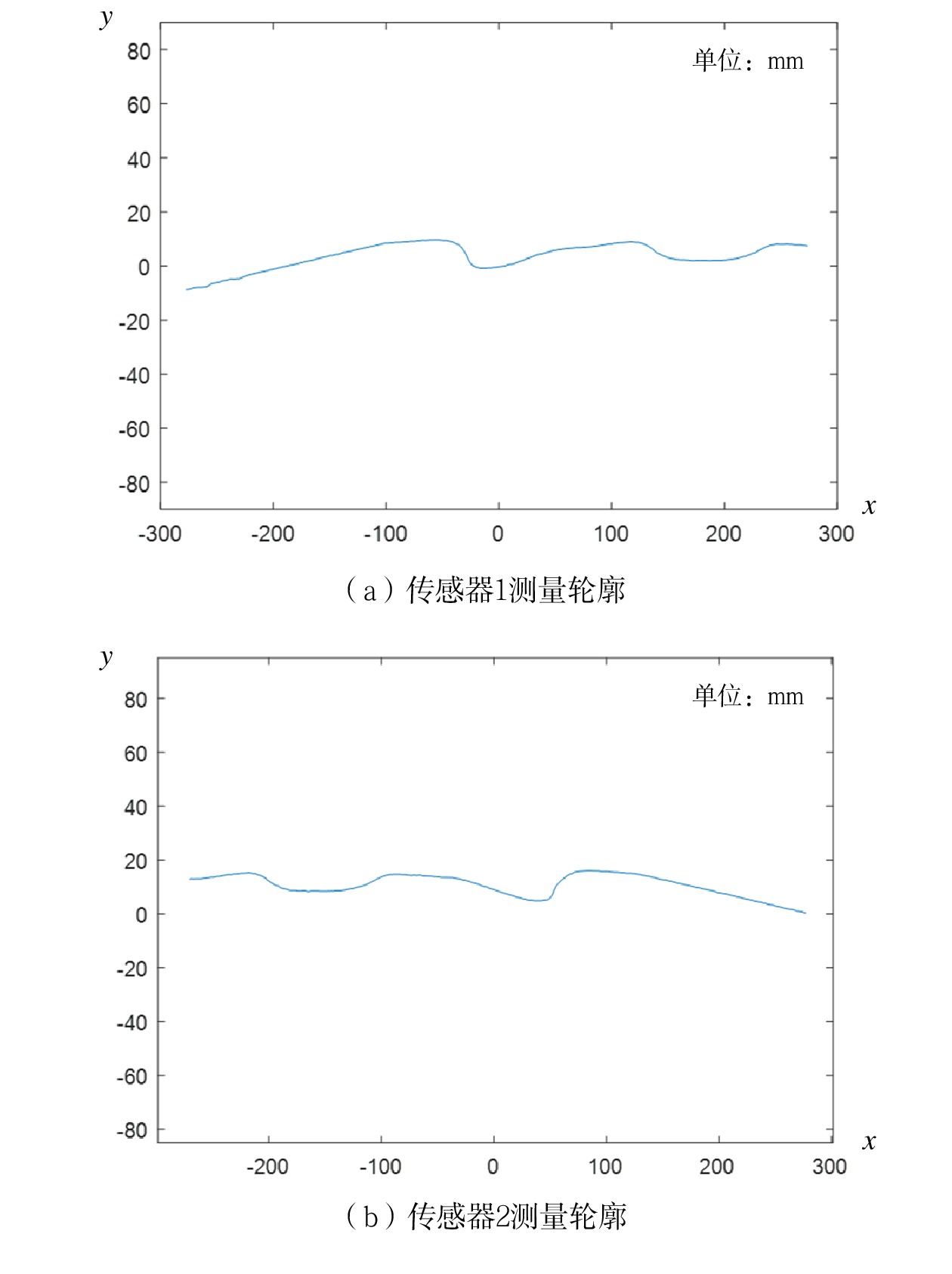
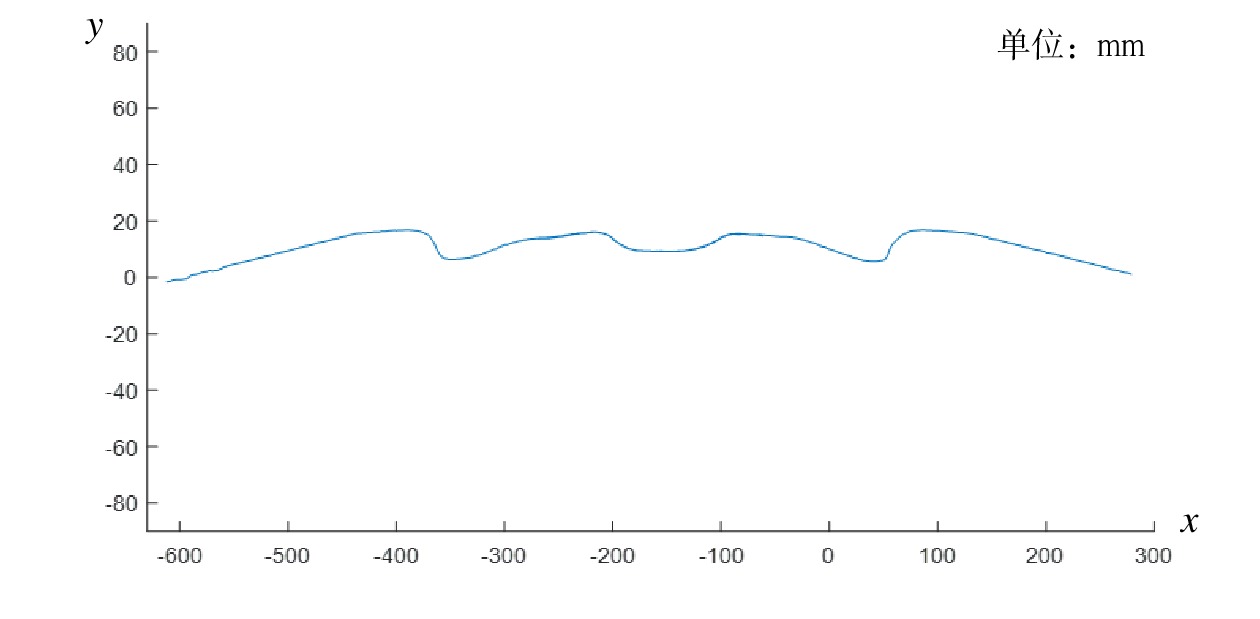
2组激光传感器检测得到的受电弓滑板轮廓数据如图6所示，经数据融合、倾斜校正后得到的完整受电弓滑板轮廓曲线，如图7所示。图6、图7中横纵坐标表示受电弓滑板轮廓数据在自建坐标系中的位置信息。

图  6  传感器测量滑板轮廓

下载: 全尺寸图片 幻灯片

图  7  完整的受电弓滑板轮廓

下载: 全尺寸图片 幻灯片

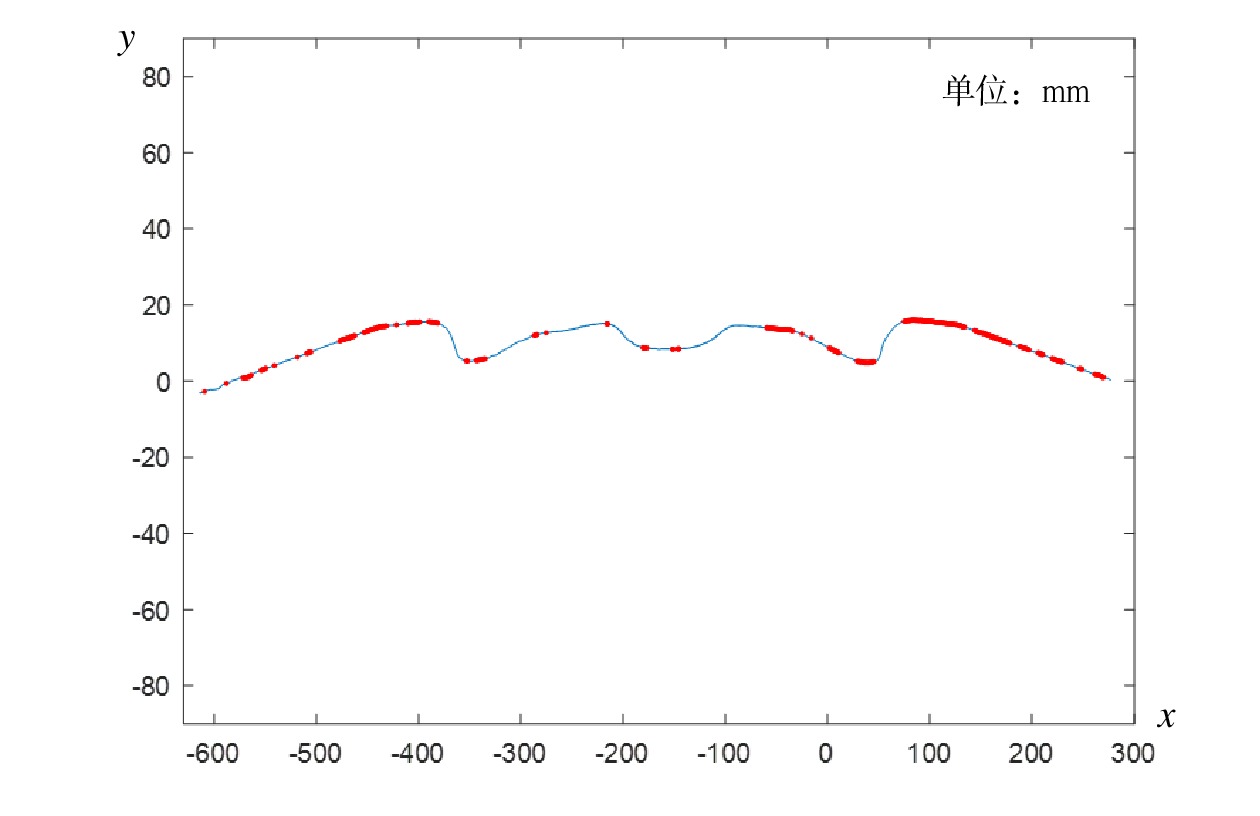
将受电弓滑板实际轮廓与标准轮廓进行曲线配准，特征点检测结果如图8所示。选取受电弓滑板左右未磨耗区域的特征点进行曲线匹配，匹配结果如图9（a）所示，图中蓝色曲线为标准轮廓，红色曲线为受电弓滑板实际磨耗轮廓。图8、图9中横纵坐标表示受电弓滑板轮廓数据在自建坐标系中的位置信息。

图  8  特征点检测

下载: 全尺寸图片 幻灯片

图  9  不同算法曲线配准结果

下载: 全尺寸图片 幻灯片

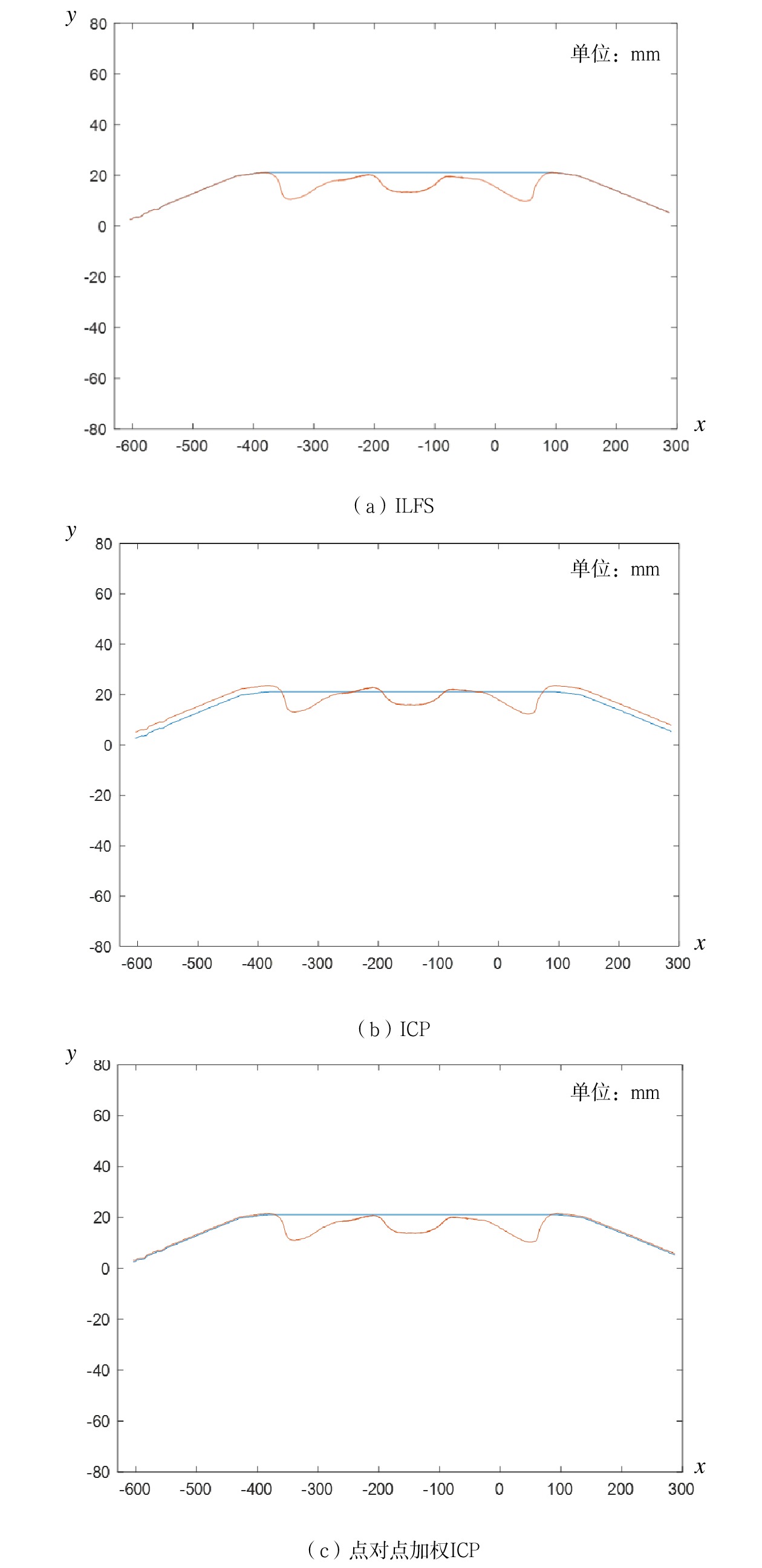
ILFS算法的曲线配准结果如图9（a）所示。为验证本文所用ILFS算法的曲线配准性能，选择最近点迭代（ICP ，Iterative Closest Point）算法^[11]和点对加权ICP算法^[12]进行对比，2者的曲线匹配结果如图9（b）、图9（c）所示。由图9可知，ILFS算法和点对加权ICP算法的配准结果比较准确，而传统ICP算法配准结果不佳。

由于ICP算法配准效果较差，本文仅将ILFS算法和点对加权ICP算法的配准效果进行进一步对比。以2条轮廓线匹配点对间的欧式距离的平均值作为曲线配准的精度，ILFS算法的配准精度为0.22 mm，点对加权ICP算法的配准精度为1.85 mm，ILFS算法具有显著优势。

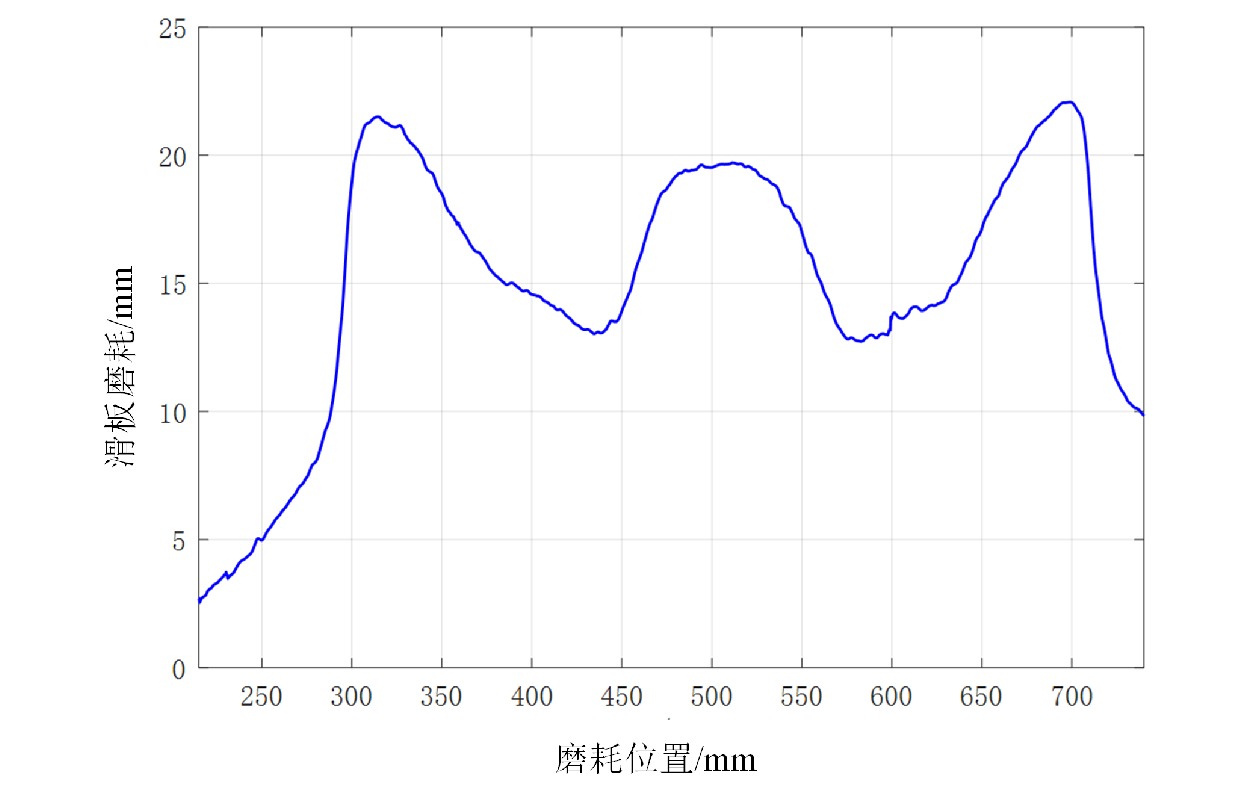
曲线配准完成后，将标准轮廓与实际轮廓做减操作，获得受电弓滑板的磨耗曲线，如图10所示，横坐标表示滑板的磨耗位置。

图  10  受电弓滑板磨耗曲线

下载: 全尺寸图片 幻灯片

3.2   检测结果的验证与分析

由图10可知，受电弓滑板最大磨耗值为22.07 mm，该滑板人工测量最大磨耗值为22.4 mm，误差为0.33 mm。为进一步验证激光检测方案的精度，选取10组滑板进行测量，检测结果如表1所示。

表  1  滑板磨耗测量结果

编号	人工检测/mm	本文方法/mm	误差/mm
1	10.7	11.15	0.45
2	3.0	2.66	0.34
3	3.3	3.56	0.26
4	9.1	8.64	0.16
5	7.3	6.91	0.39
6	11.1	11.35	0.25
7	12.0	12.26	0.26
8	9.4	9.05	0.35
9	8.3	8.51	0.21
10	10.4	10.87	0.47

下载: 导出CSV 

| 显示表格

由表1可知，10根滑板的磨耗误差均在0.5 mm以内，平均检测误差为0.34 mm。文献[13]提出的基于图像处理的受电弓滑板磨耗检测系统，实现了0.8 mm的滑板磨耗检测精度。因此，本文提出的基于激光传感器的受电弓滑板磨耗检测方法，相较于文献[13]一类传统的基于图像处理的磨耗检测方法，剔除了大量无用背景信息的干扰，提升了滑板磨耗检测精度，误差控制在0.5 mm以内，能够满足受电弓滑板检测的需求。

4   结束语

本文提出了一种基于激光传感器的受电弓滑板磨耗检测方法，给出了基于激光传感器的受电弓滑板磨耗硬件设计方案，阐明了检测算法中数据筛选、数据融合、倾斜校正、曲线配准和磨耗计算等5个步骤的具体过程，并通过试验验证了所提方法的可靠性。试验结果表明，本文提出的受电弓滑板磨耗检测方法具有较高的检测精度，能够满足受电弓滑板磨耗检测的精度需求。