Web lightweight strategy and loading optimization method for subway BIM model
-
摘要: 地铁BIM（Building Information Modeling）模型具有体量大、构件重复率高、外形规整等特点，针对其Web端模型加载、渲染效率低下，易导致浏览器卡顿、页面崩溃等问题，提出地铁BIM模型Web端轻量化策略及加载优化方法。验证表明，采用恰当的模型轻量化手段可显著减少复杂建筑模型的面片数量，降低模型存储消耗，结合视锥体剔除算法，能够有效提高渲染帧率与用户交互流畅度。Abstract: The Building Information Modeling (BIM) model for subway buildings has the characteristics of large volume, high component repetition rate, and regular appearance. Aiming at the low efficiency of its Web side model loading and rendering, which could easily lead to browser jams, page crashes, and other issues, this paper proposed a subway BIM model Web side lightweight strategy and load optimization method. Experiments show that using appropriate model lightweight methods can greatly reduce the number of patches in complex architectural models, reduce model storage consumption, and combine visual cone culling algorithms to effectively improve rendering frame rate and user interaction fluency.
-
BIM（Building Information Modeling）技术是运用计算机对建筑的物理特征与功能特性进行数字化建模、管理和可视化表达的一项技术。BIM技术能够在工程项目的规划、勘察、设计、施工、运营维护等各阶段实现模型的集中存储、统一管理、数据交换与共享，并支持各专业的设计决策和协同工作，对建筑业提质增效、精细化管理具有重要的意义[1-2]。然而在实际运用过程中，鉴于BIM模型体量大、构件多、结构精细，其Web端的模型加载、渲染效率低下，严重影响用户的交互体验，极大地限制和阻碍了应用落地。如何实现模型的高效压缩、存储、传输、加载和渲染，解决大体量复杂BIM模型的可视化已成为Web端BIM信息化平台研发的关键[3-4]。
本文针对BIM模型特点，探讨了若干Web端模型渲染轻量化策略，包括网格压缩、减面、模型多细节层次（LOD，Levels of Detail）及模型缓存，同时提出了基于视锥体的快速渲染方法。开发实践表明，本文提出的方案能较好解决大规模复杂模型的交互和浏览问题。
1 地铁BIM模型特点及分类
目前三维模型轻量化已有很多成熟的技术，然而在实际项目中，不同领域的模型具有不同的特点，因此针对不同情况需要选择恰当的模型轻量化策略，确保在提升模型渲染效率的同时，模型不失真、无破损。本文以广州地铁某站点BIM模型为研究对象，全面分析各专业模型的特点，探讨其模型轻量化对策。
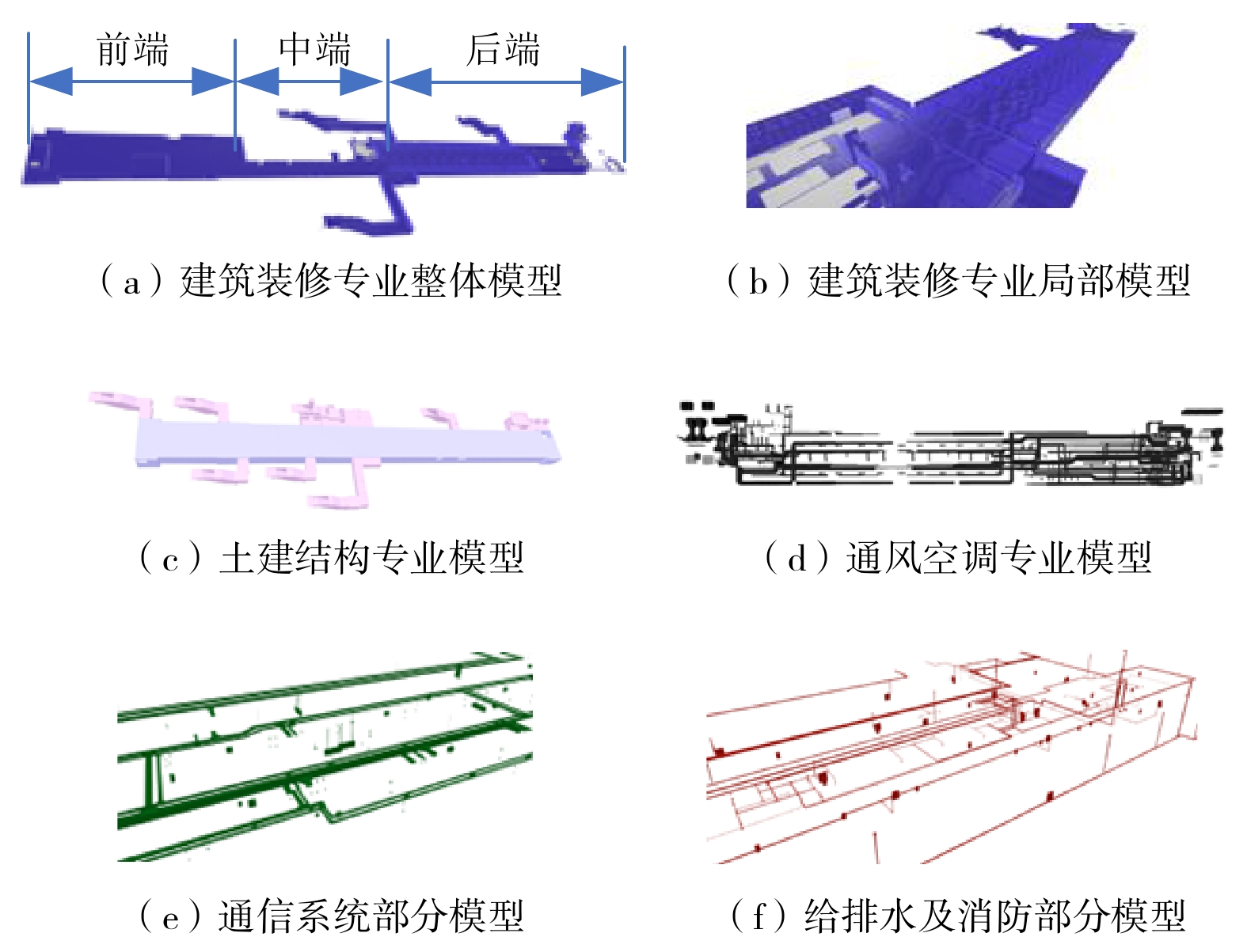
地铁建设涉及建筑、结构等30余个一级专业，以及桥梁、路基等80余个二级专业。本文对模型特点进行归纳总结，选出5个典型复杂专业进行研究，如图1所示。
所选站点建筑装修专业模型体量大、构件多、结构复杂，该专业模型包含5个楼层、5.7万余个构件、400余万个三角面片；土建结构、通风空调专业的模型由板、梁、风管、箱体等构成，其外形表现为比较规则的几何形体；通信、给排水及消防专业的模型由大量的管、线，以及分散部件（摄像机、消防栓）构成，模型相对稀疏。各专业模型体量差异较大，如表1所示，建筑装修专业模型的构件（楼板、墙砖、踢脚线）重复率最大，是Web3D模型轻量化的重点和难点。
表 1 地铁线路不同专业BIM模型体量对比专业 模型大小/M 构件数量 顶点数量 面片数量 RVT IFC GLB 建筑装修 519 301 127 57 360 12 390 176 4 130 058 通风空调 51.2 122 54.1 10 125 2 657 562 885 854 给排水及消防 53.4 43.4 25.1 3 042 686 781 468 495 土建结构 63.6 16.4 6.5 1 164 164 528 117 964 通信系统 30.3 6.9 1.4 784 33 030 24 245 2 地铁BIM模型轻量化策略
在Web3D中，浏览器加载的模型文件以字符串形式存储在JavaScript变量中。而谷歌浏览器可加载的最大模型为512 M，限制了场景内模型的整体规模。模型渲染优化分为离线模型轻量化（包括减面、减顶点来降低模型体量）和加载优化2个方面，本节提出若干加载前模型轻量化策略。为了实现大场景、多专业、复杂模型的Web渲染，针对不同专业的模型，可以采取如下轻量化处理策略。
2.1 数模分离提取模型几何信息
由表1可知，由于RVT、IFC格式的模型文件包含大量的属性信息，因此模型体量相对较大。目前，基于Web的系统架构已成为BIM信息化平台开发的主流[5-6] ，作为浏览器端一种高效、可扩展、跨平台的三维模型表达，GLB/GLTF格式可以最大限度地精简模型，此外，由于其提供了完整的场景表达（包括场景、摄像机、动画、网格、材质、纹理、渲染技术、着色器以及着色器程序等），目前已成为事实上的Web3D对象标准。因此，BIM模型轻量化的第一步就是实现模型属性与几何数据的分离。
从RVT/IFC格式的模型中提取属性信息存储在数据库中，将分离出的模型几何数据转储为GLB/GLTF格式的模型文件。数模分离后，浏览器加载模型时，只需要关注模型的几何信息，从而有效减小浏览器端模型加载的时间，提高渲染效率。
2.2 模型抽取与LOD技术
LOD技术指根据物体模型的节点在显示环境中所处的位置和重要度，决定物体渲染的资源分配，降低非重要物体的面数和细节度，从而获得高效率的渲染运算。建筑装修、土建结构专业的模型一般具有较为丰富的层次结构，由外到内由多层构件组成。针对这类模型，可采用光线扫描法逐层抽取模型构件，形成LOD1～LODN共N个层次细节的模型。初始加载时，可以加载模型外壳（LOD1），随着视点的推进，逐步加载内层模型（LOD2～LODN）。
2.3 基于视锥体剔除的分层分段加载
如图1所示，针对建筑装饰专业模型尺寸大、构件面片数量多的情况，可以采用模型分层、分段的方式，将一个模型分拆成若干个子模型的组合。例如按楼层分拆，可以分为站厅层结构完成面、站台层结构完成面等5个子模型；按段分拆，可以将模型分为前、中、后3个部分。上传到服务器的RVT格式的模型经过分层、分段拆解，转换为GLB格式后集中存储。客户端加载模型时，需要提供当前视点对应的视锥体参数，模型服务器利用包围盒计算落在视锥体内的子模型，并将模型发送到客户端。
2.4 构件合并与减面
建筑装饰专业的模型经常存在大量连续铺设的墙砖、地砖、踢脚线。单个构件的面片数量很小（十几至几十个），然而连续铺设几千块地砖时，模型的面片数量可能达到几万至几十万。针对这类模型，轻量化的一个有效策略是进行构件的合并与减面。例如，可以在Blender软件中导入GLTF格式的模型，通过构件合并、减面、减顶点等操作，将大量独立的构件合并为一个整体，以此减小模型体量。
2.5 构件替换
如图1，在通信、给排水及消防专业的模型中，存在大量分散布置的构件，例如摄像机、消防栓、灭火器。这类构件外形复杂、面片数量很多，且分布于模型的不同部位，不宜采用减面、合并策略。比较有效的轻量化方法是在模型中找到同一类构件，利用规则的几何对象（长方体、圆柱体、棱锥体等）替换原构件。当相机视点逐渐接近构件时，采用LOD技术加载构件的原始模型。
2.6 BIM模型本地缓存
BIM模型文件一般存储在云端模型服务器上，客户端根据用户的浏览需求动态从服务器请求加载模型。基于服务器的加载方案有利于模型的集中管理、更新和发布。随着请求模型的客户端数量的增长、广域网模型传输时延不断增加，该方案会导致模型加载时间过长，降低用户体验。有效的解决方案是首次加载模型后，将模型数据缓存在客户端本地。
3 加载及渲染优化方法
依据上文的轻量化策略，可在模型加载前对其进行离线优化；而当模型大小不能进一步优化时，需要采取如下策略。
3.1 基于IndexDB的模型缓存与加载优化
本文采用IndexDB技术进行模型的本地缓存。IndexDB是目前主流浏览器广泛支持的一个轻量化非关系型数据库，各种类型的数据（字符串、二进制、Blob 对象）都可以采用“键值对”方式直接存入其对象仓库，且其没有最大存储容量限制，可以实现复杂查询、事务处理、游标和索引，避免网页卡顿。
3.1.1 模型缓存数据组织
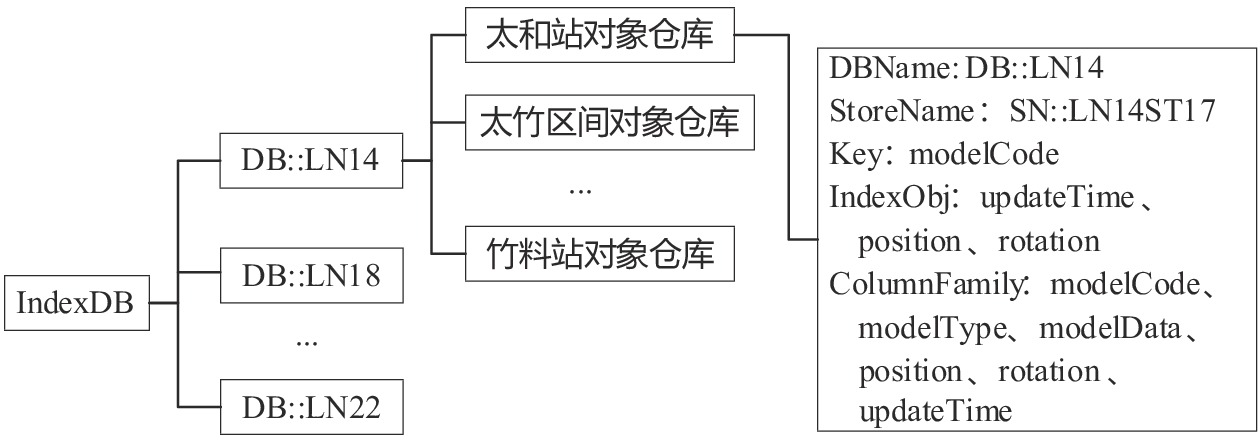
为了提高BIM模型数据存储和检索效率，为每一条地铁线路创建一个独立的数据库，如图2所示。
数据库命名规则为DB::线路编码。在数据库中，一个站点（车站、停车场、区间等）创建一个对象仓库，仓库命名定义为SN::站点编码。对象仓库以“键值对”方式存储模型数据。其中，Key为BIM模型编码（modelCode），Value包含模型编码（modelCode）、模型文件类型（modelType）、模型对象Blob （modelData）、更新时间（updateTime）、加载位置（position）、角度（rotation）共6列数据。为了便于模型检索，将模型更新时间、位置、角度定义为索引。
3.1.2 本地模型加载优化方案
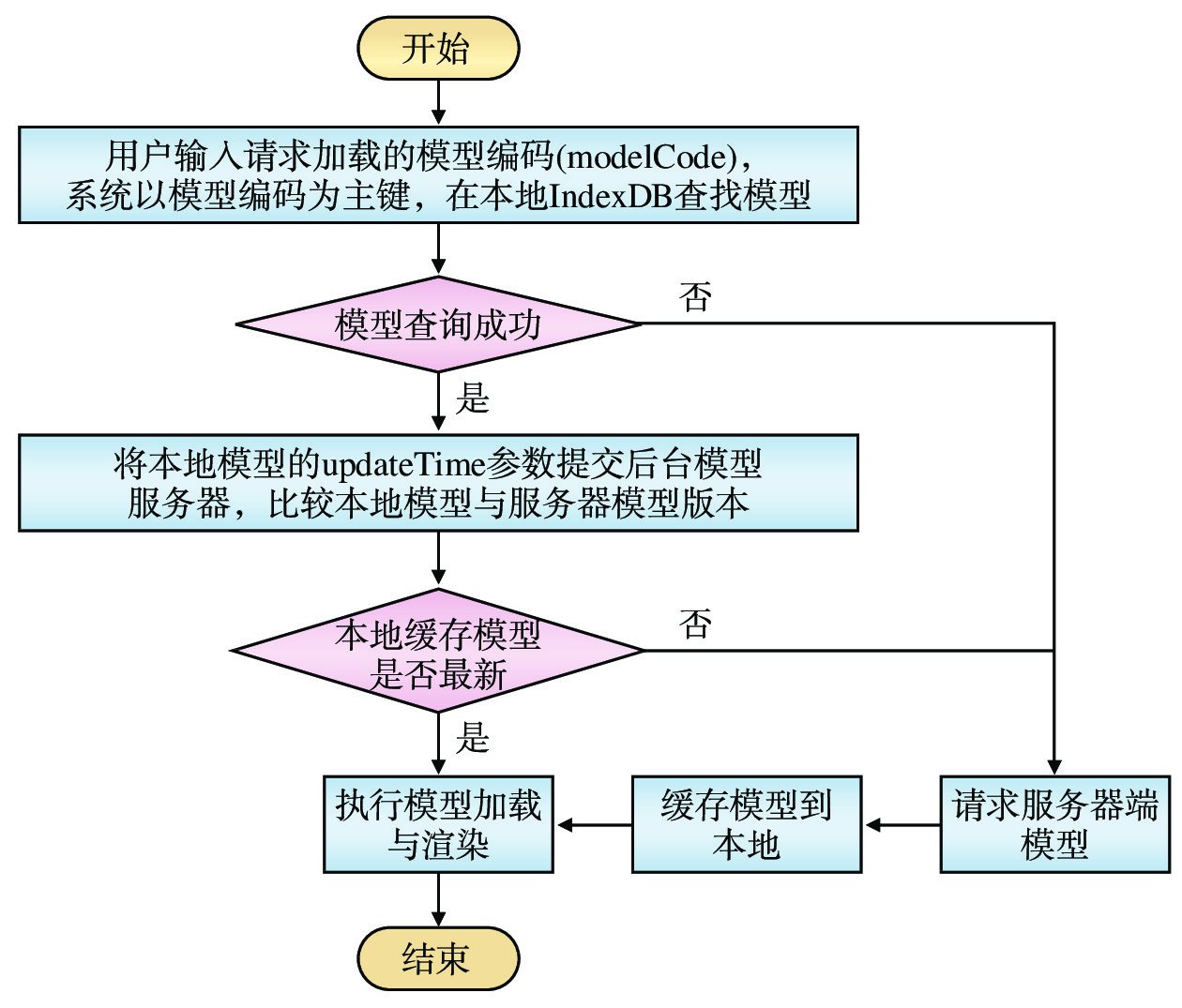
针对IndexDB模型缓存的数据组织，本文设计了一个模型加载的优化方案，如图3所示。
客户端加载模型时，首先会以modelCode为主键，从本地IndexDB查询是否存在该模型的本地缓存数据。如果存在本地缓存的模型，以updateTime为版本号，比较本地与远程服务器版本是否一致。如果本地模型版本较新，则直接加载本地模型。否则请求并渲染远程服务器的模型，同时将最新版本缓存到本地。由于前端JavaScript程序可以利用Web Worker执行异步操作，这里服务器端的模型渲染与缓存可以同时执行，不会导致浏览器卡顿。
3.2 基于视锥体剔除的渲染优化
地铁各专业模型的复杂程度和体量相差较大，大部分专业的模型采用前面的轻量化策略处理并缓存到本地后，可以满足模型加载渲染的需求。然而针对建筑装饰专业、多专业协同这类大规模渲染场景，离线模型轻量化策略仍略显不足。本节提出一个基于视锥体包围球的构件剔除算法，可以动态减小构件加载数量，提高浏览器渲染帧率。
3.2.1 包围球的构建
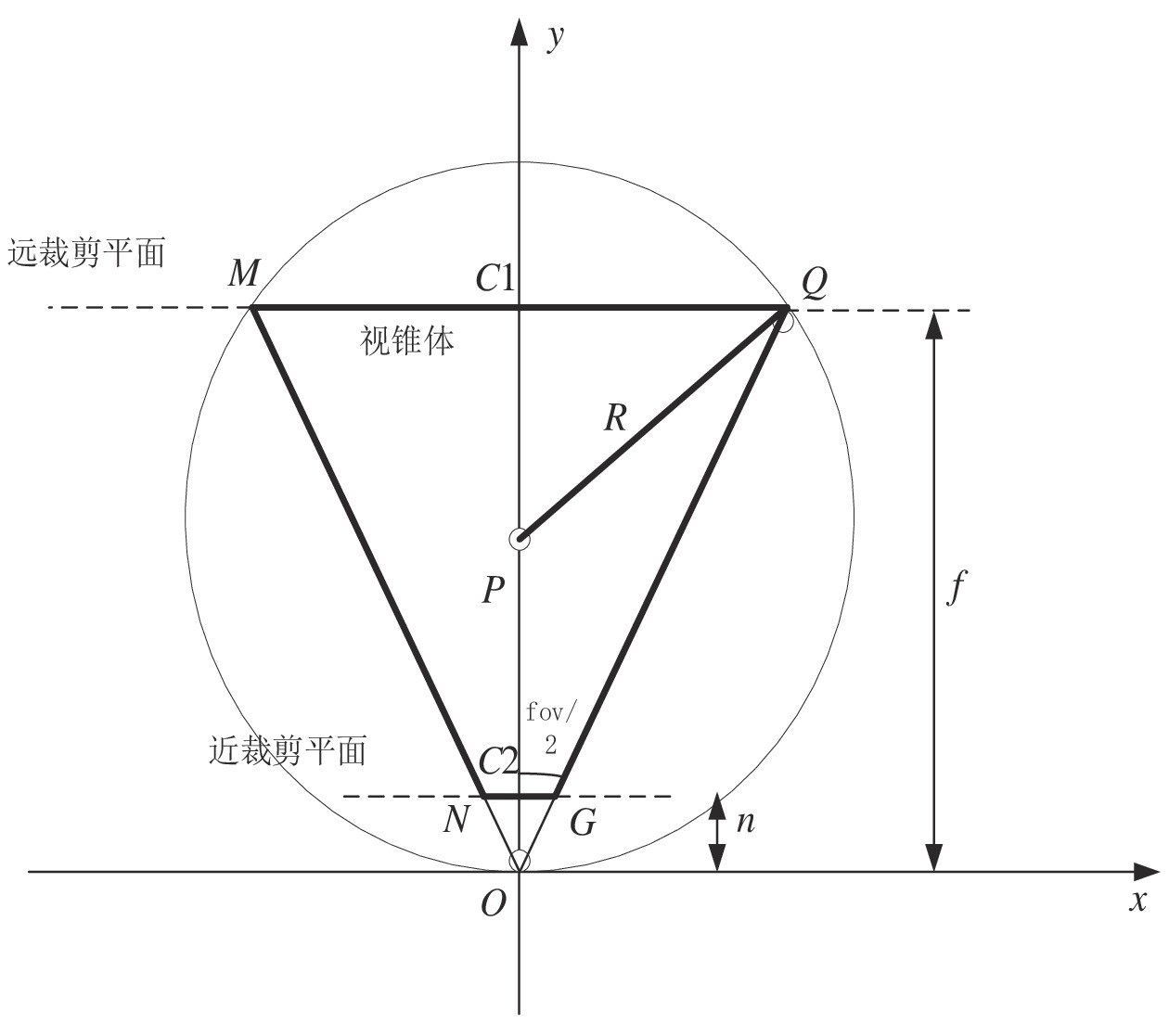
视锥体剔除是一种可见性剔除算法，其核心思想是将相机视锥体以外的构件直接剔除，避免渲染管线的无效渲染[7-8]。视锥体是指一个由上截面、下截面、左截面、右截面、近截面以及远截面共6个平面构成的一个封闭锥体。传统的视锥体剔除算法可以实现构件剔除，但需要将构件的所有顶点与视锥体的6个平面进行运算，其运算量庞大，因此有必要对视锥体剔除算法进行优化。本文提出基于包围球的快速视锥体剔除算法，包围球俯视图示意如图4所示。
在视锥体NGQM中，C1为远裁剪平面MQ的中点，C2为近裁剪平面NG的中点，取C1、C2连线的中点P作为视锥体包围球的球心，取PQ的距离R作为视锥体包围球的半径可以构建一个视锥体的包围球。原点O为相机视点所在位置，视点到视锥体近裁剪平面距离为n，到视锥体远裁剪平面距离为f，实际视场角为fov，包围球计算方法如下。
P点坐标为（0，Py），Py满足
$$ {P_y} = \frac{{f - n}}{2} + n = \frac{{f + n}}{2} $$ (1) Q点坐标为（Qx，Qy），由图4可知，Qy=f，Qx由三角函数可得
$$ \frac{{{Q_x}}}{f} = \tan \left( {\frac{{fov}}{2}} \right) \Rightarrow {Q_x} = f \cdot \tan \left( {\frac{{fov}}{2}} \right) $$ (2) 因此，P点坐标可表示为（0，（f+n）/2），Q点坐标表示为（f，f · tan（fov/2））。P点到Q点的距离即为视锥体包围球的半径R，根据两点间距离公式，可得
$$ {{R}} = \sqrt {{f^2} + {{\left( {f \cdot \tan \left( {\frac{{fov}}{2}} \right) - \frac{{f + n}}{2}} \right)}^2}} $$ (3) 将P点坐标转换到全局坐标系中，球心P及半径R两个系数可表示视锥体包围球。
3.2.2 基于包围球的快速视锥体剔除渲染方法
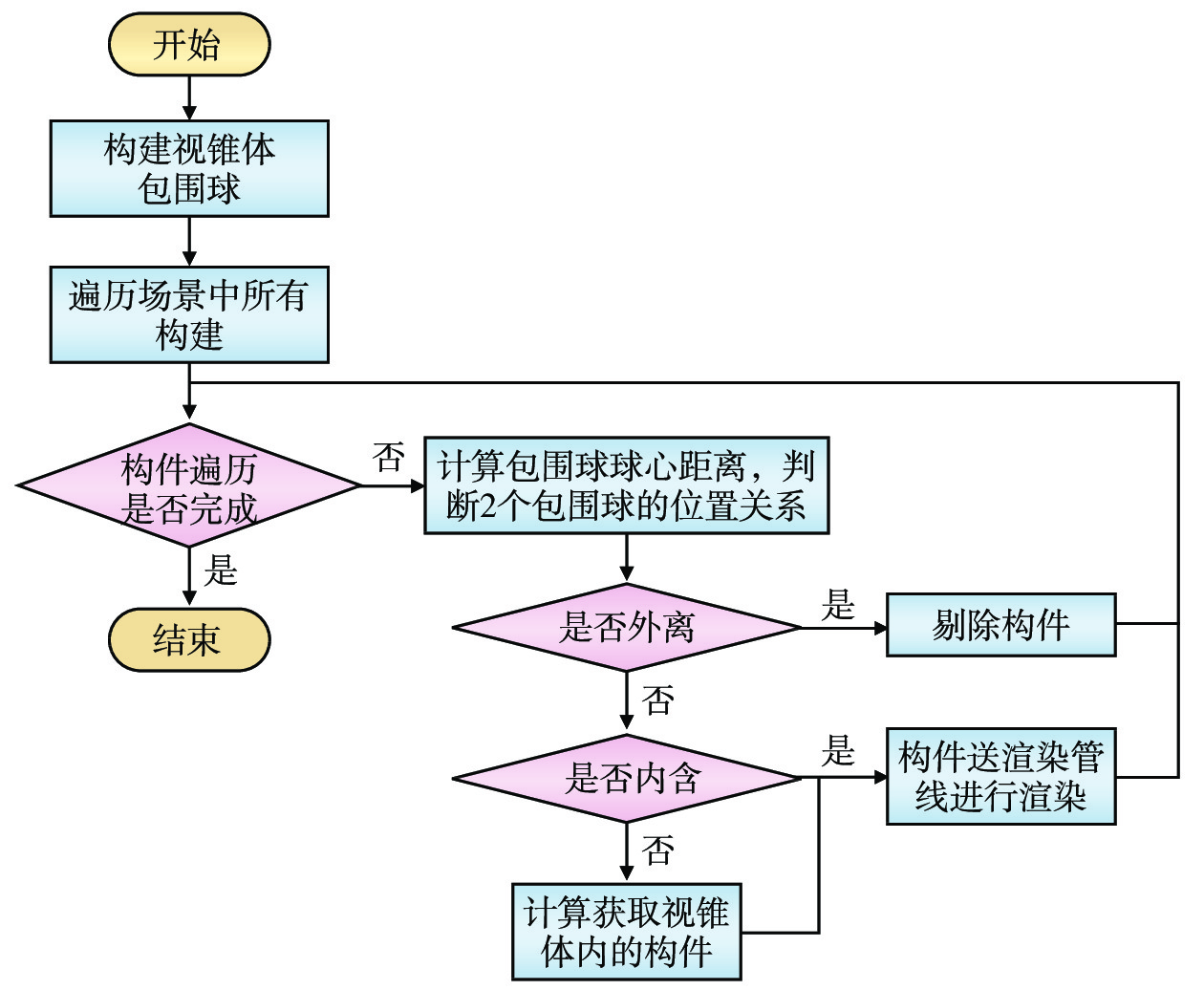
在BIM模型渲染场景中，视锥体包围球与构件包围球存在3种空间位置关系：（1）外离，即视锥体包围球与构件包围球不相交，此时视锥体包围球球心与构件包围球球心之间的距离大于两者半径之和；（2）相交，视锥体包围球与构件包围球有部分重叠，此时视锥体包围球球心与构件包围球球心之间的距离大于半径之差，小于半径之和；（3）内含，即构件包围球在视锥体包围球内部，此时视锥体包围球球心与构件包围球球心之间的距离小于两者半径之差。
针对上述3种关系，本文设计一个基于视锥体包围球的构件剔除算法，流程如图5所示。由于算法将视锥体的构件剔除转换为2个包围球位置关系判定，运算上降低了计算复杂度，有效提高了渲染效率。
4 实例验证
4.1 实验运行环境
实验采用了1台客户机，2台BIM模型服务器，其中，1台部署在云服务器上，用于测试BIM模型在广域网中传输的时延；另1台部署在本地，用来验证视锥体剔除算法。客户机与服务器平台配置如表2所示。
表 2 客户机与服务器平台配置名称 客户机参数 局域网服务器参数 云服务器参数 操作系统 Windows10 企业版 Windows10 企业版 Windows 2019 数据中心版 处理器型号 Intel Core i7-2802QM Intel Core i7-6700HQ Intel Xeon Platinum 8269CY 处理器规格 2.3 GHz/4核/8线程 2.6 GHz/4核/8线程 2.5 GHz/2核/4线程 内存大小 16 G 8 G 4 G 显卡型号 NVIDIA Quadro 1000M NVIDIA GTX960M 虚拟主机显卡 显存大小 2 G 2 G - 浏览器版本 Chrome 98.0.4758.82 - - 4.2 实验模型数据及结果分析
选择建筑装修与通风空调2个专业的模型进行加载优化与渲染优化的对比测试。
（1）模型缓存与加载优化方案测试
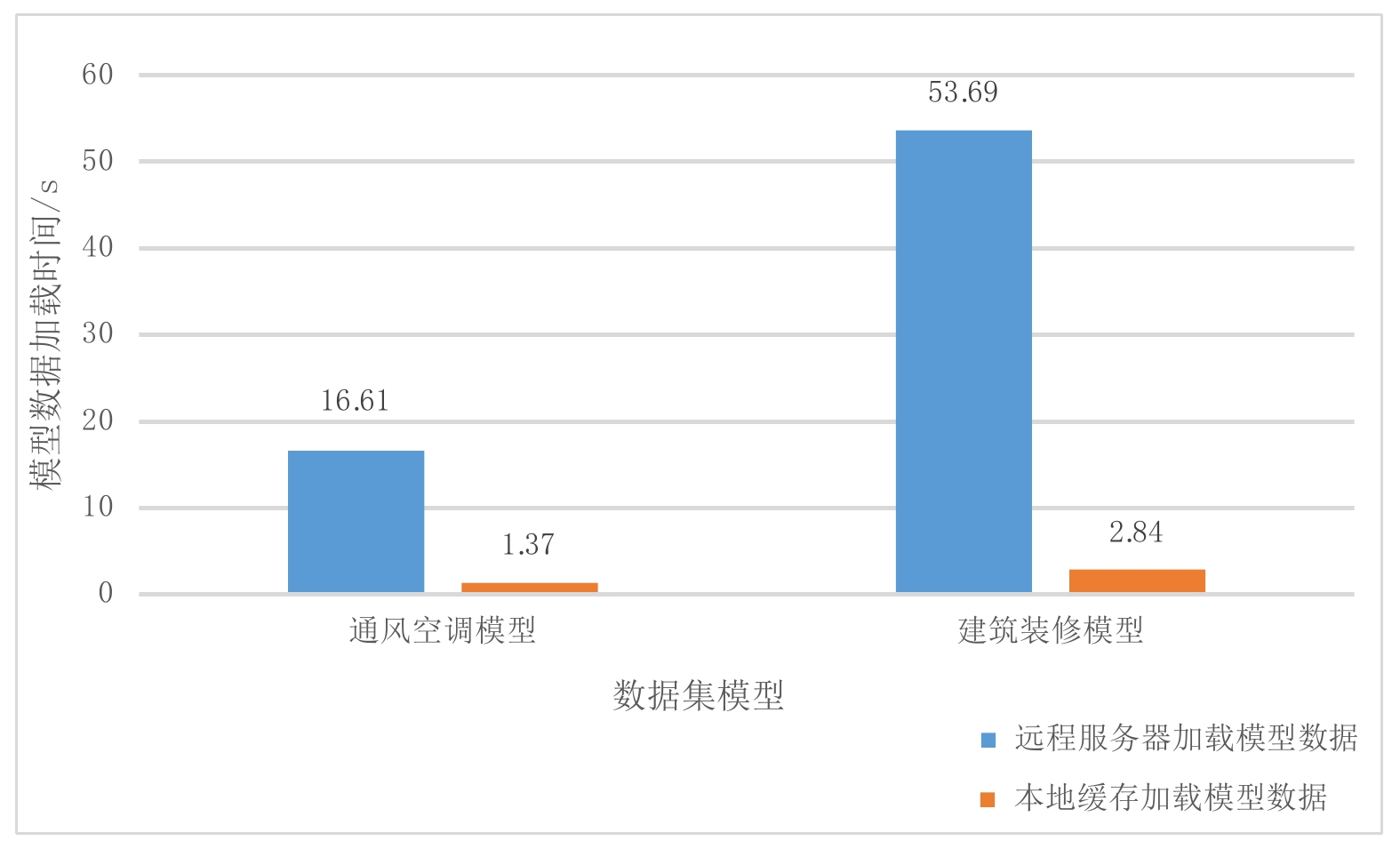
如图6所示，通风空调模型从远程服务器加载模型数据需要用时16.61 s，将数据存储到客户端本地缓存后，从本地缓存中直接加载模型数据的时间降低到了1.37 s；建筑装修模型采用了加载优化方案后，其模型加载时间也从53.69 s下降到了2.84 s。
（2）视锥体剔除渲染方法对比测试
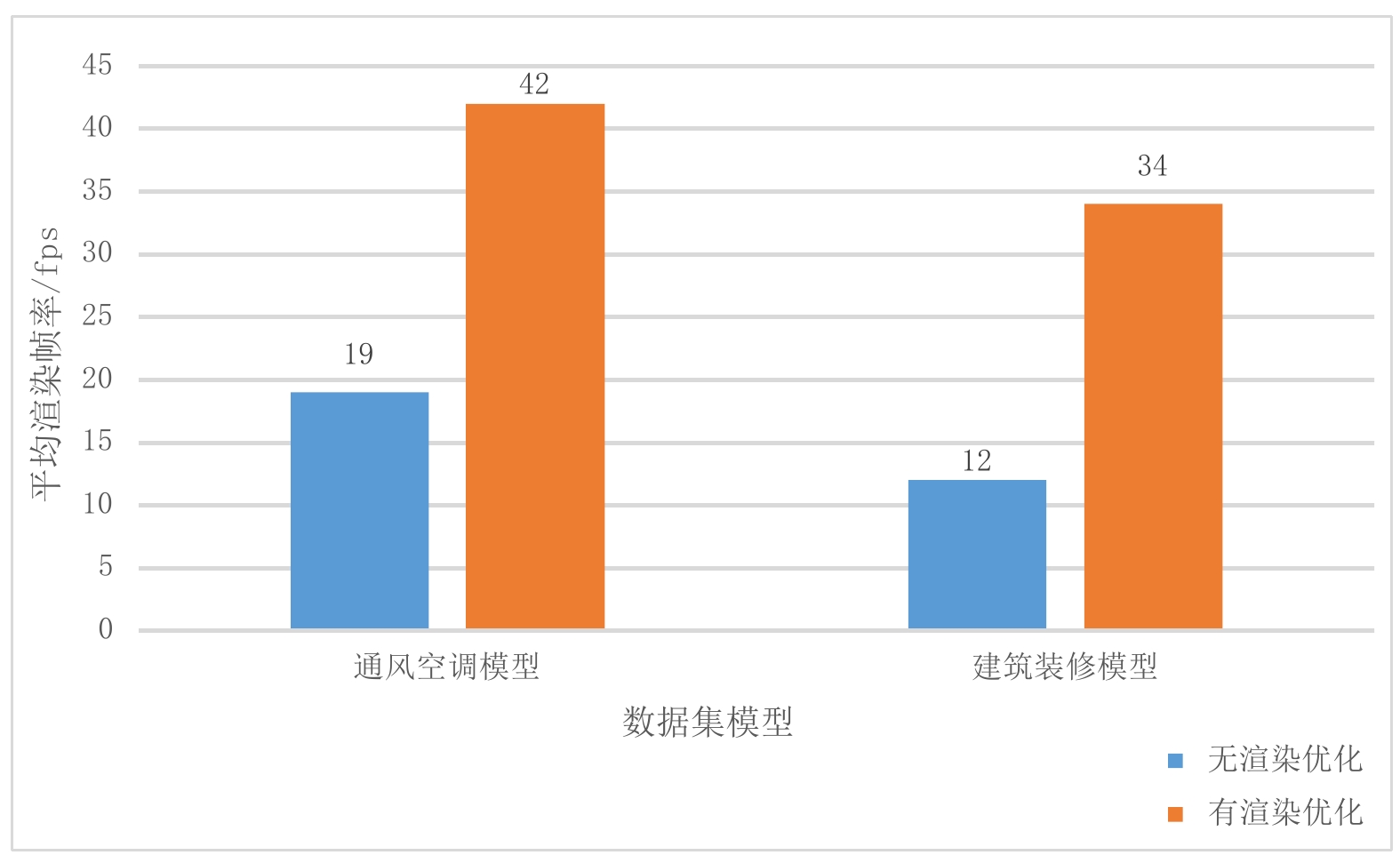
如图7所示，在没有采用包围球视锥体剔除算法时，通风空调模型的平均渲染帧率只有19 fps，浏览器渲染明显卡顿。引入包围球视锥体剔除算法后，模型的渲染帧率提升到了42 fps，平均提高了1.2倍。同样的，建筑装修模型采用了包围球视锥体剔除算法后，其渲染帧率也由平均12 fps提升到了34 fps，用户交互的流畅度得到了明显的改善。
5 结束语
针对地铁BIM模型构件多、体量大，浏览器端加载、渲染用户等待时间长、浏览器卡顿、页面崩溃等问题，本文提出了若干模型离线轻量化策略，有效降低了模型的复杂度。在此基础上，提出了模型加载优化及视锥体剔除优化方案，为BIM模型轻量化引擎开发作出了有益的探索。
-
表 1 地铁线路不同专业BIM模型体量对比
专业 模型大小/M 构件数量 顶点数量 面片数量 RVT IFC GLB 建筑装修 519 301 127 57 360 12 390 176 4 130 058 通风空调 51.2 122 54.1 10 125 2 657 562 885 854 给排水及消防 53.4 43.4 25.1 3 042 686 781 468 495 土建结构 63.6 16.4 6.5 1 164 164 528 117 964 通信系统 30.3 6.9 1.4 784 33 030 24 245 
下载: 导出CSV
表 2 客户机与服务器平台配置
名称 客户机参数 局域网服务器参数 云服务器参数 操作系统 Windows10 企业版 Windows10 企业版 Windows 2019 数据中心版 处理器型号 Intel Core i7-2802QM Intel Core i7-6700HQ Intel Xeon Platinum 8269CY 处理器规格 2.3 GHz/4核/8线程 2.6 GHz/4核/8线程 2.5 GHz/2核/4线程 内存大小 16 G 8 G 4 G 显卡型号 NVIDIA Quadro 1000M NVIDIA GTX960M 虚拟主机显卡 显存大小 2 G 2 G - 浏览器版本 Chrome 98.0.4758.82 - -
下载: 导出CSV
-
[1] 解亚龙,马西章,孟 飞. 铁路BIM工程化实施策略研究 [J]. 铁路计算机应用,2021,30(2):35-39. [2] 马 弯. BIM技术在鲁南铁路轨道设计中的应用 [J]. 铁路计算机应用,2019,28(6):50-53. DOI: 10.3969/j.issn.1005-8451.2019.06.012 [3] 李雅敬. 3D大模型的轻量级Web展示关键技术研究[D]. 上海: 同济大学, 2019. [4] 陈 前,王 玮. BIM模型轻量化及三维显示关键技术研究 [J]. 广东土木与建筑,2022,29(2):1-5. [5] 曹祎楠. 融合BIM与GIS的三维空间数据可视化研究[D]. 北京: 北京建筑大学, 2020. [6] Paligu F, Kumar A, Cho H, et al. BrowStExPlus: a tool to aggregate indexedDB artifacts for forensic analysis [J]. Journal of Forensic Sciences, 2019, 64(5): 1370-1378. DOI: 10.1111/1556-4029.14043
[7] Wang HW, Xiao L, Cao Y, et al. Visibility-culling-based geometric rendering of large-scale particle data[C]//2016 International Conference on Virtual Reality and Visualization (ICVRV). Hangzhou: IEEE, 2016: 197-203.
[8] Su M, Guo RF, Wang HL, et al. View frustum culling algorithm based on optimized scene management structure[C]//2017 IEEE International Conference on Information and Automation (ICIA). Macao, China: IEEE, 2017: 838-842.
-
期刊类型引用(1)
1. 梁潇，韩先峰，白云. BIM云渲染平台建设及其应用研究. 土木建筑工程信息技术. 2024(02): 46-51 . 
百度学术
其他类型引用(1)
计量
- 文章访问数: 66
- HTML全文浏览量: 91
- PDF下载量: 12
- 被引次数: 2
