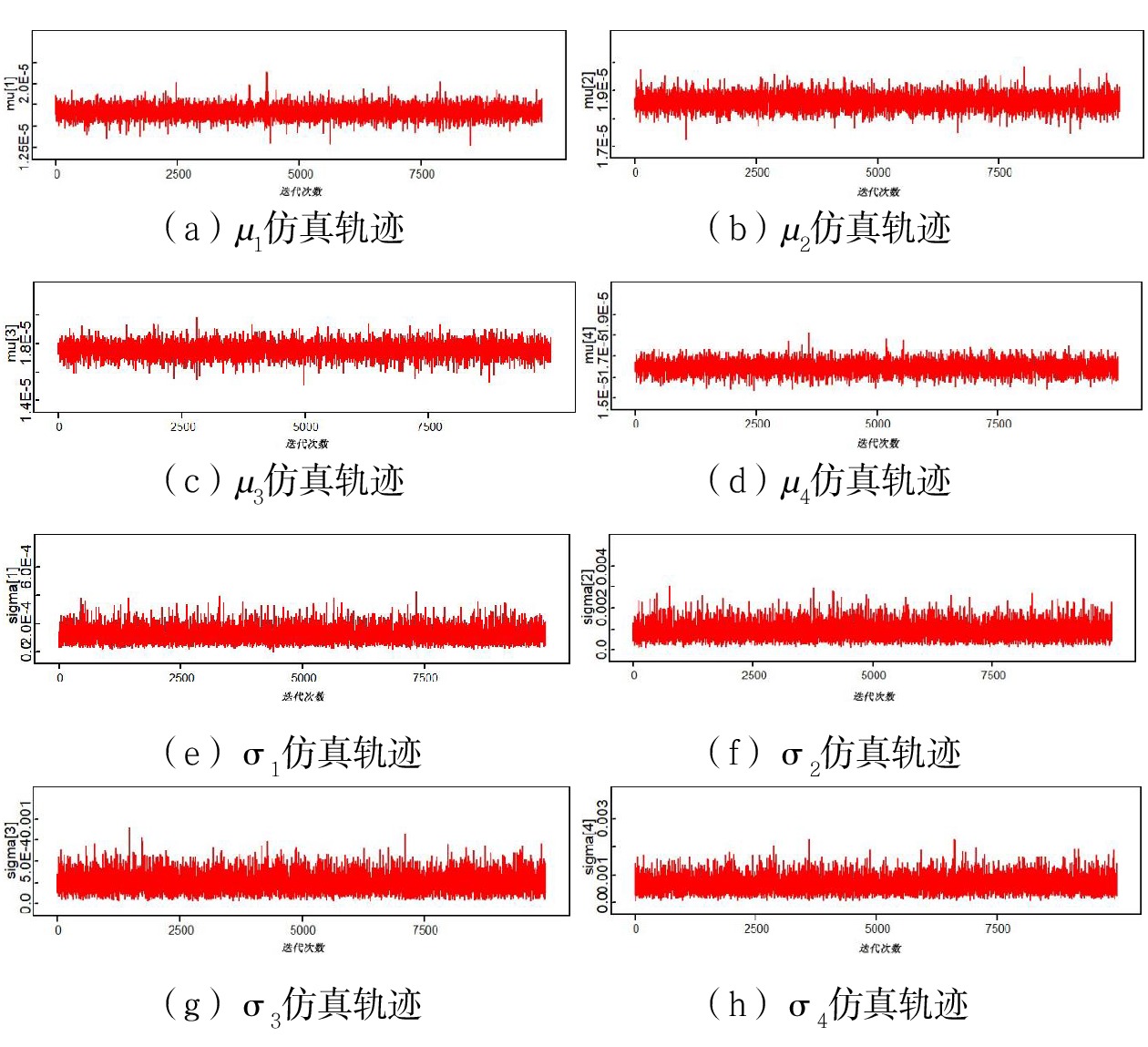
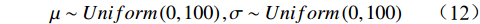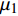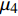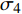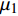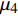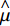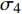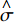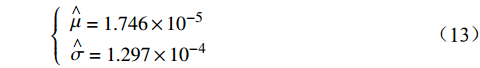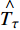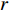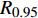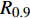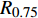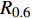Wheelset reliability evaluation of urban rail transit vehicles based on Wiener process
-
摘要: 为探究城市轨道交通(简称:城轨)车辆轮对的轮径值退化规律,有效评估轮对可靠性,提出基于Wiener过程的城轨车辆轮对可靠性评估方法。选取轮径值作为性能退化指标,建立基于Wiener过程的城轨车辆轮对退化模型。通过计算轮对剩余寿命,选择精度最高的退化模型进行可靠性评估。针对退化模型参数后验分布计算公式较为复杂的问题,采用马尔可夫链蒙特卡洛(MCMC,Markov Chain Monte Carlo)方法进行求解。 基于广州地铁8号线列车轮对实测数据进行实例验证,结果表明,城轨车辆应保证轮对可靠度不低于0. 9,且在镟修后运行至27.51万km时,应检查轮对退化情况,以保障车辆的运行安全。
-
关键词:
- 城市轨道交通 /
- Wiener过程 /
- 退化模型 /
- 可靠性评估 /
- 马尔可夫链蒙特卡洛(MCMC)方法
Abstract: In order to explore the degradation law of wheel diameter value of urban rail vehicle wheelsets and effectively evaluate the reliability of wheelsets, this paper proposed a wheelsets reliability evaluation method of urban rail transit vehicles based on Wiener process. The paper selected the wheel diameter value as the performance degradation index, and established the wheelset degradation model of urban rail vehicles based on the Wiener process. By calculating the remaining life of the wheelset, the paper selected the degradation model with the highest accuracy to evaluate the reliability. Aiming at the complex problem of calculating the posterior distribution formula of the parameters of the degradation model, the paper used the Markov chain Monte Carlo (MCMC) method to solve the problem. Based on the actual measurement data of the wheel sets of trains on Guangzhou Metro Line 8, the verification results show that urban rail vehicles should ensure that the reliability of the wheel sets is not less than 0 9. After turning and running to 275 100 km, the degradation of the wheel set should be checked to ensure the safe operation of the vehicle. -
城市轨道交通(简称:城轨)凭借其安全、便捷和舒适等特点,在城市综合交通中的重要程度日益提升,其运营维护也面临着更高的要求。轮对作为城轨车辆走行部的核心部件,其稳定性与可靠性直接影响着城轨车辆的安全运行。因此,针对城轨车辆轮对的可靠性研究具有重要的理论意义及社会价值。
在轮对寿命预测方面,田丽等人[1]对预处理后的轮径磨耗数据与运行里程进行线性拟合,以此预测轮对剩余寿命;叶正君等人[2]采用高阶多项式拟合曲线,建立了轮对寿命预测模型,在分析大量实测数据的基础上,得出轮对磨耗规律,对轮对全生命周期做出预测。 在镟修策略制定方面,张宇等人[3]选取车轮踏面磨耗量作为研究对象,分别利用线性回归模型和非线性回归神经网络进行建模,实现了轮对踏面退化状态预测,避免了轮对踏面的过度镟修;曾隆隆[4]通过分析城轨车辆轮对运营数据及镟修情况,得出城轨车辆左右侧轮对不存在偏磨现象的结论,优化了轮对镟修策略,延长了轮对使用寿命; 陶波[5]通过分析广州市城轨交通三号线列车轮对数据超标的原因及特点,提出了一种减少维修次数的轮对镟修模式。上述研究工作利用丰富的现场实测数据,建立了轮对寿命预测模型并对镟修策略进行了优化,但并未考虑轮对参数退化状态对轮对可靠性的影响。
目前,对于轮对退化规律的研究相对较少。 张义民等人[6]提出一种基于非平稳Gamma过程的机车车轮镟修里程预测方法,选取机车车轮轮缘厚度值作为性能退化指标,建立了退化模型,对轮对的镟修里程进行了预测; 吕昊等人[7]在此基础上,运用Copula函数提出了轮缘退化及滚动圆退化的相关可靠性预测方法,研究了镟修周期为20万km的车轮退化过程的可靠性。 上述文献以轮对轮缘为研究对象,对其退化规律进行了详细分析。 轮径值是否到限作为制定轮对镟修策略的另一重要因素,分析其退化规律同样具有重要意义,但目前鲜有单独针对城轨车辆轮径值退化规律的研究。
综上,本文选取轮径值作为性能退化指标,建立基于Wiener过程的城轨车辆轮对退化模型,结合现场经验与实测数据,对单个镟修周期内轮径值失效阈值进行假设。利用OpenBUGS软件实现马尔可夫链蒙特卡洛(MCMC ,Markov Chain Monte Carlo)方法,对模型参数的后验估计进行求解。 计算不同失效阈值情况下,轮对的平均剩余寿命,经过对比选取预测精度最高的退化模型,并进行可靠性评估。
1 基于Wiener过程的城轨车辆轮对退化模型
1.1 Wiener过程模型
轮对的退化过程是一个单调过程。在可靠性背景下,Wiener过程可描述产品在较短时间间隔内,性能指标随时间小幅增加或减少的特质。 因此,Wiener过程可以很好地描述轮对的退化过程。Wiener过程可表示为
$$ X\left( t \right) = {x_0} + \mu t + \sigma W\left( t \right) $$ (1) 其中,
$ {x_0} $ 是初始退化量,为考虑退化过程的一般性,通常设为0;$ \mu $ 是反映退化速率的漂移参数;$ \sigma $ 是扩散参数;$ t $ 是单调递增的时间;$ W\left( t \right) $ 表示退化过程中随机动态的标准布朗运动过程。1.2 模型建立
假设性能退化量
$ P\left( t \right) $ 的退化过程$ \left\{ {P\left( t \right),t > 0} \right\} $ 服从Wiener过程,则$ P\left( t \right) $ 具有如下性质[8](1)
$P\left( 0 \right) = 0$ ;(2)
$ P\left( t \right) $ 具有独立增量$\Delta P\left( t \right) = P\left( {t + \Delta t} \right) - P\left( t \right)$ ;(3)时刻
$ t $ 到$ t + \Delta t $ 间的独立增量$\Delta P\left( t \right)$ 服从均值为$ \mu \Delta t $ 和方差为$ {\sigma ^2}\Delta t $ 的正态分布,表示为$\Delta P \sim {{N}}( {\mu \Delta t,{\sigma ^2}\Delta t} )$ 。基于性能退化进行寿命分析时,通常将寿命
$ T $ 定义为性能参数首次到达失效阈值时的时间(简称:首达时间),指定$ L $ 为城轨车辆轮对轮径值的失效阈值,基于退化过程$ P\left( t \right) $ 的首达时间$ T $ 可表示为$$ T = \inf \left\{ {t:P\left( t \right) \geqslant L|P\left( 0 \right) \leqslant L} \right\} $$ (2) 根据Wiener过程的基本性质可得,首达时间
$ T $ 服从逆高斯分布$T \sim {{IG}}\left( {\dfrac{L}{\mu },\dfrac{{{L^2}}}{{{\sigma ^2}}}} \right)$ ,其对应的概率密度函数与累计函数为$$ {f_T}\left( t \right) = \frac{L}{{\sqrt {2{\text{π}} {\sigma ^2}{t^3}} }}\exp \left( { - \frac{{{{\left( {L - \mu t} \right)}^2}}}{{2{\sigma ^2}t}}} \right) $$ (3) $$ {F_T}\left( t \right) = \varPhi \left( {\frac{{\mu t - L}}{{\sigma \sqrt t }}} \right) + \exp \left( {\frac{{2\mu L}}{{{\sigma ^2}}}} \right)\varPhi \left( {\frac{{ - L - \mu t}}{{\sigma \sqrt t }}} \right) $$ (4) 由公式(3)可知,城轨车辆轮对可靠度函数为
$$ \begin{gathered} R\left( {t|\mu ,\sigma } \right) = 1 - {F_{IG}}\left( {t|\mu ,\sigma } \right) \\ {\text{ }} = \varPhi \left( {\frac{{L - \mu t}}{{\sigma \sqrt t }}} \right) + \exp \left( {\frac{{2\mu L}}{{{\sigma ^2}}}} \right)\varPhi \left( { - \frac{{L + \mu t}}{{\sigma \sqrt t }}} \right) \\ \end{gathered} $$ (5) 设城轨车辆运行到
$ \tau $ 时刻时,轮对累计轮径退化量为$ {x_\tau }({x_\tau } \leqslant L) $ ,根据Wiener过程的齐次马尔可夫性质,城轨车辆轮对的剩余寿命$ {T_\tau } $ 为$$ {T_\tau } = \inf \left\{ {t:P\left( t \right) \geqslant L - {x_\tau }|P\left( 0 \right) \leqslant L} \right\} $$ (6) 由公式(5)可知,城轨车辆轮对剩余寿命
$ {T_\tau } $ 也服从逆高斯分布,其概率密度函数为$$ {f_{{T_\tau }}}\left( t \right) = \frac{{L - {x_\tau }}}{{\sqrt {2{\text{π}} {\sigma ^2}{t^3}} }}\exp \left( { - \frac{{{{\left( {L - {x_\tau } - \mu t} \right)}^2}}}{{2{\sigma ^2}t}}} \right) $$ (7) 当求出退化模型参数后,轮轨车辆轮对的平均剩余寿命为
$$ \mathop {{T_\tau }}\limits^ \wedge = {\text{E}}\left( {{T_\tau }} \right) = \frac{{L - {x_\tau }}}{\mu } $$ (8) 2 基于贝叶斯理论的模型参数估计
2.1 退化数据的数学表达
通过测量得到某城轨车辆
$ N $ 个车轮的退化数据样本,该组车轮在离散时间$ M $ 内被观测,其中,$i = 1,2, \cdots ,N$ 为样本序号,$j = 1,2, \cdots ,M$ 为观测时间序号,定义$ \Delta {P_{ij}} = {P_{ij}} - {P_{i,j - 1}} $ 为第$ i $ 个样本车轮的退化增量,设初始时刻退化量$ {P_{i0}} = 0 $ , 由Wiener过程性质可得:退化增量$ \Delta {P_{ij}} $ 服从正态分布:$\Delta {P_{ij}} \sim {{N}}\left( {\mu \Delta {t_{ij}},{\sigma ^2}\Delta {t_{ij}}} \right)$ 且$\Delta {t_{ij}} = {t_{ij}} - {t_{i,j - 1}}$ 。 退化过程的似然函数可表示为$$ \begin{gathered} L\left( {P|\mu ,\sigma } \right) = \prod\limits_{i = 1}^N {\prod\limits_{j = 2}^M {f\left( {\Delta {P_{ij}}|\mu ,\sigma } \right)} } \\ {\text{ }} = \prod\limits_{i = 1}^N {\prod\limits_{j = 2}^M {\frac{1}{{\sqrt {2{\text{π}} {\sigma ^2}\Delta {t_{ij}}} }}\exp \left( { - \frac{{{{\left( {\Delta {P_{ij}} - \mu \Delta {P_{ij}}} \right)}^2}}}{{2{\sigma ^2}\Delta {P_{ij}}}}} \right)} } \\ \end{gathered} $$ (9) 其中,
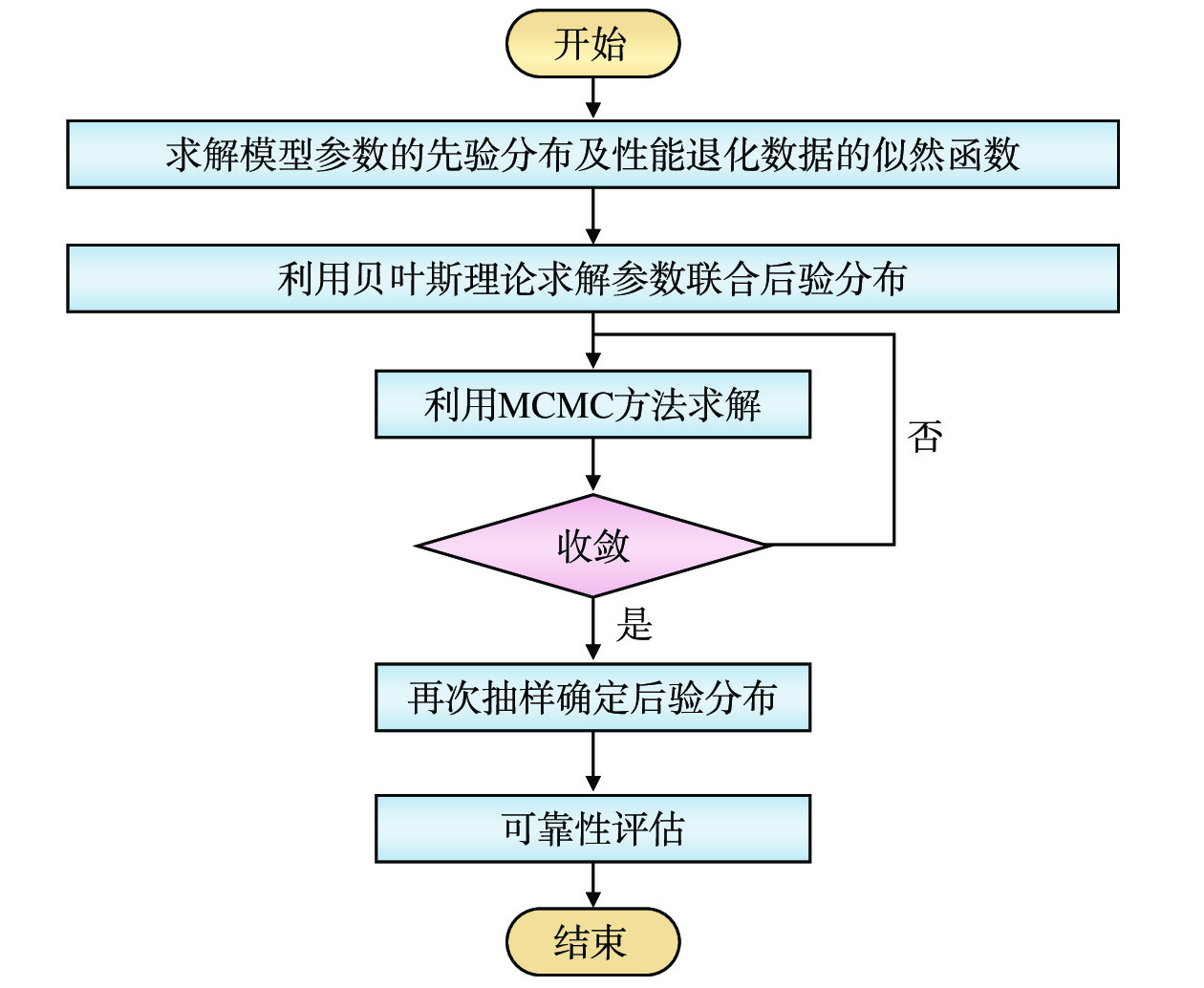
$ f\left(\Delta {P}_{ij}\mu ,\sigma \right) $ 为标准正态分布的概率密度函数。假定模型联合先验分布为
${{\pi}} \left( \theta \right) = {{\pi}} \left( {\mu ,\sigma } \right)$ ,根据贝叶斯理论,模型待估计参数的联合后验分布可表示为[9]$$ \begin{gathered} p\left( {\mu ,\sigma |D} \right) \propto {\pi} \left( \theta \right)L\left( {D|\mu ,\sigma } \right) \\ {\text{ }} = {\pi} \left( {\mu ,\sigma } \right)\prod\limits_{i = 1}^N {\prod\limits_{j = 2}^M {\frac{1}{{\sqrt {2{\text{π}} {\sigma ^2}\Delta {t_{ij}}} }}\exp \left( { - \frac{{{{\left( {\Delta {P_{ij}} - \mu \Delta {P_{ij}}} \right)}^2}}}{{2{\sigma ^2}\Delta {P_{ij}}}}} \right)} } \\ \end{gathered} $$ (10) 其中,D为观测样本数据集。由公式(6)和公式(8)可知,基于Wiener过程的城轨车辆轮对的可靠度函数为
$$ R\left( {n|D} \right) = \iint\limits_{\mu ,\sigma > 0} {p\left( {\mu ,\sigma |D} \right)R\left( {t|\mu ,\sigma } \right)} {\text{d}}\mu {\text{d}}\sigma $$ (11) 2.2 MCMC方法
公式(9)所述后验分布的计算公式较为复杂,因此,采用MCMC方法对其进行求解[10]。MCMC方法的基本思想是建立Markov链,对未知变量进行抽样模拟,当Markov链达到稳态分布时,即得所求后验分布。 其中一种常用的方法是Gibbs抽样方法[11],从给定数据与其他所有参数的条件后验分布进行模拟,可有效处理高维问题,并已广泛应用于可靠性评估。Gibbs抽样方法如下。
步骤1:选取任意一个初始点
${\theta ^{\left( 0 \right)}} = ( {\theta _{1,0}},{\theta _{2,0}}, \cdots , {\theta _{n,0}} )'$ ,设置$ i = 0 $ ;步骤2:按下列方法生成
${\theta ^{\left( {i + 1} \right)}} = ( {\theta _{1,i + 1}},{\theta _{2,i + 1}}, \cdots , {\theta _{n,i + 1}} )'$ ${\theta _{1,i + 1}} \sim {\pi} \left( {{\theta _1}|{\theta _{2,i}}, \cdots ,{\theta _{n,i}},D} \right)$ ,${\theta _{2,i + 1}} \sim {\pi} \left( {{\theta _2}|{\theta _{1,i + 1}},{\theta _{3,i}}, \cdots ,{\theta _{n,i}},D} \right)$ ,……
${\theta _{n,i + 1}} \sim {\pi} \left( {{\theta _n}|{\theta _{1,i + 1}},{\theta _{2,i + 1}}, \cdots ,{\theta _{n - 1,i + 1}},D} \right)$ ;步骤3:若 i 已达到设定的迭代次数,程序结束;否则,令 i自增1,返回至步骤1。
在Gibbs抽样过程中,按照自然顺序生成
$ \theta $ 的每个分量,每个循环产生$ n $ 个随机变量${\pi} \left(\theta | D\right)$ 是观察到数据集$ D $ 后,$ \theta $ 的后验分布。本文基于OpenBUGS软件实现MCMC方法。通过软件进行10 000次迭代,以获取模型后验分布与模型参数估计结果,进而对城轨车辆轮对进行可靠性评估。为降低主观信息干扰,模型参数统一采用均匀分布形式的无信息先验分布,以获取更为精确的参数估计结果。基于贝叶斯理论的轮径值退化数据分析及可靠性评估程序的流程,如图1所示,在求解模型参数先验分布及性能退化数据似然函数的基础上通过贝叶斯理论推导后验分布公式,再利用MCMC方法进行求解,并进行可靠性评估。
3 实例分析
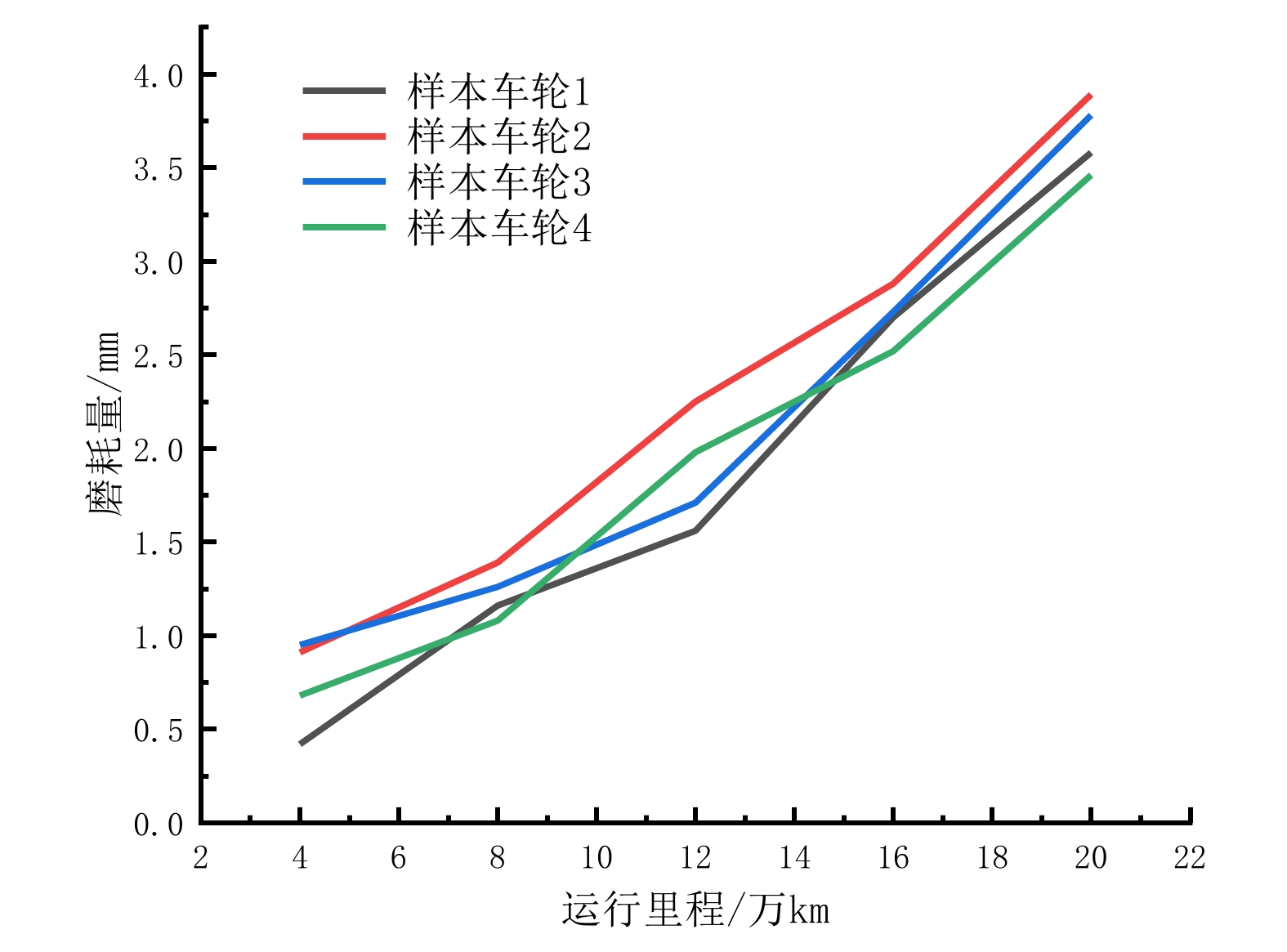
本文选取广州地铁8号线某列车车厢1号转向架轮对实测的退化数据进行验证计算[12]。退化数据为4个样本车轮分别在4 万km、8 万km、12 万km、16 万km、20万km处测得的轮径磨耗量。 由于人工测量误差及检测设备测量位置差异等原因,原始数据中出现了部分不符合轮对参数磨耗规律的情况。 因此,需先对原始数据进行预处理,预处理所得数据如图2所示。
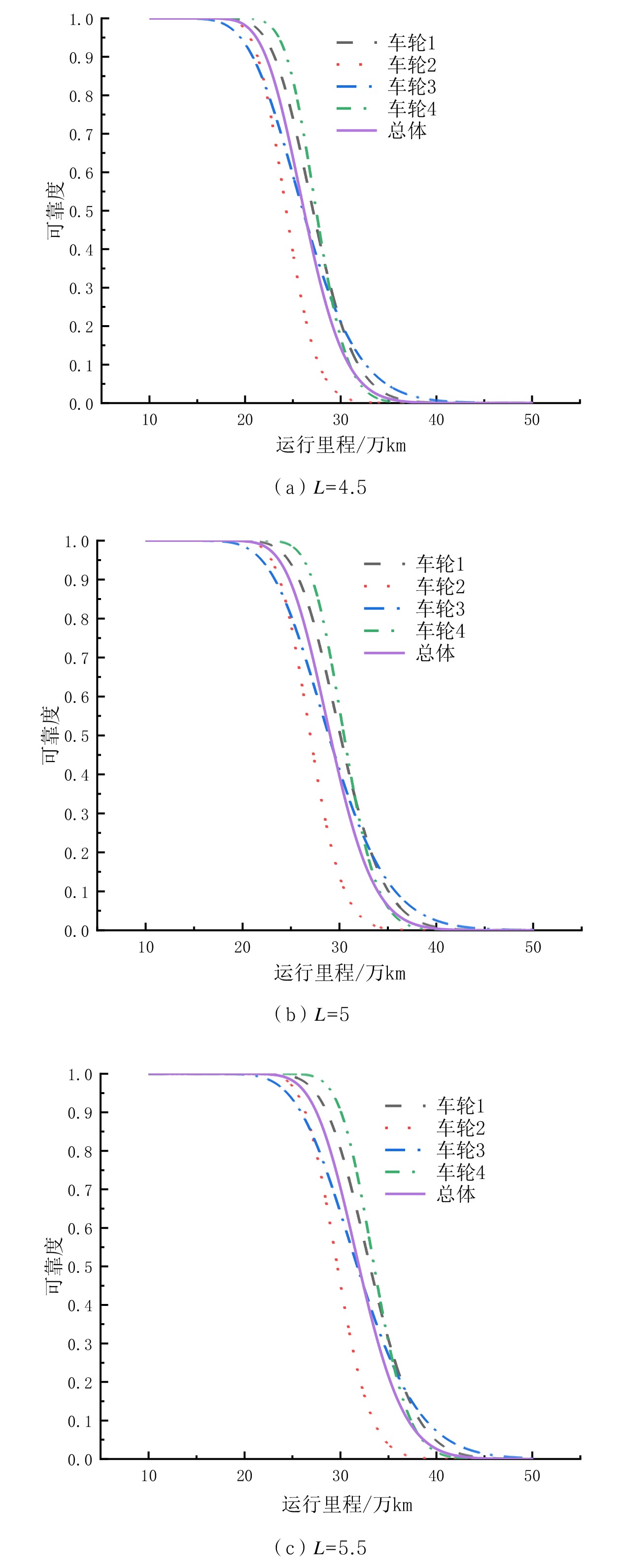
由图2可知,共测定4组样本车轮的轮径退化值。样本车轮的序号为i, i = 1, 2, 3, 4;μi 和 σi 分别为4组样本车轮的模型参数。 针对缺乏单个镟修周期内轮径值失效阈值信息的情况,本文通过结合现场经验及大量实测退化数据,假设出3个不同的轮径值作为退化过程失效阈值进行分析,分别为4. 5 mm、5 mm和5. 5 mm.
3.1 基于退化数据的模型参数估计
模型参数统一采用均匀分布形式的无信息先验分布,如公式(12)所示。
$$ \mu \sim Uniform\left( {0,100} \right),\sigma \sim Uniform\left( {0,100} \right) $$ (12) 参数的联合后验分布如公式(9)所示,通过OpenBUGS软件写入样本车轮退化数据,获取参数后验分布概率密度函数。 对于MCMC方法,在仿真过程中应确保抽样数据能够收敛于参数的后验分布。 模型参数仿真轨迹如图3所示,图3(a)~图3(d)、图3(e)~图3(h)分别给出了模型参数
$ {\mu _1} $ ~$ {\mu _4} $ 和$ {\sigma _1} $ ~$ {\sigma _4} $ 通过OpenBUGS软件进行10000次迭代后的仿真轨迹,图3中纵坐标均为参数估计值,可知数据并未出现显著不规律变化,即可认为模型各参数都具有较好的收敛性[13]。模型参数估计结果如表1所示,取
$ {\mu _1} $ ~$ {\mu _4} $ 的均值为$ \mathop \mu \limits^ \wedge $ ,$ {\sigma _1} $ ~$ {\sigma _4} $ 的均值为$ \mathop \sigma \limits^ \wedge $ 。表 1 模型参数估计值模型参数 统计特征值 均值 标准差 $ {\mu _1} $ 1. 673×10–5 6. 520×10–7 $ {\mu _2} $ 1. 861×10–5 2. 404×10–7 $ {\mu _3} $ 1. 754×10–5 4. 536×10–7 $ {\mu _4} $ 1. 647×10–5 2. 764×10–7 $ {\sigma _1} $ 1. 194×10–4 5. 112×10–5 $ {\sigma _2} $ 8. 867×10–5 3. 752×10–4 $ {\sigma _3} $ 2. 459×10–4 1. 048×10–4 $ {\sigma _4} $ 6. 495×10–5 2. 743×10–4 经计算
$$ \left\{\begin{array}{l} \mathop \mu \limits^ \wedge = 1.746\times 10^{-5} \\ \mathop \sigma \limits^ \wedge = 1.297\times10^{-4} \end{array} \right.$$ (13) 3.2 样本车轮可靠性评估
根据公式(9)及模型参数估计结果,对样本车轮个体与总体在不同失效阈值情况下进行可靠性评估,如图4所示。
由图4可知,样本车轮可靠度曲线在衰减至0.9后下降速度明显变快。另外,同转向架轮对由于加工、装配及左右车轮磨耗不同等不确定因素的影响,表现出的可靠性存在一定差异。对比样本总体与样本个体的可靠度曲线可知,总体的可靠度曲线基本处于所有样本车轮可靠度曲线的中间,这是由于对总体进行可靠度评估考虑了所有个体对应参数的不确定性,而各个样本的可靠性评估仅考虑本身参数的不确定性。
根据公式(8)及公式(13)计算不同阈值情况下样本车轮运行至20万km时平均剩余寿命预测值
$ \mathop {{T_\tau }}\limits^ \wedge $ ,结果如表2所示,失效阈值为5.5 mm的可靠性评估模型预测精度更高。同时,给出了失效阈值为5.5 mm的情况下,线性回归模型同本文模型的预测精度对比,如表3所示,可以看出,基于Wiener过程的退化模型相比线性回归模型预测精度更高。表 2 样本车轮平均剩余寿命预测值失效阈值/mm 预测值/万km 实际值/万km 相对误差/% 4. 5 4. 71 10 −52. 9 5 7. 57 10 −24. 3 5. 5 10. 44 10 4. 4 表 3 基于Wiener过程的可靠性评估模型与线性回归模型对比预测模型 预测值/万km 相对误差/% 线性回归模型 8. 19 −18. 1 基于Wiener过程的可靠性评估模型 10. 44 4. 4 一个轮对可靠度值
$ r $ 对应一个相应的列车运行里程,称为轮对的可靠寿命。表4是失效阈值为5.5 mm情况下样本车轮总体可靠寿命的计算结果,表4中$ {R_{0.95}} $ 、$ {R_{0.9}} $ 、$ {R_{0.75}} $ 、$ {R_{0.6}} $ 分别代表可靠度下降至0. 95、0. 9、0. 75、0. 6时样本车轮的总体可靠寿命。由表4可知,当样本车轮可靠度下降至0. 9时,其总体可靠寿命为27.51 万km。因此,为保证车辆运行安全,当列车运行里程达到27 万km时,应检查轮对退化情况,并制定相应镟修策略。表 4 样本车轮总体可靠寿命失效阈值/mm 可靠寿命/万km ${ {{R} }_{0.95} }$ ${ {{R} }_{0.9} }$ ${ {{R} }_{0.75} }$ ${ {{R} }_{0.6} }$ 5. 5 26. 38 27. 51 29. 52 31. 01 4 结束语
本文建立了基于Wiener过程的城轨车辆轮对退化模型,经计算,失效阈值为5.5 mm的模型预测精度最高,因此,选用该模型进行可靠性评估。 经分析,在一个镟修周期内,城轨车辆轮对可靠度衰减至0.9后下降速度明显变快,为保证车辆运行安全,应保证轮对可靠度不低于0.9,该情况下,轮对可靠寿命为27.51 万km,即城轨车辆应在轮对镟修后运行约27 万km时检查轮对退化情况,并制定相应镟修策略。
-
表 1 模型参数估计值
模型参数 统计特征值 均值 标准差 $ {\mu _1} $ 1. 673×10–5 6. 520×10–7 $ {\mu _2} $ 1. 861×10–5 2. 404×10–7 $ {\mu _3} $ 1. 754×10–5 4. 536×10–7 $ {\mu _4} $ 1. 647×10–5 2. 764×10–7 $ {\sigma _1} $ 1. 194×10–4 5. 112×10–5 $ {\sigma _2} $ 8. 867×10–5 3. 752×10–4 $ {\sigma _3} $ 2. 459×10–4 1. 048×10–4 $ {\sigma _4} $ 6. 495×10–5 2. 743×10–4 表 2 样本车轮平均剩余寿命预测值
失效阈值/mm 预测值/万km 实际值/万km 相对误差/% 4. 5 4. 71 10 −52. 9 5 7. 57 10 −24. 3 5. 5 10. 44 10 4. 4 表 3 基于Wiener过程的可靠性评估模型与线性回归模型对比
预测模型 预测值/万km 相对误差/% 线性回归模型 8. 19 −18. 1 基于Wiener过程的可靠性评估模型 10. 44 4. 4 表 4 样本车轮总体可靠寿命
失效阈值/mm 可靠寿命/万km ${ {{R} }_{0.95} }$ ${ {{R} }_{0.9} }$ ${ {{R} }_{0.75} }$ ${ {{R} }_{0.6} }$ 5. 5 26. 38 27. 51 29. 52 31. 01 -
[1] 田 丽,刘 森. 基于数据拟合的地铁车辆车轮磨耗分析与寿命预测 [J]. 铁道技术监督,2022,50(2):65-68. DOI: 10.3969/j.issn.1006-9178.2022.02.012 [2] 叶正君,张健雨,邢宗义,等. 轨道交通车辆轮对寿命预测及镟修优化策略 [J]. 城市轨道交通研究,2020,23(9):108-112. DOI: 10.16037/j.1007-869x.2020.09.024 [3] 张 宇,霍苗苗,陈 霞,等. 城市轨道交通车辆车轮踏面经济型镟修应用研究 [J]. 铁路计算机应用,2022,31(2):73-78. [4] 曾隆隆. 轨道交通车辆轮对磨耗特征分析与镟修策略优化 [J]. 装备机械,2021(3):42-46,50. [5] 陶 波. 广州市轨道交通三号线北延段列车轮对镟修策略研究 [J]. 电力机车与城轨车辆,2015,38(5):93-94. [6] 张义民,林禄样,吕 昊. 基于Gamma过程的机车车轮镟修里程预测方法 [J]. 东北大学学报(自然科学版),2018,39(4):522-526. [7] 吕 昊,金雄程,林录样. 基于Copula的车轮Gamma退化过程 [J]. 东北大学学报(自然科学版),2021,42(4):544-549,566. [8] Dai Y, Cheng S, Gan Q J, et al. Life prediction of Ni-Cd battery based on linear Wiener process [J]. Journal of Central South University, 2021, 28(9): 2919-2930. DOI: 10.1007/s11771-021-4816-5
[9] 宋兆理,贾 祥,郭 波,等. 基于贝叶斯融合与仿真的系统剩余寿命预测 [J]. 系统工程与电子技术,2021,43(6):1706-1713. [10] 朱晓荣,王羽凝,金绘民,等. 基于马尔科夫链蒙特卡洛方法的光伏电站可靠性评估 [J]. 高电压技术,2017,43(3):1034-1042. [11] Guan Q, Tang Y C, Xu A C. Reference Bayesian analysis of inverse Gaussian degradation process [J]. Applied Mathematical Modelling, 2019(74): 496-511. DOI: 10.1016/j.apm.2019.05.013
[12] 张健雨. 轨道交通车辆轮对全生命周期低成本运用优化研究[D]. 南京: 南京理工大学, 2019. [13] 彭卫文. 重型数控机床可靠性建模与评估技术研究[D]. 成都: 电子科技大学, 2016.




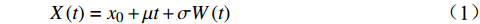
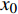
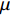
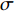
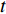
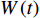
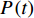
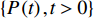
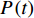
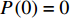
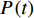
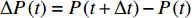
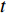
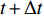
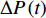
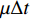
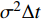
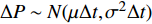
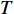
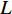
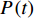
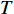
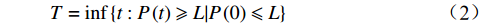
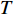
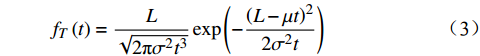
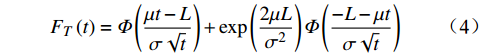
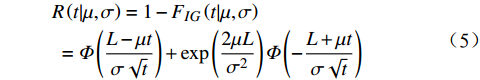
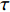
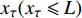
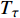
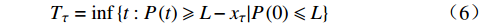
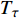
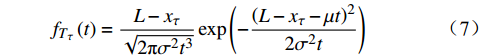

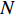
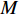
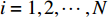
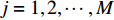
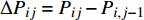
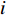
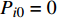
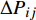
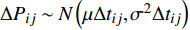
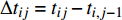
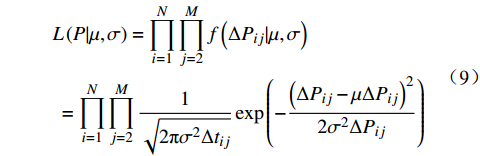
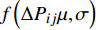
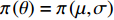
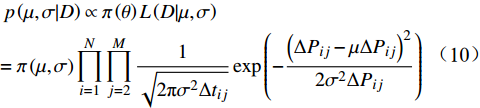
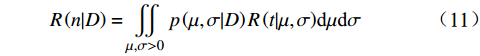
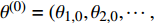
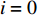
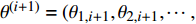
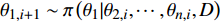
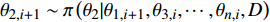
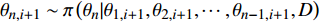
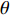
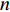
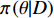

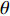
 下载:
下载: