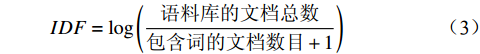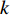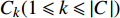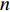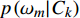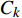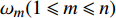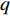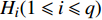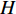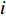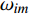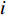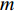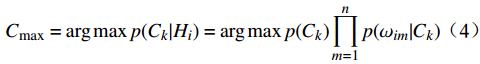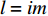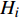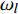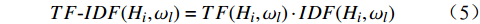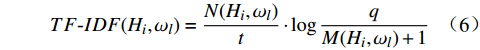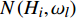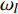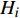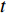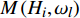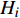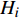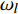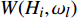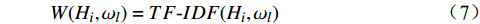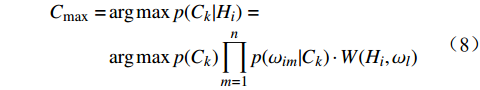列车超速防护（ATP，Automatic Train Protection）系统是保障高速铁路运输安全的关键设备，其安全性和功能性是高速铁路信号系统列车控制的核心。ATP车载设备在研发过程中，要进行大量的仿真测试，须先将测试案例按照测试场景进行分类，便于测试人员编写测试序列，利于后续问题的查找和分析。目前，ATP车载设备测试案例采用人工分类方式，依靠测试人员的经验及对案例的理解，使得案例分类具有较大差异。因此，亟需设计一种方法，实现测试案例自动分类，便于测试的流程化作业。

实现测试案例文本分类的核心，在于对文本特征词的筛选及分类器的选择。在研究分类的过程中，庄媛等人^[1]利用词频—逆文档频率（TF-IDF，Term Frequency-Inverse Document Frequency）算法计算Web服务质量受位置、时间等环境因素影响的权重，结合朴素贝叶斯分类器算法，与基于经典假设检验的SPRT （Sequential Probability Ratio）方法进行对比，实现了Web服务质量的有效监控；周小燕^[2]考虑了特征受到类内和类间分布的影响，引入集中度和分散度，对TF-IDF算法进行优化，结合LDA （Latent Dirichlet Allocation）主题模型得到的主题个数及随机森林函数确定的属性子集，实现用户影评的分类；李新琴等人^[3]采用ADASYN （Adaptive Synthetic Sampling）数据合成法对铁路信号道岔设备故障样本进行处理，选择TF-IDF算法实现特征词提取，集成BiGRU和BiLSTM两个神经网络，得到故障诊断模型，实现信号设备的故障分类；许丽等人^[4]采用向量空间模型对网络热点新闻信息进行处理，利用TF-IDF算法，结合朴素贝叶斯分类器，实现根据提案内容推荐热点信息，但随着测试样本的增多，稳定性和准确性都有所降低；王丽等人^[5]研究了TF-IDF和Word2vec算法提取新闻文本关键词的优缺点，利用KNN （K-Nearest Neighbor）算法，实现新闻数据分类，但不同类别的分类效果差异较大；景丽等人^[6]针对特征词提取不全面等问题，对TF-IDF算法的特征项分布和位置因素进行了优化，结合带有注意力机制的LSTM卷积网络分类模型，实现了更精确的数据分类，但存在时间复杂度较大的问题。

本文针对铁路ATP车载设备测试案例，选择TF-IDF算法对测试案例文本描述进行预处理和特征词提取，依据选取的特征词权重结合朴素贝叶斯算法作为测试案例的分类方法，提高分类效率及准确性。

1   ATP车载设备案例概述

1.1   ATP车载设备

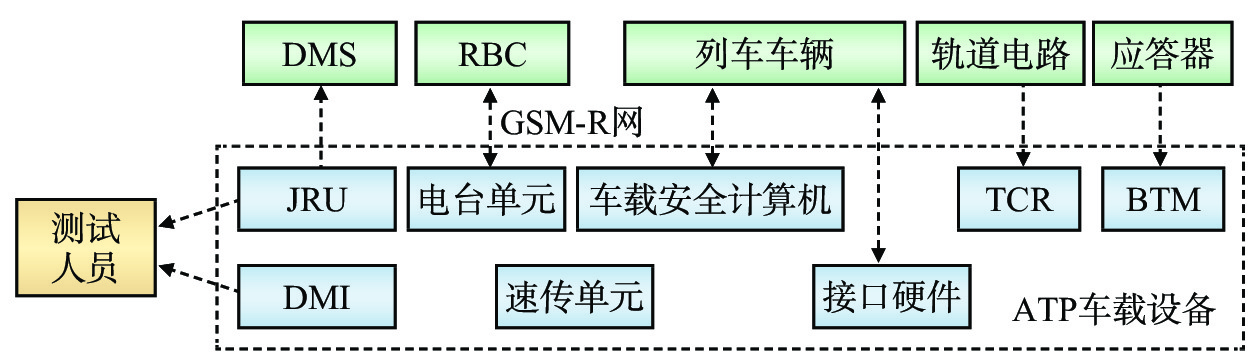
目前，CTCS-3 （Chinese Train Control System Level 3）级列车运行控制（简称：列控）车载系统采用 C2/C3一体化设计，设备的子系统间为分布式结构^[7]。ATP车载设备主要结构如图1所示，包括车载安全计算机、人机交互界面（DMI，Driver Machine Interface）、应答器信息传输模块（BTM，Balise Transmission Module）、司法纪录单元（JRU，Juridical Recording Unit）、轨道电路读取器（TCR，Track Circuit Reader）等，图中箭头表示信息的传递方向。ATP作为CTCS-3级列控系统的车载关键设备及列车自动控制系统的核心^[8]，能够将地面轨道电路、应答器、无线闭塞中心 （RBC，Radio Block Center）等传送来的联锁设备信息、线路信息、距离位置信息等转换为控车数据，生成控车曲线，在列车运行时监控列车运行速度，保障列车的安全间隔，并与车辆系统接口实现信息交互， JRU通过以太网向动态监测系统（DMS，Dynamic Monitoring System） 提供相关车载数据。

图  1  ATP车载设备主要结构

下载: 全尺寸图片 幻灯片

1.2   测试案例概述

ATP车载设备在投入使用前若存在设计问题，极易引发重大事故，造成不可挽回的损失。因此，设备的研发需经历多场景、多轮次的测试，才能保障其安全性，降低在现场使用时发生故障的概率，确保行车安全。车载设备的测试不仅包括各项设计功能实现程度的检测，还包括运用过程中出现故障的分析处理。常规的仿真测试主要分为功能性测试和特殊场景下的故障测试。为保障测试的全面性及系统性，需要测试人员根据系统测试需求，规范编写测试案例。

在遇到系统变更、故障分析等情况时，测试人员可查找现有的测试案例进行验证和分析。ATP车载设备功能复杂，测试案例数目较多，依据ATP的运营场景和功能需求等进行测试案例分类，便于后续分析工作的开展。通常将ATP车载设备CTCS-3级测试案例按照中国国家铁路集团有限公司（简称：国铁集团）发布的《CTCS-3级列控系统测试案例》进行分类，包括制动测试、通信会话管理、控车曲线、应答器链接信息处理、无线消息接收、自动过分相、版本检查、前方轨道空闲（TAF，Track Ahead Free）信息接收和使用、DMI显示、紧急停车消息、故障处理等。

2   基于TF-IDF的特征词提取

2.1   测试案例文本数据

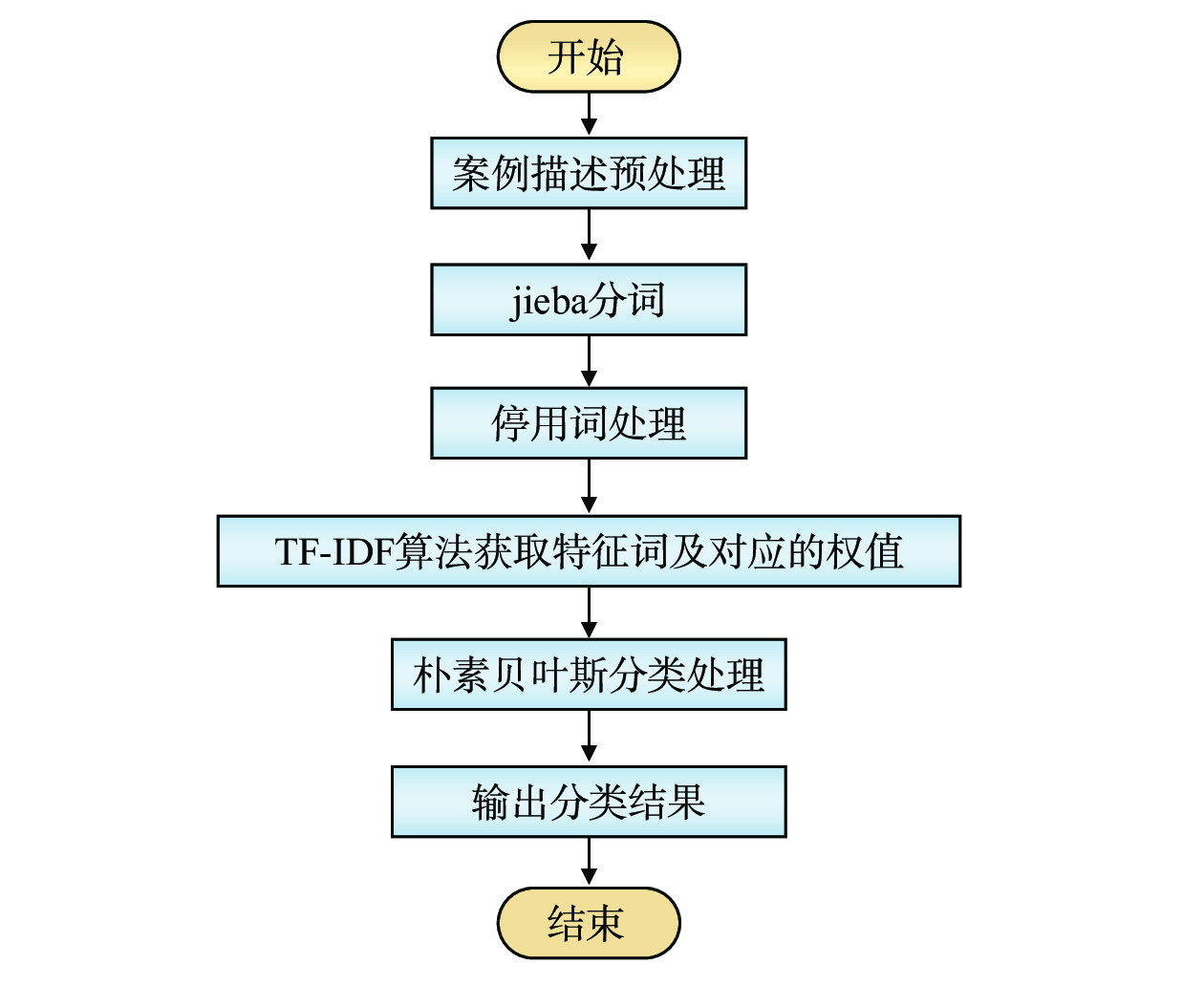
在进行测试案例分类前，需要对案例文本进行分词处理，具体测试案例文本如表1所示。利用Python中现有的jieba分词库对测试案例文本进行分词（分词方法见文献[4]所述）。将文本进行精确分词，便于计算机准确获取文本中的词语。

表  1  测试案例文本示例

案例序号	案例类型	案例描述
1	自检功能	车载上电启动并自检成功（不受地面设备状态影响）后，自动转入待机模式。
2	通信会话管理	由车载发起与最近相关的RBC建立无线通信会话，且系统版本一致。
3	列车数据及配置参数	列车数据二次确认数值未取反
4	应答器链接信息处理	从新数据的起始点（最近相关应答器组）开始，车载使用新的链接信息替代旧的链接信息。
5	制动测试	系统故障模式后下次启动列车，必须进行制动 测试。

下载: 导出CSV 

| 显示表格

2.2   TF-IDF算法

在利用TF-IDF算法获取特征词在全部特征词中的权重值之前，要将利用jieba分词处理后的测试案例语句与停用词库进行比较，过滤无意义的词。去掉停用词后，可在一定程度上降低特征词的维度，增强分类的确定性。

TF-IDF算法是筛选文章特征词的一种方法，该方法可评估前文选取的词在文档中是否具有代表性。如果一个词在本篇文章中出现的频率很高，在其他文章中出现频率相对较低，则该词即为本文的特征词。上述关系可用公式（1）表示^[5]。

其中，TF为进行归一化后的词频，公式为

逆文件频率IDF表示在词频的基础上，赋予每个特征词的权重，公式为

3   TF-IDF加权的朴素贝叶斯算法

3.1   朴素贝叶斯算法

贝叶斯算法适用于目标变量个数较多的情况，是表达不确定问题的有效模型之一。朴素贝叶斯算法在给定属性相互独立的情况下，简化了贝叶斯算法的复杂度^[9]。本文选择该算法实现测试案例的分类，即依据算法得到特征词与预测分类间存在关系概率的大小，选择测试案例适合的分类。

假设文档集$ H $中有$ \left|C\right| $个类别，其中，第$ k $个类别表示为$ {C}_{k}(1\leqslant k\leqslant |C\left|\right) $；$ n $为特征词总数；$ p\left({\omega }_{m}\right|{C}_{k}) $表示在类别$ {C}_{k} $文档中出现特征词$ {\omega }_{m}(1\leqslant m\leqslant n) $的概率；$ q $为文档总数；$ {H}_{i}(1\leqslant i\leqslant q) $表示文档集$ H $中第$ i $个文档；$ {\omega }_{im} $表示第$ i $个文档中第$ m $个特征词；结合文献[10]得到朴素贝叶斯算法分类公式为

3.2   TF-IDF加权的朴素贝叶斯算法

传统的朴素贝叶斯分类方法没有考虑不同类别的特征词权重不同的情况，本文利用TF-IDF算法得到的权重对其改进。

为简化表达式，设变量$ l=im $，对于$ {H}_{i} $中的特征词$ {\omega }_{l} $，其特征权重计算公式为

根据公式（2）和公式（3）可得到

其中，$ N\left({H}_{i},{\omega }_{l}\right) $表示特征词$ {\omega }_{l} $在文档$ {H}_{i} $中出现的次数；$ t $表示全部特征词在文档中出现的次数总和；$ M\left({H}_{i},{\omega }_{l}\right) $是$ {H}_{i} $中含有该特征词的文档数目。因此，文本$ {H}_{i} $中的特征词$ {\omega }_{l} $的特征权重$ W({H}_{i},{\omega }_{l}) $为

将公式（7）引入公式（4）可得到加权的朴素贝叶斯算法分类公式为

将筛选出的特征词及权重带入公式（8），结合已有的训练数据，得到优化后的分类结果。

4   实验与分析

4.1   实验步骤

本实验在Windows操作平台下运行，采用 Python 编程语言编写。本文选取了20个测试案例类型的2001条测试案例，对TF-IDF加权朴素贝叶斯的分类方法进行验证，部分测试案例如表2所示。随机选取1500条案例作为训练数据，501条案例作为验证数据，训练样本与验证样本的比例大致为3∶1。

表  2  案例类型与文本详情节选

序号	案例类别	案例文本详情
1	特定模式信息接收	C2SH模式下拒绝建立无线通信会话的命令。
2	通信会话建立	当安全连接意外中断并且车载未收到结束无线通信会话的命令，则车载认为通信会话仍是建立的，并尝试建立新的 安全连接。
3	列车数据及配置参数	C3OS模式下，车载没有可用的配置参数时使用默认值。
4	应答器链接信息检查	车载对默认报文的处理。
5	列车数据及配置参数	C3OS模式下，仅使用国家值中的目视速度监控列车运行。
6	无线消息接收	未收到RBC对调车请求的应答，车载重复发送调车请求直到指定次数。
7	控车曲线	车载存储的静态速度曲线不能覆盖新接收到的MA的范围，车载拒绝该MA。
8	故障处理	当双系VCU完备状态不一致时，双系VCU检测到双系输入数据以及当前逻辑状态不一致，则使用系统完备状态高的作为主系，将另一系切除。

下载: 导出CSV 

| 显示表格

具体实验参数设置如下：jieba分词处理后文档选定的特征词数量topK=300，返回特征词权重withWeight=True，特征词数目选取max_features=300，测试案例比例test_size=0.25。

本文利用jieba分词得到的训练词库示例如图2所示，利用TF-IDF算法得到的特征词及其对应的权值示例如图3所示，选取权值较大的前300个词进行贝叶斯分类，得到测试案例的分类结果，测试案例分类流程如图4所示。

图  2  利用jieba分词得到的训练词库示例

下载: 全尺寸图片 幻灯片

图  3  利用TF-IDF算法得到的特征词及其对应权值示例

下载: 全尺寸图片 幻灯片

图  4  测试案例分类流程

下载: 全尺寸图片 幻灯片

4.2   实验结果分析

4.2.1   分类结果分析

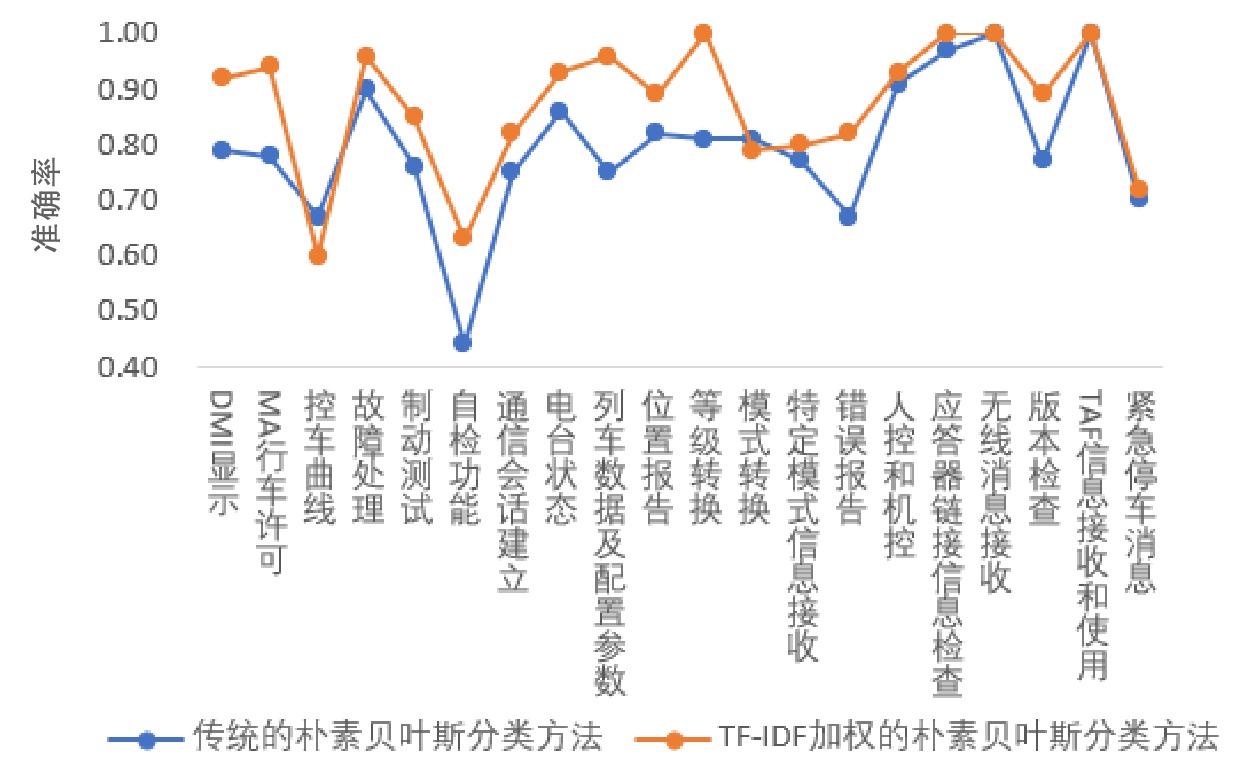
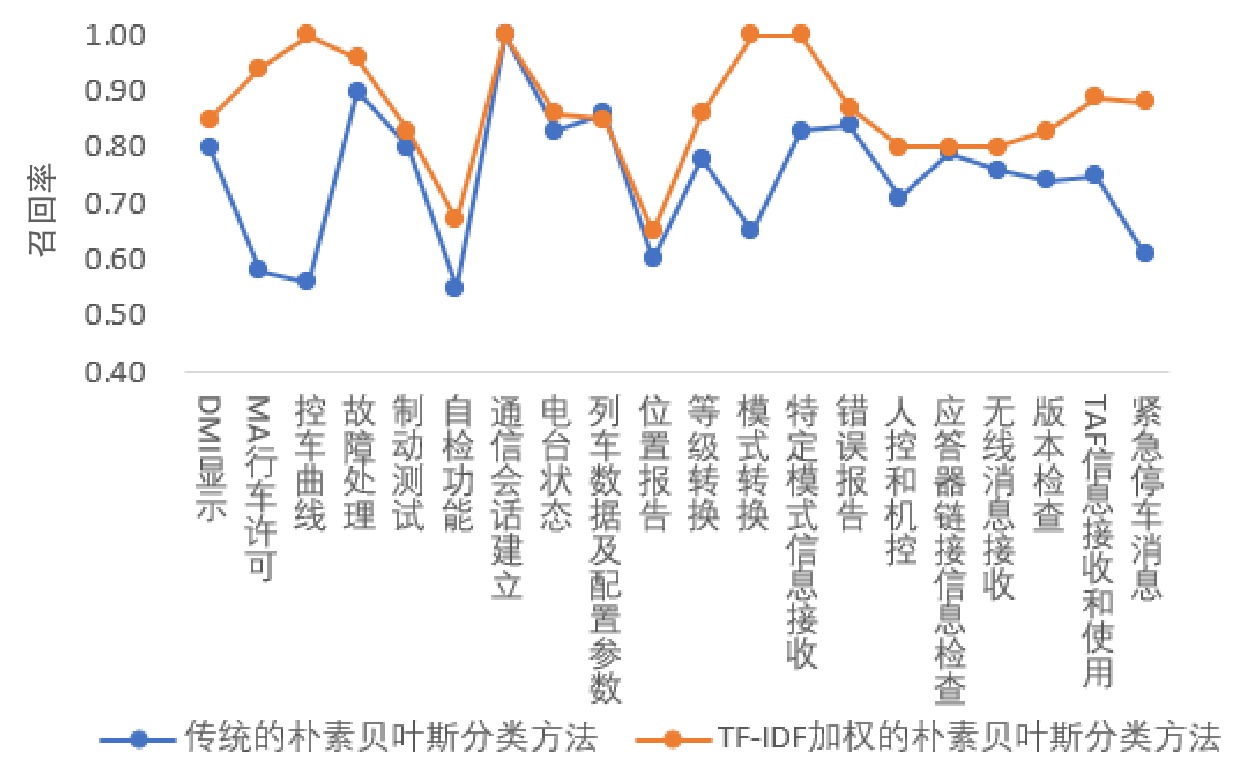
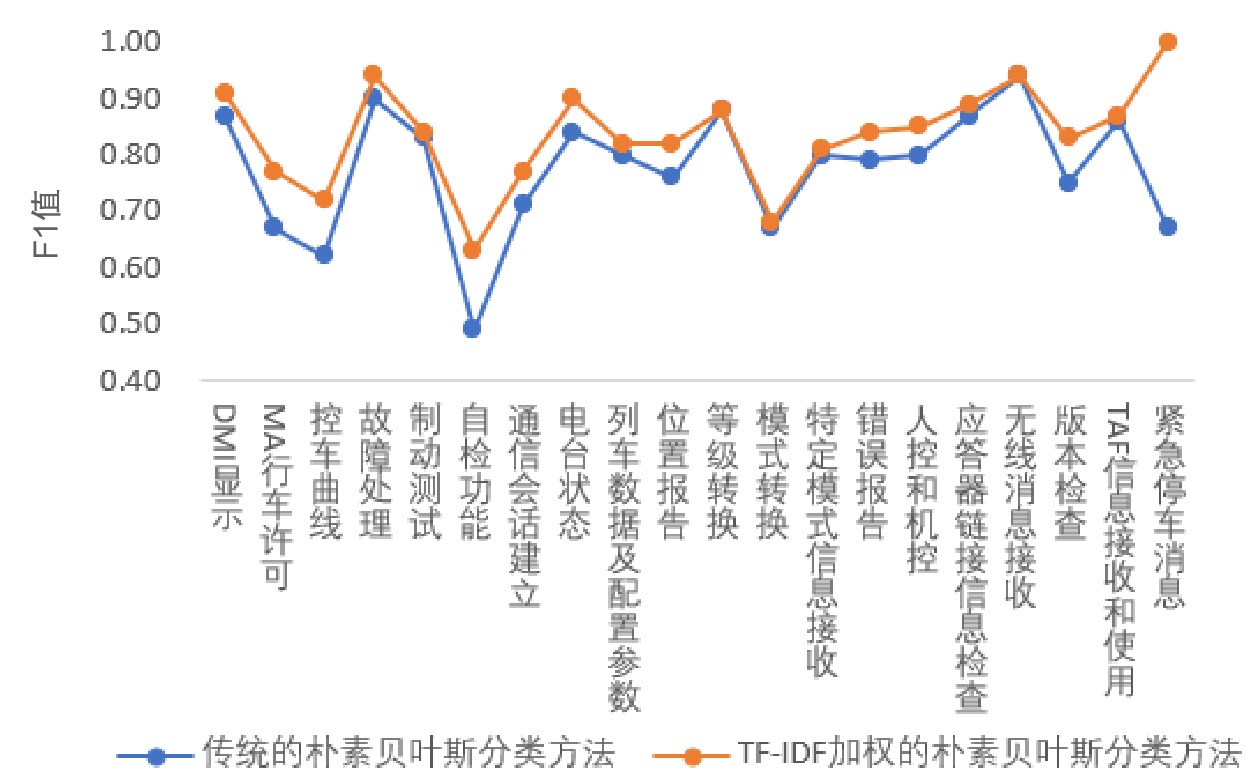
本文采用文献[11]提到的准确率、召回率及F1值作为判断分类有效性的指标。利用传统朴素贝叶斯分类方法和TF-TDF加权的朴素贝叶斯分类方法实现测试分类，其各自结果对应的指标变化如图5、图6、图7所示。

图  5  准确率指标变化情况

下载: 全尺寸图片 幻灯片

图  6  召回率指标变化情况

下载: 全尺寸图片 幻灯片

图  7  F1值变化情况

下载: 全尺寸图片 幻灯片

从图5、图6、图7可看出，相比于传统算法，利用加权后的朴素贝叶斯算法得到的分类效果较好，对应的评价指标总体水平呈现提升的趋势。如果用人工方式实现上述测试案例的分类，需要近3天的时间，利用本算法仅需几秒，从工作时间的对比可看出本算法显著提高了工作效率。

4.2.2   分类指标对比

依据文献[12]提及的准确度、宏平均及加权平均指标，结合表3得到的结果可发现，在测试案例数目相同的情况下，利用TF-IDF加权的朴素贝叶斯算法的加权平均值与传统的朴素贝叶斯算法的加权平均值相比，准确率指标有6%的提升，召回率指标有2%的提升，F1值有3%的提升。实验证明了基于TF-IDF加权的朴素贝叶斯算法分类的有效性与准确性。

表  3  分类报告对比

算法	评价指标	准确率	召回率	F1值
TF-IDF加权的 朴素贝叶斯算法	准确度			0.84
	宏平均	0.81	0.85	0.82
	加权平均	0.88	0.84	0.84
朴素贝叶斯算法	准确度			0.79
	宏平均	0.75	0.72	0.72
	加权平均	0.82	0.79	0.80

下载: 导出CSV 

| 显示表格

5   结束语

本文以实验室现有列控车载设备CTCS-3实际生产数据为测试案例，选择了基于文本挖掘的测试案例分类方法，利用TF-IDF算法实现了高速铁路列控车载设备CTCS-3级案例中的特征词及对应权重的筛选，将得到的权重结合朴素贝叶斯算法实现了测试案例自动分类，相比于传统的人工分类法显著提高了分类效率及准确性。

实验结果表明，本文方法可为高速铁路ATP车载设备测试人员分类测试案例提供有力支撑，具有很强的实用性。后续将针对朴素贝叶斯分类器性能受属性关系影响的问题开展进一步的研究。