高级检索 加入收藏
  • 查询稿件
  • 获取最新论文
  • 知晓行业信息
官方微信 欢迎关注

BDS-3精密单点定位在铁路勘测中的应用研究

朱昀, 冯威, 王国祥, 郑子天, 潘佩芬

朱昀, 冯威, 王国祥, 郑子天, 潘佩芬. BDS-3精密单点定位在铁路勘测中的应用研究[J]. 铁路计算机应用, 2022, 31(9): 14-19. DOI: 10.3969/j.issn.1005-8451.2022.09.03
引用本文: 朱昀, 冯威, 王国祥, 郑子天, 潘佩芬. BDS-3精密单点定位在铁路勘测中的应用研究[J]. 铁路计算机应用, 2022, 31(9): 14-19. DOI: 10.3969/j.issn.1005-8451.2022.09.03
shu
ZHU Yun, FENG Wei, WANG Guoxiang, ZHENG Zitian, PAN Peifen. BDS-3 precise point positioning applied to railway survey[J]. Railway Computer Application, 2022, 31(9): 14-19. DOI: 10.3969/j.issn.1005-8451.2022.09.03
Citation: ZHU Yun, FENG Wei, WANG Guoxiang, ZHENG Zitian, PAN Peifen. BDS-3 precise point positioning applied to railway survey[J]. Railway Computer Application, 2022, 31(9): 14-19. DOI: 10.3969/j.issn.1005-8451.2022.09.03
shu

BDS-3精密单点定位在铁路勘测中的应用研究

  • 1.

    西南交通大学　地球科学与环境工程学院，成都　611756

  • 2.

    中铁二院工程集团有限责任公司　测绘工程设计研究院，成都　610031

  • 3.

    中国铁道科学研究院集团有限公司　电子计算技术研究所，北京　100081

基金项目: 中国国家铁路集团有限公司科技研究开发计划重大课题（K2020X017）
详细信息
    作者简介:

    朱　昀，在读硕士研究生

    王国祥，高级工程师

  • 中图分类号:  U212.2 : P228.4 : TP39

BDS-3 precise point positioning applied to railway survey

  • 1.

    Faculty of Geosciences and Environmental Engineering, Southwest Jiaotong University, Chengdu　 611756, China

  • 2.

    Institute of Surveying and Mapping Engineering Design and Research, China Railway Eryuan Engineering Group Co. Ltd., Chengdu　610031, China

  • 3.

    Institute of Computing Technologies, China Academy of Railway Sciences, Beijing　100081, China

摘要

    摘要
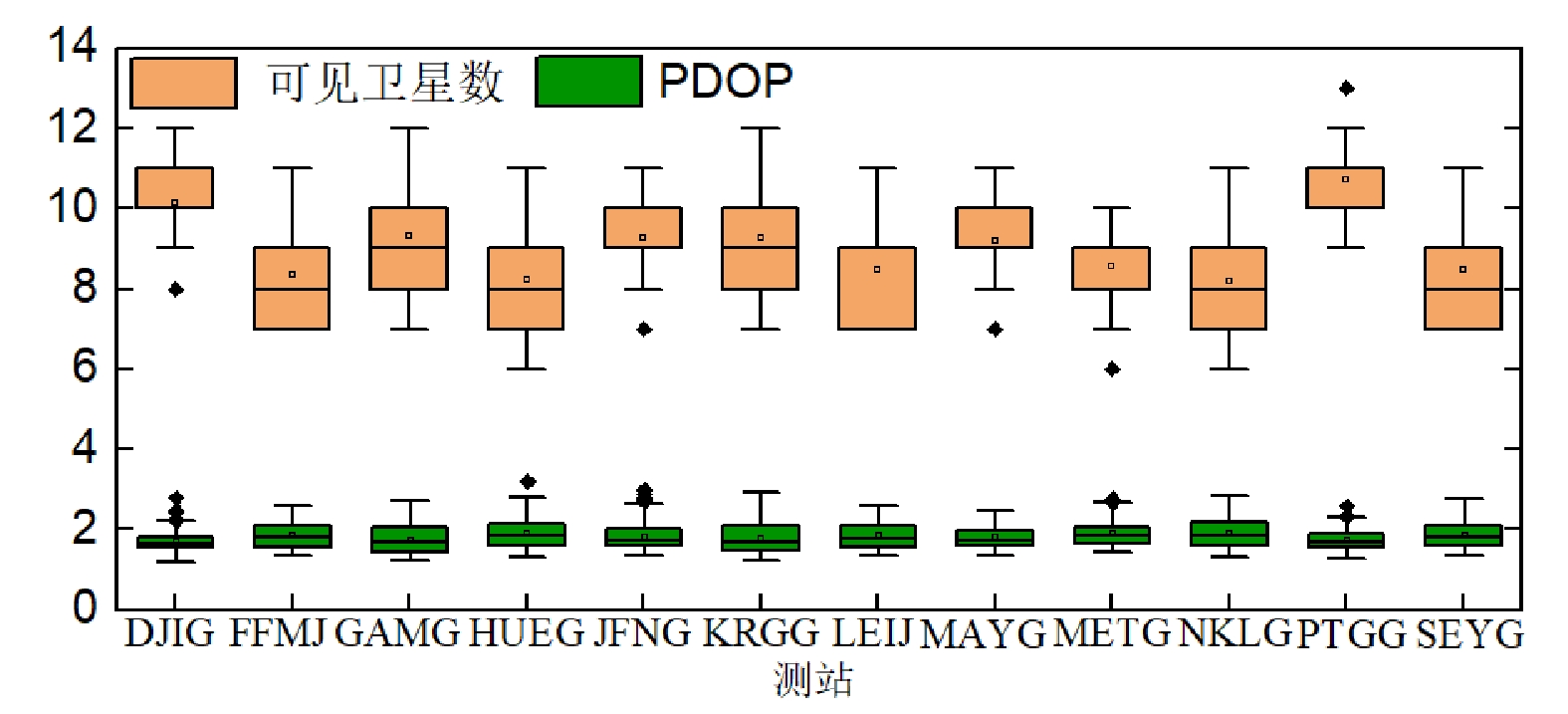
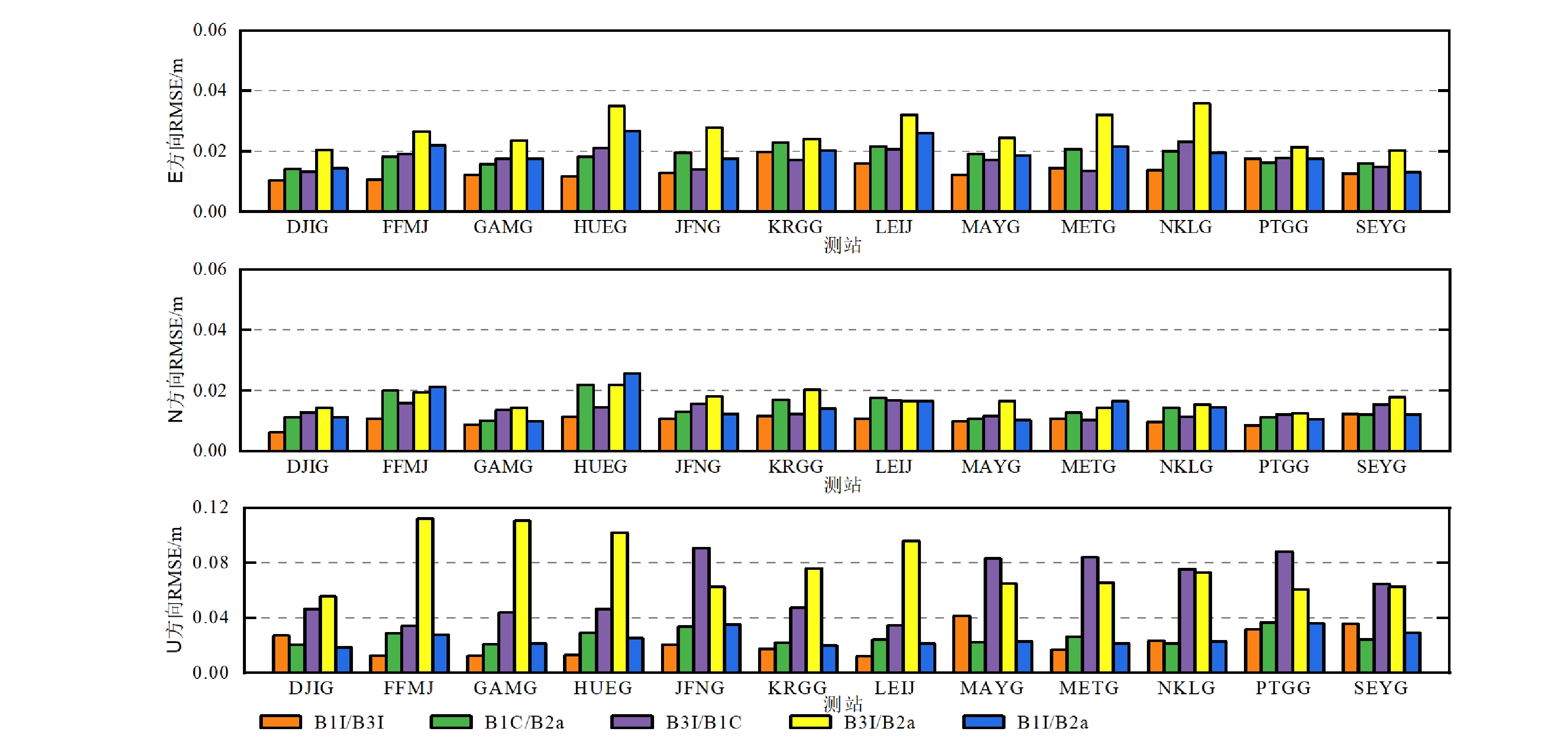
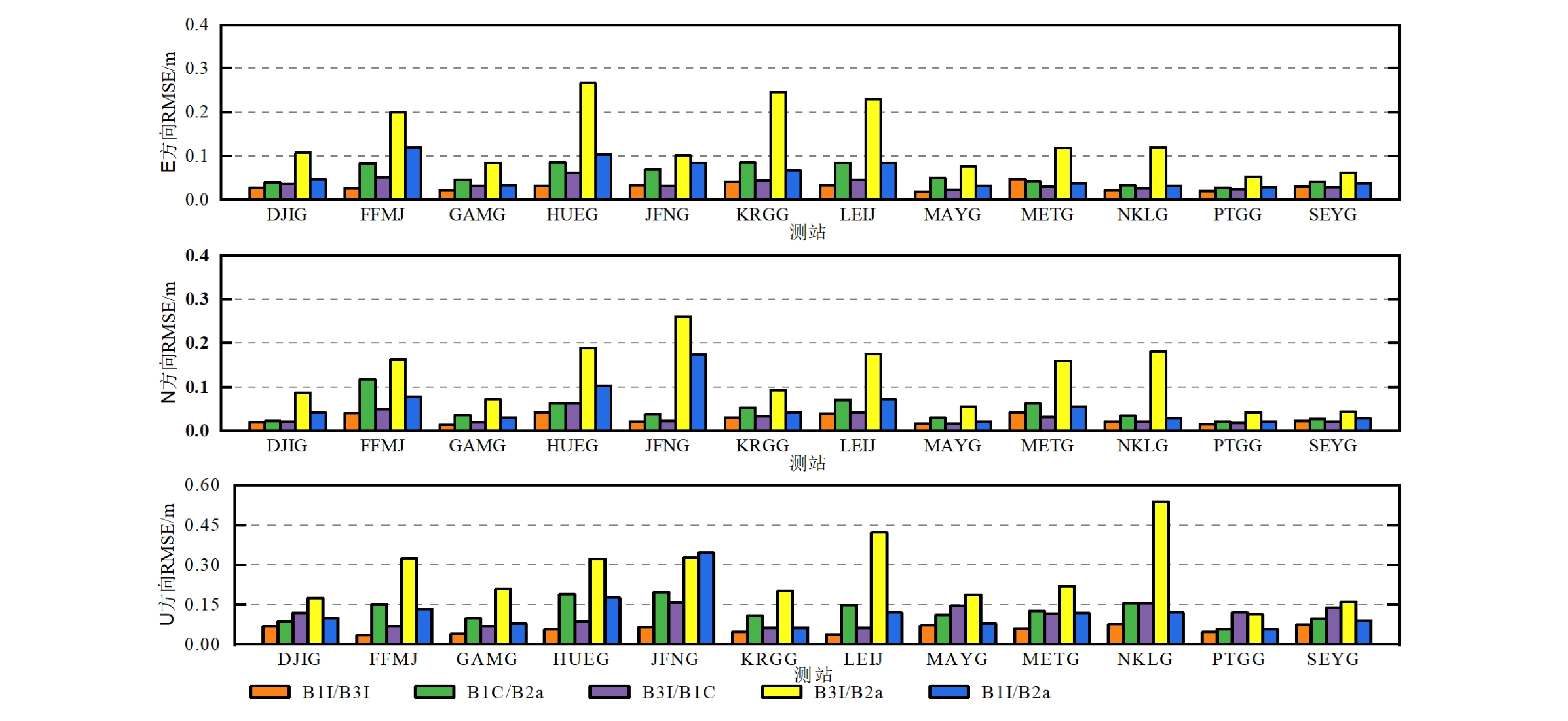
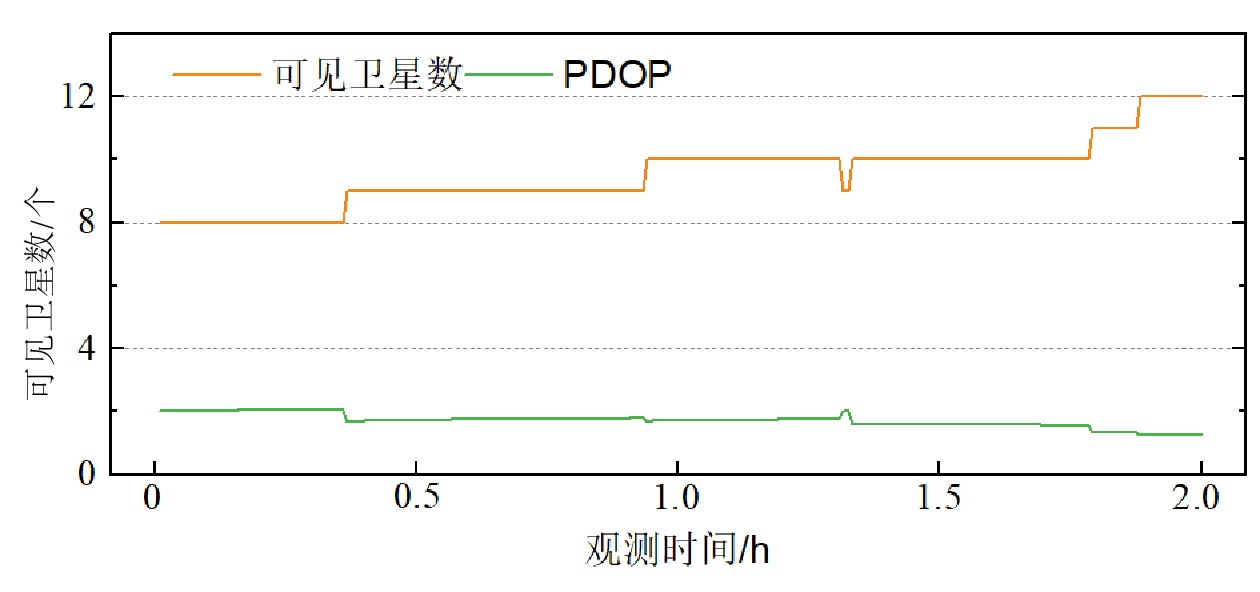
  • 摘要: 为研究第三代北斗卫星导航系统（BDS -3，BeiDou Navigation Satellite System-3 ）精密单点定位技术（PPP ，Precise Point Positioning）在铁路勘测应用中的可行性，文章推导了BDS-3任意双频非差非组合PPP通用函数模型，并采用该模型对BDS-3卫星B1I、B3I、B1C和B2a信号形成的5种双频组合进行PPP解算和性能分析，利用某铁路观测数据，对BDS-3进行PPP解算。结果表明， 所有观测时段内可见卫星数约为7～11颗，空间位置精度因子（PDOP，Position Dilution of Precision）值约为2.0，可见卫星数较多，且空间几何分布良好；在静态和仿动态解算模式下，在水平和高程方向均可实现厘米级的定位精度。该研究可为BDS-3精密单点定位技术在铁路勘察中的应用提供参考。
    Abstract: In order to study the feasibility of BeiDou Navigation Satellite System (BDS)-3 Precise Point Positioning (PPP) in railway survey application, this paper used BDS-3 satellite observation data to deduce BDS-3 arbitrary dual-frequency undifferenced and uncombined PPP universal function model. By using this model, the paper carried out the PPP solutions and performance analysis of five dual-frequency combinations formed by BDS-3 satellite signals B1I, B3I, B1C and B2a, and used a railway observation data to calculate BDS-3 PPP. The results show that the number of visible satellites is about 7~11, and the spatial Position Dilution of Precision (PDOP) is about 2.0 during the observation period. The number of visible satellites is large and the spatial geometry distribution is good. BDS-3 can achieve centimeter-level positioning accuracy in both horizontal and elevation directions in static and pseudo-dynamic solution modes. This study can provide reference for the application of BDS-3 precision point positioning technology in railway survey.
    • HTML全文

  • 图  1   12个测站可见卫星数和PDOP值分布

    下载: 全尺寸图片 幻灯片

    图  2   5种双频组合下12个测站单天静态解平均RMSE

    下载: 全尺寸图片 幻灯片

    图  3   5种双频组合下12个测站动态解平均RMSE

    下载: 全尺寸图片 幻灯片

    图  4   控制点卫星可见数与PDOP值

    下载: 全尺寸图片 幻灯片

    图  5   控制点静态（左）和仿动态（右）定位偏差序列及不同观测时长定位精度

    下载: 全尺寸图片 幻灯片

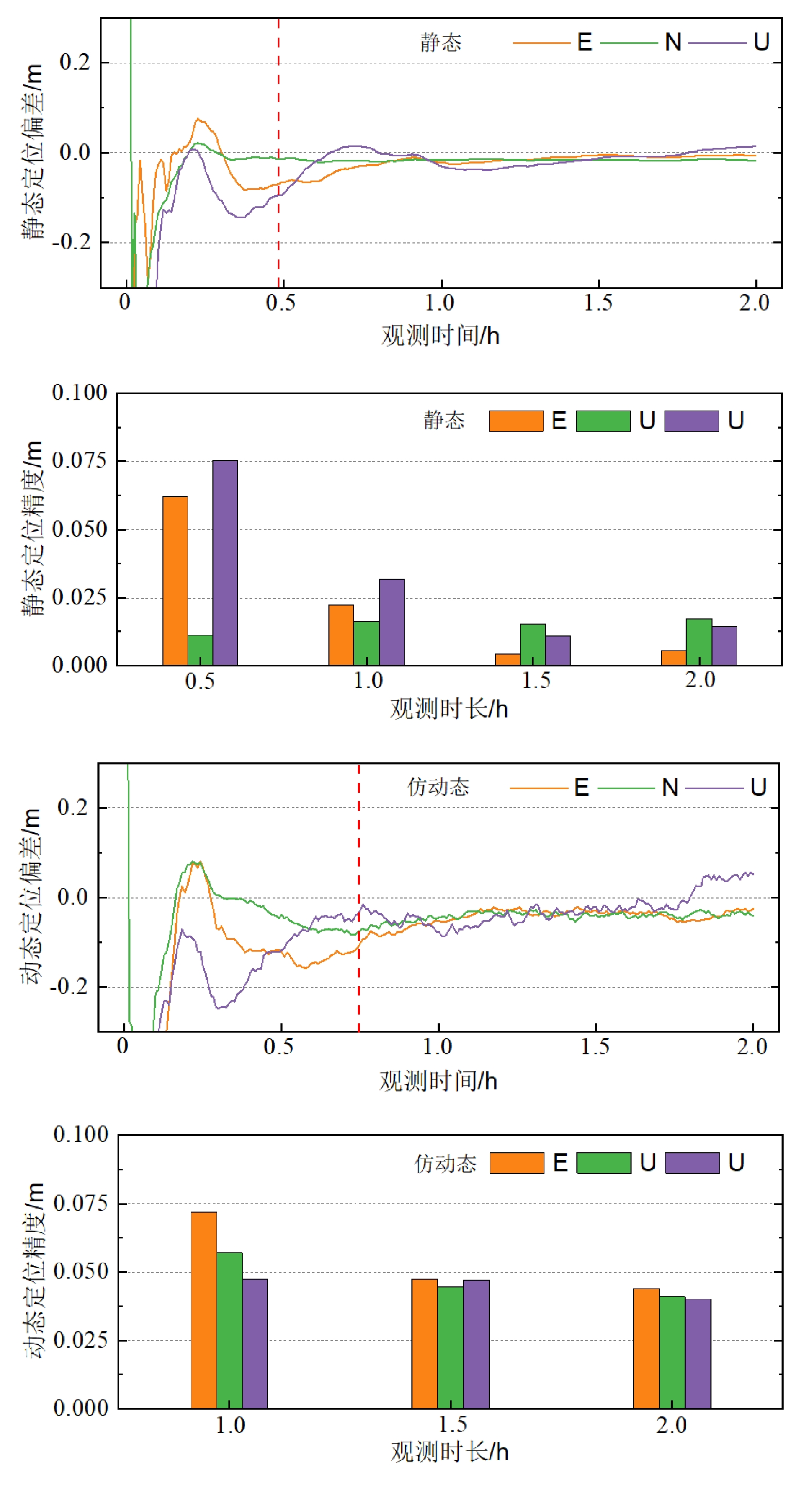
    表  1   5种双频组合12个测站静态解平均RMSE和收敛时间

    组合频点定位精度RMSE/cm收敛时间/min
    ENU
    B1I/B3I1.41.02.237
    B1C/B2a1.91.42.6103
    B3I/B1C1.71.46.272
    B3I/B2a2.71.78.0205
    B1I/B2a2.01.52.587
    下载: 导出CSV

    表  2   5种双频组合12个测站动态解平均RMSE和收敛时间

    组合频点定位精度RMSE/cm收敛时间/min
    ENU
    B1I/B3I3.02.75.749
    B1C/B2a5.74.812.8182
    B3I/B1C3.73.010.9126
    B3I/B2a18.915.632.6332
    B1I/B2a5.85.612.1194
    下载: 导出CSV
    • 参考文献(11)
  • [1] 李　杨, 高淑照, 惠晨亮, 等. BDS在铁路工程测量应用中的精度分析[J/OL]. 导航定位学报, 2022(04): 1-10[2022-02-24]. http://kns.cnki.net/kcms/detail/10.1096.P.20211207.1950.002.html.
    [2] 陶　灿, 曹成度, 滕焕乐, 等. 基于单一北斗二代系统的高速铁路CP0框架控制网基线解算和精度分析[J/OL]. 铁道标准设计: 1-7[2022-02-24]. https://doi.org/10.13238/j.issn.1004-2954.202009150007.
    [3] 靳成铭,蔡伯根,王 剑,等. 铁路导航精密单点定位方法改进及性能验证 [J]. 铁道学报,2020,42(12):82-89. DOI: 10.3969/j.issn.1001-8360.2020.12.011
    [4] 张小红,胡家欢,任晓东. PPP/PPP-RTK新进展与北斗/GNSS PPP定位性能比较 [J]. 测绘学报,2020,49(9):1084-1100. DOI: 10.11947/j.AGCS.2020.20200328
    [5] 梅建东. GPS双频/三频静态精密单点定位精度分析 [J]. 测绘标准化,2021,37(3):37-41.
    [6] 郭树人,蔡洪亮,孟轶男,等. 北斗三号导航定位技术体制与服务性能 [J]. 测绘学报,2019,48(7):810-821.
    [7]

    Zhang Rui, Tu Rui, Zhang Pengfei, et al. Orbit determination of BDS-3 satellite based on regional ground tracking station and inter-satellite link observations [J]. Advances in Space Research, 2021, 67(12): 4011-4024. DOI: 10.1016/j.asr.2021.02.027
    [8] 刘生锋,杨文龙,谷 涛. BDS-3双频组合精密单点定位精度分析 [J]. 测绘通报,2021(3):7-11,17.
    [9] 陈哲正,欧阳明俊,朱祥维,等. 北斗三号精密单点定位精度分析研究 [J]. 全球定位系统,2021,46(2):37-43. DOI: 10.12265/j.gnss.2020112701
    [10] 周　锋. 多系统GNSS非差非组合精密单点定位相关理论和方法研究[D]. 上海: 华东师范大学, 2018.
    [11] 赵 琳,李宏宇,侯毅男,等. 多系统混频非差非组合精密单点定位方法研究 [J]. 导航定位与授时,2021,8(5):96-102.
    • 相关文章
    • 施引文献(6)

  • 期刊类型引用(1)

    1. 谭飞刚，余志立，刘开元，李汀. 车载单目摄像机下地铁轨行区检测与提取. 铁道标准设计. 2022(09): 74-77 . 百度学术

    其他类型引用(5)

    • 资源附件(0)
图(5)  /  表(2)
计量
  • 文章访问数:  83
  • HTML全文浏览量:  27
  • PDF下载量:  13
  • 被引次数: 6
出版历程
  • 收稿日期:  2022-02-28
  • 刊出日期:  2022-09-28

目录

摘要
HTML全文
    参考文献(11)
    相关文章
    施引文献(6)
    资源附件(0)

    /

    返回文章
    返回

    京ICP备12043220号-2

    本系统版权所有：北京仁和汇智信息技术有限公司   百度统计