Segmented fitting method of line features of digital track map
-
摘要: 基于全球卫星导航系统（GNSS ，Global Navigation Satellite System）的列车定位技术降低了铁路建设与运营的成本，数字轨道地图作为地图匹配方法的基础，通常作为辅助定位手段对卫星定位偏差进行校正，对轨道线形进行准确描述及约简是轨道电子地图构建存储的前提。文章采用方位角近似估计曲率的方法对轨迹平面线形进行初步识别分类，为提高线形的拟合精度，引入自适应权值因子，对最小二乘拟合法进行优化，以消除大偏差观测数据对拟合趋势的影响，从而保证整体轨迹数据的平滑拟合及精度。实测车辆轨迹数据验证表明，该算法可对车辆轨迹线路特征进行有效提取及准确描述。
-
关键词:
- 全球卫星导航系统（GNSS） /
- 数字轨道地图 /
- 平面线形 /
- 分段曲线拟合 /
- 方位角
Abstract: The train positioning technology based on the Global Navigation Satellite System (GNSS) reduces the cost of railway construction and operation. As the basis of map matching method, digital orbit map is usually used as an auxiliary positioning means to correct satellite positioning deviation. Accurate description and reduction of track alignment are the premise of the construction and storage of track electronic map. This paper used the azimuth approximate estimation of curvature to preliminarily identify and classify the track plane alignment. In order to improve the fitting accuracy of the line shape, the paper introduced an adaptive weight factor to optimize the least squares fitting method, and eliminate the influence of large deviation observation data, thereby ensure the smooth fitting and accuracy of the overall trajectory data. The verification of measured vehicle trajectory data shows that the algorithm can effectively extract and accurately describe the characteristics of vehicle trajectory. -
由我国北斗卫星导航、欧洲Galileo、美国全球定位系统（GPS，Global Positioning System）、俄罗斯全球导航卫星系统（GLONASS，Global Navigation Satellite System）组成的全球导航卫星系统（GNSS ，Global Navigation Satellite System）在铁路交通领域得到了广泛的应用。基于GNSS的列车定位系统定位方式不同于传统轨道电路及应答器辅助的定位方式，减少了轨旁设备的铺设，降低了建设和运营成本，提高了铁路运输的效率。基于卫星的列车定位方式作为铁路关键安全应用中的一部分，其对可靠性与安全性要求更高[1]。
考虑到铁路轨道可将列车约束至既定线路，许多学者将地图匹配技术作为定位辅助手段，以校正GNSS定位误差，这种方式很大程度上提高了列车定位的精度，同时也节约了成本。而作为地图匹配方法实现的前提，轨道电子地图对线路地理和几何信息的准确描述直接影响了地图匹配算法的精度，因此，构建高精度的轨道电子地图是非常必要的[2]。在地理信息系统中常通过多条折线逼近的方式来描述曲线段，虽然有效，但会使线路的整体特征无法体现，同时损失了轨迹数据的精度[3]，不适用于铁路列车定位领域。
许多学者就轨道电子地图的构建方法进行了研究，文献[4—5]通过卡尔曼 (Kalman) 滤波算法构建预测方程，对采集到的数据集进行野值数据的剔除，利用角度差法对处理后的轨迹数据进行分段曲线拟合，完成轨道电子地图的构建；文献[6]针对原始GPS地图测量数据，采用多点加权距离检验及Kalman估计差值检验实现错误数据剔除，利用三次B样条曲线反算生成拟合曲线，并按照一定的距离分辨率进行等距离插值，实现轨道电子地图的构建；文献[7]利用启发式算法对轨迹数据进行约简，通过分段折线对轨道线形进行描述；文献[8—9]研究从大量低精度的GPS轨迹数据融合生成高精度GPS数据的快速算法，通过对比得出最优的轨迹融合表示结果；文献[10]针对线形的识别进行研究，采用启发式算法对直线、圆曲线和缓和曲线段进行识别拟合，但需要选定初始点，且算法复杂；文献[11]提出了一种低成本的水平对齐拟合方法，通过曲率和方向讨论了点位置误差对道路线形表示噪声的影响，但拟合精度不高；文献[12]通过计算方位角近似估计曲率的方式对线形进行初步识别，通过设定横向误差对直线段和圆曲线段进行迭代，直至特征点确定，并采用最小二乘（LS，Least Squares）方法进行拟合，完成线路描述，但没有考虑到野值对拟合精度的影响。
本文考虑野值数据的影响，采用方位角近似估计曲率的方式对轨迹平面线形进行初步识别分类，设定横向误差为约束条件，对直线及曲线的分界点进行确定，采用引入自适应权值因子的LS方法进行分段轨迹的拟合，以提高可靠轨迹数据拟合权值，而降低野值数据拟合权值的思路提高轨迹拟合平滑度，完成整体的线路地图构建。
1 铁路平面线形识别
1.1 铁路平面线形介绍
通常，实际铁路线路在设计的过程中受地形、技术等因素的限制，不能以单一长直线进行铁轨的铺设，为提高行车安全及舒适度，在列车转向处往往需要将相邻的两段直线用平面曲线连接起来，以减少对行驶列车的冲击。铁路线路通常划分为直线、圆曲线、缓和曲线3种类型，其中，缓和曲线分为前缓和曲线与后缓和曲线，主要实现直线与圆曲线之间的过渡，铁路的线形平面示意如图1所示。
半径、方位角及曲率作为铁路平面线形的3个描述指标，其特点如表1所示，表中，R为圆曲线半径。
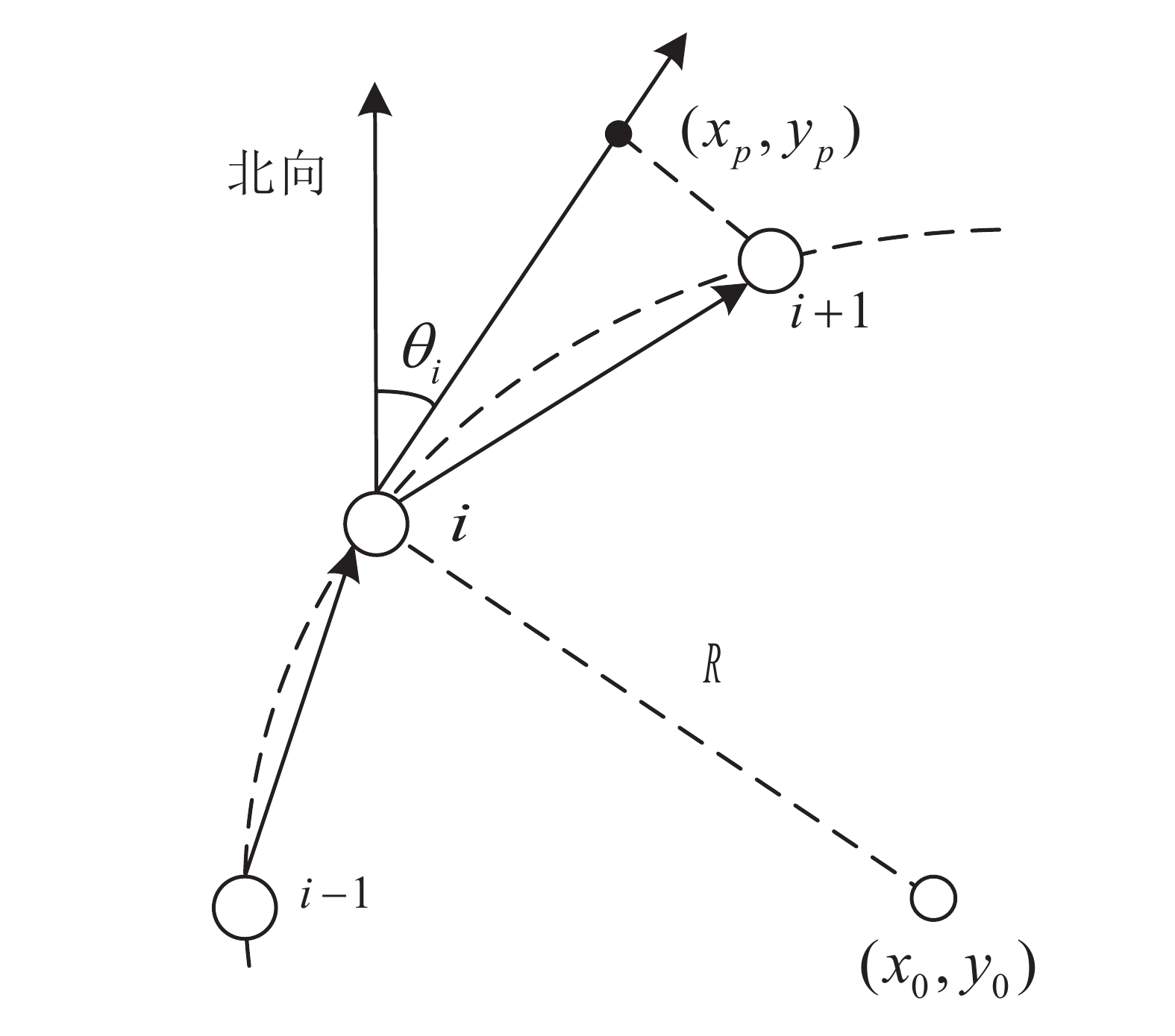
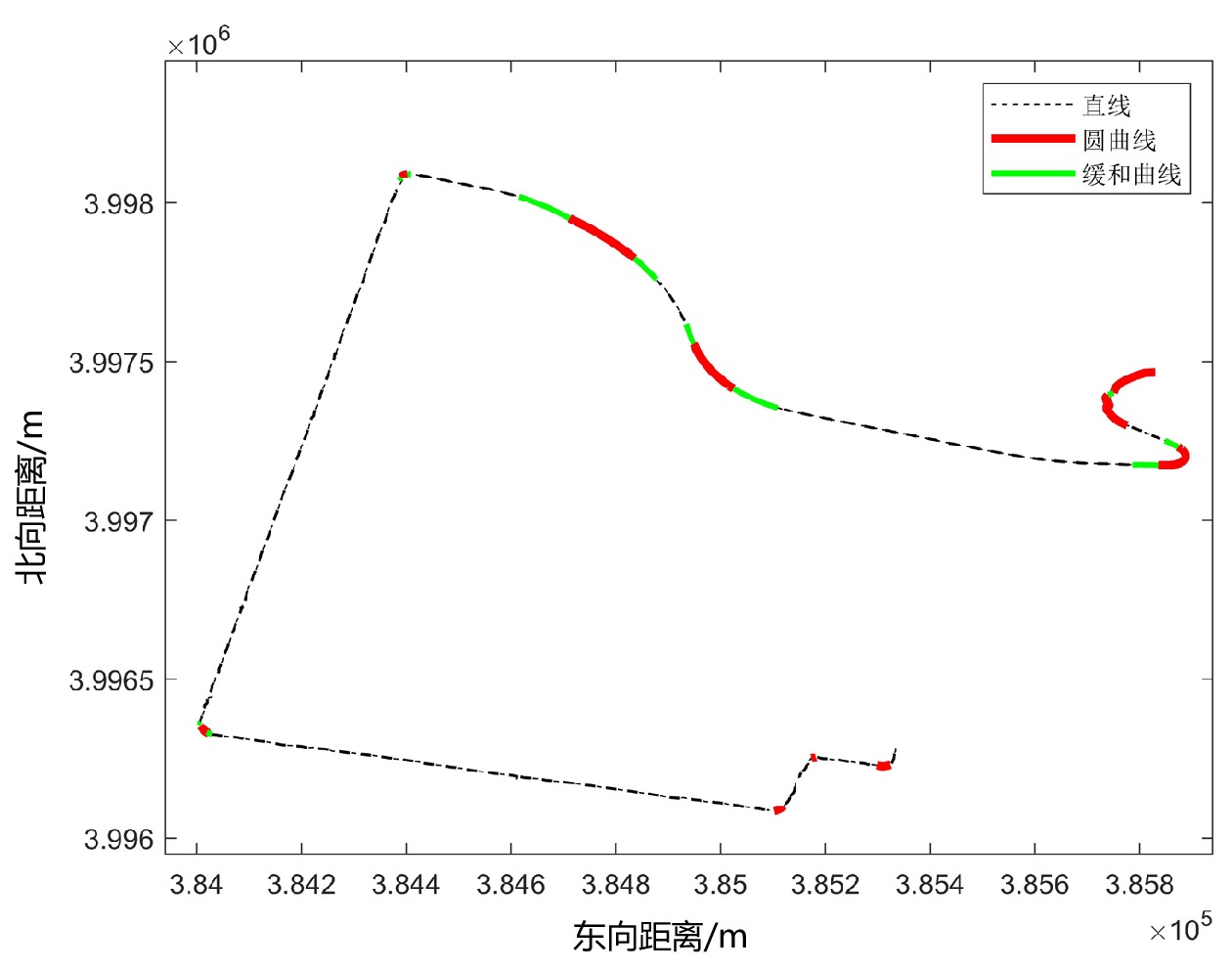
表 1 铁路线形平面参数特点平面线形 直线 缓和曲线 圆曲线 半径 / $ R \to \infty $ $ R $ 方位角 定值 二次抛物线变化 线性递增/递减 曲率 恒为0 线性变化 $ 1/R $ 1.2 基于方位角曲率特征的平面线形识别
铁路线路中心各轨迹点的方位角是指从该观测点正北方向起，绕顺时针方向至该观测点方向线之间所成的水平夹角。参照文献[12]，利用圆弧切线法计算各轨迹点的方位角，如图2所示，采用“三点定圆法”计算圆心
$ ({x_0},{y_0}) $ 和半径$ R $ ，将观测点在圆弧的切线与正北方向的夹角作为该点的方位角，方位角表达式为$$ {\theta _i} = \arctan \frac{{{x_p} - {x_i}}}{{{y_p} - {y_i}}} $$ (1) 其中，
$ {\theta _i} $ 为当前观测点的方位角，且$ {\theta _i} \in [{0^ \circ },{360^ \circ }] $ ；$ ({x_i},{y_i}) $ 为当前点$ i $ 的坐标；$ ({x_p},{y_p}) $ 为后一点$ i + 1 $ 在圆弧切线方向的投影坐标。则当前点的近似曲率为$$ {\rho }_{i}=\frac{{\theta }_{i+1}-{\theta }_{i}}{dis(i,i+1）} $$ (2) 其中，
$ {\rho _i} $ 为当前点$ i $ 的近似曲率；$ dis(i,i + 1) $ 为前后两点坐标的投影距离。依据平面线形的曲率特点，设定曲率阈值，对直线线形及曲线线形进行划分。将横向误差作为约束条件对圆曲线及缓和曲线进行划分，横向误差通常取0.25 m。
平面线形识别算法流程如图3所示。（1）通过所测GNSS轨迹点坐标计算方位角，由方位角计算出该点斜率；（2）出于测量误差会影响计算的考虑，使用滑动平均法对采集轨迹点的方位角和曲率进行平滑滤波；（3）利用直线路段曲率为零的特点，对轨迹进行直线段及曲线路段的初步划分；（4）设定横向测量误差为约束条件，对识别出的路段依据对应模型进行迭代拟合，从而确定出3种线形的起始点、终止点及相关描述参数，得到轨迹的整体平面线形表示。
2 铁路平面线形拟合
2.1 最小二乘平面线形拟合方法
对轨迹点所处平面线形进行确定之后，需根据不同线形的特点选取对应的数学模型进行轨迹点的初步拟合，并求解不同线形模型的相关参数。本文使用常见的曲线拟合法—LS方法[13]对轨迹点进行拟合。将轨迹点坐标作为观测量，线形模型参数为待估计量，即根据一系列离散点
$ ({x_i},{y_i}) $ ，求近似曲线函数$ y = C(x) $ ，将轨迹点到曲线拟合点的残差平方和最小的函数作为LS拟合曲线函数。LS形拟合算法的主要步骤如下。Step1：根据给定的
$ m $ 个观测轨迹点数据$({x}_{i},{y}_{i})$ (i=1,2,···, m )，确定多项式曲线为$$ C(x) = \sum\limits_{j = 0}^n {{a_i}{x^i}} = {a_0} + {a_1}x + {a_2}{x^2} + ... + {a_n}{x^n} $$ (3) 其中，
${a_j}(j = 0,1,2, \cdots ,n)$ 为多项式各项的待定系数。将式（3）用矩阵形式表示为
$$ C(x) = {\boldsymbol{A}}{X_0} $$ (4) 其中，
${\boldsymbol{A}} = \left[ {{a_0},{a_1},{a_2},\cdots,{a_n}} \right]$ 为多项式的各项待定系数矩阵。Step2：记点
$ ({x_i},{y_i}) $ 到拟合曲线$ y = C(x) $ 残差为$ {\delta _i} $ ，故曲线拟合残差的平方和$ \left\| \delta \right\|_2^2 $ 为$$ \left\| \delta \right\|_2^2 = \sum\limits_{i = 0}^m {{{\left[ {\sum\limits_{j = 0}^n {{a_j}{x^j}} - {y_i}} \right]}^2}} $$ (5) 若要使其残差平方和最小，则曲线拟合的目标函数为
$$ \left\{ \begin{gathered} \begin{array}{*{20}{c}} {\min }&{\left\| \delta \right\|_2^2} \end{array} \\ \left\| \delta \right\|_2^2 = \sum\limits_{i = 0}^m {\delta _i^2} = \sum\limits_{i = 0}^m {{{\left[ {C({x_i}) - {y_i}} \right]}^2}} \\ \end{gathered} \right. $$ (6) Step3：将曲线拟合问题转化为求解目标函数极小值点，则根据
$ \dfrac{{\partial \left\| \delta \right\|_2^2}}{{\partial {a_k}}} = 0 $ 可得$$ 0 = \frac{{\partial \left\| \delta \right\|_2^2}}{{\partial {a_k}}} = 2\sum\limits_{i = 0}^m {\left[ {\sum\limits_{j = 0}^n {{a_j}{x^j}} - {y_i}} \right]} {x^k} $$ (7) k = 0,1,···,n ，整理可得
$$ \sum\limits_{i = 0}^m {\sum\limits_{j = 0}^n {{a_j}{x^{j + k}}} = \sum\limits_{i = 0}^m {{x^k}{y_i}} }$$ (8) Step4：利用矩阵形式表示为
${\boldsymbol{X}}{{\boldsymbol{A}}^T} = {\boldsymbol{Y}}$ ，则可知$$ {\boldsymbol{X}} = \left[ {\begin{array}{*{20}{c}} m&{\displaystyle\sum\limits_{i = 0}^m {{x_i}} }& \cdots &{\displaystyle\sum\limits_{i = 0}^m {x_i^n} } \\ {\displaystyle\sum\limits_{i = 0}^m {{x_i}} }&{\displaystyle\sum\limits_{i = 0}^m {x_i^2} }& \cdots &{\displaystyle\sum\limits_{i = 0}^m {x_i^{n + 1}} } \\ \vdots & \vdots & \ddots & \vdots \\ {\displaystyle\sum\limits_{i = 0}^m {x_i^n} }&{\displaystyle\sum\limits_{i = 0}^m {x_i^{n + 1}} }& \cdots &{\displaystyle\sum\limits_{i = 0}^m {x_i^{2n}} } \end{array}} \right] \text{，} {\boldsymbol{Y}} = \left[ {\begin{array}{*{20}{c}} {\displaystyle\sum\limits_{i = 0}^m {{y_i}} } \\ {\displaystyle\sum\limits_{i = 0}^m {{x_i}{y_i}} } \\ \vdots \\ {\displaystyle\sum\limits_{i = 0}^m {x_i^n{y_i}} } \end{array}} \right] $$ 根据已知离散轨迹点集
$ ({x_i},{y_i}) $ ，计算待定参数为$$ {{\boldsymbol{A}}^T} = {{\boldsymbol{X}}^{ - 1}}{\boldsymbol{Y}} $$ (9) Step5：将式（9）代入式（4），即可获取所拟合曲线的多项式。
2.2 三种平面线形拟合
根据铁路平面线形的特点，可将拟合曲线多项式分为直线线形、圆曲线及缓和曲线3种，其具体拟合方法如下。
2.2.1 直线线形拟合
设直线参数方程为
$ y = ax + b $ ，根据直线上的$m$ 个观测点坐标$({x}_{i},{y}_{i})$ , i=1,2,···, m，根据LS原理，可求得其系数为$$ \left\{ \begin{gathered} b = \frac{{k\displaystyle\sum\limits_i {{x_i}{y_i} - \displaystyle\sum\limits_i {{x_i}} \displaystyle\sum\limits_i {{y_i}} } }}{{k\displaystyle\sum\limits_i {x_i^2 - (\displaystyle\sum\limits_i {{x_i}{)^2}} } }} = \frac{{\overline{xy} - \overline{x} \cdot \overline{y} }}{{\overline {{x^2}} - {{\overline x }^2}}} \\ a = \frac{{\displaystyle\sum\limits_i {x_i^2} \displaystyle\sum\limits_i {{y_i}} - \displaystyle\sum\limits_i {{x_i}{y_i}} \displaystyle\sum\limits_i {{x_i}} }}{{k\displaystyle\sum\limits_i {x_i^2 - (\displaystyle\sum\limits_i {{x_i}{)^2}} } }} = \overline y - b\overline x \\ \end{gathered} \right. $$ (10) 将式（10）中的a、b代入
$ y = ax + b $ ，即可获得当前目标直线方程。2.2.2 圆曲线拟合
设圆曲线参数方程为
$ {R^2}{\text{ = }}{(x - {x_0})^2} + {(y - {y_0})^2} $ ，其中，$ ({x_0},{y_0}) $ 为圆心坐标；$ R $ 为圆曲线半径。根据LS原理对曲线上的各坐标点$ ({x_i},{y_i}) $ 进行拟合，残差平方和函数$ Q $ 为$$ Q = \sum\limits_{i = 1}^m {{{[{{({x_i} - {x_0})}^2} + {{({y_i} - {y_0})}^2} - {R^2}]}^2}} $$ (11) 由LS原理约束条件可知
$$ \frac{{\partial Q}}{{\partial {x_0}}} = \frac{{\partial Q}}{{\partial {y_0}}} = \frac{{\partial Q}}{{\partial R}} = 0 $$ (12) 联立式（11）和式（12），可求解相关参数为
$$ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left\{ \begin{gathered} R = \sqrt {{x_0}^2 - 2\overline x {x_0} + {y_0}^2 - 2\overline y {y_0} + \overline {{x^2}} + \overline {{y^2}} } \\ {x_0} = \frac{{(\overline {{x^2}} \overline x + \overline x \overline {{y^2}} - \overline {{x^3}} - \overline {x{y^2}} )({{\overline y }^2} - \overline {{y^2}} ) - (\overline {{x^2}} \overline y + \overline y \overline {{y^2}} - \overline {{y^3}} - \overline {{x^2}y} )(\overline x \overline y - \overline {xy} )}}{{2({{\overline x }^2} - \overline {{x^2}} )({{\overline y }^2} - \overline {{y^2}} ) - 2{{(\overline x \overline y - \overline {xy} )}^2}}} \\ {y_0} = \frac{{(\overline {{x^2}} \overline y + \overline y \overline {{y^2}} - \overline {{y^3}} - \overline {{x^2}y} )({{\overline x }^2} - \overline {{x^2}} ) - (\overline {{x^2}} \overline x + \overline x \overline {{y^2}} - \overline {{x^3}} - \overline {x{y^2}} )(\overline x \overline y - \overline {xy} )}}{{2({{\overline x }^2} - \overline {{x^2}} )({{\overline y }^2} - \overline {{y^2}} ) - 2{{(\overline x \overline y - \overline {xy} )}^2}}} \\ \end{gathered} \right. $$ (13) 其中，
$\overline {{x^a}{y^b}} = \left( {\displaystyle\sum\limits_{i = 1}^m {x_i^ay_i^b} } \right)/m$ ，且$ a = 0,1,2,3 $ ；b = 0,1,2,3。代入求解即可获得目标圆曲线方程，2.2.3 缓和曲线拟合
设缓和曲线参数方程为
$ y = \dfrac{{{x^3}}}{{6R{l_0}}} $ ，其中，$ {l_0} $ 为缓和曲线长度。对缓和曲线参数方程采用三次多项式拟合，对各坐标点$ ({x_i},{y_i}) $ 进行LS拟合，则拟合方程为$$ y = a{x^3} + b{x^2} + cx + {{d}} $$ (14) 按2.1节求解方法，代入4个轨迹点值即可确定上式
$ a、b、c、d $ 这4个参数。2.3 引入自适应权值因子的最小二乘拟合方法
在卫星数据采集过程中，受设备条件及环境因素影响，往往会存在野值数据。在标准的最小二乘拟合方法中，并未消除这种数据的影响，会使拟合线形不够平滑、精度下降。因此，本文引入自适应权值因子来降低野值数据的影响，提高可靠轨迹数据的拟合权值，使拟合线形更符合实际线路情况。
2.3.1 自适应权值因子的确定
若观测轨迹点在
$ t $ 时刻以前满足测试数据的噪声分布，而在$ t $ 时刻出现较大偏差，则可将$ t $ 时刻的观测数据视作是叠加在常规观测值上的一个野值，此时观测值$ {y_t}' $ 为$$ {y_t}' = {y_t} + \omega $$ (15) 其中，
$ \omega $ 为与野值相关的偏差分量，$ {y_t} $ 为平稳状态下的理论观测值。此时残差估计值为$$ {\delta _t} = C({x_t}) - {y_t}' = C({x_t}) - \left( {{y_t} + \omega } \right) $$ (16) 铁路平面线形拟合是已知整体轨迹数据的后处理过程，与轨迹观测点的时序无关，故定义当前测点与拟合曲线的相似耦合度因子
$ \tau (t) $ 为$$ \left\{ \begin{gathered} \tau \left( t \right) = \rho (t)\frac{{{{\left| \delta \right|}_{\max }} - {\delta _t}}}{{\sigma \left( \delta \right)}} \\ \rho \left( t \right) = r\left( {\delta _{t - L}^t,\delta _{t - 1 - L}^{t - 1}} \right) \\ \end{gathered} \right. $$ (17) 其中，
$ \rho (t) $ 为两轨迹序列残差的相关系数；$ \delta _{t - L}^t $ 为包含当前数据点的轨迹序列；$ \delta _{t - 1 - L}^{t - 1} $ 不含当前数据点的相邻轨迹序列；$ L $ 为轨迹序列长度，依据采样周期进行相应调节。$ \tau \left( t \right) $ 反映了相邻序列间的相似程度，相关系数越高，则该观测点序列平滑，相关系数低，即判断当前点为野值数据。对残差进行归一化为
$$ \eta = \frac{1}{{{{\left| \delta \right|}_{\max }} - {{\left| \delta \right|}_{\min }}}} $$ (18) 其中，
$ {\left| \delta \right|_{\max }} $ 为残差序列最大值的绝对值，$ {\left| \delta \right|_{\min }} $ 为残差序列最小值的绝对值。故权值因子$ {\lambda _t} $ 与残差$ {\delta _t} $ 的关系为$$ {\lambda _t} = {\left(\frac{{{{\left| \delta \right|}_{\max }} - {\delta _t}}}{{{{\left| \delta \right|}_{\max }} - {{\left| \delta \right|}_{\min }}}}\right)^{\tau (t)}} = \eta {\left( {{{\left| \delta \right|}_{\max }} - {\delta _t}} \right)^{\tau (t)}} $$ (19) 当观测点
$ ({x_t},{y_t}) $ 与对应拟合曲线$ l $ 的残差$ {\delta _t} $ 越大时，观测点与拟合轨迹相似耦合程度越低，权值因子$ {\lambda _t} $ 随之减小，降低观测点的可信度；反之，当残差$ {\delta _t} $ 较小时，$ {\lambda _t} $ 增大，提高观测点的可信度，因此，可通过$ {\lambda _t} $ 对野值进行自适应修正。2.3.2 改进最小二乘线形拟合算法流程
自适应权值因子改进后的最小二乘目标拟合函数为
$$ \left\{ \begin{gathered} \begin{array}{*{20}{c}} {\min }&{\left\| \delta \right\|_2^2} \end{array} \\ \left\| \delta \right\|_2^2 = \sum\limits_{t = 0}^m {{\lambda _t}\delta _t^2} = \sum\limits_{t = 0}^m {{\lambda _t}{{\left[ {C({x_t}) - {y_t}} \right]}^2}} \\ \end{gathered} \right. $$ (21) 自适应权值因子改进的最小二乘算法流程如下。
（1）按照标准最小二乘算法步骤拟合初始曲线；
（2）对观测轨迹点
$ {O_t} $ 的拟合残差序列${\delta _t} (t = 1, 2, \cdots ,m)$ 进行计算；（3）根据式（17）、（18）求解相似耦合度因子
$ \tau \left( t \right) $ 及归一化系数$ \eta $ ，并由式（19）计算得到自适应权值因子$ {\lambda _t} $ ；（4）根据自适应权值因子
$ {\lambda _t} $ 改进拟合参数，根据2.1节拟合方程求解，获取轨迹分段线形。3 试验验证及分析
3.1 试验数据准备
为验证本文拟合方法的有效性，采用PwrPak7-E1组合导航系统，测得兰州交通大学至北环路的车辆GNSS轨迹数据，并进行验证，线路全长约5.7 km，共计800个测点，对数据进行经纬度坐标的UTM（Universal Transverse Mercator）平面投影转换，转换后的轨迹平面线形如图4所示。
3.2 线形识别及拟合结果
参照文献[12]，采用滑动平均滤波法对其轨迹各测点的方位角进行处理，如图5所示，已知直线路段曲率恒为零，设定
$\dfrac{1}{1\;000}·\dfrac{{\text{π}} }{180}$ $（度 /m）$ 为直线及曲线的划分阈值，将直线路段属性设定为1，曲线路段属性设为0。可对车辆轨迹的分段进行初步划分，该车辆轨迹可分为17段，包含9个曲线段，8个直线段，如图6所示。根据2.2节的拟合公式，分别对划分好的轨迹段进行拟合，可得到相应的线形及参数。拟合后的轨迹曲率特征如图7所示，拟合后的平面线形的分布如图8所示。拟合误差表示测量数据在拟合轨迹和真实轨迹中投影点的残差，其值代表了平面线形的拟合精度。本文将拟合误差绝对值的均值（AVG）、最大值（MAX）、方差（VAR）、均方误差（MSE）作为衡量指标，与传统最小二乘拟合方法进行对比，拟合误差相关参数如表2所示。
表 2 算法性能指标对比性能指标 标准LS 改进LS AVG 1.0421 0.8213 MAX 1.6542 0.9356 VAR 0.3524 0.0572 MSE 0.5446 0.3741 由表2可知，引入自适应权值因子改进的LS拟合方法，在拟合精度上更具优势，可有效抑制野值数据对拟合平滑度的影响，使轨迹平面线形与真实线路更为接近。算法可对线路的直线、缓和曲线及圆曲线3种平面线形进行有效识别并拟合，通过线形分界点及对应线形拟合参数对轨迹数据进行约简表示的方法适用于数字轨道地图的构建过程。
4 结束语
本文基于铁路线路平面线形的特点，采用方位角近似估计曲率的方法对轨迹平面线形进行初步识别分类；引入自适应权值因子改进的LS方法进行分段轨迹的曲线拟合；并通过实测车辆轨迹数据进行验证。本文方法能够有效对3种铁路平面线形进行识别，改进的LS方法可降低野值数据拟合权值，从而提高轨迹拟合平滑度，比传统LS方法拟合精度更高。
-
[1] OTEGUI J, BAHILLO A, LOPETEGI I, et al. A survey of train positioning solutions [J]. IEEE Sensors Journal, 2017, 17(20): 6788-6797. DOI: 10.1109/JSEN.2017.2747137
[2] 夏 青,杨剑锋. 数字轨道地图线路分段表示方法研究 [J]. 铁路计算机应用,2012,21(4):9-11. DOI: 10.3969/j.issn.1005-8451.2012.04.003 [3] 倪晓林,杨 妮,张 东. 列控数字轨道地图自动生成算法研究 [J]. 铁道运营技术,2010,16(1):24-27. DOI: 10.3969/j.issn.1006-8686.2010.01.009 [4] 左自辉,王开锋,许 聪,等. 生成高精度轨道电子地图的数据处理方法 [J]. 中国铁道科学,2016,37(4):134-138. DOI: 10.3969/j.issn.1001-4632.2016.04.21 [5] 龚 利,沙建领,赵 超,等. 基于北斗定位技术的铁路机车轨道电子地图生成算法 [J]. 计算机系统应用,2019,28(6):172-177. DOI: 10.15888/j.cnki.csa.006945 [6] 刘 江,蔡伯根,唐 涛,等. 基于GPS的列控轨道地图数据生成方法研究 [J]. 测绘学报,2011,40(1):111-117. [7] 陈德旺,蔡伯根,王 剑,等. 轨道交通GPS数据约简的数学模型与算法研究 [J]. 铁道学报,2008(4):116-119. DOI: 10.3321/j.issn:1001-8360.2008.04.023 [8] 曾 强,陈德旺,王丽娟,等. 基于主曲线和自适应半径的多GPS轨迹数据融合算法 [J]. 铁道学报,2015,37(2):46-51. DOI: 10.3969/j.issn.1001-8360.2015.02.007 [9] 陈德旺. 铁路卫星定位数据的智能处理[M]. 北京: 北京交通大学出版社, 2014. [10] Camacho-Torregrosa F J, AM Pérez-Zuriaga, JM Campoy-Ungría, et al. Use of Heading Direction for Recreating the Horizontal Alignment of an Existing Road [J]. Computer-Aided Civil and Infrastructure Engineering, 2015, 30(4): 282-299. DOI: 10.1111/mice.12094
[11] Winter H , Luthardt S , Willert V , et al. Generating Compact Geometric Track-Maps for Train Positioning Applications[C]//2019 IEEE Intelligent Vehicles Symposium (IV), June 09-12, 2019, Paris, France. New York, USA: IEEE, 2019.
[12] 陶维杰,蔡伯根,王 剑,等. 数字轨道地图平面线形特征提取方法研究 [J]. 铁道学报,2019,41(9):81-87. DOI: 10.3969/j.issn.1001-8360.2019.09.011 [13] 陈明晶,方源敏,陈 杰. 最小二乘法和迭代法圆曲线拟合 [J]. 测绘科学,2016,41(1):194-197,202. DOI: 10.16251/j.cnki.1009-2307.2016.01.038 -
期刊类型引用(1)
1. 陈丹，杨蔼露，张定娆. 基于空间尺度的道路网地图智能制图技术研究. 自然资源信息化. 2024(02): 57-61 . 
百度学术
其他类型引用(2)
下载:
计量
- 文章访问数: 112
- HTML全文浏览量: 282
- PDF下载量: 21
- 被引次数: 3
