Short-term passenger flow prediction of urban rail transit based on optimized GA-SLSTM
-
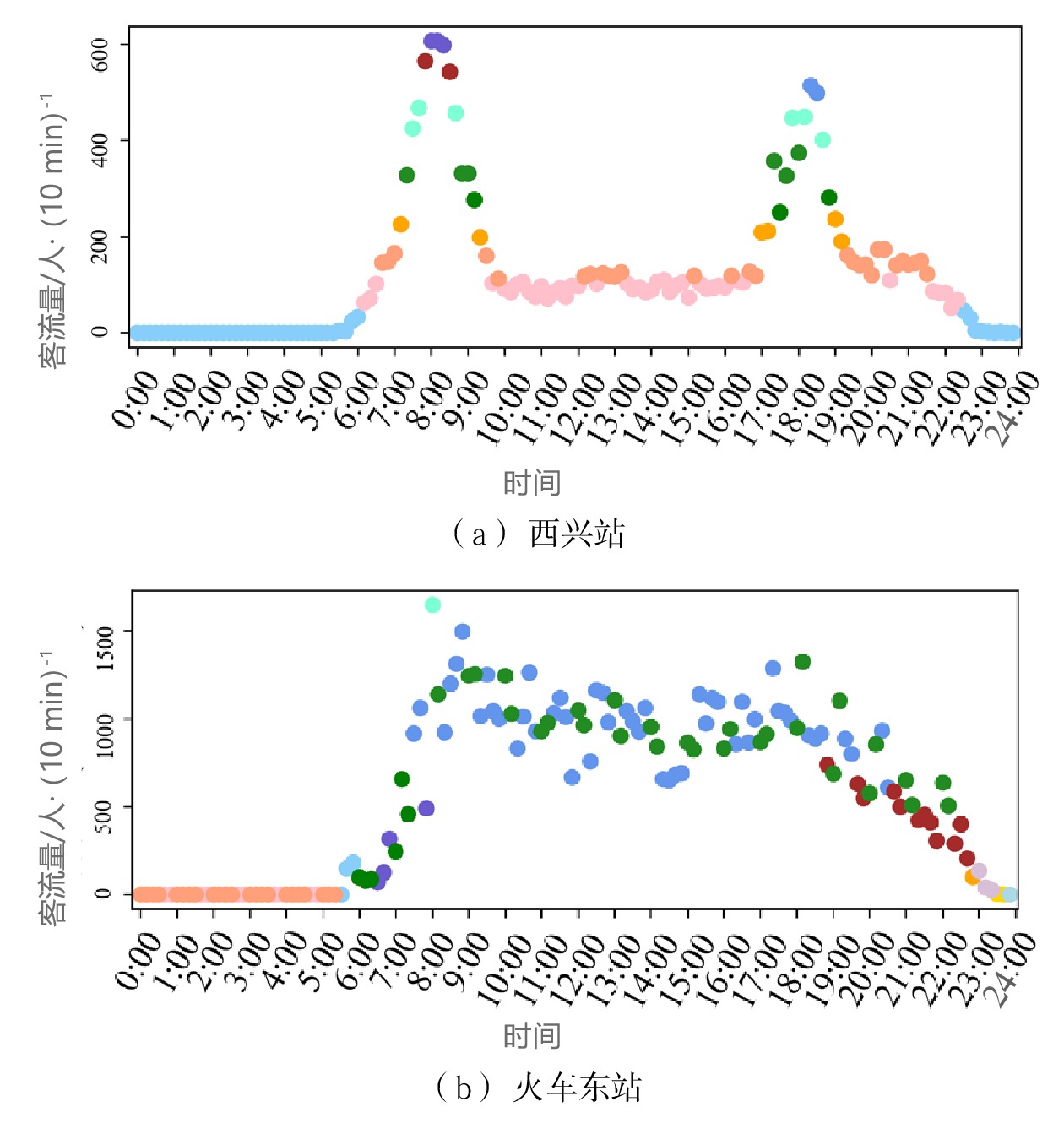
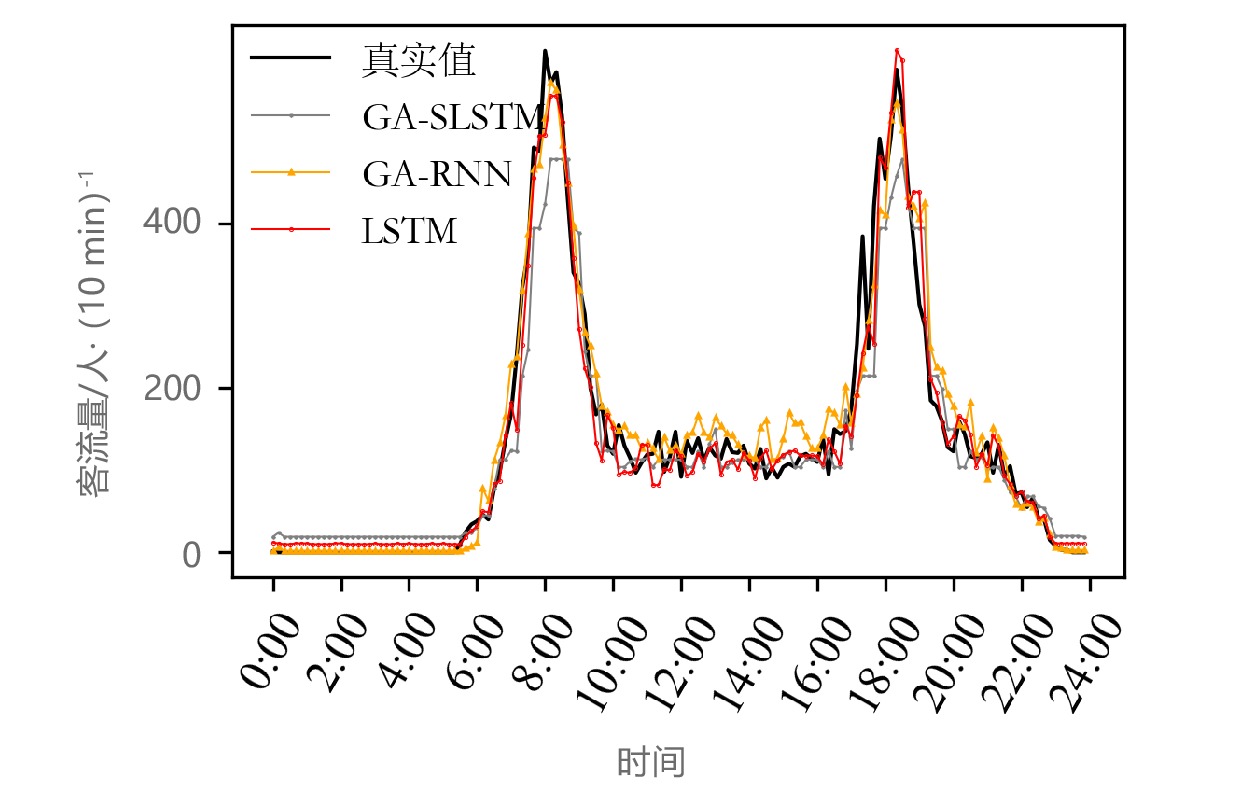
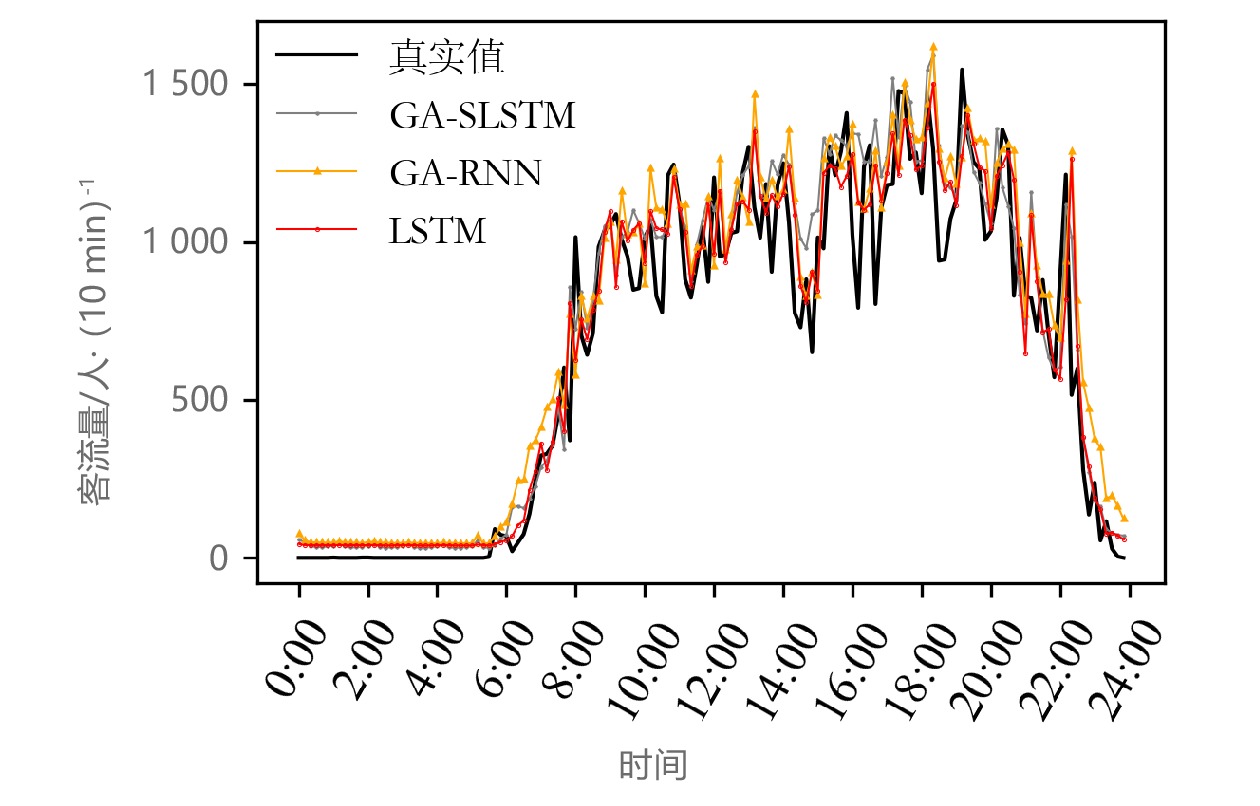
摘要: 城市轨道交通短时客流预测可为相关运营部门实时调整行车调度、提高运营效率提供重要的决策依据,为乘客提供合理出行建议。因此,针对具有非线性和随机性等特性的地铁进出站短时客流预测问题,文章在堆叠式长短时记忆(SLSTM,Stacked Long Short Term Memory)模型的基础上,引入遗传算法(GA,Genetic Algorithm),构建了GA-SLSTM预测模型。以10 min为预测粒度对地铁历史运营数据进行整理,分析了客流变化特征,并将其与GA-循环神经网络(RNN ,Recurrent Neural Network)模型和LSTM模型的预测效果进行对比。GA-SLSTM预测模型对普通站点和换乘站点预测值的决定系数R2的平均值分别达到0.95和0.90,预测值对真实值的拟合效果较好,预测误差低于其他2种模型,证明该方法可提高地铁短时客流预测的准确性。
-
关键词:
- 城市轨道交通 /
- 短时客流预测 /
- 堆叠式长短时记忆(SLSTM)模型 /
- 智能交通 /
- 遗传算法
Abstract: Short-term passenger flow prediction of urban rail transit can provide important decision-making basis for relevant operation departments to adjust traffic scheduling in real time and improve operation efficiency, and provide reasonable travel suggestions for passengers. Therefore, aiming at the prediction of short-term passenger flow in and out of subway stations with nonlinear and random characteristics, this paper introduced Genetic Algorithm (GA) on the basis of Stacked Long Short Term Memory (SLSTM) network, and constructed a GA-SLSTM prediction model. The paper sorted out the historical operation data of the subway granularity of 10 minutes, analyzed the characteristics of passenger flow changes, and compared their prediction effects with GA-RNN and LSTM network models. The average value of the decision coefficient R2 of GA-SLSTM method for the predicted values of ordinary stations and transfer stations reached 0.95 and 0.90 respectively. The predicted value has a good fitting effect on the real value, and the prediction error is lower than the other two models, which proves that this method can improve the accuracy of short-term passenger flow prediction of subway. -
铁路电子客票已于2020年6月20日在全国普速铁路推广实施[1],是客运提质的基础工程,推动客运智能发展的重要载体,以及解决旅客在票务、进站、候车、乘车、出站、换乘全过程信息化服务的必要手段。在电子客票的推行进程中,为便于旅客乘降组织的智能化发展,铁路客运部门已于2018年通过搭建人脸识别平台,支持铁路实名制进站核验系统,解决人证一致性自动检验的问题[2]。但该场景下的人脸识别技术,属于1v1模式,而刷脸出站、铁路车站内刷脸查询[3]等场景,需要研究基于1 v N模式的人像检索技术及其应用[4]。
2020年,铁路客票系统团队首次开展了基于人像检索技术的研究,铁路人像检索平台的建设主要满足车站无障碍式刷脸办理业务的需求,并实现无证件、无二维码仅通过一张“脸”知行程的功能。铁路人像检索平台上线之初,通过手动配置能够满足业务的基本需要,但随着业务场景应用范围的不断扩大,业务运维效率低下、操作流程复杂等问题日益突出,平台的流量调度模块逐渐臃肿,需要进一步优化平台的流量调度机制。
1 人像检索平台概述
平台主要应用于铁路客运场景,对终端获取的现场人脸进行人像检索,进而识别旅客身份,关联旅客车票信息,实现旅客在特定场景下的“无障碍”式出行。平台的搭建需关联多个铁路内的信息系统资源,实现人像检索算法的集成与业务逻辑的封装。
1.1 平台微服务功能
人像检索平台的软件设计采用微服务架构,基于开源的ServiceComb微服务框架[5]进行构建。平台的微服务主要包含以下几部分。
1.1.1 公共服务
公共服务包括公安服务、图片服务、配置服务等。公安服务主要通过实名制信息获取旅客的证件照;图片服务主要实现人像证件照、现场照等图片在文件系统中的增、删、查、改;配置服务针对Apollo配置中心中的配置,对其它微服务进行配置热更新。
1.1.2 基础服务
主要包括初始化、心跳、日志接收等简单的基础业务服务。初始化实现对终端设备业务开展前的鉴权认证;心跳负责监控终端设备的存活状态;日志接收实现了终端业务开展时日志向平台的实时上报,便于统计分析与故障运维等。
1.1.3 外部对接
外部对接包括管控服务、实名制消费、席位数据查询等。管控服务对开展人像检索业务的车站进行定义与维护;实名制消费用于接收电子客票推送的旅客实名制信息,并根据规则进行人像建桶;席位数据查询实现根据实名制信息查询电子客票,进而获得旅客车票信息的功能。
1.1.4 业务服务
业务服务包括人像检索、错误标注、证件类查询等。人像检索实现了在人脸桶中根据人脸现场照检索人像底库,获取对应旅客标识及车票、候车等信息的功能;错误标注用于现场旅客对人像检索结果确定非本人时,根据证件进行业务查询并响应,同时记录现场人像用于后续的算法精进;证件类查询实现在人像检索失败后,通过识读证件实名制信息,直接向电子客票集群获取旅客车票信息的功能。
1.1.5 导航服务
导航服务根据车站电报码或列车全车次信息,实现代理地址的路由与导航。为提升人像检索的检索效率,减少内部资源加载时磁盘I/O的消耗。人脸桶、人像检索算法、人像检索逻辑调用等均处于同一物理位置,因此对人脸桶创建与维护时的地址路由、人像检索业务开展时服务地址寻址等,均通过导航服务动态代理来实现。
1.2 平台技术架构
人像检索服务平台的开发,使用ServiceComb实现一整套微服务的框架。各微服务之间弱耦合,且内部以gRPC协议互联,所有微服务通过ServiceComb注册中心统一管理,通过Apollo配置中心统一配置[6],并以Docker容器化方式运行[7]。平台的技术架构,如图1所示。
(1)接入层:解析多种消息协议,实现多服务的负载均衡与统一注册管理等。
(2)服务层:通过Apollo配置中心,区分生产环境与测试环境,同时内部组建微服务集群,实现业务逻辑。内部所有业务逻辑集群,均通过导航服务进行分发。所有集群日志通过ELK进行搜集、过滤与存储,基于Kibana实现分析与展示[6],利用DingTalk进行实时告警。
(3)资源层:整合人像检索平台外部相关资源,主要包括铁路电子客票集群、铁路公安系统、人脸识别算法、管控平台及站车无线交互平台等。
1.3 人像检索平台问题描述
1.3.1 手动配置,运维难度大
人像检索平台建设初期,导航服务作为服务入口,承担着地址路由、流量分发及请求重定向等功能,其中所有的导航规则全部在Apollo配置文件中定义,该配置文件要手动进行增加、删除等维护。当车站需要开通人像检索业务时,除需在业务管控定义中进行新增车站信息以外,还需通过Apollo配置中心,手动添加该车站相关的导航信息;当车站停用人像检索业务时,又需手动删除配置中该车站的导航规则。因此,当开通人像检索业务的车站较少时,系统可勉强运维,但当需开通人像检索业务的车站较多时,配置文件会变得异常臃肿,手动运维复杂度显著提升。
1.3.2 流量负载不均衡
既有方式未能考虑车站客流量大小不同时,因流量差异而产生的服务并发不均衡问题。既有的铁路人像检索平台服务资源分配不合理,日均客流量5000人次的车站与日均客流量50000人次的车站,其对应的平台资源不应相同,不应以最高客流量的车站作为其它车站资源划分的标准,以满足并发冗余等。因此,平台的建设需要评估车站客流量的大小,实现流量的智能调度与均衡路由,合理分配系统服务资源。
2 平台流量智能调度
流量智能调度的设计摒弃既有需要手工完成导航定义的操作方式。当车站需要新开通或注销人像检索业务时,仅需修改车站管控定义,即可在平台完成车站的导航规则更新流程。在保持原有业务导航的前提下,人像检索业务中对车站导航规则的维护将更加智能,显著降低运维复杂度。
2.1 配置改造
业务应用服务运行于容器Docker中,实际业务处理均可在容器启动时指定地址与端口,因此平台所有业务的逻辑处理,都具有资源池的概念。配置改造中,不再指定具体车站的标识与应用地址,转为仅根据业务场景指定资源,实际车站的路由选择由导航服务进行处理。
例如,平台支持站内刷脸查询、刷脸出站等业务,在配置中,针对不同的业务场景,记录所有利用的资源,多个资源以逗号作为分割,形成场景地址资源池。
刷脸查询机、刷脸机器人等业务资源地址配置如下:
station.on.route.adress =IpA:porta,IpB:portb,IpC:portc
刷脸出站业务资源地址配置如下:
station.train.route.adress=IpZ:portz,IpY:porty,IpX:portx
实际导航时,先对业务场景进行分析,获取资源池中定义的相应资源,此时获取的资源暂与车站无关,再结合车站日均客流量的大小,分析如何均衡且充分的利用相关资源。
2.2 新增数据表
假设铁路各类车站中,单车站日客运量最大为12万人,对不同车站的日客流量进行分析[8],确定车站等级,便于进行人像检索业务的流量合理调度,车站日客流量预估及级别定义如表1所示。
表 1 平台车站等级定义前日客流量/万 当日预估客流量/万 车站等级 0~2 0~3 1 2~3 3~4.5 2 3~4 4.5~6 3 4~5 6~7.5 4 5~6 7.5~9 5 6~7 9~10.5 6 7+ 10.5+ 7 表1中,当日客流量的评估一般根据前日客流量放大1.5倍进行冗余考虑。车站等级划分为7个级别,随着客流量的增加,车站等级逐渐增高,等级越高,导航实现时业务寻址的权重越大,实际业务访问的请求越多,该车站每日生成的人脸底库的个数越多。据此为车站的导航记录设计导航寻址数据表,如表2所示。
表 2 新增导航记录表名称 类型 说明 station_telcode varchar 车站电报码 station_tag varchar 车站标识(on:发站,off:到站) weight Int 车站流量权重(1~7,与等级对应,等级越高,权重越大) route varchar 导航路由地址 ext1 varchar 扩展字段1 ext2 varchar 扩展字段2 ext3 varchar 扩展字段3 2.3 依托权重的调度策略
不同铁路车站的日客流量不同,在人像检索的定义中该车站的权重就不同。如图2所示,业务流量根据导航规则进行路由时,基于车站电报码获取对应的权重,并结合Apollo中的地址池对资源进行分配,将检索权重值较小的车站进行业务合并,自动做到服务资源的合理分配。
假设配置Apollo中的路由地址池未在导航记录表中用尽,则将未使用的地址直接分配给新开通人像检索业务的车站使用。若路由地址池中的所有导航地址均已在导航记录表中使用,导航服务则根据传入的车站电报码,评估该车站的权重等级。根据权重等级,计算路由地址之间的权重总和,并取权重之和最小的地址作为此次导航地址进行分配,如果导航地址的权重之和相同,随机选取一个地址作为路由地址进行导航。
2.4 流量调度案例分析
假设Apollo中的业务资源地址配置为:
station.on.route.adress =IpA:porta,IpB:portb,Ipc:portc
导航服务会根据导航记录表中的数据,计算每个导航地址下分配的车站码权重之和,例如:
IpA:porta下已经分配的车站电报码列表为[QIP,VAP],权重级别分别为2、3,即IpA:porta的权重总和为5;
IpB:portb下已经分配的车站电报码列表为[QBP,VJP],权重级别分别为4、5,即IpB:portb的权重总和为9;
Ipc:portc下已经分配的车站电报码列表为[BXP,IZP,BJP],权重级别分别为2、1、6,即Ipc:portc的权重总和为9。
此时权重之和最小为5的地址为IpA:porta,导航服务会将其分配给新开通人像检索业务的车站电报码,并进行业务导航。
3 结束语
本文通过对车站的日客流量进行预测,定义车站等级,进而形成权重,通过权重均衡路由地址池中资源,并分配给相关车站,构建铁路人像检索平台智能流量调度,保障了平台的流量分发与路由地址管理,降低了运维复杂度,显著提升了平台的研发与运维效率。目前,虽已实现平台的流量智能分配,但仍存在一些不足,导航后置的业务处理服务若出现故障,仍需对调度信息进行手动修改,尚未能实现故障自愈机制,未来研究需在满足业务智能化发展的同时,进一步提升系统建设的鲁棒性。
-
表 1 西兴站2个星期之间客流Spearman相关系数
星期一 星期二 星期三 星期四 星期五 星期六 星期日 上个星期一 0.976 0.968 0.975 0.971 0.955 0.778 0.623 上个星期二 0.979 0.972 0.976 0.975 0.952 0.759 0.596 上个星期三 0.970 0.972 0.973 0.965 0.955 0.784 0.631 上个星期四 0.961 0.974 0.970 0.963 0.957 0.776 0.628 上个星期五 0.955 0.956 0.952 0.951 0.972 0.806 0.658 上个星期六 0.768 0.776 0.775 0.778 0.789 0.935 0.890 上个星期日 0.600 0.617 0.611 0.604 0.645 0.899 0.965 表 2 西兴站不同模型预测指标对比
指标GA-SLSTM GA-RNN LSTM MAE 1 平均值 22.42 22.90 38.08 36.84 25.70 23.46 2 21.19 40.83 23.99 3 25.08 31.60 20.70 RMSE 1 平均值 33.13 34.92 57.64 52.54 35.97 35.74 2 33.56 52.37 36.48 3 38.08 47.60 34.77 R2 1 平均值 0.95 0.95 0.86 0.88 0.94 0.94 2 0.95 0.88 0.94 3 0.94 0.90 0.95 表 3 火车东站不同模型预测指标对比
指标GA-SLSTM GA-RNN LSTM MAE 1 平均值 113.83 115.34 111.61 116.31 140.76 135.09 2 112.63 119.49 132.72 3 119.56 117.84 131.80 RMSE 1 平均值 157.16 161.03 163.32 162.25 185.80 178.70 2 159.12 155.55 175.27 3 166.82 167.89 175.04 R2 1 平均值 0.90 0.90 0.89 0.90 0.87 0.88 2 0.90 0.91 0.88 3 0.89 0.89 0.88 -
[1] Zhong C, Batty M, Manley E, et al. Variability in Regularity: Mining Temporal Mobility Patterns in London, Singapore and Beijing Using Smart-Card Data [J]. PLoS ONE, 2016, 11(2): e0149222. DOI: 10.1371/journal.pone.0149222
[2] Niu H, Zhou X. Optimizing urban rail timetable under time-dependent demand and oversaturated conditions [J]. Transportation Research Part C: Emerging Technologies, 2013(36): 212-230. DOI: 10.1016/j.trc.2013.08.016
[3] Wu J, Liu M, Sun H, et al. Equity-based timetable synchronization optimization in urban subway network [J]. Transportation Research Part C: Emerging Technologies, 2015(51): 1-18. DOI: 10.1016/j.trc.2014.11.001
[4] Keyu Wen, Guotang Zhao, Bisheng He, at el. A decomposition-based forecasting method with transfer learning for railway short-term passenger flow in holidays [J]. Expert Systems with Applications, 2022, 189(3).
[5] 陈深进,薛 洋. 基于改进卷积神经网络的短时公交客流预测 [J]. 计算机科学,2019,46(5):175-184. DOI: 10.11896/j.issn.1002-137X.2019.05.027 [6] 王秋雯,陈彦如,刘媛春. 基于卷积长短时记忆神经网络的城市轨道交通短时客流预测 [J]. 控制与决策,2021,36(11):2760-2770. DOI: 10.13195/j.kzyjc.2020.0501 [7] Liu Y, Liu Z, Jia R. DeepPF: A deep learning based architecture for metro passenger flow prediction [J]. Transportation Research Part C: Emerging Technologies, 2019(101): 18-34. DOI: 10.1016/j.trc.2019.01.027
[8] 仇建华,尚 凯,张亚岐,等. 基于相关向量机的城市轨道交通突发大客流预测 [J]. 大连交通大学学报,2019(1):13-17. DOI: 10.13291/j.cnki.djdxac.2019.01.003 [9] 惠 阳,王永岗,彭 辉,等. 基于优化PSO-BP算法的耦合时空特征下地铁客流预测 [J]. 交通运输工程学报,2021,21(4):210-222. [10] S. Hochreiter, J. Schmidhuber. Long Short-Term Memory [J]. Neural Computation, 1997, 9(8): 1735-1780. DOI: 10.1162/neco.1997.9.8.1735
[11] A. Graves, A. Mohamed, G. Hinton. Speech recognition with deep recurrent neural networks[C]// 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, May 26-31, 2013, Vancouver, BC, Canada. New York, USA: IEEE, 2013: 6645-6649.
-
期刊类型引用(1)
1. 吕占民,李士达,戴琳琳,宋春晓,董兴芝. 基于AR智能眼镜的免打扰列车验票应用研究. 铁路计算机应用. 2023(05): 64-67 .  本站查看
本站查看
其他类型引用(0)





 下载:
下载: