Calculation of maximum number of gathering passengers in railway station based on data fitting
-
摘要: 铁路车站旅客最高聚集人数是设计铁路客运站站房规模的主要依据之一。文章以成都东站为例，通过提取售/取票设备数据，统计旅客提前到站时间，采用对数正态、复合负指数、威布尔3种分布形式对旅客到站规律进行拟合分析，构建铁路车站最高聚集人数检算模型。试验结果表明，对数正态分布对铁路旅客提前到站规律拟合效果优于其他2种分布，基于最优拟合分布的计算结果更为精确，有利于精准掌握车站最高聚集人数。Abstract: The maximum number of gathering passengers in railway stations is one of the main basis for designing the scale of railway passenger stations. Taking Chengdu East Railway Station as an example, by extracting the data of ticket selling and collecting equipment, this paper calculated the time of early arrival of passengers, and used three distribution forms of logarithmic normal, compound negative index, and Weibull to fit and analyze the rules of passengers arrival, and constructed the checking model of the maximum number of gathering passengers in railway stations. The test results show that the fitting effect of logarithmic normal distribution on the early arrival rule of railway passengers is better than the other two distributions.The calculation result based on the optimal fitting distribution is more accurate, which is conducive to accurately grasp the maximum number of gathering passengers in railway stations.
-
根据《铁路旅客车站设计规范》（TB 10100—2018），铁路旅客车站最高聚集人数是确定铁路客站站房建筑面积的主要指标[1]。张天伟等人[2]、薛晓姣等人[3]研究了最高聚集人数的定义，并指出现有定义中存在的问题；诸多学者针对最高聚集人数的计算方法进行了研究，姚加林等人[4]结合概率统计法，通过计算机模拟对最高聚集人数进行预测；李建斌[5]使用概率统计法归纳分析了旅客出行特征及沿线旅客集散特性；张天伟等人[6]采用对数正态分布拟合旅客到达规律；叶玉玲等人[7]对原有的概率计算方法进行改进，论述高速铁路旅客候车时间分布规律符合对数正态分布；刘启钢等人[8]根据最高聚集人数的规律和旅客提前到站时间分布密度函数，对车站聚集人数进行解析计算；陈喜春等人[9]采用双参数威布尔分布对旅客到站时间进行曲线拟合，建立了铁路客运站旅客聚集人数通用公式；Oded等人[10]运用计算机建模的方法模拟了旅客进站流程及在车站内的活动情况。
综上，概率法具有普遍的适用性，且可较好地考虑旅客到站时间分布，未来工作中统计数据变更时也便于更新。既有文献中利用概率法计算车站最高聚集人数时，虽采用了各种拟合函数形式，但多以同一种分布为基础，计算整个车站的旅客聚集人数，未体现出对旅客到站规律差异的考量。
本文基于既有车站的旅客到站数据，探讨了旅客到站规律的差异性，通过对比研究的方式说明了概率法计算聚集人数时根据列车发车时刻等相关因素选取不同拟合函数的必要性。
1 旅客到站规律分析拟合
1.1 数据获取
本文通过提取售/取票机数据，搜集成都东站2019年2月2日的旅客乘车信息，共139385条记录，包含车次、到发站、票价及进站口等信息，并获得车站当日全部列车的实际出站时间。旅客在车站售/取票机取票即认为其进入车站范围，故本文以售/取票机显示的售取票时间，以及取票信息中对应车次的实际发车时间分别作为旅客在车站范围内滞留时间的起止点。
经统计，车站当日发送各类列车共202列。根据列车信息和旅客乘车数据中包含的车次号，将旅客乘车数据按所乘列车进行分类，考虑到其中6列列车当日上车总人数少于100，数据信息较少，易造成较大拟合误差，因此，筛选出旅客信息数据≥100条的196列列车的数据用于后续拟合分析。
1.2 旅客到站规律分析
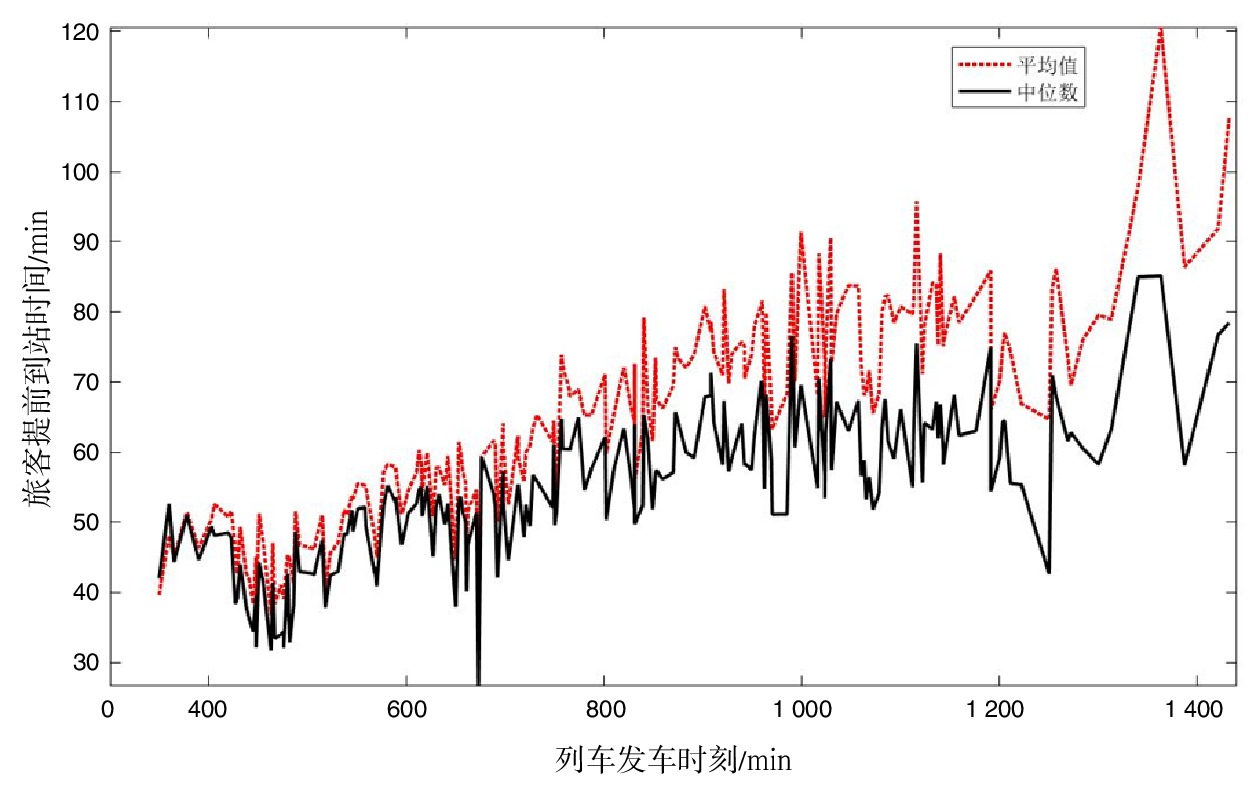
旅客到站规律受到诸多因素的影响。乘坐不同列车的旅客其到站规律往往存在差异。本文根据收集的成都东站相关数据，分析了旅客到站规律与列车出发时间的关联。单独分析每一列列车的旅客提前到站数据可发现，随着发车时间的变化，对应列车的旅客提前到站时长也会发生变化，变化趋势如图1所示。
图1中给出了不同发车时刻对应列车的旅客提前到站时间（涵盖了发车时间5：50～23：52的196列列车）。横坐标为列车发车时刻，即以0：00为计时起点，列车发车时刻距计时起点的分钟数；纵坐标为乘坐该时刻出发列车的旅客提前到站时间。
从整体趋势上看，随着列车发车时刻的推移，旅客提前到站时间的平均值和中位数值总体上呈现增大趋势，与实际生活中旅客出行习惯具有一定关联[11]。通常乘坐早上出发列车的旅客更倾向于根据列车发车时间有计划地安排其出行时间，在避免错过列车的同时，尽可能缩短候车时间，因此，其到站时间通常更靠近所乘坐列车的发车时间；而乘坐傍晚尤其是晚上9：00之后出发列车的旅客考虑到晚餐用餐时长、城市交通状况等因素，更倾向于为市内交通、铁路车站内检票候车等预留足够长的冗余时间，因此相较于早上出发的旅客，出现了到站时间更早，候车时间更长的现象。
1.3 旅客到站规律拟合
综上，乘坐不同列车的旅客到站规律可能不同。旅客到站规律是车站旅客最高聚集人数的重要影响因素。因概率法在计算旅客最高聚集人数时较好地考虑了旅客到站的概率分布及车站旅客列车开行方案，本文以概率法对旅客到站规律进行拟合。以5 min为间隔，按不同列车分别统计每一时间段内提前到站旅客人数，并根据对应列车的乘车总人数计算该时段提前到站人数的百分比，以此作为拟合的原始数据。
本文主要选取了对数正态分布、威布尔分布及复合负指数分布3种拟合函数对每一列列车的旅客到站规律进行拟合。拟合结果即为不同分布的概率密度函数
$ f(x) $ ，则$ t $ 时刻，已到站旅客占该列车总人数的比例为$$ {P}_{t}^{k}={\int }_{{t}_{0}}^{t}f\left(x\right)dx $$ (1) 且应满足
$$ {\int }_{{t}_{0}}^{T}f\left(x\right)dx=1 $$ (2) 其中，
$ P_t^k $ 表示第$ k $ 列车在$ t $ 时刻时已到站人数占该列车乘车总人数的比例；$ {t_0} $ 表示统计开始时刻，对应列车第1位旅客到站时间；$ T $ 表示统计结束时间，对应列车最后1位旅客到站时间。拟合旅客提前到站规律时，采用以下3种分布对旅客提前到站时间进行拟合。
对数正态分布概率密度函数为
$$ f\left(x\right)=\frac{1}{\sigma x\sqrt{2\pi }}\cdot exp\left\{\frac{-{(lnx-\mu )}^{2}}{2{\sigma }^{2}}\right\} $$ (3) 其中，
$ \mathrm{\sigma } $ 、$\mu$ 为对数正态分布的形状参数。威布尔分布的概率密度函数为
$$ f\left(x\right)=a\cdot b\cdot {x}^{b-1}\cdot \mathrm{e}\mathrm{x}\mathrm{p}(-a\cdot {x}^{b}) $$ (4) 其中，
${a}{、}{b}$ 为威布尔分布的形状参数。复合负指数分布的概率密度函数为：
$$ f\left(x\right)={c}_{1}\cdot ({e}^{-{c}_{2}x}-{e}^{-{c}_{3}x}) $$ (5) 其中，
$ {c}_{1}、{c}_{2}、{c}_{3} $ 是复合负指数分布的形状参数。本文将对同一列列车旅客提前到站时间分别用上述3种分布进行拟合，通过对比拟合评价指标，选取最佳拟合分布形式。
2 最高聚集人数计算
2.1 算法流程
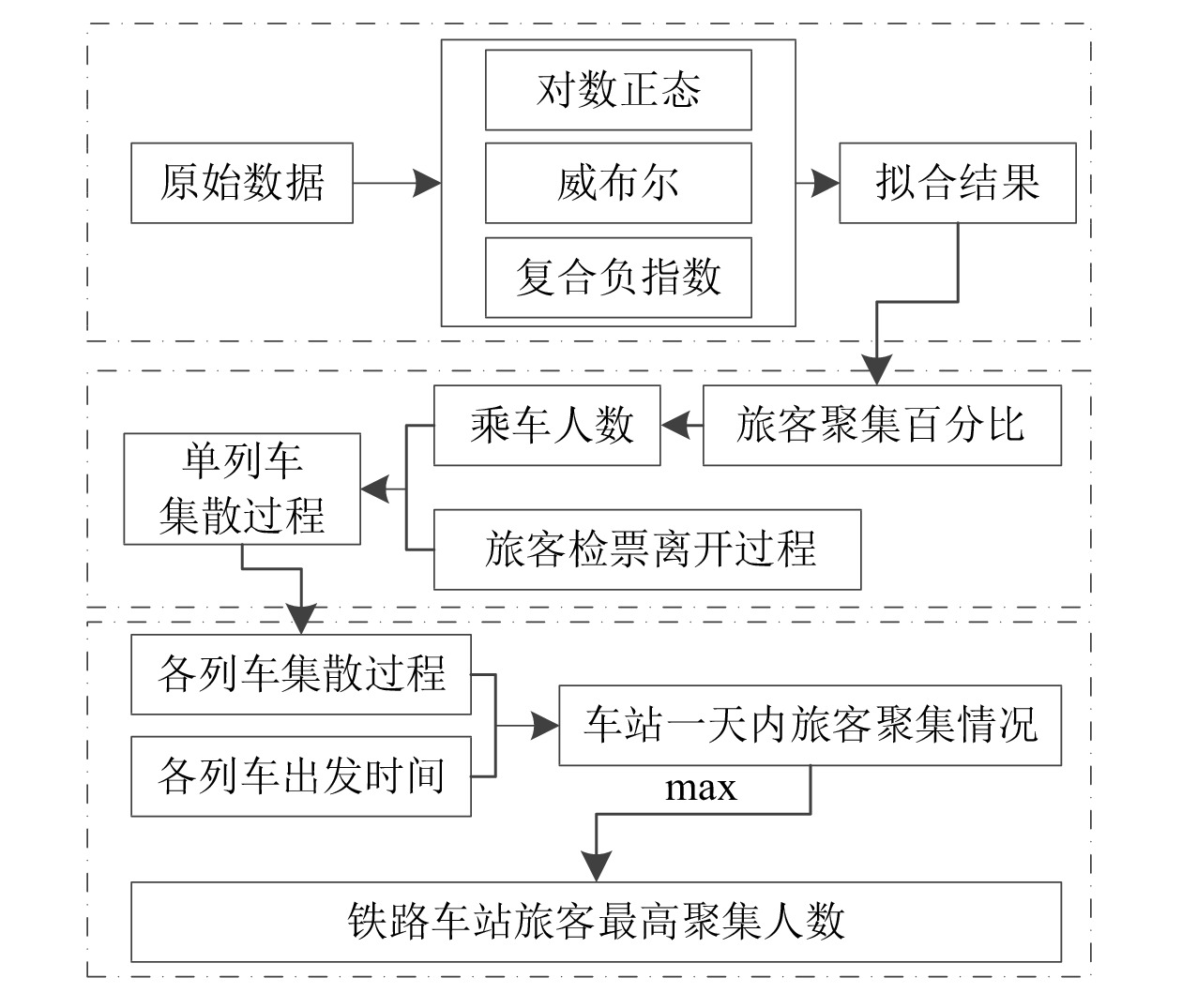
本文以成都东站数据为例，通过概率法确定车站旅客最高聚集人数的主要思路如图2所示，具体步骤如下。
（1）旅客到站规律拟合。本文设计3种数据拟合方法，分别基于最优分布、基于不同参数下的对数正态分布、基于相同分布，对原始数据进行拟合，确定旅客提前到站时间的概率密度函数。
（2）确定单列车旅客集散过程。利用概率密度函数计算出单列车乘客到站人数，假设旅客匀速检票乘车，即可确定单列列车旅客集散人数序列。
（3）确定车站旅客集散过程。计算该车站一天发送的所有列车旅客集散人数序列，根据列车发车时间，汇总列车旅客集散人数序列，得到车站一天内旅客聚集情况，即可得到最高聚集人数。
在研究旅客检票出发规律时，张天伟等人[12-13]通过调研某实际候车室旅客检票数据绘制了检票速度随时间的变化曲线，认为在计算旅客聚集人数时可以考虑做匀速处理，建议取70人/min～90人/min，并可将匀速检票时间适当延长，以减小检票速度下降带来的误差。据此，本文采用匀速方式处理旅客检票上车过程，设检票速度为80人/min。
2.2 案例分析
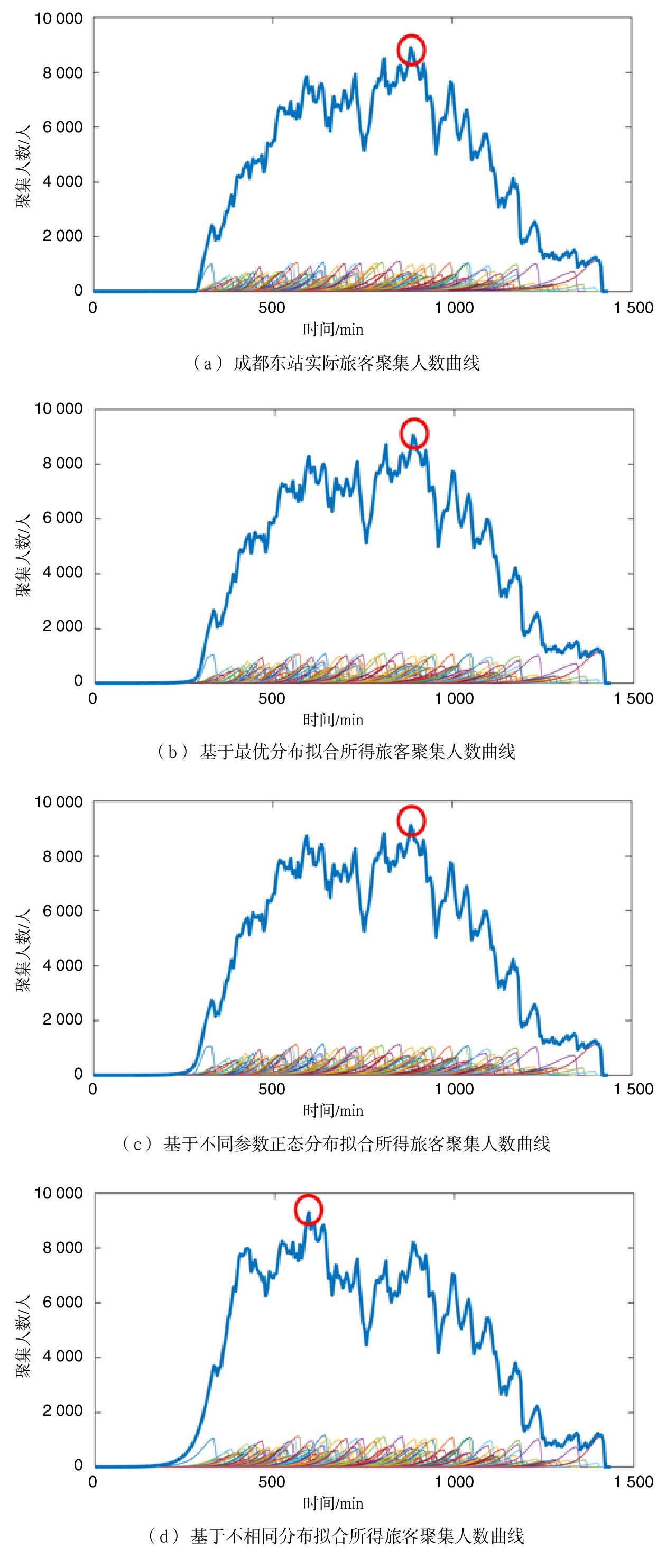
本文基于成都东站2019年2月2日实际旅客进站数据及实际列车开行方案数据，绘制了当日成都东站实际旅客聚集人数曲线。将旅客通过检票闸机进站数据按车次分类，并计算每5 min该车次旅客聚集人数和聚集人数百分比，得到该车次的旅客聚集曲线；再将该工作日内所有车次的旅客聚集曲线进行叠加，得到整个车站在该工作日的旅客聚集人数变化曲线，如图3（a）所示，作为参照组，其旅客最高聚集人数为8887人，出现在14：45～14：50时间段内，图中用红色圆圈标注。
2.2.1 基于最优拟合分布
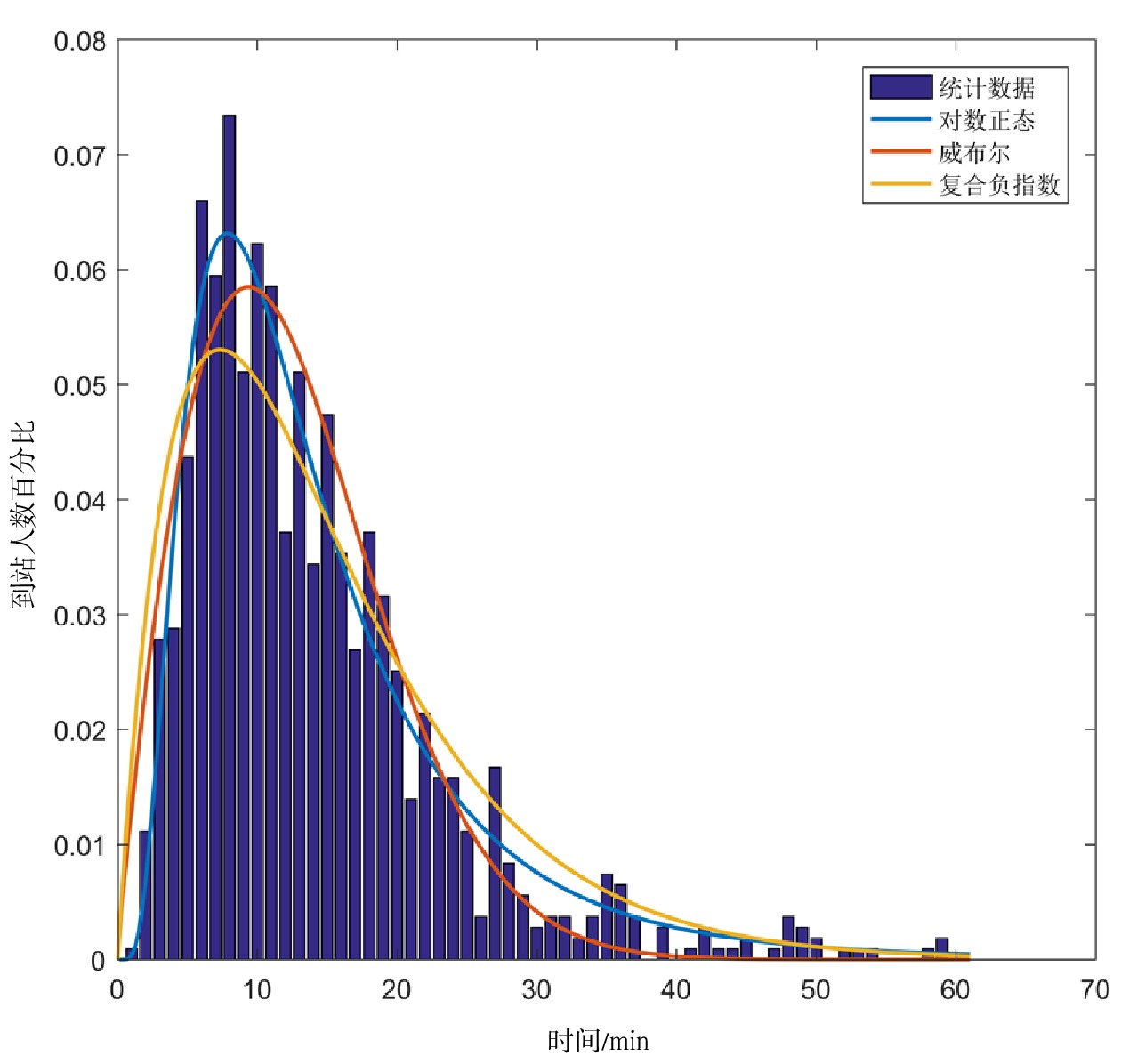
使用对数正态分布、威布尔分布及复合负指数分布分别对每一列列车的旅客提前到站数据进行拟合，计算不同拟合的拟合优度，即比较不同拟合条件下拟合优度评价指标，选取指标得分最高的拟合作为对应列车的最优拟合分布。本文以D5178次列车为例，分别采用1.3节中所述3种拟合方法对该列车的旅客到站情况进行拟合。拟合结果如图4所示，3种分布在一定程度上均可描述出旅客到站的大致趋势。拟合优度如表1所示，SSE、R2、RMSE分别表示误差平方和、可决系数和均方根误差。从表1可看出，3种分布均能较好地拟合D5178次列车旅客提前到站规律，且对数正态分布的拟合效果最好。
表 1 D5178次列车拟合结果对比指标 SSE R2 RMSE 对数正态 0.0013 0.9503 0.0046 威布尔 0.0021 0.9179 0.0059 复合负指数 0.0028 0.8879 0.0070 根据该拟合分布确定不同列车各时段已到站人数占总乘车人数百分比，从而模拟旅客到站规律。拟合结果如图3（b）所示。基于最优分布的拟合结果显示，由196列列车计算得到的成都东站旅客最高聚集人数为9042人，最高聚集人数出现在14：45～14：50时间段内。
2.2.2 基于不同参数的对数正态分布
利用3种分布进行拟合后发现，对超过77%的列车而言，对数正态分布是最优分布。在拟合旅客提前到站时间分布规律问题上具有更强适用性。根据不同参数下的对数正态分布，确定不同列车各时段已到站人数占总乘车人数百分比，从而模拟旅客到站规律，拟合结果如图3（c）所示。
基于不同参数的对数正态分布的拟合结果显示，由196列列车计算得到的成都东站旅客最高聚集人数为9120人，最高聚集人数出现在14：45～14：50时间段内。
2.2.3 基于相同分布
若不考虑乘坐不同列车的旅客到站规律的差异性，以同一分布函数（对数正态分布）拟合所有列车的旅客到站时间，拟合参数取各参数的平均值，根据该分布确定不同列车各时段已到站人数占总乘车人数百分比，从而模拟旅客到站规律，拟合结果如图3（d）所示。
基于完全相同分布的拟合结果显示，由196列列车计算得到的成都东站旅客最高聚集人数为9280人，最高聚集人数出现在9：55～10：00时间段内。
2.3 对比分析
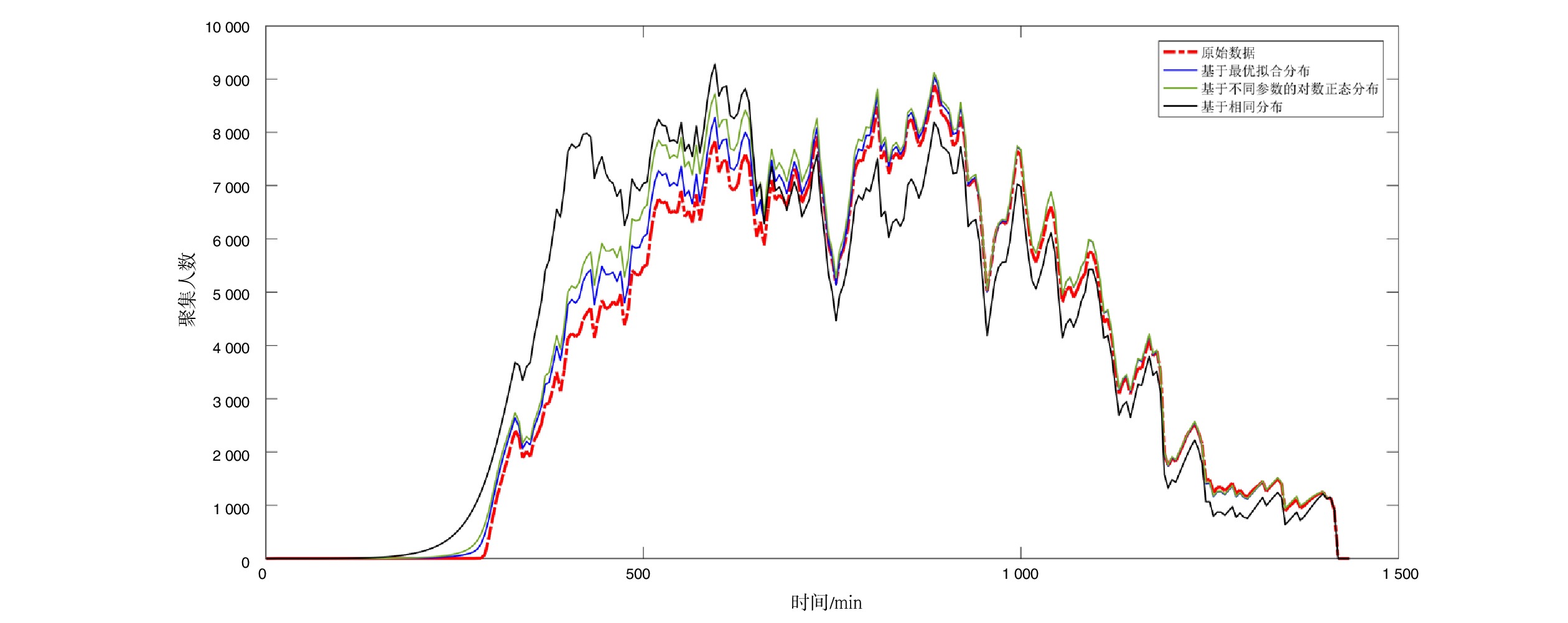
为更直观分析不同拟合方式下车站一天内的旅客聚集变化情况，绘制了不同拟合方式和实际车站旅客聚集人数对比图，如图5所示。
通过与原始数据对比可看出，3种拟合方式下基于最优拟合分布的计算结果更接近实际数据，能更准确地反应车站旅客最高聚集人数及其出现时间，为车站管理人员和相关工作人员合理安排组织工作提供更可靠依据。从整体趋势而言，基于最优拟合分布的计算方式在不同时刻的计算结果都较接近实际数据，且预测得到的车站全天最高聚集人数和实际数据出现时间一致，人数相近。因此，有必要分别拟合不同列车的旅客到站数据，以不同的最优拟合结果反应车站旅客聚集情况，从而更准确地计算车站旅客最高聚集人数。
3 结束语
本文分析了列车发车时间对旅客提前到站时长的影响，基于对数正态、复合负指数和威布尔3种分布对成都东站旅客聚集情况进行拟合分析，对比发现基于最优拟合分布的计算结果更接近实际车站旅客聚集数据，能够更准确地反应车站旅客最高聚集人数及其出现时间。揭示了对不同列车的旅客到站规律进行分别拟合的重要性，证明了后续研究不同列车旅客到站规律影响因素的必要性。
本文研究尚存在不足之处：（1）对旅客检票离开的处理相对简单，研究对象仅针对成都东站，未考虑不同车站、不同情况下检票闸机开放数量等因素；（2）仅在列车发车时间层面上对比了旅客提前到站时间的差异，后续可调研更多数据，从更多影响层面展开进一步研究。
-
表 1 D5178次列车拟合结果对比
指标 SSE R2 RMSE 对数正态 0.0013 0.9503 0.0046 威布尔 0.0021 0.9179 0.0059 复合负指数 0.0028 0.8879 0.0070 
下载: 导出CSV
-
[1] 国家铁路局. 铁路旅客车站设计规范: TB 10100—2018[S]. 北京: 中国铁道出版社, 2018. [2] 张天伟,罗玉屏,徐海锋. 铁路客运站最高聚集人数定义的分析 [J]. 中国铁路,2007(12):60-61,66. DOI: 10.3969/j.issn.1001-683X.2007.12.018 [3] 薛晓姣,杨宏志,任 楠. 应急条件下区域路网行程时间可靠性研究 [J]. 交通信息与安全,2019,37(2):25-32. DOI: 10.3963/j.issn.1674-4861.2019.02.004 [4] 姚加林,赵思源. 大型高铁车站最高聚集人数计算模型研究 [J]. 铁道科学与工程学报,2019,16(1):34-41. DOI: 10.19713/j.cnki.43-1423/u.T20210079 [5] 李建斌. 客运专线旅客最高聚集人数计算方法初探 [J]. 交通运输工程与信息学报,2007(1):9-13,33. DOI: 10.3969/j.issn.1672-4747.2007.01.003 [6] 张天伟,王明生,王希良. 设计期铁路客运站最高聚集人数预测模型研究 [J]. 铁道学报,2008(5):105-108. DOI: 10.3321/j.issn:1001-8360.2008.05.019 [7] 叶玉玲,李文卿. 高铁客运站最高聚集人数计算方法研究 [J]. 华东交通大学学报,2018,35(4):76-82. DOI: 10.16749/j.cnki.jecjtu.2018.04.011 [8] 刘启钢,朱克非,杜旭升. 大型客运站最高聚集人数仿真计算方法研究 [J]. 铁道学报,2011,33(8):1-6. DOI: 10.3969/j.issn.1001-8360.2011.08.001 [9] 陈喜春,王钰淇. 基于改进图解法的铁路客运站旅客集聚规律 [J]. 兰州交通大学学报,2015,34(4):90-94,106. DOI: 10.3969/j.issn.1001-4373.2015.04.017 [10] Oded Cats, Zafeira Gkioulou. Modeling the impacts of public transport reliability and travel information on passengers’ waiting-time uncertainty [J]. EURO Journal on Transportation and Logistics, 2017, 6(3): 247-270.
[11] Liu Xiaochen, Li Lingshan, Liu Xiaohua, et al. Field investigation on characteristics of passenger flow in a Chinese hub airport terminal [J]. Building and Environment, 2018(133): 51-61.
[12] 张天伟. 铁路客运站旅客聚集规律研究 [J]. 铁道学报,2009,31(1):31-34. [13] 张天伟,颜月霞,王 扬,等. 铁路特大型客运站候车室面积及数量计算模型研究 [J]. 铁道学报,2010,32(2):105-108. -
期刊类型引用(1)
1. 方鑫，刘通，程亚萍，孙宇铎，王菲儿. 基于GA-岭回归分析的机车车轮踏面磨耗量预测算法研究. 机车电传动. 2023(06): 71-78 . 
百度学术
其他类型引用(1)
计量
- 文章访问数: 231
- HTML全文浏览量: 62
- PDF下载量: 10
- 被引次数: 2
