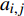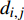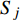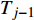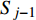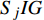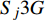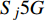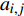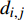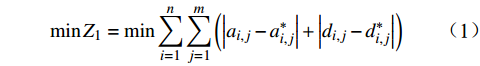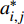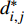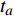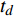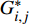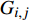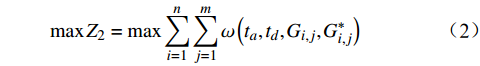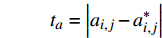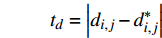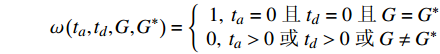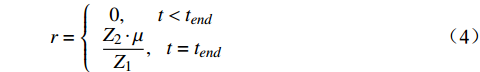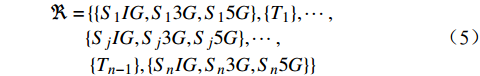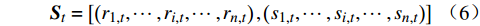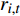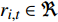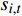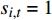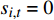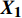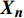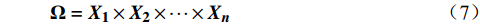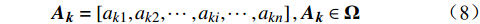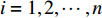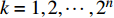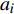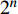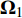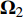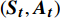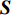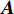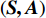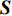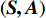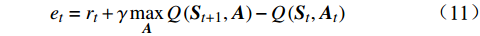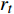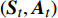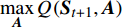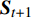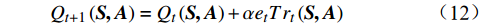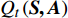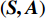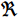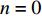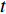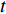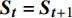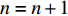Application of reinforcement learning algorithm in high speed railway operation scheduling
-
摘要: 随着我国高速铁路（简称：高铁）通达范围和行车密度的不断提高，运行计划调整日趋复杂，利用计算机和人工智能等技术手段辅助调度员制定阶段调整计划是高铁智能调度的发展趋势。高铁运行计划调整问题是一个多阶段决策问题，具有决策链长、规模大、约束多等特点，导致传统的强化学习方法Q学习算法的学习效率低、收敛缓慢。文章提出一种基于Q(λ)学习的高铁运行计划智能调整算法，采用累积式资格迹设计多步奖励更新机制，有效解决稀疏奖励下收敛慢的问题，目标函数设计中充分考虑了股道运用计划，更适合反应行车密度增大时到发线的使用情况。仿真实验表明，Q(λ)学习算法在学习效率、收敛速度和收敛结果上均优于传统的Q学习算法。Abstract: With the increasing access range and traffic density of China's high-speed railway, operation plan adjustment has become more complex. It is a development trend of intelligent dispatching of high-speed railway to use computer and artificial intelligence and other technical means to assist dispatchers in formulating phase adjustment plan. The adjustment of high-speed railway operation plan is a multi-stage decisions making problem, which is characterized by long decision chain, large scale and many constraints. As a result, the traditional reinforcement learning method Q-Learning algorithm has low learning efficiency and slow convergence. This paper proposed a Q(λ)-Learning based intelligent adjustment algorithm for high-speed railway operation plan, which used cumulative eligibility tracking to design a multi-step reward update mechanism, effectively solving the problem of slow convergence under sparse rewards. The track utilization scheme was fully considered in the design of the objective function, which was more suitable for coping with the use of arrival and departure lines when the traffic density increases. Simulation experiments showed that the proposed method was superior to the traditional Q-Learning algorithm in learning efficiency, convergence speed and convergence results.
-
目前，我国已建成世界上规模最大的高速铁路（简称：高铁）网。截至2020年底，我国高铁营业里程达3.79万km，占世界高铁总里程的69%[1]。随着列车开行数量的持续增长和通达范围的不断拓展，跨线运行列车增多，行车密度不断提高，运行计划调整日趋复杂，对高铁调度提出了更高的要求。现阶段的调度集中系统已在一定程度上降低了工作人员的劳动强度，实现了列车运行监视、到发点自动采集、调度命令网络下达等功能，但阶段计划的自动调整一般为顺延，只能处理简单的晚点情况，没有充分考虑更好的调整方案。因此，利用计算机优化和人工智能等技术手段为调度员提供辅助决策支持是智能高铁调度技术的一个发展方向。
由于传统的运筹学方法在求解调度问题时需要构建准确的数学模型。而高密度繁忙线路的行车约束条件复杂，有些约束条件（如股道运用约束等）难以采用等式或不等式构建准确的数学描述。因此，通常需要对模型和约束进行简化[2]，导致所求得的调度方案可行性偏低。但随着人工智能技术的发展，以强化学习为代表的多阶段决策优化算法可通过与环境的大量交互学习得到待求解问题的特征，并获得较优解。因此，采用强化学习方法的运行计划智能调整，可克服传统运筹学方法的建模难问题，通过与环境的交互，学习复杂的约束条件，获得具有较好可行性的高铁调度方案。因此，本文研究如何运用强化学习求解高铁调度问题，从而快速、准确地调整列车运行计划[3]。
近年来涌现出较多针对基于强化学习的列车调度方法的研究。文献[4]提出将强化学习方法的Q学习算法应用于高铁运行计划调整问题，并以3站2区间3车的小规模场景验证了Q学习算法在高铁运行计划调整问题中的可行性，但其实验场景较小，没有讨论决策链较长时学习效率、收敛速度和收敛结果不理想的问题；文献[5]将环境的状态定义为相对位置关系，相对关系的状态通过减小状态空间的规模来提高算法的收敛速度，但该状态包含的信息量过少，对环境的表征不够充分，影响了算法的收敛结果；文献[6]进一步研究了Q学习算法在高铁运行计划调整应用中的状态所包含环境元素对求解质量和收敛性的影响。上述文献使用的目标函数均较为简单，难以满足行车密度增加导致的复杂调度需求。
本文针对Q学习的学习过程奖励更新缓慢和简单目标函数无法反应到发线使用情况的问题，基于累积式资格迹，设计多步奖励更新机制，并在目标函数中引入股道运用计划，设计面向高铁运行计划调整的Q(λ)学习算法，其学习效率更高、收敛速度更快、收敛结果更好。
1 考虑股道运用约束的高铁运行计划调整问题
1.1 高铁运行计划调整问题描述
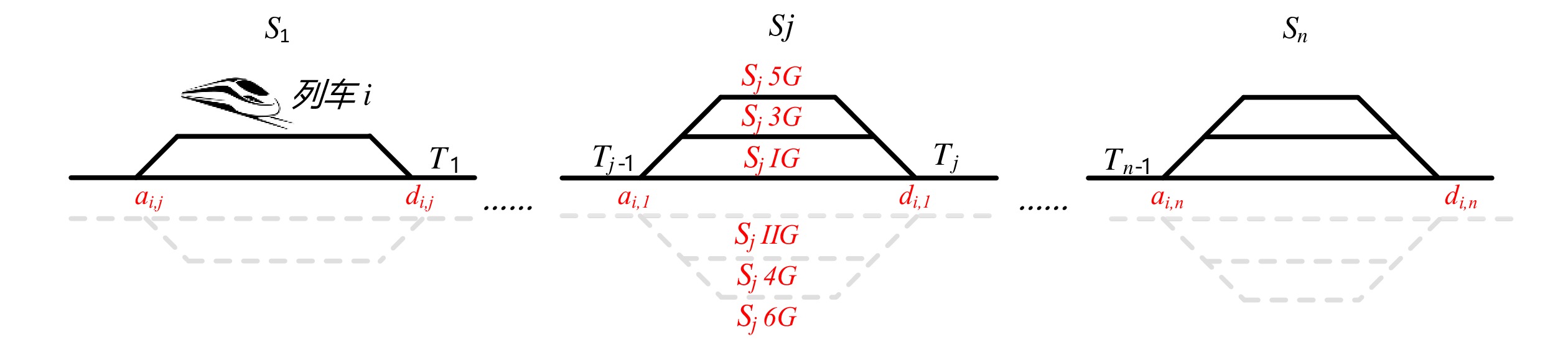
高铁运行计划调整问题是在一个时间区间内，固定已经发生的列车时刻点，对尚未发生的部分结合基本运输组织计划进行调整，包括调整列车的到发时间和车站使用的股道资源[7]。该问题涉及的到发时间和资源的定义如图1所示。
其中，
$ {a_{i,j}} $ 和$ {d_{i,j}} $ 分别为列车i在车站j的实际到达时间和发车时间；$ {S_j} $ 为第j个车站的车站名；$ {T_{j - 1}} $ 为车站$ {S_{j - 1}} $ 与$ {S_j} $ 之间的站间区间资源名；$ {S_j}IG $ 、$ {S_j}3G $ 、$ {S_j}5G $ 等为车站 j 的股道资源编号。 $ {a_{i,j}} $ 和$ {d_{i,j}} $ 即为高铁运行计划调整问题待求解的决策变量。1.2 高铁运行计划调整问题的目标函数设计
高铁运行计划调整问题通常采用的目标函数是最小化总晚点时间，则在给定时间区间下的n辆列车、m个车站的目标函数为
$$ \min {Z_1} = \min \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^m {\left( {\left| {{a_{i,j}} - a_{i,j}^*} \right| + \left| {{d_{i,j}} - d_{i,j}^*} \right|} \right)} } $$ (1) 其中，
$ a_{i,j}^* $ 和$ d_{i,j}^* $ 分别为列车i在车站j的图定到达时间和发车时间。随着高铁行车密度的日益增加，车站到发线使用率更高，使得列车群的约束日益复杂。如不按照股道运用计划安排行车，极易导致接发车进路重新排程，增加工作量和潜在安全风险，且需旅客临时更换乘车站台，影响服务质量。因此，单纯用总晚点时间作为目标函数，不能全面反映繁忙线路高密度行车下调度方案的性能优劣。综上，本文提出在目标函数中引入股道运用计划，以提高调度方案的实用性。
设
$ {t_a} $ 和$ {t_d} $ 为列车i在车站j的到达和发车时间的晚点量，$ G_{i,j}^* $ 为列车i在车站j使用的计划股道，$ {G_{i,j}} $ 为列车i在车站j使用的实际股道，是待求解的决策变量。考虑股道运用约束的高铁运行调整包括两方面：（1）列车使用的股道应与计划股道尽可能一致；（2）调度的到发时间与计划到发时间应尽可能一致。因此，引入股道运用计划的目标函数为$$ \max {Z_2} = \max \sum\limits_{i = 1}^n {\sum\limits_{j = 1}^m {\omega \left( {{t_a},{t_d},{G_{i,j}},G_{i,j}^*} \right)} } $$ (2) 其中：
$$ {t_a} = \left| {{a_{i,j}} - a_{i,j}^*} \right| $$ $$ {t_d} = \left| {{d_{i,j}} - d_{i,j}^*} \right| $$ $$ \omega \left( {{t_a},{t_d},G,{G^*}} \right) = \left\{ {\begin{array}{*{20}{c}} {1,{\text{ }}{t_a} = 0{\text{ }}且{\text{ }}{t_d} = 0{\text{ }}且{\text{ }}G = {G^*}} \\ {0,{\text{ }}{t_a} > 0{\text{ }}或{\text{ }}{t_d} > 0{\text{ }}或{\text{ }}G \ne {G^*}} \end{array}} \right. $$ 该目标函数尽可能保证列车群在到发时间和股道运用上与原计划一致，以实现在总晚点时间相差不大的情况下，优先选择临时变更到发线次数少的调度方案。通过引入该目标函数，可增大总晚点时间相差不大而股道运用不同的调度方案的差异性。
综上，将两部分目标函数合并，得到本文设计的综合目标函数为
$$ \min \frac{{{Z_1}}}{{{Z_2}}} $$ (3) 公式(3)的目标函数综合考虑了总晚点时间和股道运用计划，能够更好地反应调度方案能够恢复列车既定计划的程度，总晚点时间越小，股道运用计划重合度越高，则目标函数值越小，调度方案越好。
2 高铁运行计划调整中Q(λ)学习算法的应用
将传统的强化学习方法Q学习算法应用于决策链较长的高铁运行计划调整问题时，该算法的单步奖励更新机制会因过长的决策链导致学习过程奖励更新缓慢，需要更多的学习回合数，才能得到有效奖励值，影响算法的学习效率、收敛速度和收敛结果。本文提出的Q(λ)学习算法是在已有的Q学习算法基础上，通过优化奖励函数，设计启发式动作空间，增加累积式资格迹，以优化Q学习算法在高铁运行计划调整问题中的收敛速度和求解效果。
2.1 奖励函数的设计
在高铁运行计划调整问题中，一般要在所有列车终到或驶离本调度区段后，才能得到全面、准确的性能指标来评价一个调度方案的好坏。基于此种特点，本文将强化学习算法每个回合中间过程的奖励设为零[8]，将回合终止状态的奖励设为目标函数的倒数。结合公式（3）定义奖励函数为
$$ r = \left\{ {\begin{array}{*{20}{c}} {0,\;\;\;\;\;\;\;t < {t_{end}}} \\ {\dfrac{{{Z_2}\cdot \mu }}{{{Z_1}}},\;\;\;t = {t_{end}}} \end{array}} \right. $$ (4) 其中，μ为奖励的可调增益因子；t为决策链的决策时刻；tend为终止时刻，即所有列车都完成行驶的时刻。
2.2 状态和动作设计
2.2.1 高铁环境状态定义
在高铁运营中，铁路网的上下行是分开的，互不干扰，所以本文均以下行的环境为例进行说明。以图1为例，其下行资源集合的定义为
$$ \begin{aligned} \Re = & \left\{ \{ {{S_1}IG,{S_1}3G,{S_1}5G} \},\{ {{T_1}} \},\cdots , \right.\\ &\{ {{S_j}IG,{S_j}3G,{S_j}5G} \},\cdots , \\ &\left. {\{ {{T_{n - 1}}} \},\{ {{S_n}IG,{S_n}3G,{S_n}5G} \}} \right\} \end{aligned} $$ (5) 其中，奇数子集为某一车站的下行股道资源集合，每个元素均由车站名称和股道编号组成；偶数子集为某一站间区间资源的集合。
高铁调度环境的表现形式与决策时刻所有列车的位置及其下一资源的占用情况密切相关，因此，n辆列车的列车群在决策时刻t的状态为
$$ {{\boldsymbol{S}}_t} = \left[ {\left( {{r_{1,t}},\cdots ,{r_{i,t}},\cdots ,{r_{n,t}}} \right),\left( {{s_{1,t}},\cdots ,{s_{i,t}},\cdots ,{s_{n,t}}} \right)} \right] $$ (6) 其中，
$ {r_{i,t}} $ 为列车i在决策时刻t所处位置对应的资源，$ {r_{i,t}} \in \Re $ ；$ {s_{i,t}} $ 为列车i在t时刻的下一资源占用情况，$ {s_{i,t}=1} $ 表示未占用，${s_{i,t}=0} $ 表示已占用。2.2.2 智能体的动作定义
智能体是Q(λ)学习算法产生动作的映射。本文的智能体每次需要决策列车群的全部列车是否切换资源，将每辆列车的动作视作一个域
${\boldsymbol{X_i}} = \left( {0,1} \right)$ ，其中，1表示切换资源的动作，0表示保持资源不变的动作，n辆列车的动作域依次为${\boldsymbol{X_1}}$ 、${\boldsymbol{ X_2}}$ 、··· 、${\boldsymbol{X_n}}$ ，对应的动作空间为$$ {\boldsymbol{\Omega}} = {{\boldsymbol{X_1}}} \times {{\boldsymbol{X_2}}} \times \cdots \times {{\boldsymbol{X_n}}} $$ (7) 动作空间的每个动作向量是一个n元组，其通项为
$$ {\boldsymbol{A_k}} = \left[ {{a_{k1}},{a_{k2}},\cdots ,{a_{ki}},\cdots ,{a_{kn}}} \right],{\boldsymbol{A_k}} \in {\boldsymbol{\Omega}} $$ (8) 其中，
$ i = 1,2,\cdots ,n $ ，$ k = 1,2,\cdots ,{2^n} $ ；$ {a_i} $ 表示列车i的动作，其取值为0或1。公式（8）为n辆列车的原始动作空间 ，其维数是
$ {2^n} $ ，但其中大部分动作向量产生的调度方案较差，甚至无解。直接用其进行学习，会导致强化学习算法的学习效率低下、收敛缓慢。因此，需对动作空间进行预处理，通过启发式规则，预选出较好的动作向量。（1） 规则1：股道资源冲突
在列车进站时，如果当前列车的计划股道资源被占用，且当前车站不存在可临时调整的股道资源，则该列车不可切换资源。设
${{\boldsymbol{\Omega}} _1}$ 为目标列车在决策时刻t存在股道资源冲突的动作向量的集合。（2） 规则2：咽喉区段冲突
在切换资源时，如果多辆车同时驶入或驶离同一车站，则会在咽喉区段产生冲突。设
${{\boldsymbol{\Omega}} _2}$ 为目标列车在决策时刻t存在咽喉区段冲突的动作向量集合。将启发式规则1和规则2判断的不合理动作向量取并集，并与原始动作空间的全集取补集，即可得启发式动作空间为
$$ {{\boldsymbol{\Omega}} _{{s_t}}} = {C_{\boldsymbol{\Omega}} }\left( {{{\boldsymbol{\Omega}} _1} \cup {{\boldsymbol{\Omega}} _2}} \right) $$ (9) 2.3 基于累积式资格迹的经验更新机制
累积式资格迹[9]通过记录历史决策的状态—动作向量对
$\left( {{\boldsymbol{S_t}},{\boldsymbol{A_t}}} \right)$ 出现的次数和出现时间的远近，来反映智能体决策的倾向性和时效性。将已有的历史决策构成一张二维表，即累积式资格迹表，状态向量${\boldsymbol{S}}$ 为行索引，动作向量${\boldsymbol{A}}$ 为列索引，$\left( {\boldsymbol{S,A}} \right)$ 在表中对应的元素为信度值，其更新方式为$$ T{r_t}\left( {\boldsymbol{S,A}} \right) = \left\{ {\begin{array}{*{20}{c}} {\gamma \lambda T{r_{t - 1}}\left( {\boldsymbol{S,A}} \right),{\text{ }}\left( {\boldsymbol{S,A}} \right) \ne \left( {{{{{\boldsymbol{S}}_t}}},{{\boldsymbol{A}}_t}} \right)} \\ {\gamma \lambda T{r_{t - 1}}\left( {\boldsymbol{S,A}} \right) + 1,{\text{ }}\left( {\boldsymbol{S,A}} \right) = \left( {{{\boldsymbol{S}}_t},{{\boldsymbol{A}}_t}} \right)} \end{array}} \right. $$ (10) 其中，γ为奖励折扣因子；λ为资格迹衰减因子。在每个决策时刻t，都需要对完整的资格迹表进行更新。
累积式资格迹通过记录智能体历史决策的信息，来获取其决策的频度和逐新度，使智能体的决策信息更具全局性。
Q(λ)学习在高铁运行计划调整问题中利用环境评价性指标的反馈信号来优化状态值函数，该值函数为一张二维表，即Q表。其行索引为状态
${\boldsymbol{S}}$ ，列索引为动作${\boldsymbol{A}}$ ，元素值为某一$\left( {\boldsymbol{S,A}} \right)$ 对应的累积奖励。通过逐渐减小Q表的真实值与估计值之间的偏差，实现奖励最大化[10]，决策时刻t的偏差为$$ {e_t} = {r_t} + \gamma \mathop {\max }\limits_{\boldsymbol{A}} Q\left( {{{\boldsymbol{S}}_{t + 1}},{\boldsymbol{A}}} \right) - Q\left( {{{\boldsymbol{S}}_t},{{\boldsymbol{A}}_t}} \right) $$ (11) 其中，
$ {r_t} $ 为智能体与$\left( {{{\boldsymbol{S}}_t},{{\boldsymbol{A}}_t}} \right)$ 所对应的即时奖励；$\mathop {\max }\limits_{\boldsymbol{A}} Q\left( {{{\boldsymbol{S}}_{t + 1}},{\boldsymbol{A}}} \right)$ 为t时刻后继状态向量${{\boldsymbol{S}}_{t + 1}}$ 在Q表对应行的最大Q值。累积式资格迹Q值的更新方式为$$ {Q_{t + 1}}\left( {\boldsymbol{S,A }}\right) = {Q_t}\left( {\boldsymbol{S,A}} \right) + \alpha {e_t}T{r_t}\left( {\boldsymbol{S,A}} \right) $$ (12) 其中，
${Q_t}\left( {\boldsymbol{S,A}} \right)$ 为t时刻$\left( {\boldsymbol{S,A}} \right)$ 对应的Q值；α为学习率。不同于采用单步更新策略的Q学习，Q(λ)学习通过引入累积式资格迹进行回溯，实现多步更新，有效解决因决策链较长导致的学习过程奖励更新缓慢问题，提高了学习效率和收敛速度。
3 算法实现
综上所述，本文设计的面向高铁运行计划智能调整的Q(λ)学习算法的基本流程如图2所示。
（1）初始化Q(λ)学习的基本参数：最大迭代次数N、α、γ、λ、值函数表Q、资格迹表Tr、计划时刻表T和资源列表
$\Re $ 。加载高铁交互环境的数据：事件队列、状态列表等。（2）由晚点事件获取其对应的状态向量S0，初始化Q表、资格迹表Tr和当前回合数
$ n=0 $ 。（3）每个回合开始前，将Tr清零。
（4）获取决策时刻
$ t $ 的状态 St，再根据经典的动作选择策略（ε贪婪策略）在由公式（9）生成的启发式动作空间中选择动作At，该动作控制高铁交互环境的列车运行，进而产生后继状态St+1。 （5）由公式（4）得到的奖励值，根据公式（11）计算
$ t $ 时刻的偏差，根据公式（10）更新Tr的信度值，再根据公式（12）更新Q表的Q值，随后更新当前状态${{\boldsymbol{S_t}}} = {{\boldsymbol{S}}_{{\boldsymbol{t}} + 1}}$ 。（6）判断St是否为终止状态，即所有列车是否完成行驶。如果没有完成行驶，则返回（4），否则执行下一步。
（7）更新当前回合数
$ n=n+1 $ ，判断其是否大于最大迭代次数。如果不大于，则返回（3），否则完成学习，输出得到的高铁运行计划调整方案。4 试验分析
4.1 仿真案例
本文选取京沪（北京—上海）铁路繁忙区段的济南西站—蚌埠南站在11:00~16:00时段的下行列车群作为实验案例，其间各站的站场规模如表1所示。
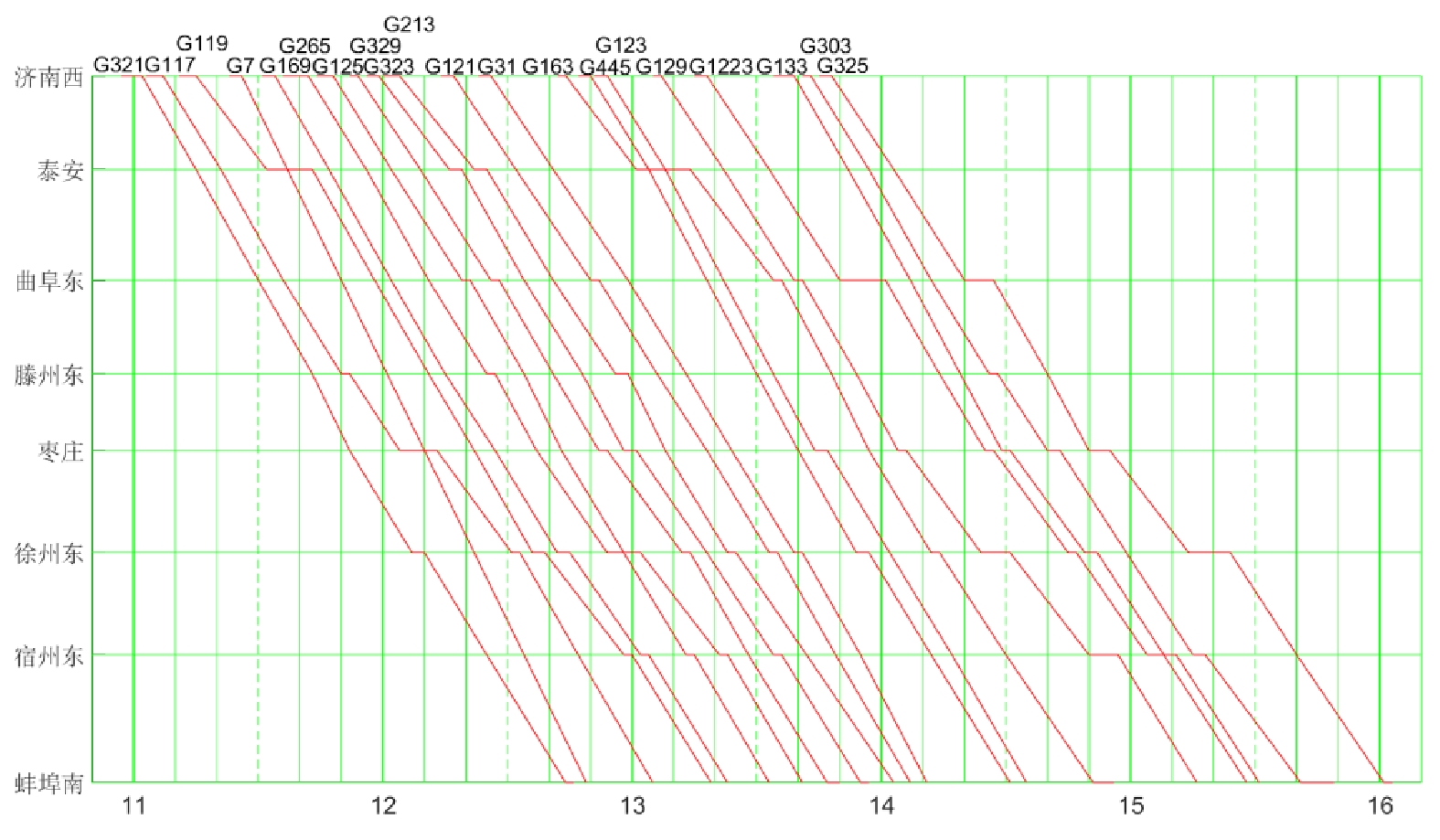
表 1 京沪线济南西到蚌埠南站场规模表火车站名 站场规模 下行到发线的站场规模 正线 侧线 济南西 9台18线 1 8 泰安 2台6线 1 2 曲阜东 2台6线 1 2 滕州东 2台4线 1 1 枣庄 2台6线 1 2 徐州东 7台15线 1 7 宿州东 2台6线 1 2 蚌埠南 5台11线 1 4 试验案例使用的时刻表基于京沪铁路的真实运营案例，8站、7区间、20辆列车，共320个到发时间点，计划运行图如图3所示。
4.2 算法性能对比实验
基于4.1节济南西站—蚌埠南站的高铁调度环境，分别使用Q学习和Q(λ)学习算法对列车突发晚点情况进行调度。Q学习算法的基本参数为α=0.3，γ=0.8，μ=100，N=700；Q(λ) 学习算法的基本参数为α=0.3，γ=0.7， λ=0.8，μ=100，N=700。列车群的突发晚点设置为G321在济南西站晚到5 min，G117在泰安站晚到12 min。
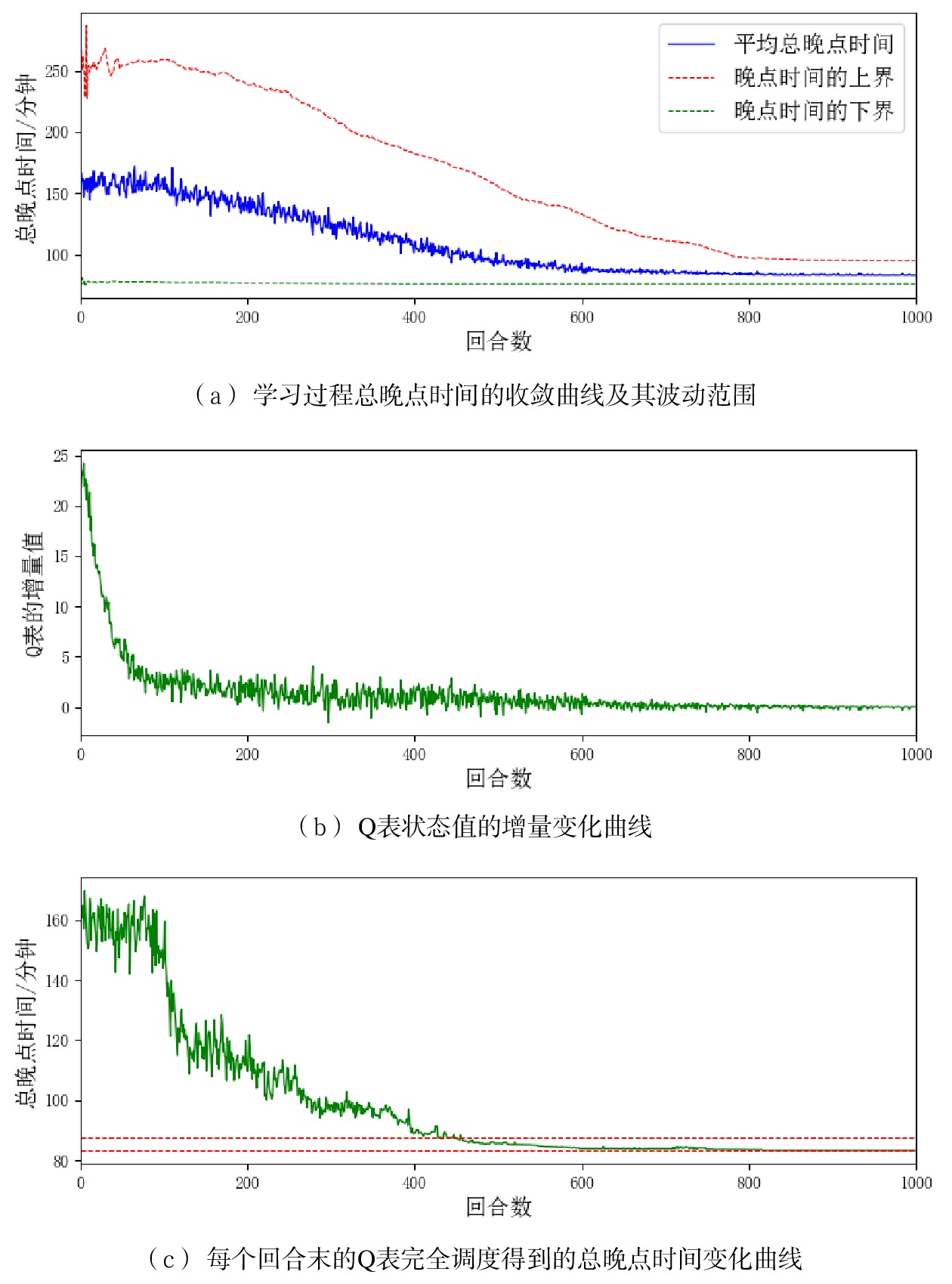
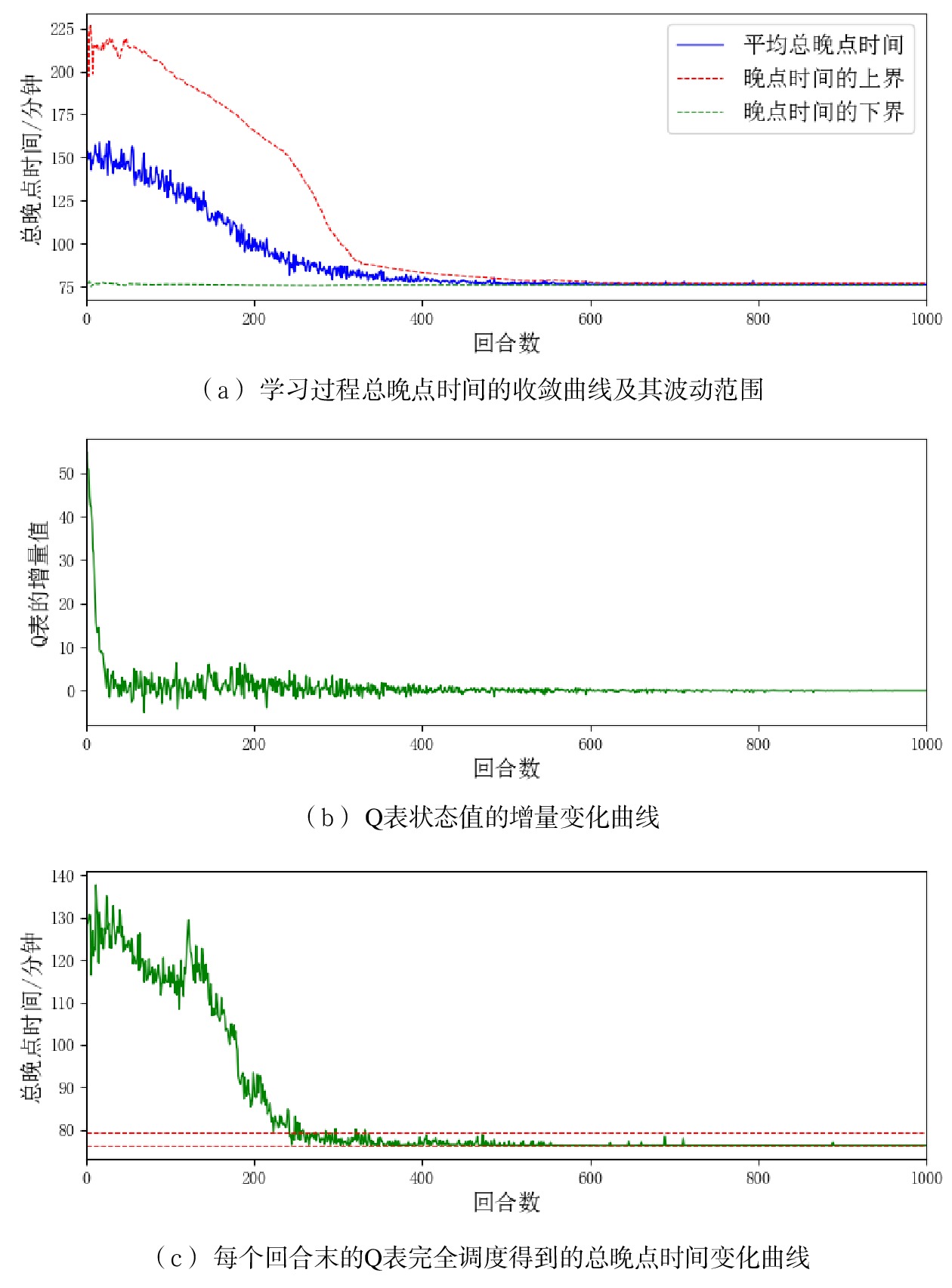
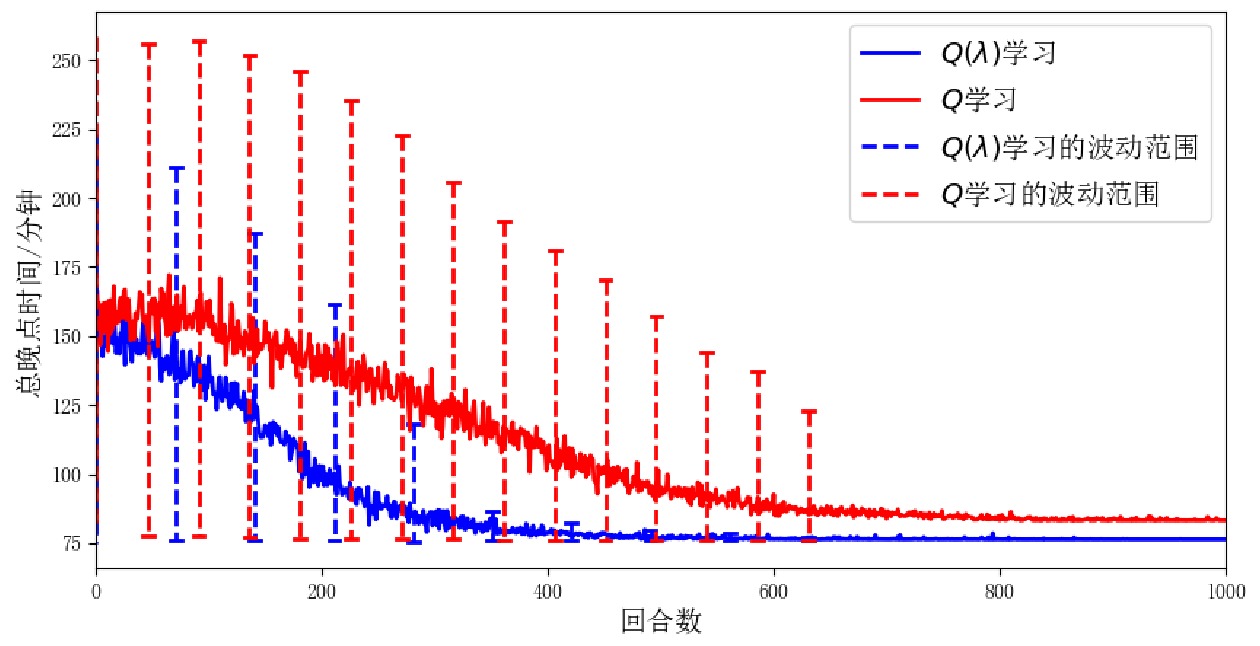
使用上述设置采用不同的随机数种子进行100次独立实验，2个算法的学习过程如图4和图5所示，对比结果如图6所示。
图6中，Q(λ)学习的收敛曲线始终位于Q学习收敛曲线的下方，表明在相同的回合处，Q(λ)学习具有更好的学习效果；Q(λ) 学习400回合时已收敛到较好的调度方案，总晚点时间78 min，而Q学习700回合时的调度方案总晚点时间仍为85 min，这表明Q学习在有限的学习次数下未能收敛到较好结果。在图5（b）和图4（b）中，Q(λ)学习和Q学习的Q表增量分别在400和600回合处开始趋近于0，这表明前者的Q表能够更快的收敛；在图5（c）和图4（c）中，Q(λ)学习和Q学习完全调度达到各自最优结果的5%误差范围内的起始位置分别是255和450回合处，也表明前者的收敛速度更快，学习效率更高。综上，Q(λ)学习算法在学习效率、收敛速度和收敛结果上均优于传统的强化学习方法Q学习算法。
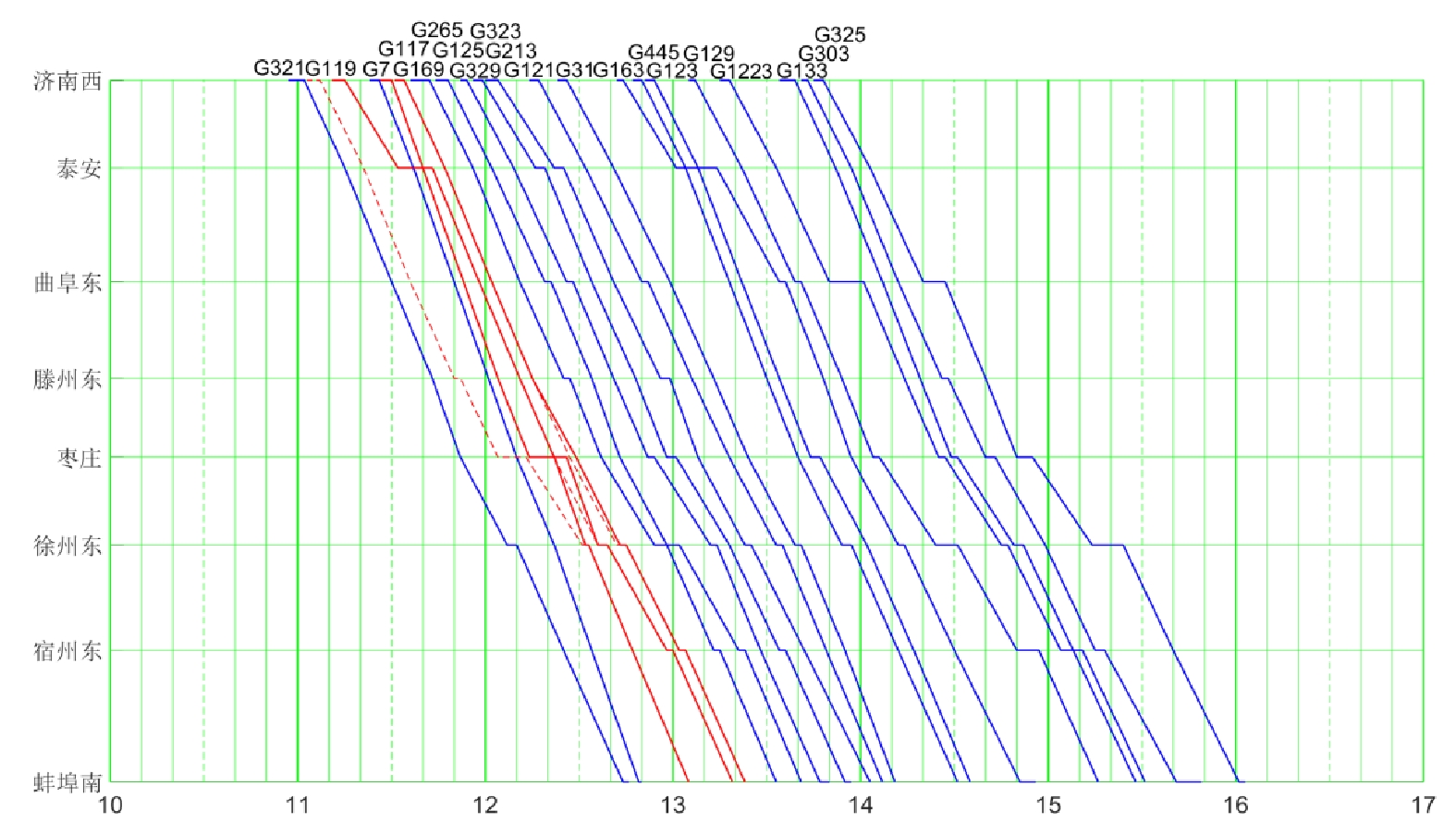
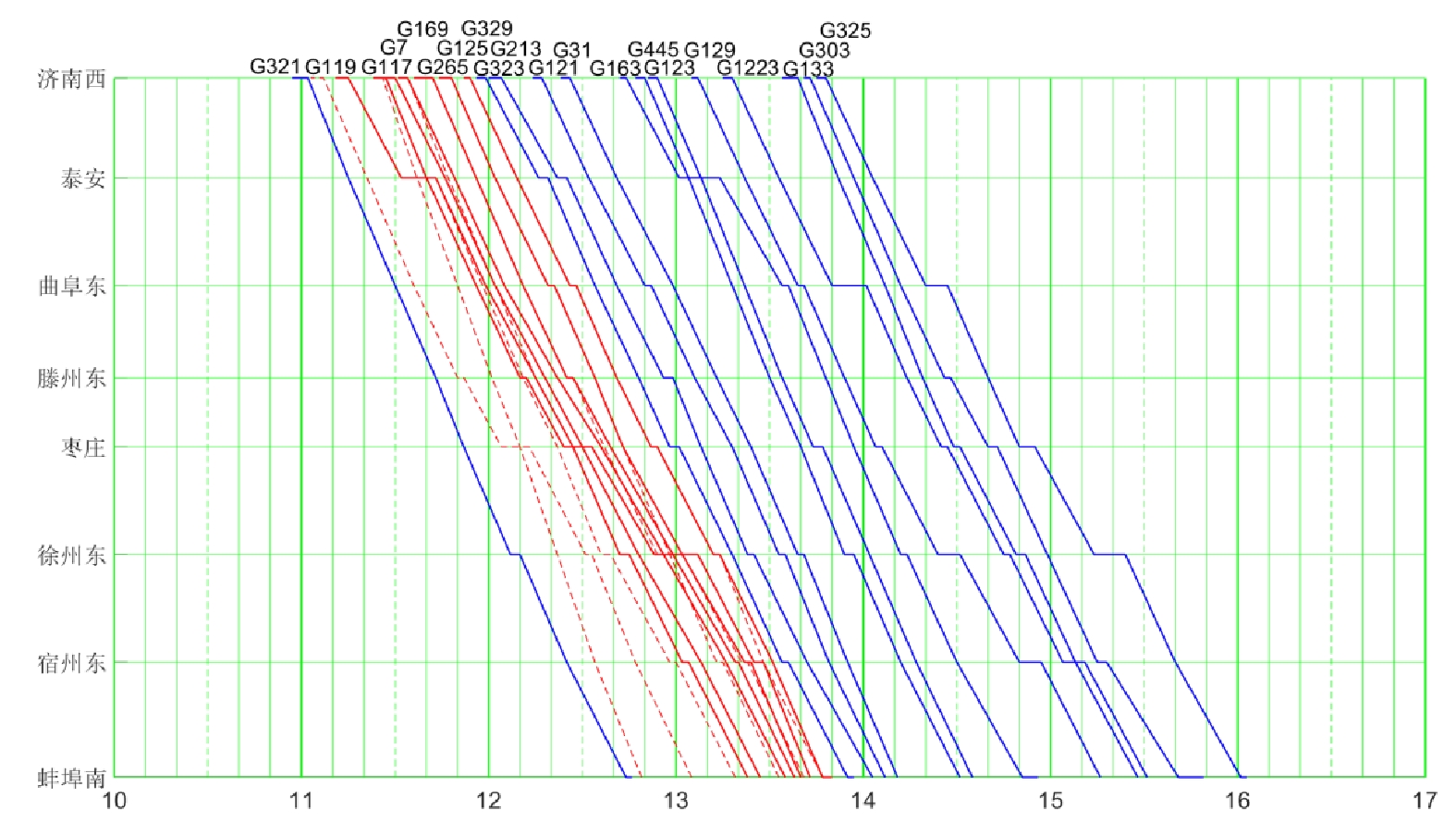
先来先服务（FCFS，First Come First Service）的调度策略与调度员进行运行计划调整的过程十分相似，因此，本文用FCFS的调整结果近似人工调度的结果，设置列车G117在济南西站晚点20 min，分别用Q(λ)学习算法和FCFS进行运行计划调整，运行计划调整方案如图7、图8所示。
图8中，基于FCFS的调度策略，G117晚点20 min，早于G7，所以先服务G117，迫使其紧邻的列车向后顺延，产生横向和纵向的晚点传播，在满足高铁行车安全的前提下，最终得到的调整方案影响了7辆列车在7个区间约60 min的行驶。而图7中，由于Q(λ)学习能充分利用已有经验，让G117再晚3 min发车，先服务G7，使G7和G169没有受到干扰，即没有产生列车运行干扰的横向传播，接着G169在枣庄站受到G119的影响，晚到1 min，在下一站又恢复原计划，最终得到的调整方案只影响了1辆列车在5个区间和2辆列车在2个区间的行驶，快速恢复了图定计划。综上，在行车密度较大的复杂场景中，Q(λ)学习能够得到比FCFS更好地运行调整方案，能够更好的辅助调度员快速、安全地完成高铁列车的运行计划调整。
5 结束语
为应对高铁行车密度日益增大使简单的目标函数不能较好反应调度方案在密集列车群下车站股道的分配和使用的情况，本文通过在目标函数中引入股道运用计划使调度过程更加可靠和严谨，同时，突出运行计划调整方案的差异性。并针对高铁运行调整时由于决策链过长造成的学习过程奖励更新缓慢问题，基于累积式资格迹设计多步奖励更新机制，使单步决策更具全局性。基于京沪铁路济南西站—蚌埠南站的线路数据和运营数据进行突发晚点下运行计划调整对比实验，结果表明，在相同的学习回合数下，本文设计的面向高铁运行计划调整的Q(λ)学习算法，在学习效率、收敛速度和收敛结果上均优于传统的强化学习方法Q学习算法。但目前，本文只对单一区段进行实验，尚未考虑多区段铁路网的复杂场景，将在今后的工作中继续改进。
-
表 1 京沪线济南西到蚌埠南站场规模表
火车站名 站场规模 下行到发线的站场规模 正线 侧线 济南西 9台18线 1 8 泰安 2台6线 1 2 曲阜东 2台6线 1 2 滕州东 2台4线 1 1 枣庄 2台6线 1 2 徐州东 7台15线 1 7 宿州东 2台6线 1 2 蚌埠南 5台11线 1 4 
下载: 导出CSV
-
[1] 陈 珺,苗 茁. 高铁晚点列车智能调度系统的研究与开发 [J]. 铁路计算机应用,2021,30(2):5-9. [2] 邓 念,彭其渊,占曙光. 干扰条件下高速铁路列车运行实时调整问题研究 [J]. 交通运输系统工程与信息,2017,17(4):118-123. [3] 占曙光,赵 军,彭其渊. 高速铁路区间能力部分失效情况下列车运行实时调整研究 [J]. 铁道学报,2016,38(10):1-13. DOI: 10.3969/j.issn.1001-8360.2016.10.001 [4] D. Šemrov, R. Marsetič, M. Žura, et al. Reinforcement learning approach for train rescheduling on a single-track railway [J]. Transportation Research Part B, 2016: 86.
[5] Khadilkar H. A Scalable Reinforcement Learning Algorithm for Scheduling Railway Lines [J]. IEEE Transactions on Intelligent Transportation Systems, 2019, 20(2): 727-736. DOI: 10.1109/TITS.2018.2829165
[6] Zhu Y, Wang H, Goverde R. Reinforcement Learning in Railway Timetable Rescheduling[C]// The 23rd IEEE International Conference on Intelligent Transportation Systems (IEEE ITSC 2020). Rhodes, Greece: IEEE, 2020.
[7] 张英贵,雷定猷,汤 波,等. 铁路客运站股道运用窗时排序模型与算法 [J]. 铁道学报,2011,33(1):1-7. DOI: 10.3969/j.issn.1001-8360.2011.01.001 [8] 韩忻辰,俞胜平,袁志明,等. 基于Q-learning的高速铁路列车动态调度方法 [J]. 控制理论与应用,2021,38(10):1511-1521. DOI: 10.7641/CTA.2021.00612 [9] Jing Peng, Ronald J. Williams. Incremental Multi-Step Q-Learning [J]. Machine Learning, 1996(22): 1-3.
[10] 王渝红,胡胜杰,宋雨妍,等. 基于强化学习理论的输电网扩展规划方法 [J]. 电网技术,2021,45(7):2829-2838. -
期刊类型引用(2)
1. 沙淼，张可心，刘志刚，邱瑞昌，陈杰. 基于目标速度追踪的城轨列车节能优化算法. 都市快轨交通. 2023(06): 40-48 . 
百度学术
2. 马阳阳，孟学雷，贾宝通，任媛媛，秦永胜. 基于列车运行时间偏差惩罚的高速列车节能优化方法. 交通信息与安全. 2021(04): 84-91 . 百度学术
其他类型引用(13)
计量
- 文章访问数: 209
- HTML全文浏览量: 182
- PDF下载量: 56
- 被引次数: 15
