Design of railway monitoring and early warning system based on Beidou third Generation
-
摘要: 针对铁路安全隐患问题，提出将第三代北斗卫星导航系统（简称：北斗三代）高精度定位技术引入铁路监测预警，设计了基于北斗三代的铁路监测预警系统，该系统利用北斗高精度定位的原理实现位移数据高精度监测，同时具备实时传输和即时预警等功能。实践证明，该系统相对于基于GPS的监测预警系统具有明显优势，可见的卫星个数显著增加，水平精度提高20%以上，高程精度提高50%以上。同时通过不同基线长度下监测性能的对比，为合理布设基准站提供参考。
-
关键词:
- 第三代北斗卫星导航系统 /
- 高精度定位 /
- 铁路 /
- 监测预警 /
- 基准站
Abstract: Aiming at the hidden danger of railway safety, this paper introduced the third generation Beidou satellite navigation system (Beidou third generation for short) high-precision positioning technology into railway monitoring and early warning, designed the railway monitoring and early warning system based on Beidou third Generation. The system used the principle of Beidou high-precision positioning to implement high-precision monitoring of displacement data, and had real-time transmission and instant warning functions. Practice has proved that the system has obvious advantages over the GPS based monitoring and early warning system, with a significant increase in the number of visible satellites, an increase in horizontal accuracy of more than 20%, and an increase in elevation accuracy of more than 50%. Through the comparison of monitoring performance under different baseline lengths, it provides a reference for the reasonable deployment of reference stations. -
对于铁路的安全运营来说，任何微小的异常或干扰都有可能导致严重的安全事故，造成经济损失甚至人员伤亡。铁路轨道的沿线边坡和路基因受到雨雪、地质运动等因素的影响而存在滑坡、崩塌、沉降等安全隐患。以边坡为例，岩体在重力、构造力、地震力，以及各种外营力的长期作用下，会有一种向下滑落的趋势，这种趋势受到岩体本身抗剪切、抗破坏力的阻抗。当岩体阻抗力小于向下滑落的破坏力时，岩体滑坡或崩塌的情况就会发生，并极有可能会造成灾害。除了地质风险外，路基、桥梁、隧道、车站等铁路基础设施的状况也影响着铁路的运营安全。
由于北斗卫星导航系统（简称：北斗）在变形监测方面的作用日益凸显[1-2]，很多专家和学者已经开始将北斗应用于铁路安全监测领域[3-5]。秦健等人[6]深入探讨了北斗地基增强系统构建和基准站选址问题，但尚未涉及第三代北斗卫星导航系统（简称：北斗三代）的变形监测。
本文基于北斗三代高精度定位技术，设计铁路监测预警系统，详细阐述北斗三代的变形监测原理；同时，利用实际数据对北斗相较于全球定位系统（GPS，Global Positioning System）的优势进行计算和论证，对比不同基线长度对变形监测精度的影响，为基准站的布设距离提供参考。
1 基于北斗三代的铁路监测预警系统架构
基于北斗三代的铁路监测预警系统以北斗三代接收机为核心，融合位移、雨量、水位等全维度感知信息，能够实时且动态地测量监测点的要素变化，通过高通量、自适应、多回路的通信网络将监测数据全天候、不间断地回传至监测云平台。监测云平台对回传的监测数据进行计算和分析，根据结果发出预警信息，保障铁路的安全运营。
1.1 以北斗为核心的实时感知网络
1.1.1 北斗区域增强系统
北斗区域增强系统为服务区域内提供永久性、连续运行的差分信息，避免同一区域内基准站的重复建设，提高设备的利用率。
北斗区域增强系统由连续运行的基准站网、控制与数据中心、高速数据通信网、运营服务等子系统组成。各子系统主要功能及其构成，如表1所示。
表 1 各子系统的功能及其构成子系统名称 功能 构成 基准站网 负责卫星定位数据和大气数据的采集、接收、传输；
负责设备完好性的监测北斗接收机；
电源；
网络设备；
避雷设备；
气象监测设备控制与数据中心 负责参考站信息管理；
系统管理与维护；
数据分流与处理；
信息编码与解码数据处理服务器组；
网络设备；
数据收发设备；
电源保障设备高速数据通信网 负责各子系统数据的传输 有线通信；
蜂窝网络；
天基通信运营服务 负责用户管理与鉴权；
监测用户定位状态；
将生成的差分数据产品播发至监测站运营服务器组；
运营软件1.1.2 多维度实时感知网络
多维度实时感知网络的主要功能是针对灾害隐患点建设全维度地质灾害诱发因素（如灾害体位移、气象环境、水位、含水量等）监测网络，由全维度监测传感设备组成。多维度实时感知网络通过这些传感设备采集影响或诱发地质灾害的可量化信息，为灾害监测、风险评估、地灾预警、应急管理等提供数据依据。多维度实时感知网络的典型配置如表2所示。
表 2 多维度实时感知网络的典型配置感知设备 配置的设备数量/套 高精度北斗三代监测站 9 雨量计 1 深部位移计 3 土壤含水量传感器 3 孔隙水压计 2 视频监控设备 1 声光报警器 1 表2所列配置能够监测造成滑坡灾害的相关因素。各感知设备的作用如下。
（1）高精度北斗三代监测站
高精度北斗三代监测站是核心设备，由北斗三代接收机、结构件、供电设备构成，提供高精度三维位移信息。
（2）雨量计
降雨是诱发滑坡灾害的主要因素，降雨量是滑坡灾害监测中必要的监测因素。多维度实时感知网络能够通过隐患点区域设置的雨量计，实时采集隐患点的小时降雨量信息，实现对滑坡灾害的预警。
（3）深部位移计
深部位移监测通过打孔方式在灾害体深层不同深度安装深部位移监测设备，采集灾害体深层的倾斜及相对位移变化，从而获得地质内部结构变化情况，为灾害体发展及变化趋势提供多维度的监测数据。深部位移计是监测滑坡灾害诱发因素的重要手段。
（4）土壤含水量传感器
土壤含水量的变化可导致土体自重、土体粘接力和内摩擦角的变化，从而使土体内部力学平衡结构产生变化。土壤含水量是发生滑坡灾害的重要因素，因此，多维度实时感知网络通过土壤含水量传感器监测土体中多层次的水分含量变化，对土体内部的平衡结构进行监测。
（5）孔隙水压计
孔隙水压力增大易引起感知体失稳。监测孔隙水压力，不间断地感知灾害体在土体固结、基础变形、水流渗透等因素作用下孔隙水压力的大小和变化，能够为多维度实时感知网络分析灾害体的稳定性提供物理数据依据。
（6）视频监控设备
视频监控作为常见的可视化监测手段，可以直观地观察被监测灾害体的变化情况。此外，具有夜视功能的视频设备可以实现对灾害体24 h不间断监测。同时，远程云台控制功能可以使监测人员通过远程控制的方式全面了解灾害体周边情况。
（7）声光报警器
声光报警器能够进行声音告警及光电告警，快速且直接地提醒灾害体周边的群众。
1.2 高通量自适应多回路通信网络
为了保证监测数据能够不间断实时回传至云平台，铁路监测预警系统设计了多回路通信链路，由蜂窝移动通信网、窄带物联通信网及天基卫星网组成。当蜂窝移动网和窄带物联通信网受到灾害影响且通信中断时，通信可以切换至天基卫星网，这是因为卫星通信不受地域限制，不受灾害影响，且支持灵活部署。
铁路监测预警系统使用的宽带卫星一体化设备为Ka波段终端，该终端可直接提供RJ45接口，方便其他设备接入。宽带一体化设备如图1所示。
1.3 云平台
铁路监测预警系统通过监测云平台，依托高吞吐量数据处理技术、并行业务集群计算技术，实现快速评估地质灾害隐患点的风险，并提供相应的预警预报及辅助决策信息，建立地质灾害隐患点的全面防控体系，实现地质灾害可控制、可预防。
云平台能够对所有监测数据进行清洗、分析、汇集、存储和管理，并基于云计算技术对监测数据进行分布式大数据分析及处理，得到所有监测对象的全维度监测信息。云平台监测的北斗位移情况如图2所示。
铁路监测预警系统通过云平台集成的大数据分析和处理模块进行数据处理和可视化展示。当异常情况发生时，铁路监测预警系统将通过现场广播、电话、短信、邮件等形式实时向管理机构汇报预警信息，并提供高精度实时应急管理支持。
2 北斗变形监测技术
2.1 双差相对定位
北斗定位的误差源主要包括星历误差、卫星钟差、接收机钟差、电离层时延、对流层时延等因素，这些误差源产生的影响可以通过双差相对定位进行消除。在一定距离内，同步观测的北斗接收机之间存在误差相关性，通过观测值之间组差，可使误差被消除或大幅削弱，得到较高精度的相对位置。
监测站接收机
$ j $ 与卫星$ q $ 的载波相位观测方程[7]为$$ \lambda \varPhi _j^q = \rho _j^q - \lambda N_j^q + c\delta {t_j} - c\delta {t^q} - ({d_I})_j^q + ({d_T})_j^q + {e_\varPhi } $$ (1) 其中，
$ \lambda $ 为波长；$\varPhi _j^q$ 为接收机$ j $ 与卫星$ q $ 的载波相位观测值；$ N_j^q $ 为接收机$ j $ 与卫星$ q $ 的整周模糊度；$ \delta {t_j} $ 为接收机钟差；$ c $ 为光速；$ {d_I} $ 为电离层时延误差；$ {d_T} $ 为对流层时延误差；$e_{\Phi}$ 为观测噪声。若于基准站接收机
$ i $ 对卫星$ q $ 进行同步观测，可得观测方程为$$ \lambda \varPhi _i^q = \rho _i^q - \lambda N_i^q + c\delta {t_i} - c\delta {t^q} - ({d_I})_i^q + ({d_T})_i^q + e_{\varPhi ,j}^q $$ (2) 两个监测站间观测方程组差，可得站间单差观测方程为
$$ \lambda \Delta \varPhi _{ij}^q = \rho _j^q - \rho _i^q - \lambda \Delta N_{ij}^q + c\Delta \delta {t_{ij}} - \Delta {d_I} + \Delta {d_T} + \Delta e_{\varPhi ,ij}^q $$ (3) 其中，
$ {{\Delta }} $ 为站间差算子，$ \lambda \Delta \varPhi _{ij}^q = \lambda \varPhi _j^q - \lambda \varPhi _i^q $ ，同理有$ \lambda \Delta N_{ij}^q = \lambda \Delta N_j^q - \lambda \Delta N_i^q $ 。通过站间观测方程组差，单差观测方程消除了卫星钟差，并且削弱了大气时延（电离层和对流层时延）误差的影响。基准站接收机$ i $ 可来自实体基准站，也可来自增强系统计算的虚拟参考站。两个监测站同时对卫星
$ p $ 也能得到单差观测方程，在不同卫星$ p $ 、$ q $ 间观测方程组差，可得站星双差观测方程为$$ \begin{aligned} &\lambda \nabla \Delta \varPhi _{ij}^{pq} = \rho _j^q - \rho _i^q - \rho _j^p + \rho _i^p - \lambda \nabla \Delta N_{ij}^{pq} - \nabla \Delta {d_I} +\\ &\;\;\;\;\;\;\;\;\;\;\qquad\nabla \Delta {d_I} + \nabla \Delta e_{\varPhi ,ij}^{pq} \end{aligned}$$ (4) 其中，
$ \nabla $ 为星间差算子；$ \nabla \Delta $ 为站星双差，$ \lambda \nabla \Delta \varPhi _{ij}^{pq} = \lambda \Delta \varPhi _{ij}^q - \lambda \Delta \varPhi _{ij}^p $ ；$ \nabla \Delta N_{ij}^{pq} $ 中的站星双差符号含义同理。双差方程消除了接收机钟差项，并进一步削弱了大气时延误差的影响。残余大气时延误差的大小取决于基准站和监测站之间的距离，距离越近，误差越小。解算双差观测方程时，基准站接收机 i 坐标由其他渠道获得，对观测方程中的
$\rho _j^q $ 和$\rho _j^q $ 线性化，则有$\rho _j^q = $ $ \rho _{j0}^q + [ - l_j^q\;\; - m_j^q\;\; - n_j^q]d{\bf{X}} $ ，$\rho _j^p = \rho _{j0}^p + [ - l_j^p\;\; - m_j^p\;\; - n_j^p]d{\bf{X}} $ ，$\rho _{j0}^q $ 和$\rho _{j0}^p $ 为坐标近似值${{\bf{X}}_0} = {\left[ {\begin{array}{*{20}{c}}{{x_0}}&{{y_0}}&{{z_0}}\end{array}} \right]^{\rm{T}}} $ 计算的几何距离，$l_j^q $ 、$m_j^q $ 、$n_j^q $ 为接收机到卫星的方向余弦，$d{\boldsymbol{X}} $ 为所求位置改正数向量参数。忽略大气折射延迟误差影响，略去
$\nabla \Delta e_{\Phi ,ij}^{pq}$ 的索引标记，得线性化后的双差载波观测方程为$$ \begin{array}{l} \lambda \nabla \Delta \Phi _{ij}^{pq} = [ - (l_j^q - l_j^p)\;\;\; - (m_j^q - m_j^p)\;\;\; - (n_j^q - n_j^p)]d{\bf{X}} -\\ \;\;\;\;\;\;\;\lambda \nabla \Delta N_{ij}^{pq} + \nabla \Delta \rho _{ij0}^{pq} + \nabla \Delta {e_\Phi } \end{array}$$ (5) 其中，
$\nabla \Delta \rho _{ij0}^{pq} = \rho _{j0}^q - \rho _i^q - \rho _{j0}^p + \rho _i^p $ 。将方向余弦表示为更简洁的向量形式，则有
$$ \lambda \nabla \Delta \Phi _{ij}^{pq} - \nabla \Delta \rho _{ij0}^{pq} = - ({\bf{l}}_j^q - {\bf{l}}_j^p) \cdot d{\bf{X}} - \lambda \nabla \Delta N_{ij}^{pq} + \nabla \Delta {e_\Phi }$$ (6) 将所有共视卫星双差观测方程联立，构成矩阵形式的双差观测方程组
$$ {\boldsymbol{L}} = {\boldsymbol{A}}\left[ {\begin{array}{*{20}{c}} {\boldsymbol{X}}\\ {\boldsymbol{N}} \end{array}} \right] + {\boldsymbol{e}}$$ (7) 其中，X代指dX，整周模糊度向量N由
$\nabla \Delta N_{ij}^{pq} $ 构成，A为观测系数矩阵，e 为观测噪声向量。解方程组可得位置浮点解和模糊度浮点解。
要得到毫米级位置测量结果，必须对浮点解进行固定，将整周模糊度参数恢复为整数。模糊度搜索实质是求解整数最小二乘估计值，而最小二乘模糊度降相关平差（LAMBDA，Least Square AMBiguity Decorrelation Adjustmen）方法目前体系完整、应用广泛，能够对原始模糊度进行整数变换，降低模糊度之间的相关性，缩小搜索范围。
将混合整数最小二乘估计转化为整数最小二乘估计问题[8]，如式（8）所示。
$$ \mathop {\min }\limits_N {\left( {{\boldsymbol{\hat N}} - {\boldsymbol{N}}} \right)^{\rm{T}}}{\boldsymbol{Q}}_{{\boldsymbol{\hat N}}}^{ - 1}\left( {{\boldsymbol{\hat N}} - {\boldsymbol{N}}} \right)\;\;\;\;\;\;{\boldsymbol{N}} \in {\rm{Z}} $$ (8) 其中，
${\boldsymbol{Q}}_{{\boldsymbol{\hat N}}}^{} $ 为整周模糊度向量估值协方差矩阵。基于LAMBDA方法搜索确定整周模糊度固定解
${\overset{\smile} {\boldsymbol{N}}}$ ，回代得到坐标参数的固定解${\overset{\smile} {\boldsymbol{X}}}$ 及代表其误差特性的协方差矩阵${{{{\boldsymbol{Q}}}}_{\overset{\smile} {\boldsymbol{X}}}}$ ，如式（9）和式（10）所示。$$ {\overset{\smile} X} = {\boldsymbol{\hat X}} - {{\boldsymbol{Q}}_{{\boldsymbol{\hat X\hat N}}}}{\boldsymbol{Q}}_{{\boldsymbol{\hat N}}}^{ - 1}({\boldsymbol{\hat N}} - {\overset{\smile} {\boldsymbol{X}}}) $$ (9) $$ {{{{\boldsymbol{Q}}}}_{\overset{\smile} X}} = {{{{\boldsymbol{Q}}}}_{{{\hat X}}}} - {{{{\boldsymbol{Q}}}}_{{{\hat X\hat N}}}}{{{\boldsymbol{Q}}}}_{{{\hat N}}}^{ - 1}{{{{\boldsymbol{Q}}}}_{{{\hat N\hat X}}}} $$ (10) 2.2 高精度北斗相对定位解算软件
高精度北斗差分定位解算软件使用独特的周跳探测与修复和部分模糊度快速固定技术来提高系统的精度、连续性、完好性，并且在干扰和部分遮挡环境下，仍然能提供高精度的定位信息。
准确探测周跳是北斗高精度载波相位测量的关键问题。周跳会引起位置解算结果发生分米级以上的跳变，影响灾变评估和预警分析。目前广泛使用的TurobEdit探测法[9]由于其中的MW（Melbourne-Wubeena ）组合包含伪距观测，受多路径效应和卫星高度角的影响，可能无法探测到1～2周的小周跳。使用小波、经验模分解等信号降噪的方法降低MW组合观测值的噪声，有效降低探测量噪声后，能够探测出所有的小周跳。
使用基于位置约束的多频模糊度融合解算方法，将多频宽巷直接固定法与LAMBDA搜索固定方法联合，逐级固定模糊度。使用部分模糊度固定的概念，通过浮点解验后方差估计，对双差残余误差较大的观测值进行判别和筛选，利用测量条件和几何结构最优的模糊度子集进行固定，提升固定成功率，增加北斗高精度解算的可用性和实时性。
2.3 北斗三代与GPS定位精度对比
北斗三代与GPS定位精度对比的试验数据来自某北斗监测站，该监测站的接收机能同时接收北斗数据和GPS数据，如图3、图4及表3所示。
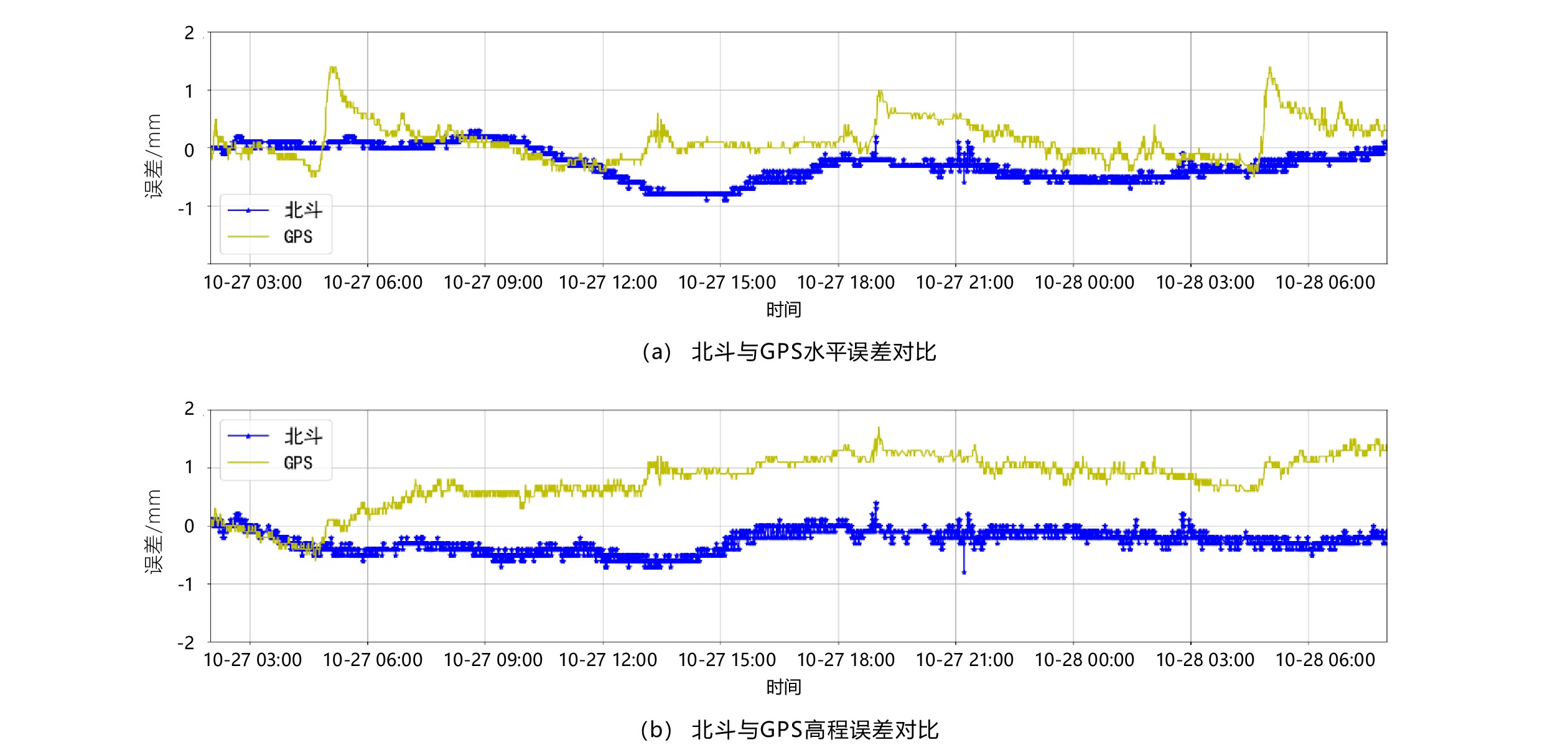
表 3 北斗与GPS定位误差对比卫星定位系统 定位中误差/mm 平均卫星个数/个 水平 高程 北斗三代 0.29 0.18 13.97 GPS 0.35 0.46 7.43 从以上图、表可知，北斗卫星个数明显多于GPS；北斗卫星几何结构优良，定位误差明显低于GPS；北斗三代系统在变形监测方面具有显著优势。
3 基线长度测试与分析
试验现场包括一个北斗三代监测站和一套北斗区域增强系统，增强系统中距离北斗监测站最近的两个基准站距离分别为1 km和3 km，北斗监测站的接收机天线安装在沉降和位移平台上进行测试。在试验过程中，我们使用测试台不断调整沉降和位移量，通过解算变形量与实际调整变形量的对比来分析不同基线长度下北斗三代系统解算精度。
3.1 1 km基准站北斗数据分析
图5和图6分别为1 km基站的北斗实测数据与标定台数据的对比曲线。可以明显看出，当每一级标定台位移变化时，北斗实测数据均紧跟着发生变化，且变化趋势一致。1 km基站的位移数据较沉降数据更加稳定，与标定台数据非常吻合。
表4和表5分别为1 km基站的水平位移和竖直沉降数据统计情况。在整个标定过程中，水平位移共调整了4次，内符合精度在0.227～0.351mm，外符合精度在0.427～1.574 mm。竖直沉降共调整了4次，内符合精度在0.146～1.456 mm，外符合精度在0.979～2.150 mm。
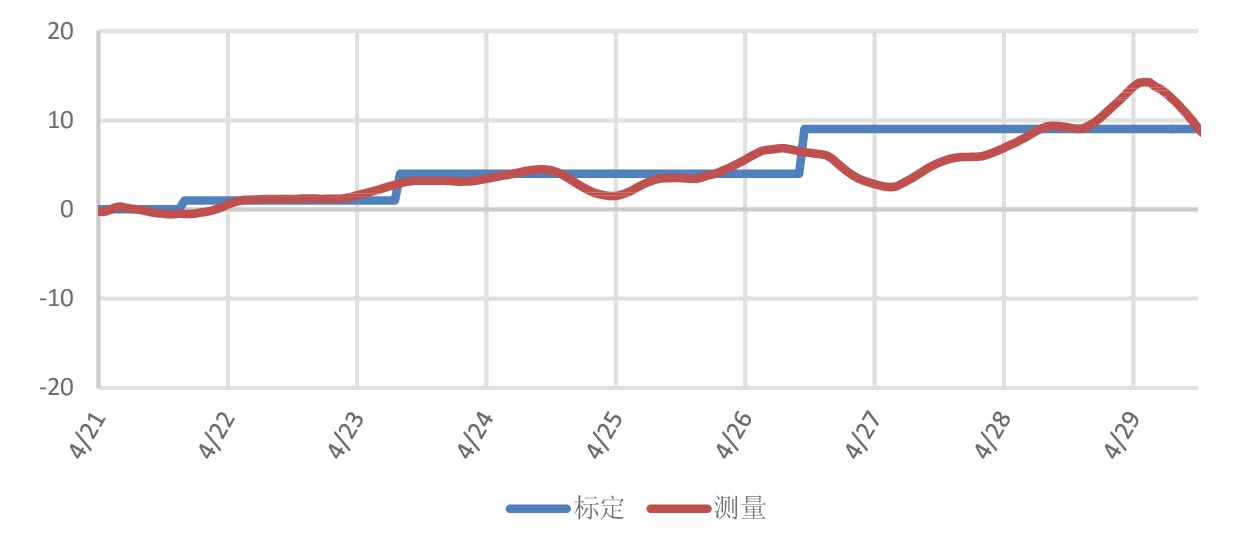
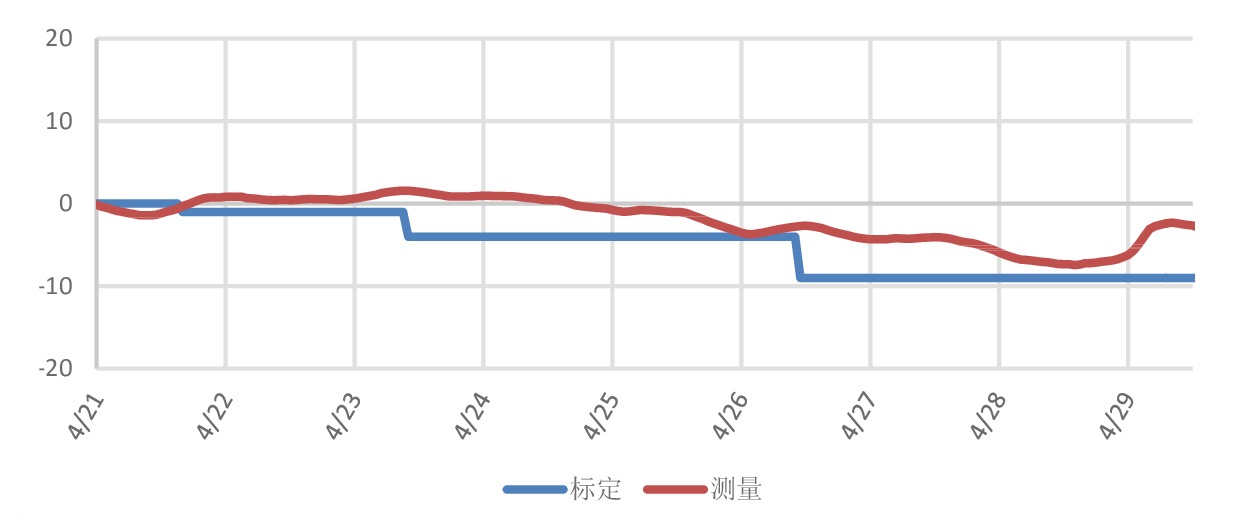
表 4 1 km基站水平位移统计测次 标定平台水平位移/mm 实测水平位移/mm 内符合精度/mm 外符合精度/mm 本次变化量 累计位移量 本次变化量平均值 累计位移量平均值 第1次 1 1 0.674 0.872 0.277 0.427 第2次 3 4 3.67 4.541 0.329 0.746 第3次 5 9 3.466 8.007 0.351 1.574 第4次 17 26 15.942 23.949 0.287 1.096 表 5 1 km基站竖直沉降统计测次 标定平台沉降/mm 实测沉降/mm 内符合精度/mm 外符合精度/mm 本次变化量 累计位移量 本次变化量平均值 累计位移量平均值 第1次 −1 −1 −2.001 −2.901 0.146 1.011 第2次 −3 −4 −1.086 −3.986 0.383 1.952 第3次 −5 −9 −4.126 −8.112 0.440 0.979 第4次 −17 −26 −18.582 −26.694 1.456 2.150 3.2 3 km基准站北斗数据分析
图7和图8分别为3 km基站的北斗实测数据与标定台数据的对比曲线。可以发现，当每一级标定台位移变化时，北斗实测数据均紧跟着发生变化，且变化趋势一致。相对于1 km基站的数据来看，3 km基站的数据波动幅值更大。
表6和表7分别为3 km基站的水平位移和竖直沉降数据统计情况。在整个标定过程中，水平位移共调整了4次，内符合精度在0.540～2.772 mm，外符合精度在1.000～2.723 mm。竖直沉降共调整了4次，内符合精度在0.340～2.083 mm，外符合精度在1.161～4.884 mm之间。受到双差残余误差影响，3 km基线下监测精度相对1 km基线存在显著下降，但仍控制在5 mm以内。
表 6 3 km基站水平位移统计测次 标定平台水平位移/mm 实测水平位移/mm 内符合精度/mm 外符合精度/mm 本次变化量 累计位移量 本次变化量平均值 累计位移量平均值 第1次 1 1 1.842 1.692 0.540 1.000 第2次 3 4 2.449 4.140 1.711 1.798 第3次 5 9 5.088 9.228 2.772 2.723 第4次 17 26 16.287 25.515 1.748 1.888 表 7 3 km基站竖直沉降统计测次 标定平台沉降/mm 实测沉降/mm 内符合精度/mm 外符合精度/mm 本次变化量 累计位移量 本次变化量平均值 累计位移量平均值 第1次 −1 −1 1.699 0.776 0.340 2.720 第2次 −3 −4 −2.721 −1.945 1.127 1.161 第3次 −5 −9 −3.382 −5.327 1.716 2.359 第4次 −17 −26 −21.418 −26.745 2.083 4.884 3.3 实验结果
通过试验结果可以看出，北斗三代的定位服务性能已超过GPS，在变形监测中可获得优于GPS的结果。铁路监测预警系统采用区域增强、北斗高精度定位、多回路通信、监测预警等多种技术，可协助快速掌握铁路沿线灾害状况，实现对隐患点地质灾害的预测。
4 结束语
本文设计了铁路北斗三代高精度监测预警系统，解决了铁路变形监测实时高精度监测和预警问题，为北斗三代系统在铁路领域的应用提供了重要的思路。未来，本文将继续研究北斗三代系统在铁路中的系统应用，探索铁路北斗增强系统和多源融合监测的新思路，以实现对铁路隐患进行全覆盖、高精度、自动化监测的目标。
-
表 1 各子系统的功能及其构成
子系统名称 功能 构成 基准站网 负责卫星定位数据和大气数据的采集、接收、传输；
负责设备完好性的监测北斗接收机；
电源；
网络设备；
避雷设备；
气象监测设备控制与数据中心 负责参考站信息管理；
系统管理与维护；
数据分流与处理；
信息编码与解码数据处理服务器组；
网络设备；
数据收发设备；
电源保障设备高速数据通信网 负责各子系统数据的传输 有线通信；
蜂窝网络；
天基通信运营服务 负责用户管理与鉴权；
监测用户定位状态；
将生成的差分数据产品播发至监测站运营服务器组；
运营软件
下载: 导出CSV
表 4 1 km基站水平位移统计
测次 标定平台水平位移/mm 实测水平位移/mm 内符合精度/mm 外符合精度/mm 本次变化量 累计位移量 本次变化量平均值 累计位移量平均值 第1次 1 1 0.674 0.872 0.277 0.427 第2次 3 4 3.67 4.541 0.329 0.746 第3次 5 9 3.466 8.007 0.351 1.574 第4次 17 26 15.942 23.949 0.287 1.096
下载: 导出CSV
表 5 1 km基站竖直沉降统计
测次 标定平台沉降/mm 实测沉降/mm 内符合精度/mm 外符合精度/mm 本次变化量 累计位移量 本次变化量平均值 累计位移量平均值 第1次 −1 −1 −2.001 −2.901 0.146 1.011 第2次 −3 −4 −1.086 −3.986 0.383 1.952 第3次 −5 −9 −4.126 −8.112 0.440 0.979 第4次 −17 −26 −18.582 −26.694 1.456 2.150
下载: 导出CSV
表 6 3 km基站水平位移统计
测次 标定平台水平位移/mm 实测水平位移/mm 内符合精度/mm 外符合精度/mm 本次变化量 累计位移量 本次变化量平均值 累计位移量平均值 第1次 1 1 1.842 1.692 0.540 1.000 第2次 3 4 2.449 4.140 1.711 1.798 第3次 5 9 5.088 9.228 2.772 2.723 第4次 17 26 16.287 25.515 1.748 1.888
下载: 导出CSV
表 7 3 km基站竖直沉降统计
测次 标定平台沉降/mm 实测沉降/mm 内符合精度/mm 外符合精度/mm 本次变化量 累计位移量 本次变化量平均值 累计位移量平均值 第1次 −1 −1 1.699 0.776 0.340 2.720 第2次 −3 −4 −2.721 −1.945 1.127 1.161 第3次 −5 −9 −3.382 −5.327 1.716 2.359 第4次 −17 −26 −21.418 −26.745 2.083 4.884
下载: 导出CSV
-
[1] 龚大亮, 陈细秋. 基于北斗的灾害监测预警系统设计[C]//中国全球卫星定位系统技术应用协会. 中国全球卫星定位系统技术应用协会年会论文集. 北京: 测绘出版社, 2010: 235-238. [2] 张同伟,李凌瑛. 基于北斗系统的地质灾害监测系统建设 [J]. 电气技术,2021,22(1):99-103. DOI: 10.3969/j.issn.1673-3800.2021.01.020 [3] 杨加斌,崔高峰,赵 海,等. 基于北斗的铁路构筑物安全监测系统及应用 [J]. 卫星应用,2019(7):35-39. DOI: 10.3969/j.issn.1674-9030.2019.07.013 [4] 段亚龙. 基于北斗系统的输电线路地质灾害监测预警系统建设及应用 [J]. 工程建设与设计,2021(2):153-154. DOI: 10.13616/j.cnki.gcjsysj.2021.01.268 [5] 陈 榕. 京沈客专边坡形变监测平台数据分析展示子系统的设计与实现[D]. 南京: 南京大学, 2018. [6] 秦 健,潘佩芬,陶 承. 铁路北斗地基增强系统构建及基准站选址研究 [J]. 铁路计算机应用,2018,27(3):11-14. DOI: 10.3969/j.issn.1005-8451.2018.03.003 [7] 甘 雨. GNSS/INS组合系统模型精化及载波相位定位测姿[D]. 郑州: 中国人民解放军战略支援部队信息工程大学, 2015. [8] TEUNISSEN P J G. The least-square ambiguity decorrelation adjustment: a method for fast GPS integer ambiguity estimation [J]. Journal of Geodesy, 1995(70): 65-82.
[9] BLEWITT G. An automatic editing algorithm for GPS data [J]. Geophysical Research Letters, 1990, 17(3): 199-202. DOI: 10.1029/GL017i003p00199
-
期刊类型引用(1)
1. 吴强，屈利杰. 基于ARIMA和XGBoost算法的辅逆系统故障预测. 大连交通大学学报. 2021(01): 96-100 . 
百度学术
其他类型引用(3)
计量
- 文章访问数: 150
- HTML全文浏览量: 152
- PDF下载量: 53
- 被引次数: 4
