Prediction method of train operation delay of Beijing-Shanghai High-speed Railway
-
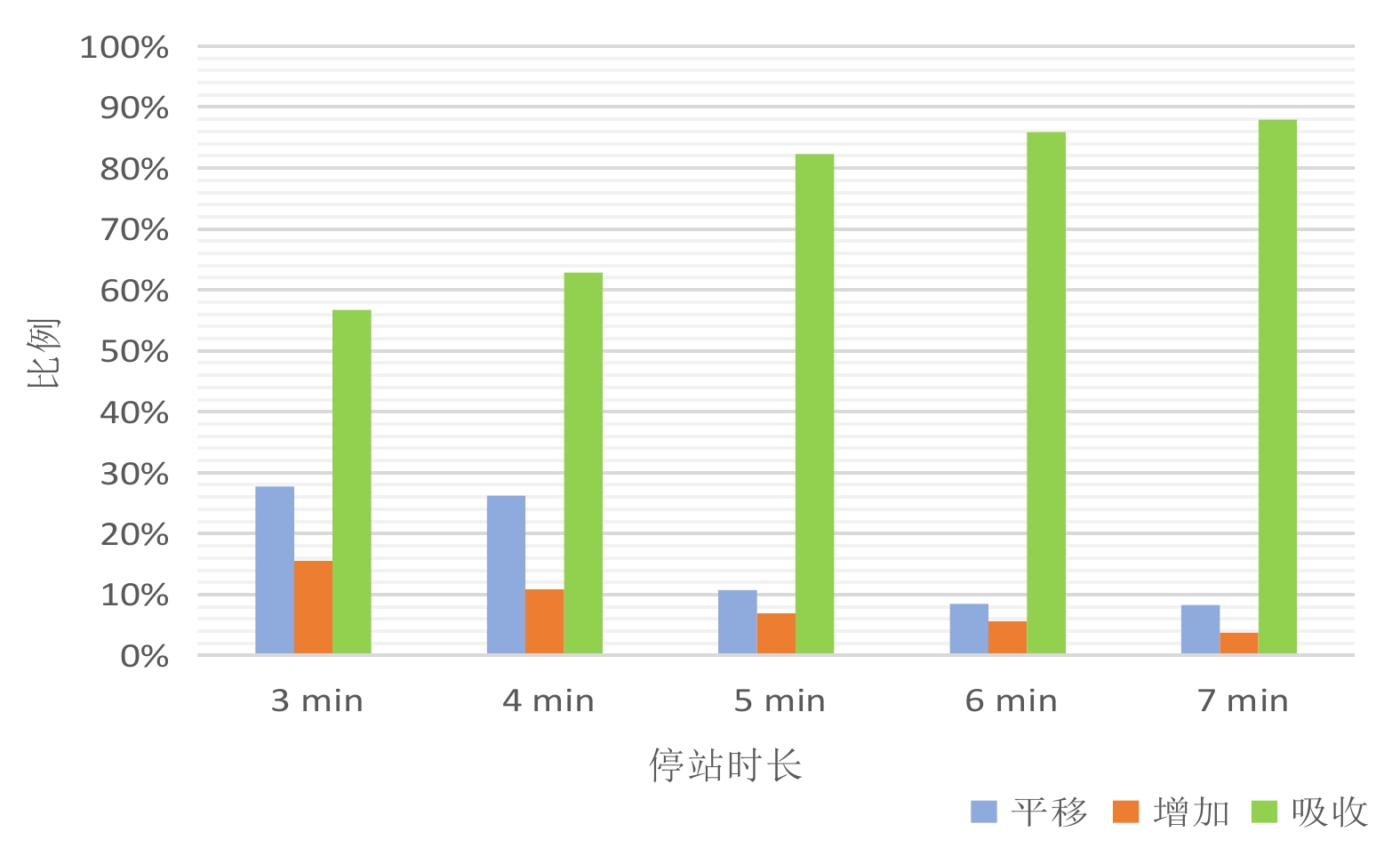
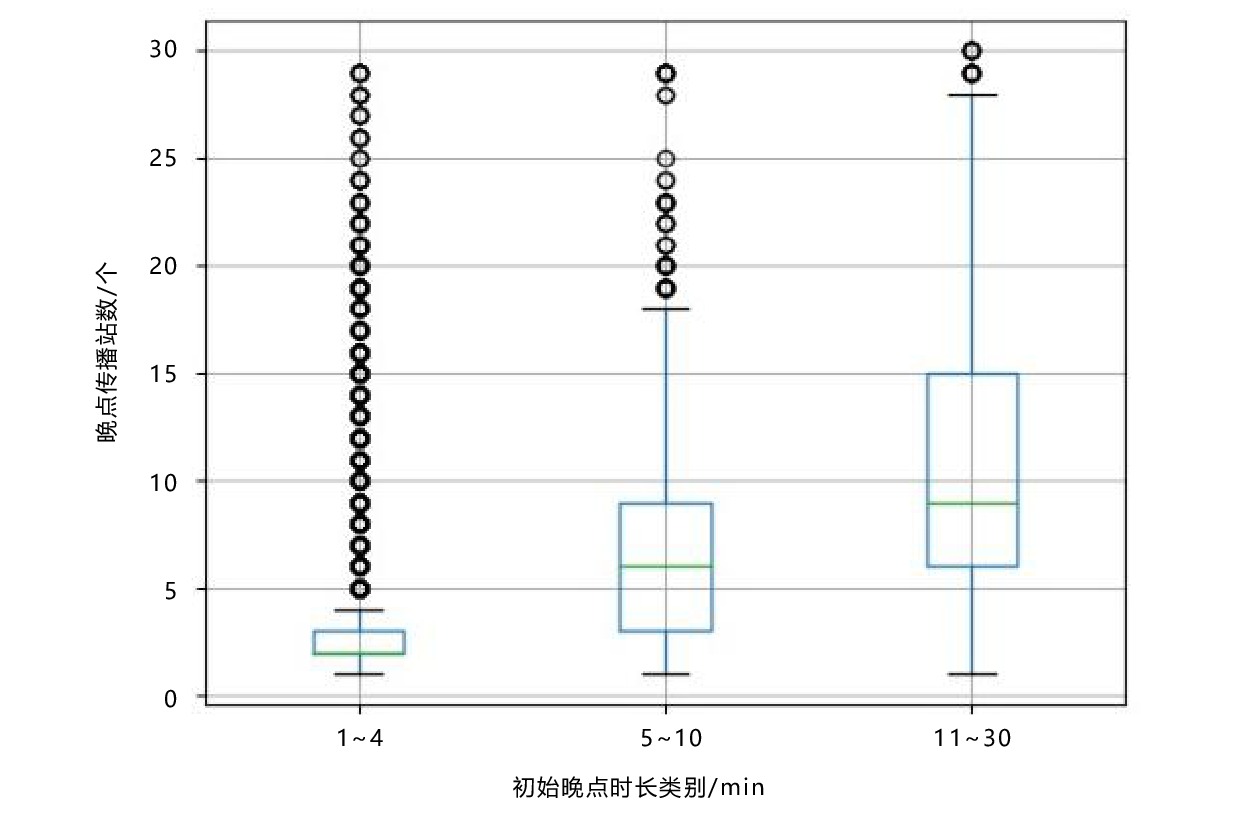
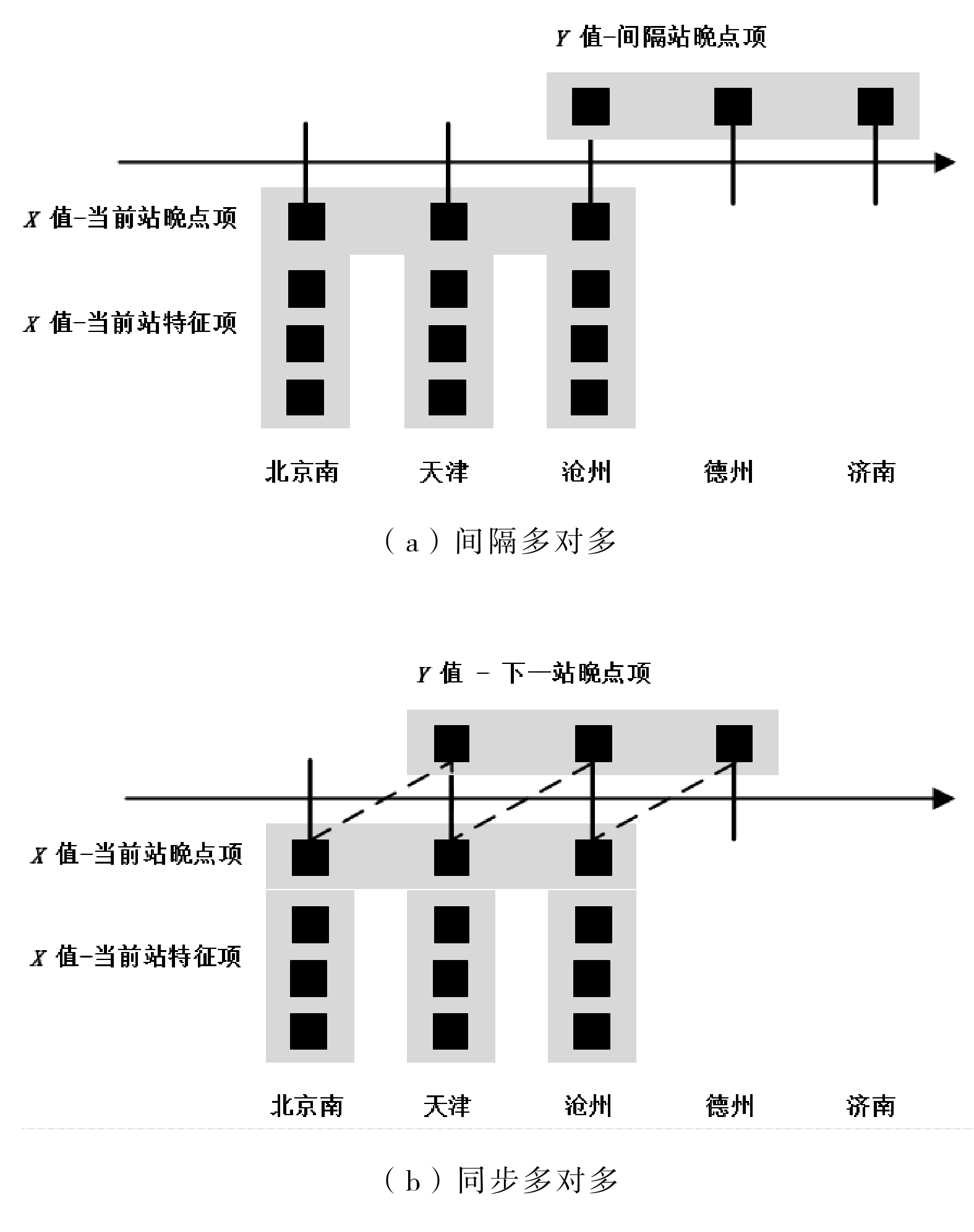
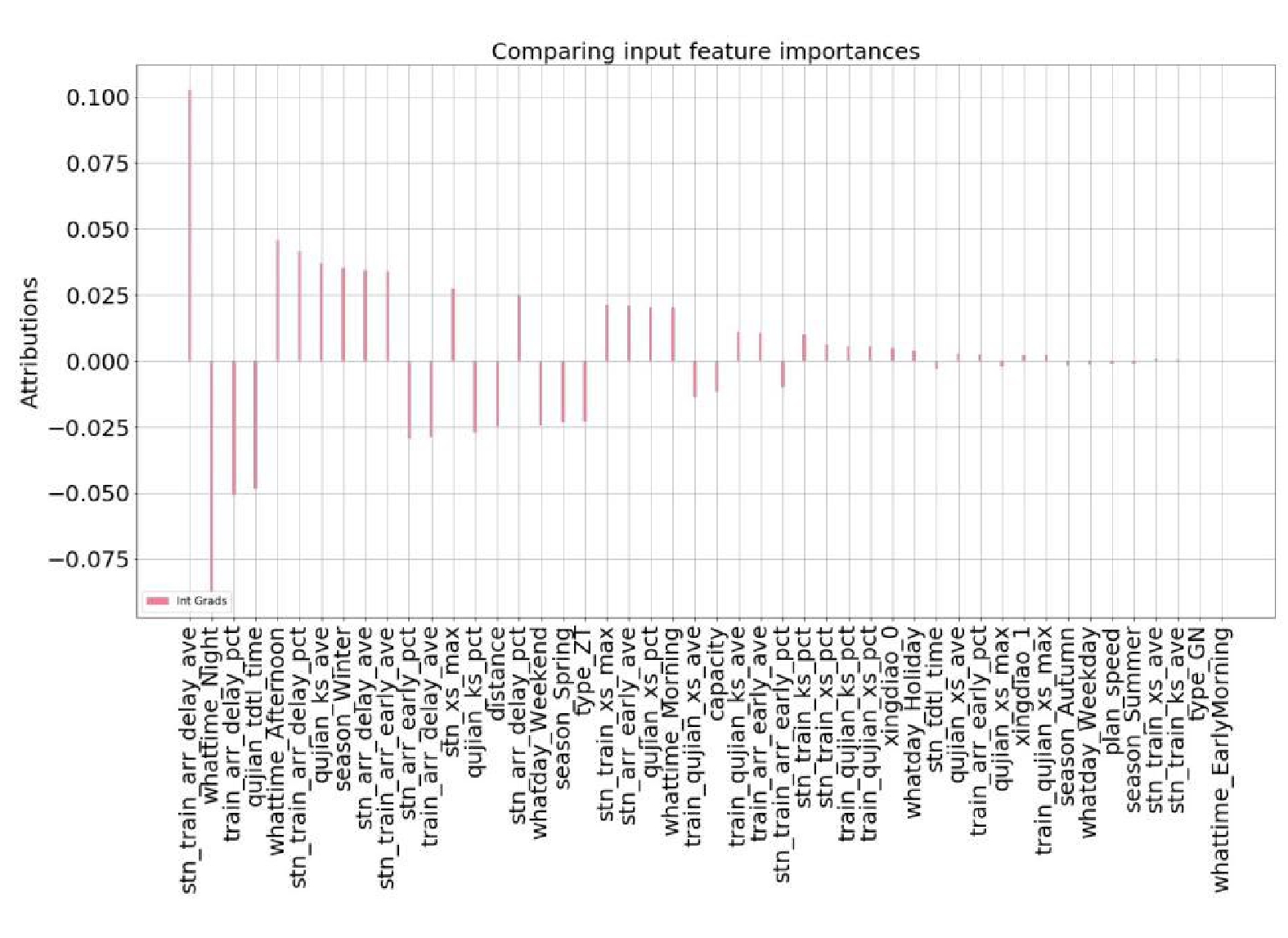
摘要: 为快速、准确地掌握列车的运行状态及未来的运行趋势,需要对列车运行晚点预测方法进行深入研究。文章根据对北京—上海高速铁路(简称:京沪高铁)2020年列车运行数据的分析,包括停站时长对于晚点的影响及不同初始晚点时长下的传播车站数,提出了基于循环神经网络(RNN,Recurrent Neural Network)的全段预测方法,使用同步多对多模式的RNN模型作为基础模型结构,建立列车运行晚点预测模型。在特征值的选择上,采用集成梯度打分法,从多个特征值中选择12个最显著的变量作为模型自变量。采用该模型对京沪高铁2020年晚点数据进行验证,结果表明,该模型在验证集上5 min的误差范围内可以达到89%的准确率,该预测方法可以满足实际生产的需要,有助于调度部门进行科学决策,有利于提升铁路旅客服务质量。Abstract: In order to quickly and accurately grasp the train operation status and future operation trend, it is necessary to deeply study the prediction method of train operation delay. Based on the analysis of the train operation data of Beijing-Shanghai High-speed Railway in 2020, including the impact of dwell time on delay and the number of propagation stations under different initial delay time, this paper put forward a full section prediction method based on Recurrent Neural Network(RNN), and used the RNN model of synchronous many to many mode as the basic model structure, established a prediction model of train operation delay. In the selection of eigenvalues, the paper used the integrated gradient scoring method to select the 12 most significant variables from multiple eigenvalues as the independent variables of the prediction model, and verified the delay data of Beijing-Shanghai High-speed Railway in 2020 by the prediction model. The verification results show that the model can achieve 89% accuracy within the error range of 5 minutes on the verification set. The prediction method can meet the needs of actual production, help the dispatching department make scientific decisions and improve the quality of railway passenger service.
-
近年来,铁路货运运量持续增长,货运收入在铁路运输总收入中的比重不断增大。为获取较大的市场占有率和较好的利润增长速度,中国国家铁路集团有限公司(简称:国铁集团)及各铁路局集团公司根据运输需求、竞争行业货物运价变化等市场行情动态,制定了一系列铁路货运一口价议价策略(简称:一口价策略)[1]。作为铁路企业内部经济监督和独立评价机制的重要组成部分,铁路审计人员需要审查货物运价实际执行情况与规定的一口价策略是否一致。
一口价策略以非结构化文本形式存储,审计人员在审查货物运价实际执行情况与规定的一口价策略是否一致时,需要通过繁琐的人工操作,将一口价策略信息从文本数据中抽取出来,无法将一口价策略文本数据高效地转化为信息,制约了审计作业效率的提升。
命名实体识别技术可从自然语言文本中识别出相关或特定意义的实体信息,并进行结构化处理。目前,基于传统机器学习方法的条件随机场(CRF ,Conditional Random Field)模型[2]、深度学习与CRF相结合的双向长短时记忆 (BiLSTM ,Bidrectional Long Short Term Memory)-CRF模型[3]、卷积神经网络(CNN ,Convolutional Neural Network)-BiLSTM-CRF模型[4],以及通过Attention机制直接对文本序列建模的Transformer模型等在命名实体识别领域均有较好的性能表现[5]。
在航空领域,汪政等人[6]设计了基于中文分词和实体解析的航变信息提取模型,提高了航班实体信息识别准确率;在电力领域,杨炜等人[7]建立了基于半监督学习的电网设备故障报告实体信息提取模型,有效减少了电网领域命名实体识别对人工标注的依赖;在桥梁病害检测领域,李韧等人[8]基于Transformer-BiLSTM-CRF模型,识别出桥梁检测文本中的桥梁结构构件和检测病害等关键业务信息,促进了桥梁管理养护的智能化发展。在铁路文本数据命名实体识别方面,目前已有许多学者开展了应用研究。赵瑞晨[9]构建了基于字嵌入+BiLSTM+CRF的铁路事故文本命名实体识别模型,可有效识别铁路事故命名实体;李新琴等人[10]以高速铁路信号设备故障文本数据为基础,建立了故障知识自动抽取模型,为高速铁路设备故障诊断提供了知识库;杨连报等人[11]通过构建BERT(Bidirectional Encoder Representation from Transformers)-BiLSTM-CRF模型,实现了对铁路故障文本向量的计算和识别,以此得到铁路文本命名实体识别结果信息。
在一口价策略实体信息识别方面,目前开展的研究工作较少。本文基于上述研究,针对一口价策略文件的数据特点,提出RoBERTa(A Robustly Optimized BERT)-BiLSTM-CRF模型,实现对一口价策略命名实体信息的自动识别。
1 一口价策略文本数据说明及标注策略
1.1 数据说明
一口价议价策略以文本数据的形式保存,主要包括项目号、托运人、运费价差系数、考核运量、考核时间等相关信息[12]。同一铁路局集团公司的一口价策略文件的行文方式相似,但不同铁路局集团公司间的文件存在较大差异,增加了文本内容的复杂性和多样性。从一口价策略的文本数据中提取出审计信息,并生成结构化二维数据表,是对货物运价实际执行情况进行高效审查的重要步骤。
1.2 命名实体信息定义及标注
为审查货物运价实际执行情况与规定的一口价策略是否一致,本文定义了一口价策略命名实体信息,如表1所示[12]。
表 1 一口价策略命名实体信息列表序号 实体名称 标注标识 序号 实体名称 标注标识 1 项目号 N(Number) 7 新增发站站名 NS(New-Start) 2 托运人 P(People) 8 取消发站站名 CS(Cancel-Start) 3 价差系数 C(Coefficient) 9 到站站名 A(Arrive) 4 考核有效期 T(Time) 10 新增到站站名 NA(New-Arrive) 5 考核运量 F(Freight) 11 取消到站站名 CA(Cancel-Arrive) 6 发站站名 S(Start) 对命名实体信息进行定义后,需进行数据标注。本文采用某铁路局集团公司2019—2021年的一口价策略文件作为数据集,使用BIO(Beginning,Inside,Outside)标注方案对其进行标注。其中,B(Beginning)标注实体的开始部分;I(Inside)标注实体的中间部分;O(Outside)标注与实体无关的信息。
2 模型设计
本文设计的RoBERTa-BiLSTM-CRF模型分为RoBERTa层、BiLSTM层和CRF层,模型架构如图1所示。其中,RoBERTa层利用RoBERTa模型 [13],将一口价策略文本数据转换为特征向量;BiLSTM层使用BiLSTM神经网络,学习文本中的上下文特征信息,输出命名实体类别分数值;CRF层对BiLSTM层的输出结果进行修正,并输出命名实体类别。
2.1 RoBERTa层
在将一口价策略文件的文本数据输入BiLSTM层前,需要对训练样本进行向量化表示。BERT模型是一个基于Transformer处理单元的预训练模型 [14],具有丰富的先验语义知识,能够使不同语句序列中相同的单词获得不同的语义表示,解决传统文本表示模型存在的不能动态进行特征表示及特征表示能力不足等问题。本文采用的RoBERTa模型在BERT模型基础上进行了改进,主要包括:在规模更大的公开数据集上进行预训练;对BERT模型的训练策略进行了优化,使其具有更多的模型参数。RoBERTa层架构如图2所示,
Wi 代表输入的汉字。2.2 BiLSTM层
BiLSTM神经网络既能提取当前时刻之前的信息,又能利用当前时刻之后的信息,因此,本文利用该神经网络来学习一口价策略文件中的上下文信息。BiLSTM神经网络由前向LSTM层和后向LSTM层组成,输出结果为每个字符属于每个实体类别的分数值,BiLSTM层架构如图3所示。
2.3 CRF层
CRF层的作用是对BiLSTM层的输出结果进行修正。若一句话有
n 个字,每个字有m 种可能的标签,则这句话可能的标签序列共有mn 个。CRF层通过学习标签序列之间的相邻依赖关系,给每一个可能的标签序列打分,得分最高的即为最优标签序列,并以此确定命名实体类别。设一个输入序列为
X={x1,x2,⋯,xn} ,xi 为序列 X 中的第 i 个输入文字,i=1,2,⋯,n ,其对应的模型预测标签序列为ˆy={ˆy1,ˆy2,⋯,ˆyn} ,ˆyi 表示模型预测出xi 对应的标签概率向量,则该预测序列标签的得分为[11]Score(X,ˆy)=n∑i=1Wˆyi,ˆyi+1+n∑i=1Pi,ˆyi (1) 其中,
W 表示状态转移矩阵,是CRF层的学习参数,Wˆyi,ˆyi+1 表示ˆyi 转移到ˆyi+1 的概率得分;将BiLSTM层的输出作为矩阵P,Pi,ˆyi 是第 i 个字符被标记为ˆyi 的概率得分。通过求Score(X,ˆy) 的最大值可得到最优标签序列。3 应用验证
3.1 数据增强
为提高模型的训练效果,本文采用以下2种方法进行训练样本数据增强。
3.1.1 基于同类型实体替换的数据增强
同类型实体替换是指将样本中某个实体随机替换为另一个同类型的实体,具体步骤为:(1)通过人工标注提取出一口价策略文本中的命名实体信息,并分类保存;(2)对一句话中的同类型命名实体信息进行替换,将替换后的样本作为扩展样本保存。例如
样本1:项目号[000001]项目号:新增到站[A]新增到站站名站。
样本2:项目号[000002]项目号:新增发站[B]新增发站站名站,新增到站[C]新增到站站名站。
用样本2的新增到站站名替换样本1中的新增到站站名,得到扩展样本1:项目号[000001]项目号:新增到站[C]新增到站站名站。
3.1.2 基于随机噪声的数据增强
基于同类型实体替换的数据增强会增加训练样本中语句的相似性,使得模型训练易出现过拟合。为防止上述情况,并增强模型的泛化能力,本文在非命名实体信息的位置上添加随机噪声。常用的随机噪声方法包括随机删除单词、随机插入单词、同音字替换、颠倒用字顺序等。一口价策略文件的文本数据中包含命名实体信息的语句密度较大,不适合随机删除单词。本文采用在非命名实体信息的位置随机插入停用词(本文停用词采用哈工大的停用词表)的方法来增加训练样本的噪声。例如
样本3:项目号[000003]项目号:[A]发站发往[B]到站的[货物C]货物品名,实施竞争性一口价,考核运量[D吨/月]考核运量。
在样本3的非实体位置插入停用词,得到扩展样本3:项目号[000003]项目号:{对于}插入停用词[A]发站发往[B]到站的[货物C]货物品名,实施竞争性一口价,考核运量[D吨/月]考核运量。
3.2 模型训练
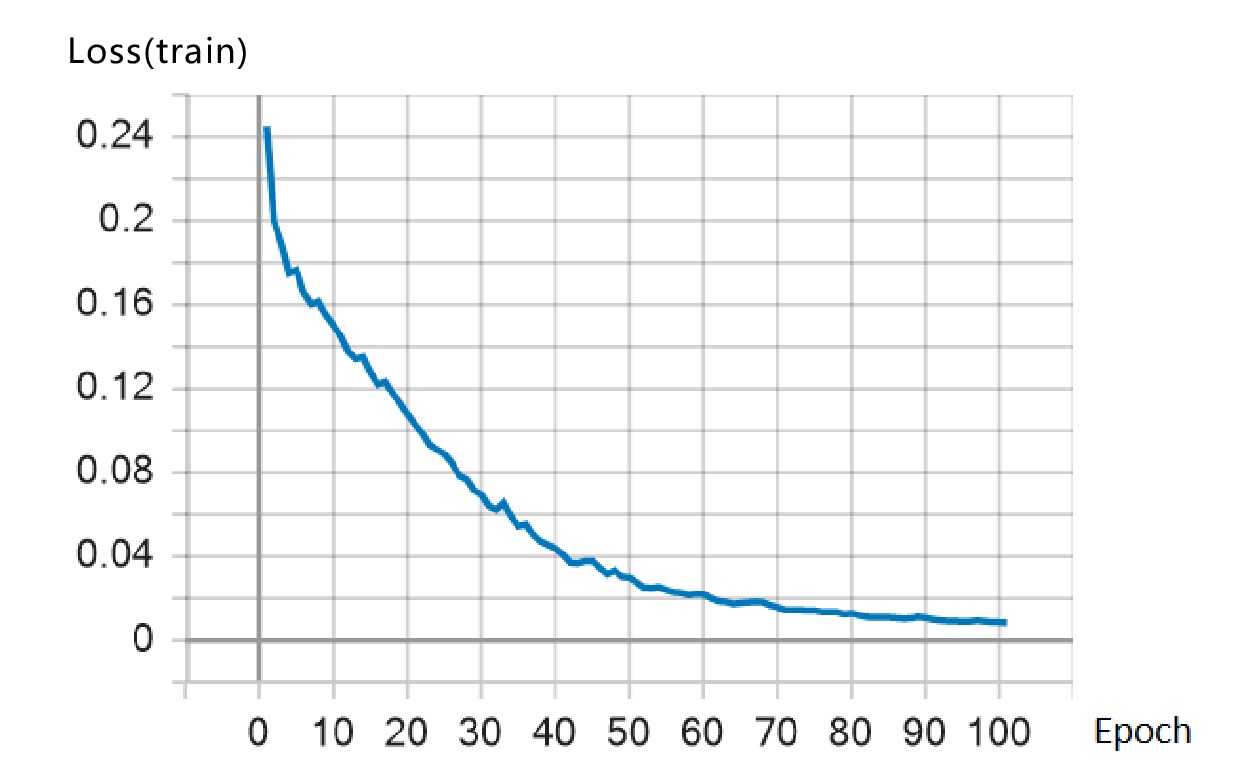
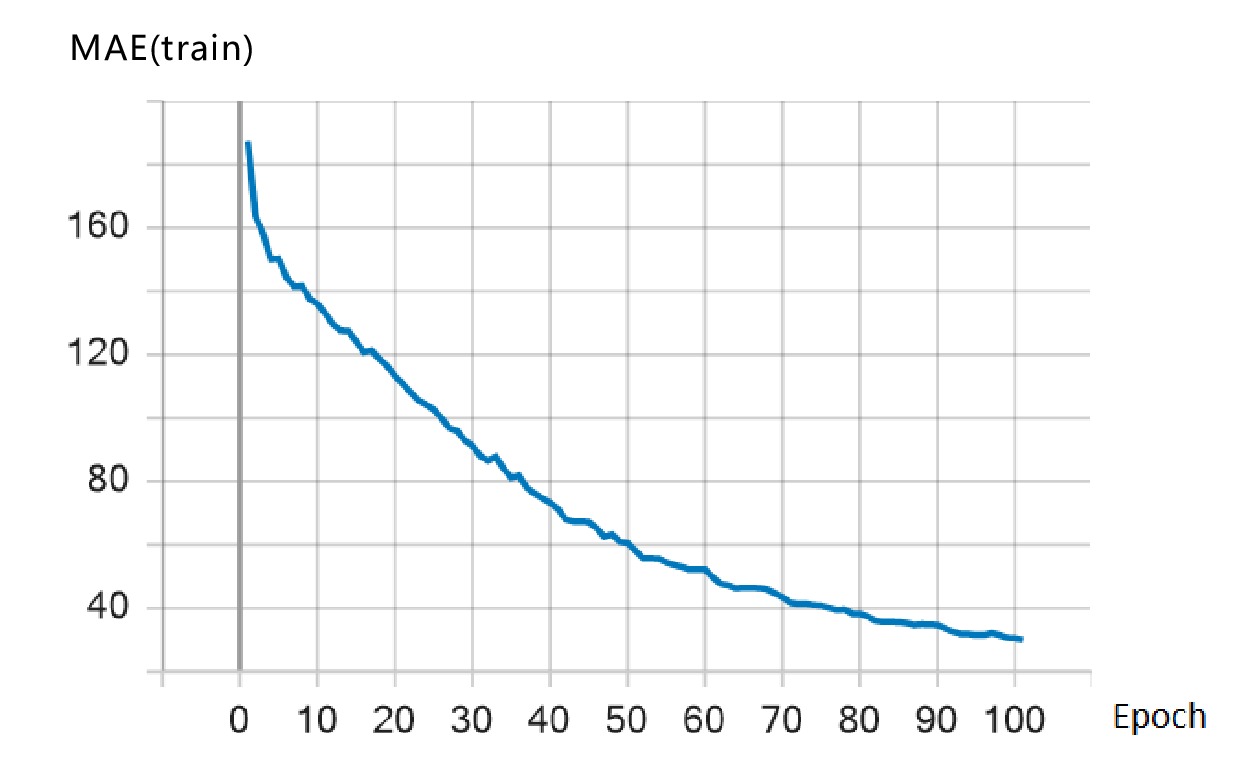
本文采用Tensorflow 2.3框架,将增强后的数据输入到RoBERTa-BiLSTM-CRF模型中。将模型的 Batch_size设为5,句子序列长度设置为1024。使用RoBERTa模型进行字向量转换,隐藏层维度设为128,学习率设为0.00001;BiLSTM神经网略的隐藏层神经元个数设为100,Dropout设为0.5,优化器采用Adam优化算法,学习率设为0.0002。训练过程中,损失函数的变化如图4所示。
由图4可知,随着训练轮数的增加,损失函数的值不断下降并趋于平稳,说明基于以上参数设置的RoBERTa-BiLSTM-CRF模型训练达到了收敛状态。
3.3 评价指标
本文采用准确率P、召回率R和F值F作为模型性能的评价指标,3者的值越大代表模型的性能越好,计算公式分别为
P=正确识别的命名实体数识别出的命名实体数⋅100% (2) R=识别的命名实体数文本包含的命名实体数⋅100% (3) F=2⋅P⋅RP+R⋅100% (4) 3.4 模型试验及对比分析
3.4.1 模型性能对比分析
本文选取某铁路局集团公司2019年一口价策略文本数据作为测试集,分别使用BiLSTM-CRF模型、BERT-BiLSTM-CRF模型和本文的RoBERTa-BiLSTM-CRF模型进行货物运价命名实体识别,计算得出的评价指标结果如表2所示。
表 2 模型评价指标对比模型名称 P R F BiLSTM-CRF 89.38% 90.10% 89.74% BERT-BiLSTM-CRF 91.15% 90.29% 90.72% RoBERTa-BiLSTM-CRF 94.69% 92.52% 93.59% 由表2可知,本文RoBERTa-BiLSTM-CRF模型的P、R和F相较于BiLSTM-CRF模型和BERT-BiLSTM-CRF模型均有一定程度的提升。对比结果表明,本文模型对于一口价策略中的命名实体有更好的识别效果。
3.4.2 样本数据对比分析
为验证数据增强后的训练样本对模型识别准确度的影响,本文分别使用未进行数据增强的训练样本和数据增强后的训练样本对RoBERTa-BiLSTM-CRF模型进行训练,并使用3.4.1中的测试数据对模型性能进行测试,测试结果如表3所示。
表 3 基于不同训练样本的模型的评价指标对比训练样本 P R F 未增强 87.61% 88.89% 88.25% 已增强 94.69% 92.52% 93.59% 由表3可知,采用数据增强后的样本进行训练的RoBERTa-BiLSTM-CRF模型在测试集上的P、R及F分别提高了7.08%、3.63%、5.34%,对一口价策略文件命名实体的识别效果有显著提升。
4 结束语
一口价策略命名实体识别是铁路货物运价审计中的重要内容。本文基于RoBERTa-BiLSTM-CRF模型,对一口价策略中的命名实体信息进行自动识别,同时,对训练数据集进行数据增强,扩大训练样本的规模,提高模型的命名实体识别准确性。与BiLSTM-CRF和BERT-BiLSTM-CRF模型相比,RoBERTa-BiLSTM-CRF模型的命名实体识别效果得到显著提升。
本模型对于多个策略合并或有梯度调整措施的一口价策略命名实体信息的识别效果不理想,后续可通过收集更多年份、更多铁路局集团公司的一口价策略文本数据来丰富训练样本的数量,提升模型训练效果。
-
表 1 12个最显著的特征值
序号 特征名 描述 1 stn_train_arr_early_ave 车次车站历史早到均值 2 whattime_EarlyMorning 00:00 — 06:00 whattime_Morning 06:00 — 12:00 whattime_Afternoon 12:00 — 18:00 whattime_Night 18:00 — 20:00 3 train_arr_delay_pct 车次历史晚到发生比例 4 qujian_tdtl_time 区间图定运行时间 5 stn_train_arr_delay_pct 车次车站历史晚到发生比例 6 qujian_ks_ave 区间历史晚到扩散均值 7 season_Spring 季节是否是春季 season_Summer 季节是否是夏季 season_Autumn 季节是否是秋季 season_Winter 季节是否是冬季 8 stn_arr_delay_ave 车站历史晚到时间均值 9 stn_train_arr_early_ave 车次车站历史早到均值 10 stn_arr_early_pct 车站历史早到发生比例 11 train_arr_early_ave 车次历史早到时间均值 12 stn_xs_max 车站历史晚到吸收最大值 表 2 模型训练参数
模型训练类型 参数设置 隐藏层层数 4 隐藏层神经元数 256 网络双向性 False 损失模型 Smooth L1 Loss 模型优化算法 Adam 初始学习率 1e-3,每10个Epoch衰减10% 训练Epoch次数 100 训练批次 16 验证批次 64 表 3 验证集的准确率
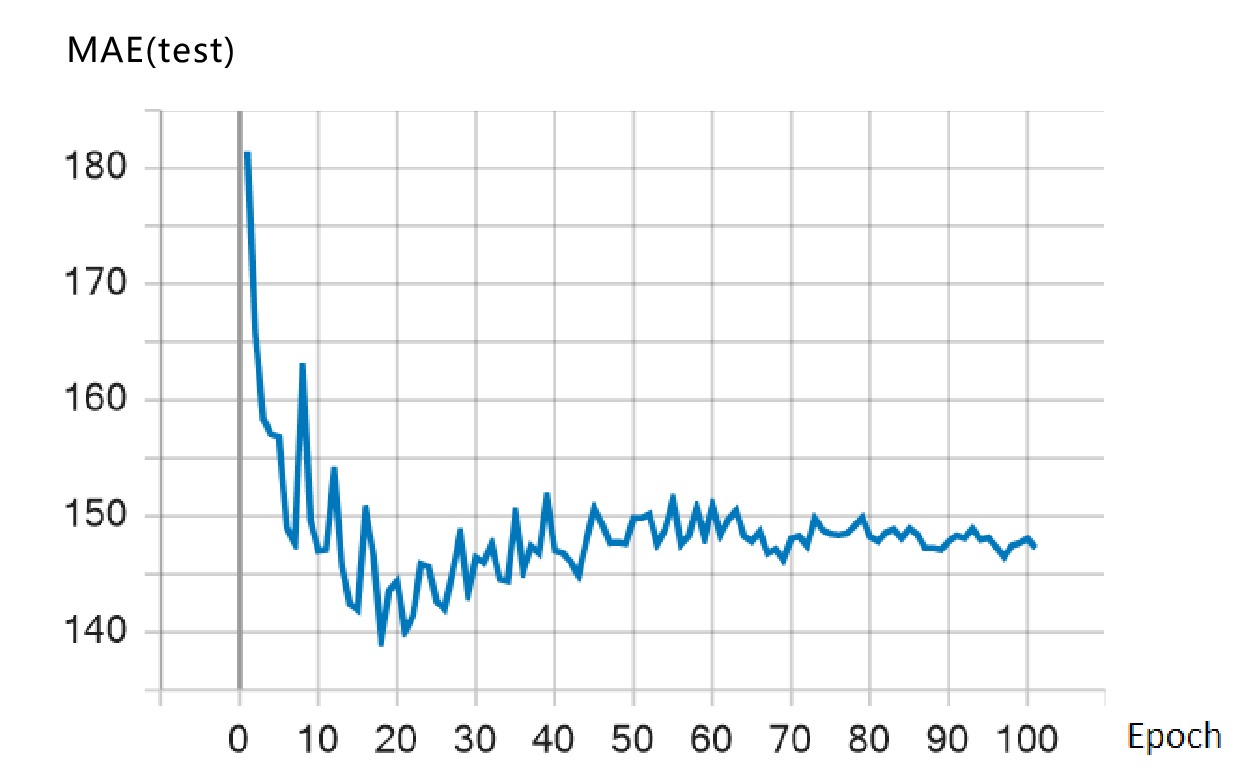
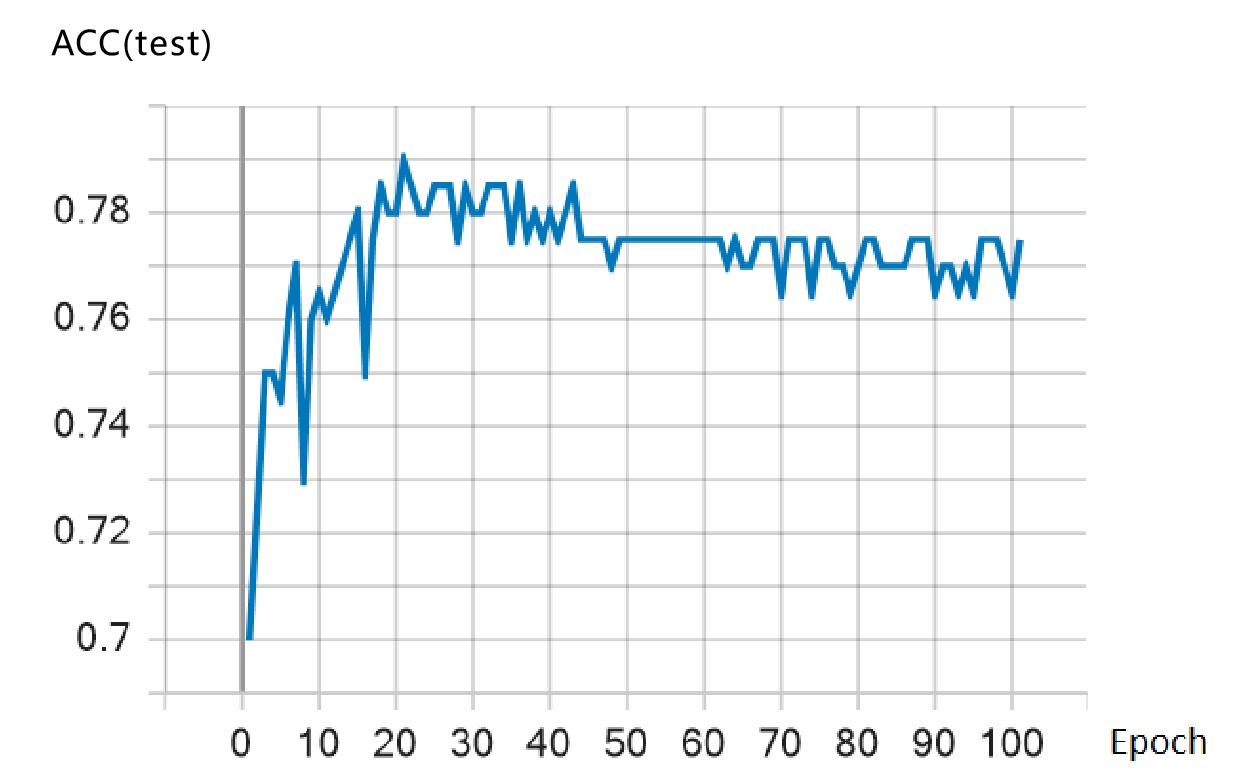
误差/min 验证集准确率 3 79% 5 89% 9 96% -
[1] Rob M. P. Goverde. A delay propagation algorithm for large-scale railway traffic networks [J]. Transportation Research Part C:Emerging Technologies, 2010, 18(3): 269-287. DOI: 10.1016/j.trc.2010.01.002
[2] BKER T, SEYBOLD B. Stochastic modelling of delay propagation in large networks [J]. Journal of Rail Transport Planning & Management, 2012, 2(1): 34-50.
[3] Pavle Kecman, Rob M. P. Goverde. Online data-driven adaptive prediction of train event times [J]. Transactions on Intelligent Transportation Systems, 2015, 16(1): 465-474. DOI: 10.1109/TITS.2014.2347136
[4] 黄 平,彭其渊,文 超,等. 高速铁路故障分类及其影响列车数模型 [J]. 中国安全科学学报,2018,28(增 2):46-53. [5] 庄 河,文 超,李忠灿,等. 基于高速列车运行实绩的致因-初始晚点时长分布模型 [J]. 铁道学报,2017,39(9):25-31. DOI: 10.3969/j.issn.1001-8360.2017.09.004 [6] 黄 平,文 超,李忠灿,等. 高速铁路列车晚点时间实时预测的神经网络模型 [J]. 中国安全科学学报,2019,29(增1):20-26. [7] 胡 瑞,文 超,张梦颖,等. 高速列车晚点预测的机器学习模型 [J]. 中国铁路,2019(11):72-77. [8] 张 琦,陈 峰,张 涛,等. 高速铁路列车连带晚点的智能预测及特征识别 [J]. 自动化学报,2020,45(12):2251-2259. [9] 胡雨欣,彭其渊,鲁工圆,等. 基于初始晚点和冗余时间 的列车晚点恢复时间预测模型 [J]. 交通运输工程与信息学报,2020,18(2):93-102. DOI: 10.3969/j.issn.1672-4747.2020.02.011 -
期刊类型引用(3)
1. 熊磊. 基于BERT的中药材治疗胃病的命名实体识别. 软件导刊. 2025(01): 57-64 .  百度学术
百度学术
2. 甘进龙,刘青,黄小飞. 基于RoBERTa-CNN-BiLSTM-CRF的“数据结构”课程知识命名实体识别. 信息系统工程. 2024(07): 60-63 .  百度学术
百度学术
3. 曾文驱,马自力,王淑营. 高速列车零部件知识图谱的智能问答知识子图匹配研究. 铁路计算机应用. 2023(12): 1-5 .  本站查看
本站查看
其他类型引用(1)




 下载:
下载: