Prediction model for displacement data of railway infrastructure
-
摘要: 线路安全是铁路运营的重要前提，我国铁路跨度广、行车环境复杂，当铁路基础设施稳定性产生改变时往往会严重影响行车安全。文章采用长短期记忆（LSTM ，Long Short-Term Memory）模型对基于全球导航卫星系统（GNSS，Global Navigation Satellite System）的铁路基础设施监测系统的形变监测数据进行建模预测，实现对铁路基础设施灾害的早期预警，并与多种传统时间序列预测模型进行对比，结果表明，LSTM模型具有更好的性能。Abstract: Railway safety is an important prerequisite for operation. Due to the wide span and complex driving environment of China's railway, when the stability of railway infrastructure changes, it will seriously affect the driving safety. This paper used Long Short-Term Memory(LSTM)model to model and predict the deformation monitoring data of railway infrastructure monitoring system based on Global Navigation Satellite System(GNSS), Achieved early warning of railway infrastructure disasters, and compared it with various traditional time series prediction models. The experimental results show that the LSTM model has better performance.
-
铁路作为我国基础设施建设的重要内容，在国民经济发展、国家安全战略、构建和谐社会等众多方面都扮演着不可或缺的角色。自2008年，我国高速铁路建设快速推进，更高的行车速度及更长的运营里程都对行车安全提出了更加严格的要求。由于铁路跨度广，其涉及的行车环境也更加复杂，当铁路基础设施稳定性产生改变时，往往会严重影响行车安全。例如边坡失稳造成的崩塌、滑坡，路基沉降引起的塌方等都是直接影响行车安全的潜在问题。因此，对铁路基础设施进行实时位移监测和精准预报预警是十分必要的。
针对时间序列预测算法的研究一直伴随着机器学习算法的相关研究而发展，并成功地将一系列经典的机器学习模型应用于电力[1]、交通[2]、气象[3]等受固定时间周期影响的领域。综合来看，对于短期内时间相关性强的数据，尽管通过简单的机器学习模型已能达到较好的效果，但仍然有许多问题需要进一步解决，比如人工依赖性强、建立过程复杂、模型只能针对具体单一场景、泛化能力差等。
随着深度学习技术的成熟，循环神经网络（RNN，Recurrent Neural Networks）[4]被广泛地应用于时间序列建模分析，但其本身存在较严重的梯度爆炸、梯度弥散及长期依赖的问题[5-6]。为解决上述缺陷，Hochreiter在1997年提出了长短期记忆（LSTM ，Long Short-Term Memory）模型[7]。发展至今，LSTM已经在自然语言处理[8]、机器翻译[9]、轨迹预测、蛋白质结构预测[10]、音乐创作[11]等众多领域取得了显著成果。全球导航卫星系统（GNSS，Global Navigation Satellite System）监测数据可以看作一种特殊的时间序列数据，本文将LSTM模型应用于基于GNSS检测数据的铁路基础设施位移预测研究，对于保障线路安全，提升管理水平和治理能力具有重要意义。
1 监测系统及预测算法
1.1 监测系统概述
基于GNSS的铁路基础设施形变监测系统能够有效监测铁路边坡、路基、桥梁毫米级的三维形变信息，提升铁路工程监测能力。结合我国自主研发的北斗卫星导航系统不仅能够推动我国北斗产业的发展，同时，也能够在根本层面摆脱全球定位系统（GPS ，Global Positioning System）的限制，有效保障数据安全可控。
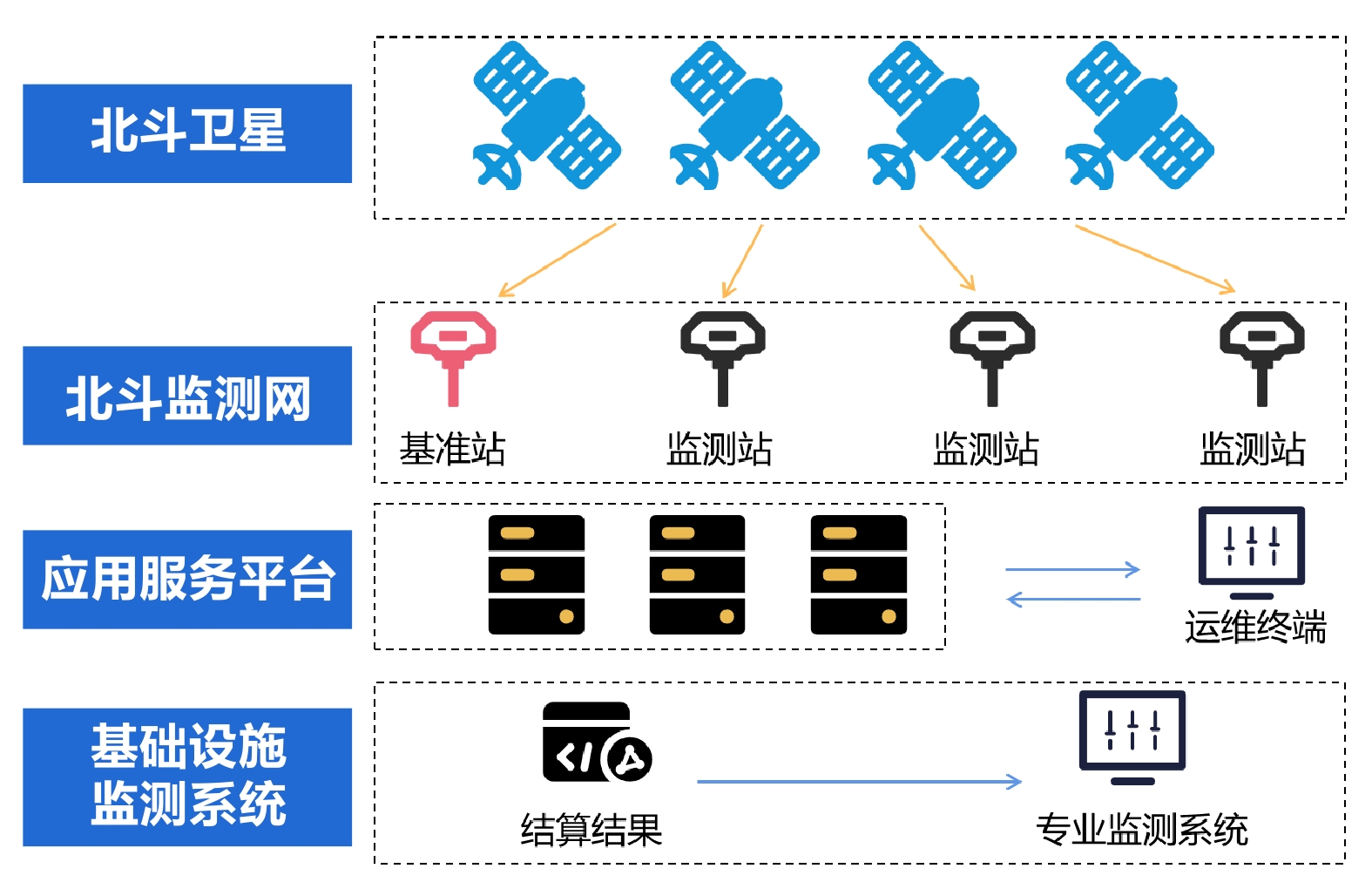
该系统由北斗卫星、北斗监测网、应用服务平台及基础设施监测系统组成，系统架构如图1所示。其中，北斗监测网由基准站与监测站共同组成，通过对北斗卫星信号的连续观测、接收、加密并传输至铁路北斗应用服务平台；应用服务平台对信号进行解密、解算并计算位移形变信息，得到的毫米级精度位移形变信息通过专业的监测应用算法，如卡尔曼滤波、形变预测等进行汇集应用，可提供专业的统计分析、预测预警信息。本文主要针对系统中用于形变预测分析的时间序列预测算法开展研究及对比实验分析。
1.2 时间序列预测算法
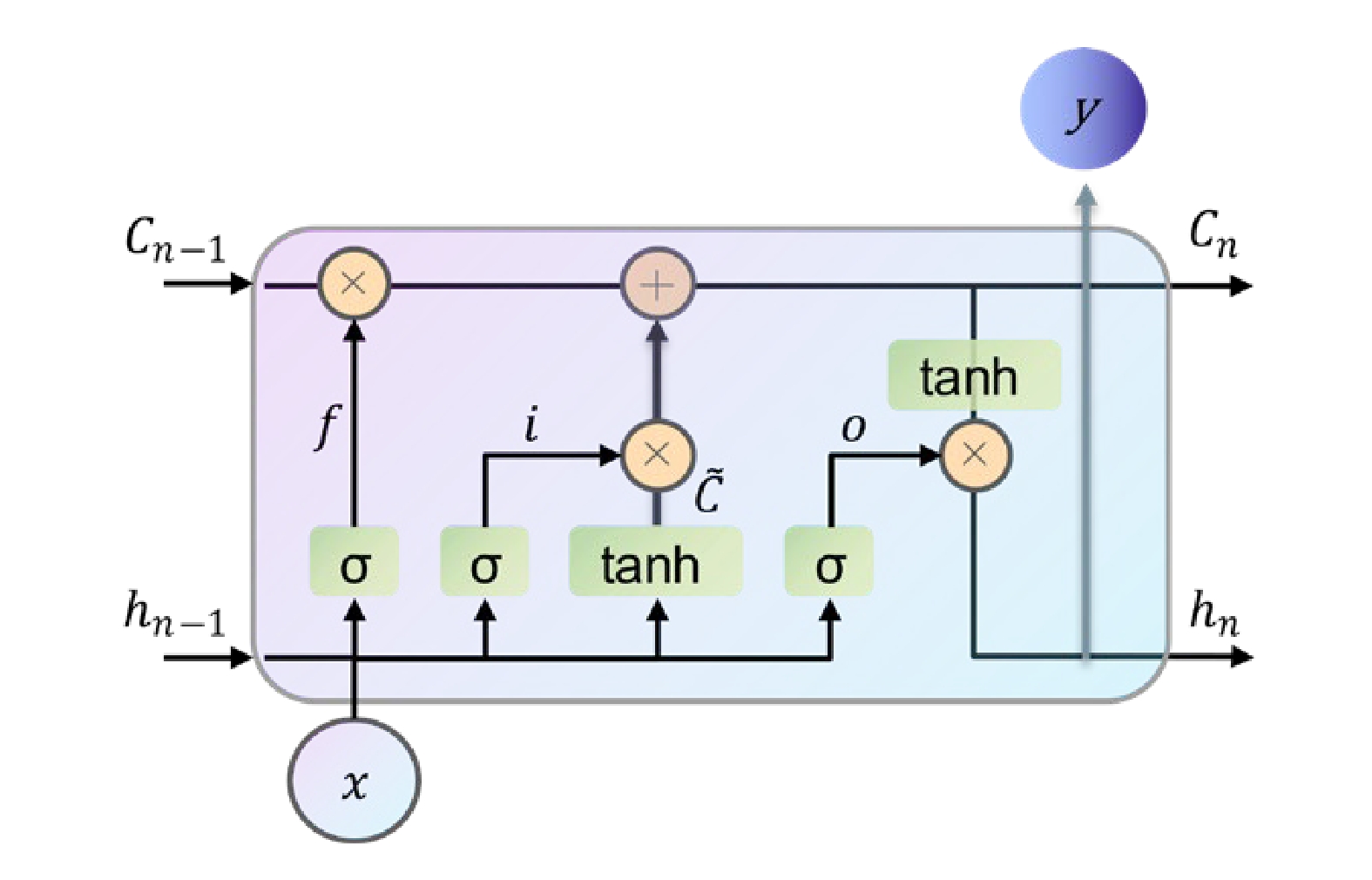
LSTM是RNN的一种改进变体，通过对常规RNN的循环单元做出改进，实现了长期依赖，解决了梯度爆炸及梯度消失的问题[6]。每一个LSTM单元通过单元状态传递信息，同时，建立通过门结构来对单元信息进行调整的数据处理模块，每一个单元的门结构包含遗忘门、输入门及输出门。目前，广泛应用的LSTM单元结构[12]如图2所示。
其中，
$ f、i、o $ 分别代表遗忘门、输入门、输出门；$ {C}_{n} $ (n=1, 2, ···, m) 表示第n个单元的状态，m为单元总数；σ、tanh分别表示Sigmoid激活函数和双曲线正切激活函数；hn表示第n个隐含层的输出；x表示当前单元的输入；y表示当前单元的输出。与RNN的循环结构不同，LSTM单元不仅数据处理过程有所增加，而且额外多出了一条单元状态信息$ {C}_{n} $ 。在单元状态信息链上，仅存在极少的线性操作，使得信息能够一直传递下去，从而保证了长距离依赖关系。（1）在LSTM单元的门结构中，输入信号最先通过的是遗忘门，即决定输入信号要遗忘掉的信息；（2）经过输入门及一个tanh网络层结构，将LSTM单元的状态信息由
$ {C}_{n-1} $ 更新至$ {C}_{n} $ ；（3）输入信号经过输出门并与经过tanh层的最新单元状态信息进行乘运算，确定单元的输出。2 数据研究
2.1 实验数据分类
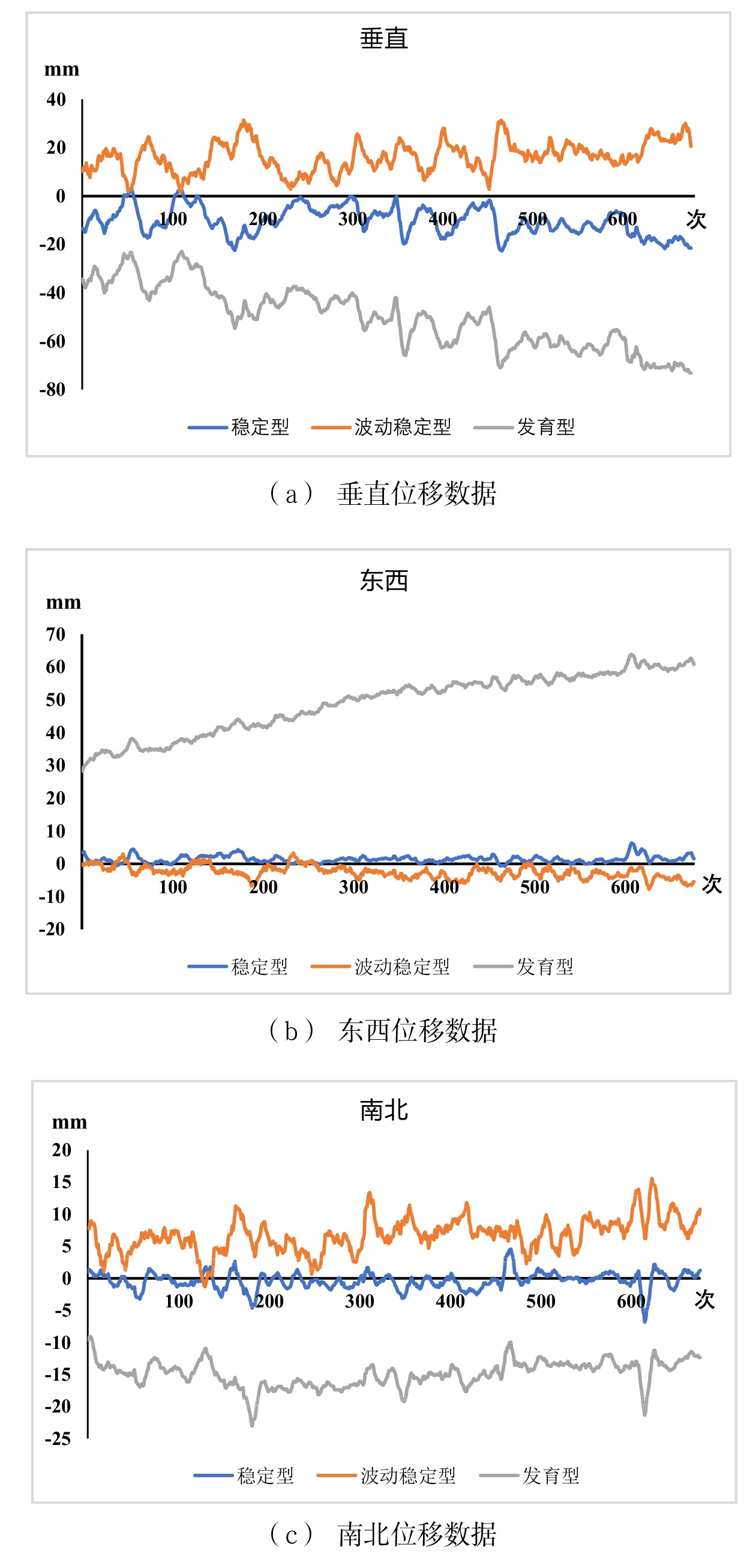
本文以边坡形变数据为研究对象，在边坡形变监测中，监测数据往往根据监测点位的不同呈现出不同的形变曲线。因受到边坡形变特征、环境因素及随机误差的影响，可将其分为3个类型：（1）发育型，该类型有形变发生，且形变量呈增长趋势；（2）稳定型，该类型无明显形变，且形变曲线较稳定；（3）波动稳定型，该类型无明显形变，但形变曲线波动较大。为了研究LSTM模型对这3种形变特征的应用效果，本文采集了一处铁路隧道仰坡2021年9月14日—10月13日，12个监测站点的GNSS三维位移监测数据，共计7832条，从中归纳选取了上述3类具有代表性的形变监测曲线开展实验，每类均包含垂直、东西、南北3个方向的形变数据，其位移曲线如图3所示。
2.2 实验数据准备
数据准备包括数据标准化和数据分割。数据标准化是数据分析中较为常见的预处理方法，无量纲化是较为常见的方式之一，主要解决同一类型数据间数值相差较大，量级不同的问题。本文所选用实验数据均为表示形变的位移数据，不同监测站的各类型数据间存在量级差异。在数据集建立之前，需对所有数据进行极值标准化，为
$$ {x}_{i}^{{'}}=({x}_{i}-{x}_{{\rm{min}}})/({x}_{{\rm{max}}}-{x}_{{\rm{min}}}) $$ (1) 其中，
$ {x}_{i}^{{'}} $ 为经过标准化后数组中的第i个值；$ {x}_{i} $ 为原始数组中的第i个值；xmin为原始数组中的最小值；xmax为原始数组中的最大值。由于每个类型的GNSS监测数据均为一维的位移数据，为了开展时间序列预测分析，我们将一维位移数据经过截取、组合，组建为m×(k+1)的二维矩阵Z。矩阵Z的每一行为一组时间序列。对于每组序列，规定前m-1个数据，作为训练数据用来学习形变特征，第m个数据作为标签，供模型计算损失值，并调整模型权值。假设有GNSS监测数据
$X=\left\{{X}_{1},{X}_{2},\cdots ,{X}_{n}\right\}$ ，相邻两组数据间的时间步长为L，则矩阵Z为 $$ \qquad\qquad\qquad {\boldsymbol{Z}}=\left[\begin{array}{cccc}{X}_{1}& {X}_{2}& \dots & {X}_{m}\\ {X}_{1+L}& {X}_{2+L}& \dots & {X}_{m+L}\\ {X}_{1+2L}& {X}_{2+2L}& \dots & {X}_{m+2L}\\ \dots & \dots & \dots & \dots \\ {X}_{1+(k-1)L}& {X}_{2+(k-1)L}& \dots & {X}_{m+(k-1)L}\\ {X}_{1+kL}& {X}_{2+kL}& \dots & {X}_{m+kL}\end{array}\right]\;\;,\;\; (1<m \leqslant m+kL\leqslant n) $$ (2) 3 实验设计
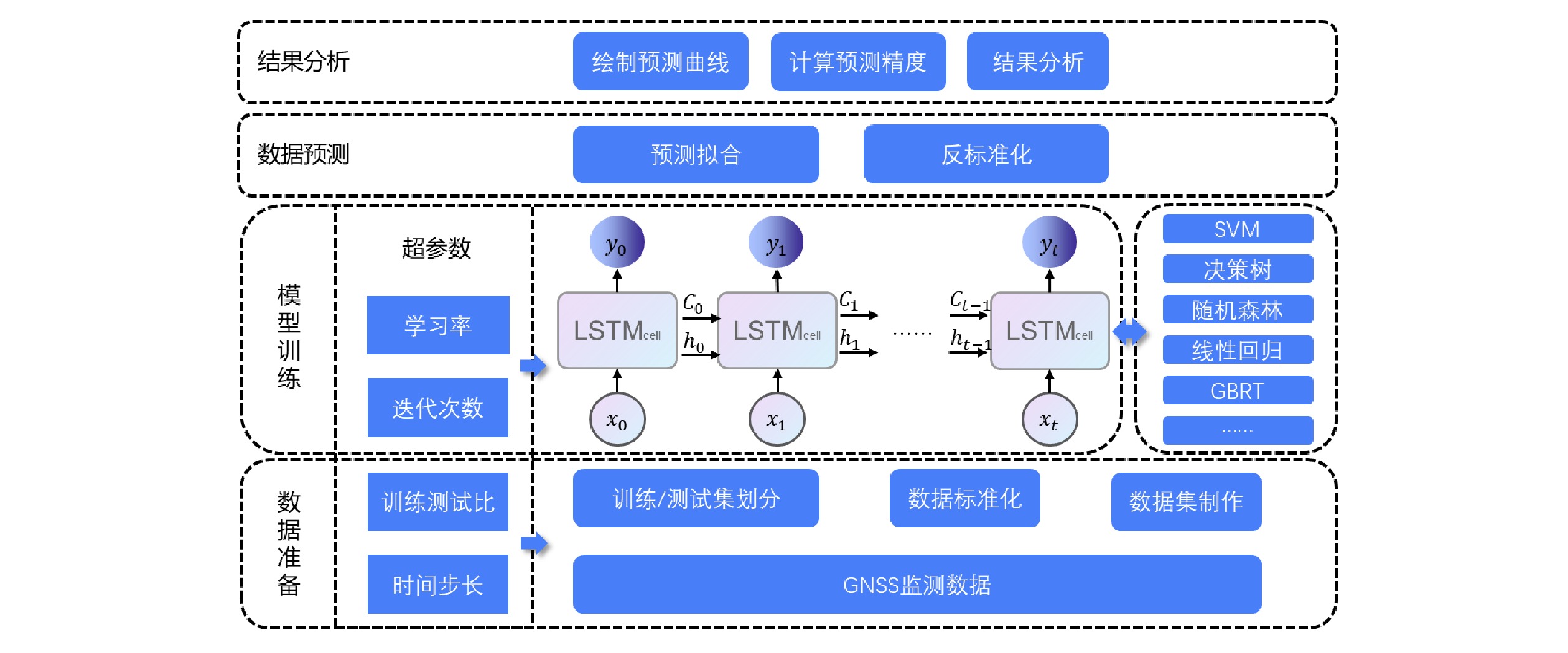
实验总体设计如图4所示，整体实验流程如下。
（1）数据准备：利用极值标准化法进行数据标准化，3种形变类型的3个方向维度的9组形变数据分别根据设定的时间步长（L=1）制作二维数据矩阵，并采用7:3的训练测试比进行训练集、测试集的划分，制定实验数据集。
（2）模型训练：为了进一步研究LSTM模型隐藏层数对预测精度的影响，本文分别定义了包含8个隐藏层的LSTM8和包含12个隐藏层的LSTM12。设定学习率为0.01，迭代次数为500，按照划分好的数据集开展多模型对比实验，对比模型均选用常见的回归模型。
（3）数据预测：通过对比训练完成的模型对测试数据开展预测，并对预测结果进行反标准化，得到真实量纲的预测形变值。
（4）结果分析：将结果与真实数据对比，绘制形变预测曲线，并计算均方根误差（RMSE ，Root Mean Square Error）、平均绝对误差（MAE ，Mean Absolute Error）指标开展精度评价，分析各模型的预测效果。
4 实验分析
4.1 精度评估
为进一步检验LSTM模型的预测效果，本文采用常见的时间序列预测模型进行对比实验，选用的模型有线性回归（Linear）、决策树回归（DT ，Decision Tree）、支持向量机（SVM ，Support Vector Machine）、随机森林（RF ，Random Forest）回归、迭代决策树（GBRT ，Gradient Boost Regression Tree）等。
为量化模型训练、预测效果，本文选定训练时间、RMSE及MAE 3个指标对模型性能进行评价，RMSE、MAE的计算分别表示为
$$ RMSE=\sqrt{{\sum }_{t=1}^{N}{（{y}_{t}-{x}_{t}）}^{2}/N} $$ (3) $$ MAE=1/N\cdot {\sum }_{t=1}^{N}\left|{y}_{t}-{x}_{t}\right| $$ (4) 其中，N为数据样本数；
$ {y}_{t} $ 表示t时刻的形变位移预测值；$ {x}_{t} $ 表示t时刻的形变位移真实值。4.2 发育型实验及分析
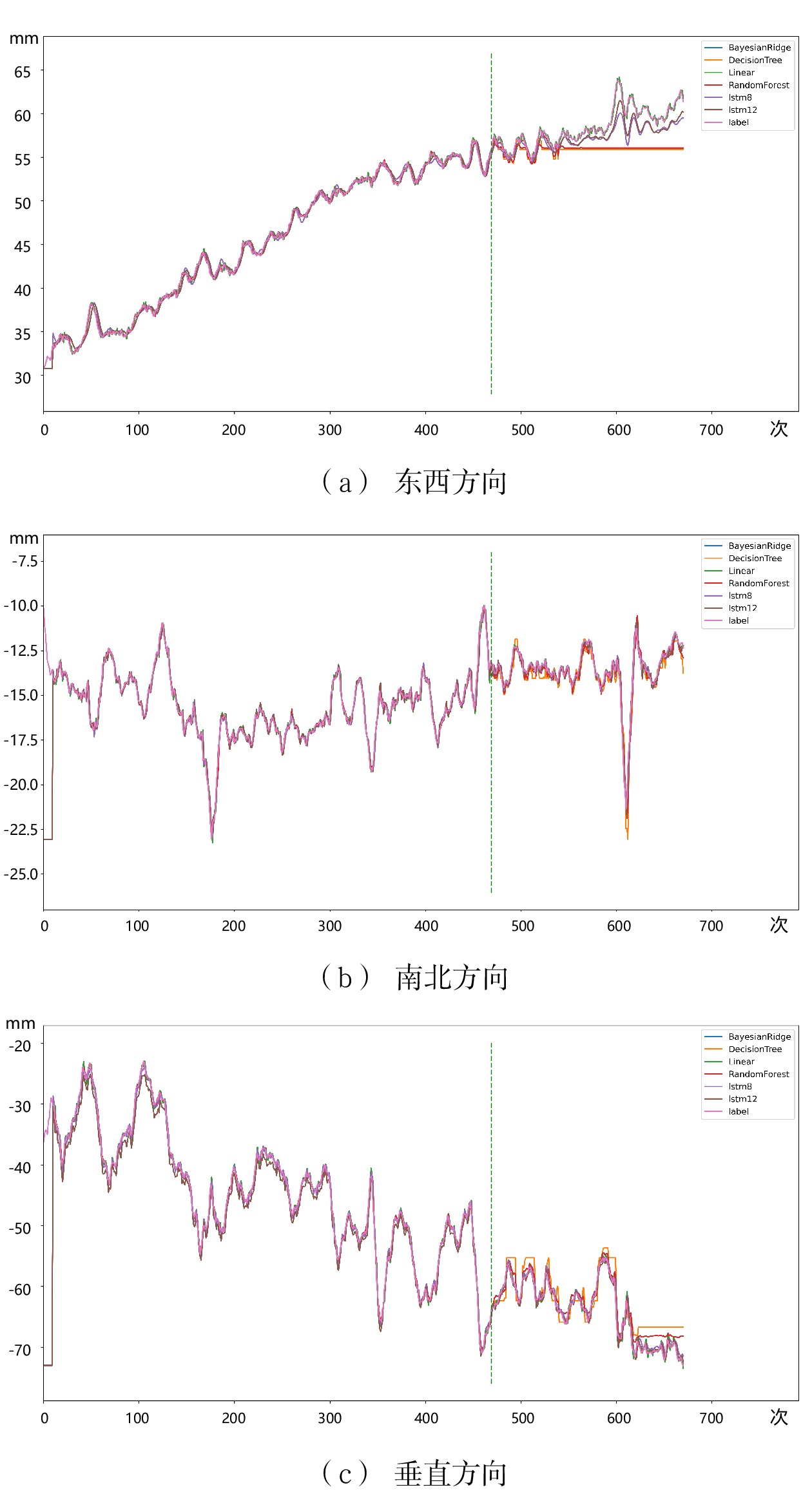
对于发育型监测曲线，其形变量随时间变化而累计，形变数据主要受监测区域的自身形变特性影响。对该类型数据开展多模型对比实验，各模型精度指标如表1所示。观察表1可知，Linear模型具有更好的指标值，拟合特性及时间效率均较好。LSTM模型用时最高，整体拟合效果略差于Linear模型。
表 1 发育型监测数据预测精度指标东西 南北 垂直 Time RMSE MAE Time RMSE MAE Time RMSE MAE DT 0.04 0.101 0.083 0.05 0.045 0.033 0.08 0.044 0.034 Linear 0.06 0.011 0.008 0.06 0.026 0.019 0.08 0.017 0.013 SVM 0.08 0.240 0.212 0.08 0.073 0.042 0.017 0.099 0.067 RF 0.11 0.099 0.079 0.12 0.037 0.026 0.10 0.032 0.024 GBRT 0.16 0.103 0.083 0.16 0.038 0.025 0.08 0.033 0.026 ET 0.19 0.102 0.084 0.21 0.045 0.033 0.10 0.051 0.042 ARD 0.21 0.011 0.008 0.23 0.026 0.019 0.44 0.017 0.013 Byesian 0.23 0.011 0.008 0.25 0.026 0.019 0.08 0.017 0.013 TheilSen 0.25 0.011 0.008 0.27 0.026 0.019 0.12 0.016 0.012 RANSAC 0.28 0.011 0.008 0.29 0.026 0.019 0.28 0.017 0.012 LSTM8 2.55 0.030 0.023 2.55 0.025 0.017 2.55 0.018 0.013 LSTM12 2.60 0.035 0.026 2.55 0.027 0.019 2.60 0.021 0.015 针对表中各类模型的指标，重点选取了Byesian、DT、Linear、RF、LSTM8及LSTM12进行预测曲线制图，并与实际形变曲线（“label”曲线）进行对比，如图5所示。结果显示，对于表现出了显著形变趋势的数据样本（如该组监测数据的东西、垂直方向监测数据），线性模型具有较好的预测拟合效果。DT、RF等模型都仅在训练过程中（绿线左侧）表现出了较好的拟合特性，在测试数据部分（绿线右侧）表现较差。虽然LSTM模型在两个位移变化趋势明显的数据（东西、垂直方向）中预测效果略差于线性模型，但整体来看3个方向的位移预测均有较好表现。此外，可以发现针对该类型数据，LSTM8预测效果略好于LSTM12。
4.3 稳定型实验及分析
对于稳定型监测曲线，其整体形变趋势不随时间变化而变化，且曲线波动较小，形变数据整体受无序的观测误差影响。对该类型的GNSS监测数据开展多模型对比实验，模型精度指标如表2所示。可以发现，虽然LSTM模型依旧花费了最高的时间成本，但其在该类监测数据的3个方位位移预测拟合上均取得了最好的结果，而其他对比模型的预测拟合效果均较差。
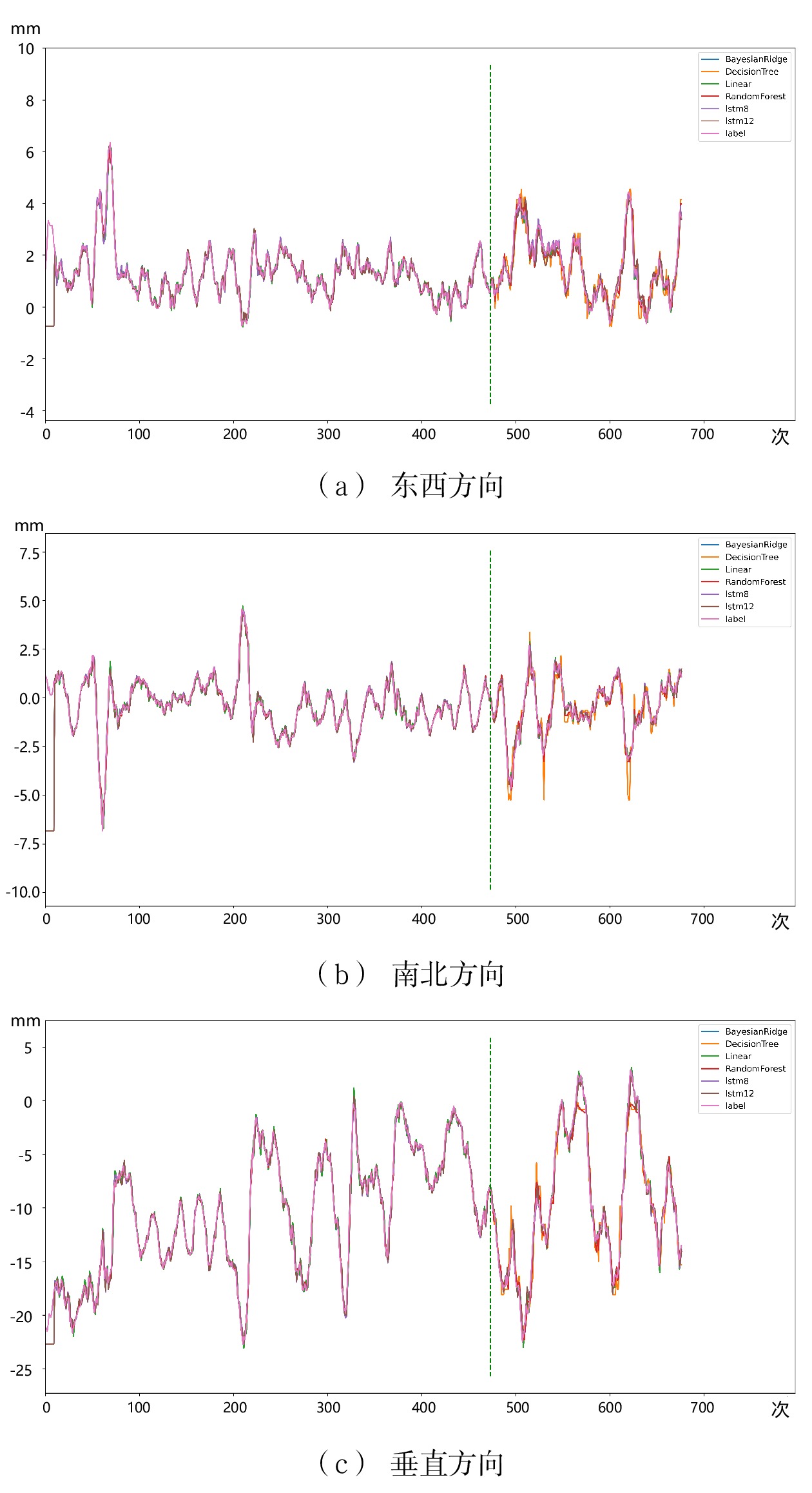
表 2 稳定型监测数据预测精度指标东西 南北 垂直 Time RMSE MAE Time RMSE MAE Time RMSE MAE DT 0.04 0.060 0.048 0.05 0.048 0.035 0.04 0.052 0.042 Linear 0.06 0.041 0.033 0.06 0.030 0.023 0.06 0.031 0.024 SVM 0.07 0.068 0.053 0.08 0.053 0.040 0.07 0.091 0.066 RF 0.11 0.049 0.039 0.12 0.034 0.028 0.10 0.045 0.034 GBRT 0.14 0.048 0.038 0.17 0.035 0.028 0.14 0.046 0.035 ET 0.17 0.066 0.052 0.21 0.055 0.041 0.17 0.056 0.045 ARD 0.19 0.041 0.033 0.23 0.030 0.023 0.19 0.031 0.025 Byesian 0.20 0.041 0.033 0.25 0.030 0.023 0.21 0.031 0.024 TheilSen 0.22 0.047 0.039 0.27 0.031 0.024 0.22 0.031 0.025 RANSAC 0.23 0.046 0.038 0.29 0.031 0.024 0.24 0.031 0.024 LSTM8 2.55 0.038 0.031 2.58 0.034 0.027 2.59 0.031 0.024 LSTM12 2.53 0.040 0.032 2.60 0.027 0.021 2.60 0.030 0.023 对4.2中选取的6个模型的预测结果进行制图分析，如图6所示。结果显示，该类型监测数据整体呈现平稳波动，如东西、南北方向。对于存在相对波动较大的垂直方向，LSTM模型在预测位移时也表现出了较好的鲁棒性。LSTM8取得了东西方向预测指标的最佳，当隐藏层数增加到12后，南北、垂直方向预测精度得到了提升，东西方向却有所下降，由此可见模型构建参数对于预测精度存在较大影响。
4.4 波动稳定型实验及分析
对于波动稳定型监测曲线，其在整体的位移趋势上保持稳定，但在较小的时间范围内存在一定的形变特征，这主要是受环境如温度、降雨等因素影响产生的，针对该类监测数据开展多模型对比实验，模型精度指标如表3所示。通过表中的精度指标对比可以发现， LSTM模型的拟合预测结果优于其他10个时间序列预测模型，说明在GNSS监测数据的预测上，LSTM相较于其他模型更具有优势。对于时间成本问题，考虑整体时间成本仍然处于较低水平，同时，在应用过程中的计算资源要远大于实验环境所能提供的计算资源，因此可忽略不计。
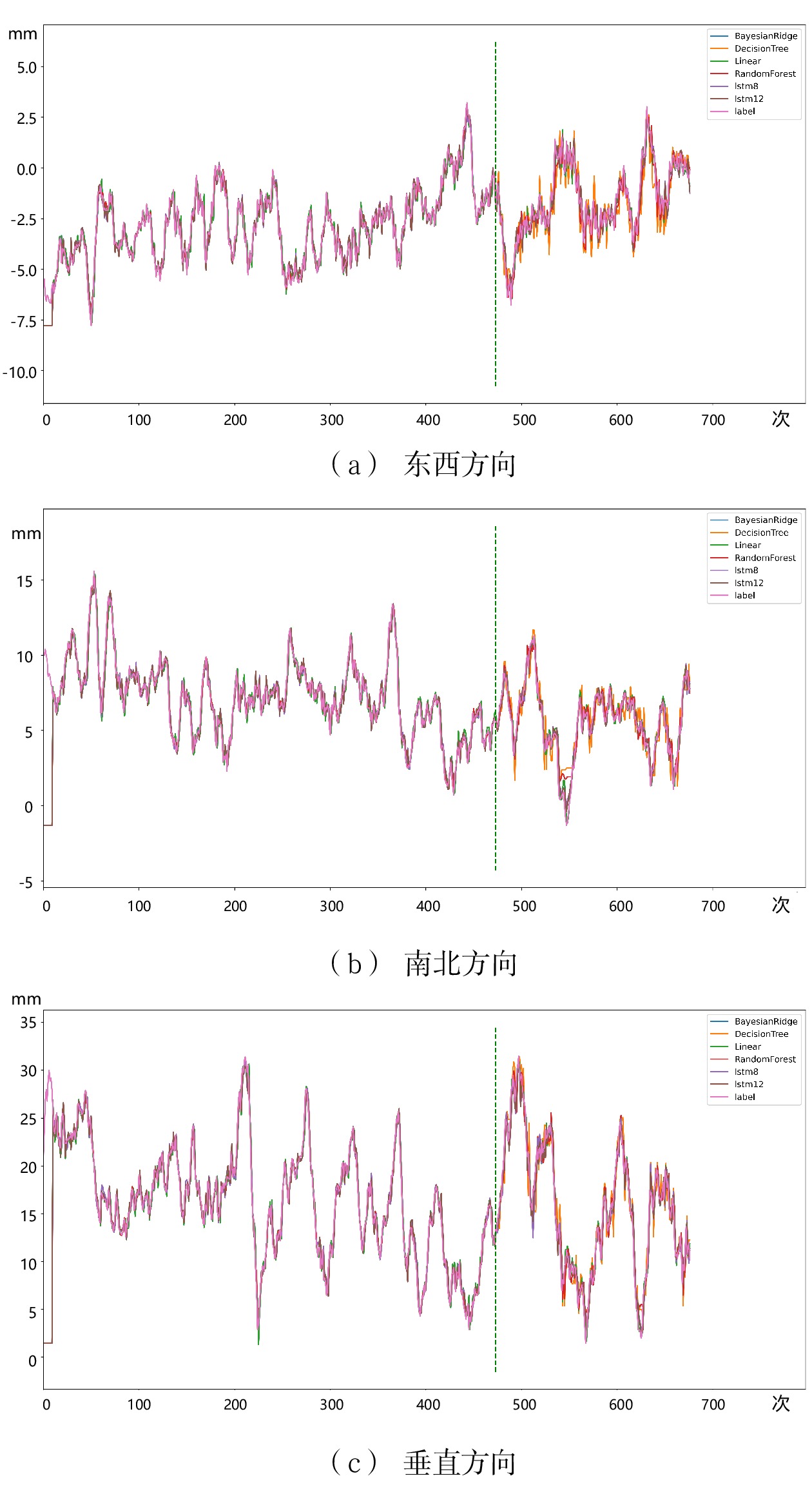
表 3 波动稳定型监测数据预测精度指标东西 南北 垂直 Time RMSE MAE Time RMSE MAE Time RMSE MAE DT 0.04 0.084 0.067 0.05 0.067 0.053 0.04 0.067 0.056 Linear 0.06 0.049 0.038 0.08 0.040 0.031 0.06 0.048 0.039 SVM 0.08 0.064 0.047 0.10 0.080 0.051 0.08 0.066 0.053 RF 0.11 0.060 0.047 0.13 0.050 0.039 0.11 0.054 0.044 GBRT 0.15 0.054 0.043 0.17 0.052 0.040 0.16 0.055 0.043 ET 0.18 0.080 0.064 0.21 0.073 0.056 0.19 0.078 0.064 ARD 0.19 0.049 0.038 0.22 0.040 0.031 0.20 0.047 0.039 Byesian 0.21 0.049 0.037 0.24 0.040 0.031 0.22 0.048 0.039 TheilSen 0.22 0.052 0.040 0.26 0.042 0.033 0.24 0.049 0.040 RANSAC 0.24 0.052 0.040 0.27 0.041 0.031 0.25 0.051 0.041 LSTM8 2.68 0.041 0.032 2.46 0.036 0.028 2.76 0.046 0.037 LSTM12 2.60 0.043 0.034 2.62 0.035 0.026 2.65 0.048 0.038 同样对前述6个模型的预测拟合结果进行制图分析，如图7所示。
结果显示，实验所采用的对比实验模型均存在训练数据预测效果与测试数据预测效果相差较大的问题，模型泛化性能差，难以适应复杂序列预测任务。而LSTM模型的拟合效果要优于其他对比模型，其学习效果更好、更能够适应复杂的任务需求。
5 结束语
随着铁路建设的快速发展，实现铁路线路监测自动预警对于线路安全保障工作具有重要意义。在本文实验中，LSTM模型取得了最佳的预测结果，在3个常见的监测数据类型的形变预测中都有较好的表现，是一种鲁棒性强、精度可靠的预测模型，但在时间效率层面，LSTM要略差于线性模型。考虑到LSTM的主要时间成本花费在前期训练过程，训练出一个泛化性强、具有迁移能力的模型将会是有效缩短时间成本的重要研究方向。
-
表 1 发育型监测数据预测精度指标
东西 南北 垂直 Time RMSE MAE Time RMSE MAE Time RMSE MAE DT 0.04 0.101 0.083 0.05 0.045 0.033 0.08 0.044 0.034 Linear 0.06 0.011 0.008 0.06 0.026 0.019 0.08 0.017 0.013 SVM 0.08 0.240 0.212 0.08 0.073 0.042 0.017 0.099 0.067 RF 0.11 0.099 0.079 0.12 0.037 0.026 0.10 0.032 0.024 GBRT 0.16 0.103 0.083 0.16 0.038 0.025 0.08 0.033 0.026 ET 0.19 0.102 0.084 0.21 0.045 0.033 0.10 0.051 0.042 ARD 0.21 0.011 0.008 0.23 0.026 0.019 0.44 0.017 0.013 Byesian 0.23 0.011 0.008 0.25 0.026 0.019 0.08 0.017 0.013 TheilSen 0.25 0.011 0.008 0.27 0.026 0.019 0.12 0.016 0.012 RANSAC 0.28 0.011 0.008 0.29 0.026 0.019 0.28 0.017 0.012 LSTM8 2.55 0.030 0.023 2.55 0.025 0.017 2.55 0.018 0.013 LSTM12 2.60 0.035 0.026 2.55 0.027 0.019 2.60 0.021 0.015 
下载: 导出CSV
表 2 稳定型监测数据预测精度指标
东西 南北 垂直 Time RMSE MAE Time RMSE MAE Time RMSE MAE DT 0.04 0.060 0.048 0.05 0.048 0.035 0.04 0.052 0.042 Linear 0.06 0.041 0.033 0.06 0.030 0.023 0.06 0.031 0.024 SVM 0.07 0.068 0.053 0.08 0.053 0.040 0.07 0.091 0.066 RF 0.11 0.049 0.039 0.12 0.034 0.028 0.10 0.045 0.034 GBRT 0.14 0.048 0.038 0.17 0.035 0.028 0.14 0.046 0.035 ET 0.17 0.066 0.052 0.21 0.055 0.041 0.17 0.056 0.045 ARD 0.19 0.041 0.033 0.23 0.030 0.023 0.19 0.031 0.025 Byesian 0.20 0.041 0.033 0.25 0.030 0.023 0.21 0.031 0.024 TheilSen 0.22 0.047 0.039 0.27 0.031 0.024 0.22 0.031 0.025 RANSAC 0.23 0.046 0.038 0.29 0.031 0.024 0.24 0.031 0.024 LSTM8 2.55 0.038 0.031 2.58 0.034 0.027 2.59 0.031 0.024 LSTM12 2.53 0.040 0.032 2.60 0.027 0.021 2.60 0.030 0.023
下载: 导出CSV
表 3 波动稳定型监测数据预测精度指标
东西 南北 垂直 Time RMSE MAE Time RMSE MAE Time RMSE MAE DT 0.04 0.084 0.067 0.05 0.067 0.053 0.04 0.067 0.056 Linear 0.06 0.049 0.038 0.08 0.040 0.031 0.06 0.048 0.039 SVM 0.08 0.064 0.047 0.10 0.080 0.051 0.08 0.066 0.053 RF 0.11 0.060 0.047 0.13 0.050 0.039 0.11 0.054 0.044 GBRT 0.15 0.054 0.043 0.17 0.052 0.040 0.16 0.055 0.043 ET 0.18 0.080 0.064 0.21 0.073 0.056 0.19 0.078 0.064 ARD 0.19 0.049 0.038 0.22 0.040 0.031 0.20 0.047 0.039 Byesian 0.21 0.049 0.037 0.24 0.040 0.031 0.22 0.048 0.039 TheilSen 0.22 0.052 0.040 0.26 0.042 0.033 0.24 0.049 0.040 RANSAC 0.24 0.052 0.040 0.27 0.041 0.031 0.25 0.051 0.041 LSTM8 2.68 0.041 0.032 2.46 0.036 0.028 2.76 0.046 0.037 LSTM12 2.60 0.043 0.034 2.62 0.035 0.026 2.65 0.048 0.038
下载: 导出CSV
-
[1] 雷绍兰,孙才新,周 湶. 电力短期负荷的多变量时间序列线性回归预测方法研究 [J]. 中国电机工程学报,2006(2):25-29. DOI: 10.3321/j.issn:0258-8013.2006.02.005 [2] 刘 静,关 伟. 交通流预测方法综述 [J]. 公路交通科技,2004(3):82-85. DOI: 10.3969/j.issn.1002-0268.2004.03.022 [3] 杨秀媛,肖 洋,陈树勇. 风电场风速和发电功率预测研究 [J]. 中国电机工程学报,2005(11):1-5. DOI: 10.3321/j.issn:0258-8013.2005.11.001 [4] CHO K, VAN MERRIëNBOER B, GULCEHRE C, et al. Learning phrase representations using RNN encoder-decoder for statistical machine translation [J]. arXiv preprint arXiv:, 1406, 1078: 2014.
[5] WERBOS P J. Generalization of backpropagation with application to a recurrent gas market model [J]. Neural networks, 1988, 1(4): 339-356. DOI: 10.1016/0893-6080(88)90007-X
[6] HOCHREITER S. Untersuchungen zu dynamischen neuronalen Netzen [J]. Diploma, Technische Universität München, 1991, 91(1).
[7] HOCHREITER S, SCHMIDHUBER J. Long short-term memory [J]. Neural computation, 1997, 9(8): 1735-1780. DOI: 10.1162/neco.1997.9.8.1735
[8] GERS F A, SCHMIDHUBER J. LSTM recurrent networks learn simple context-free and context-sensitive languages [J]. IEEE transactions on neural networks, 2001, 12(6): 1333-1340. DOI: 10.1109/72.963769
[9] Srivastava N , Mansimov E , Salakhutdinov R . Unsupervised Learning of Video Representations using LSTMs[J]. JMLR. org, 2015.
[10] HANSON J, YANG Y, PALIWAL K, et al. Improving protein disorder prediction by deep bidirectional long short-term memory recurrent neural networks [J]. Bioinformatics, 2017, 33(5): 685-692.
[11] ECK D, LAPALME J. Learning musical structure directly from sequences of music [J]. University of Montreal, Department of Computer Science, 2008.
[12] GREFF K, SRIVASTAVA R K, KOUTNíK J, et al. LSTM: A search space odyssey [J]. IEEE transactions on neural networks and learning systems, 2016, 28(10): 2222-2232.
-
期刊类型引用(6)
1. 王媛，李俊达，鸭磊，吴全才，吕彦颉，王慧杰. 基于麻雀搜索算法优化长短期记忆网络模型的充电桩零部件采购需求预测. 云南电力技术. 2025(01): 61-67 . 
百度学术
2. 刘亿，李平，封博卿，潘佩芬，王雪影. 基于北斗技术的铁路工务基础设施监测应用总体框架研究. 中国铁路. 2025(03): 17-26 . 百度学术
3. 燕学博，曹世鑫. 基于CNN-LSTM-Attention组合模型对我国货运量时序预测对比. 物流科技. 2024(14): 5-9 . 百度学术
4. 马昆，周子健，朱攀峰. 基于北斗定位技术的铁路基础设施监测系统设计与应用. 铁路计算机应用. 2023(01): 40-45 . 本站查看
5. 赵一颖，姜志威，孙永辉，苏东徽. 高铁数字化运维中的北斗创新应用. 铁道标准设计. 2023(10): 201-207 . 百度学术
6. 刘亿，李平，封博卿，蒋丽丽，李聪旭，王虎，杨美皓. 基于分数阶理论的铁路基础设施形变监测数据分析与挖掘. 导航定位与授时. 2023(04): 24-36 . 百度学术
其他类型引用(1)
计量
- 文章访问数: 181
- HTML全文浏览量: 89
- PDF下载量: 35
- 被引次数: 7
