Research on passenger flow forecast for railway passenger station based on XGBoost in post-pandemic era
-
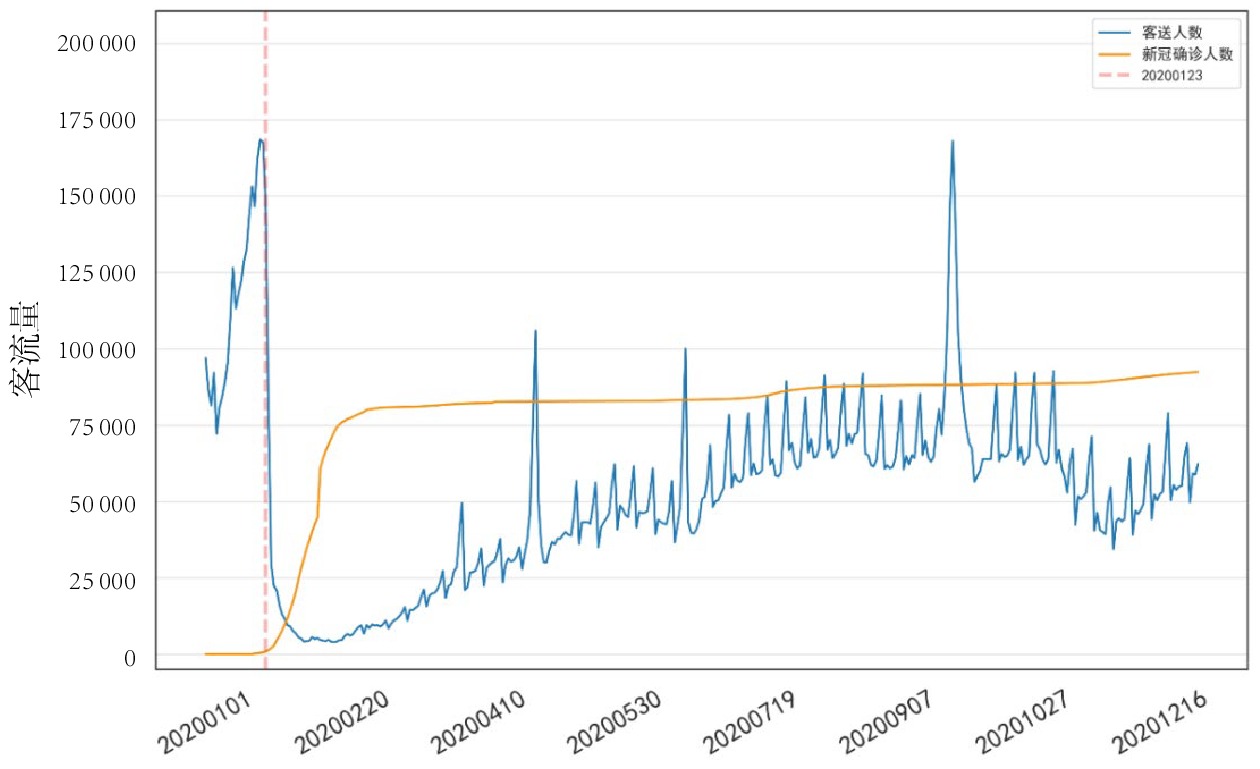
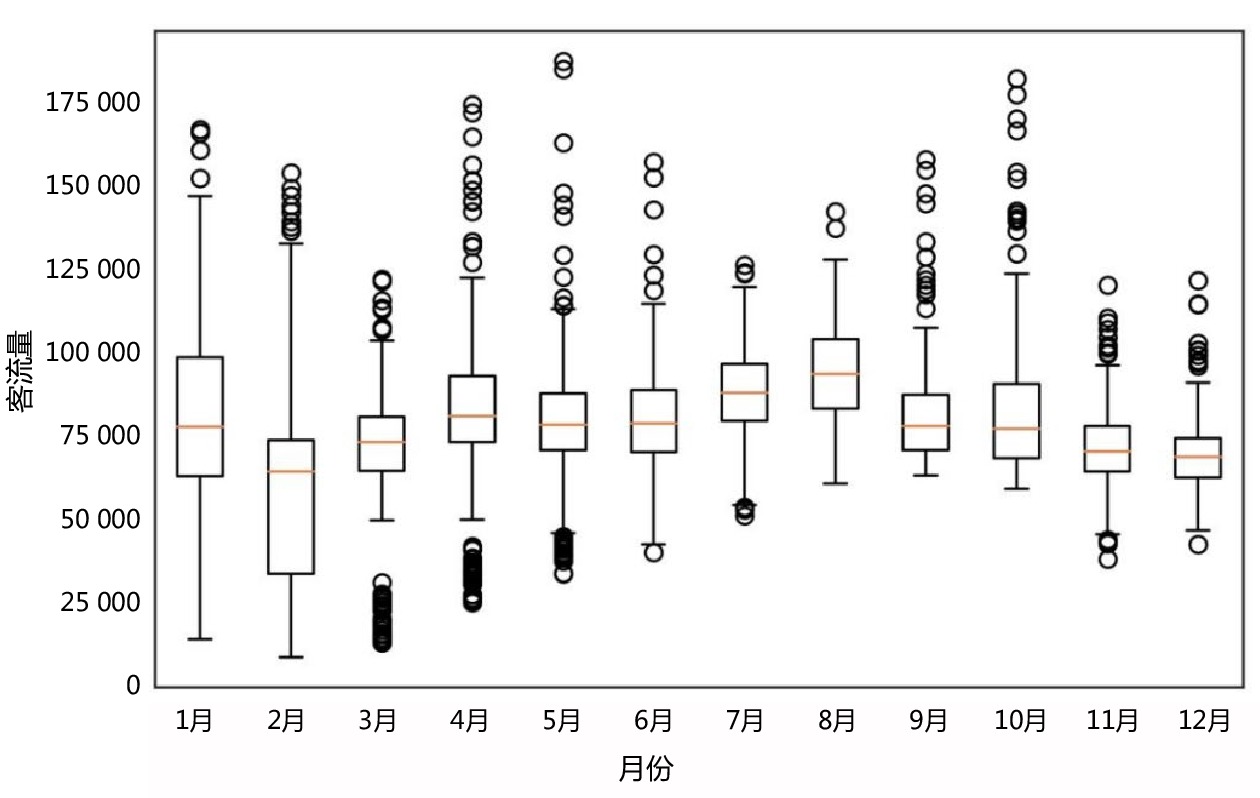
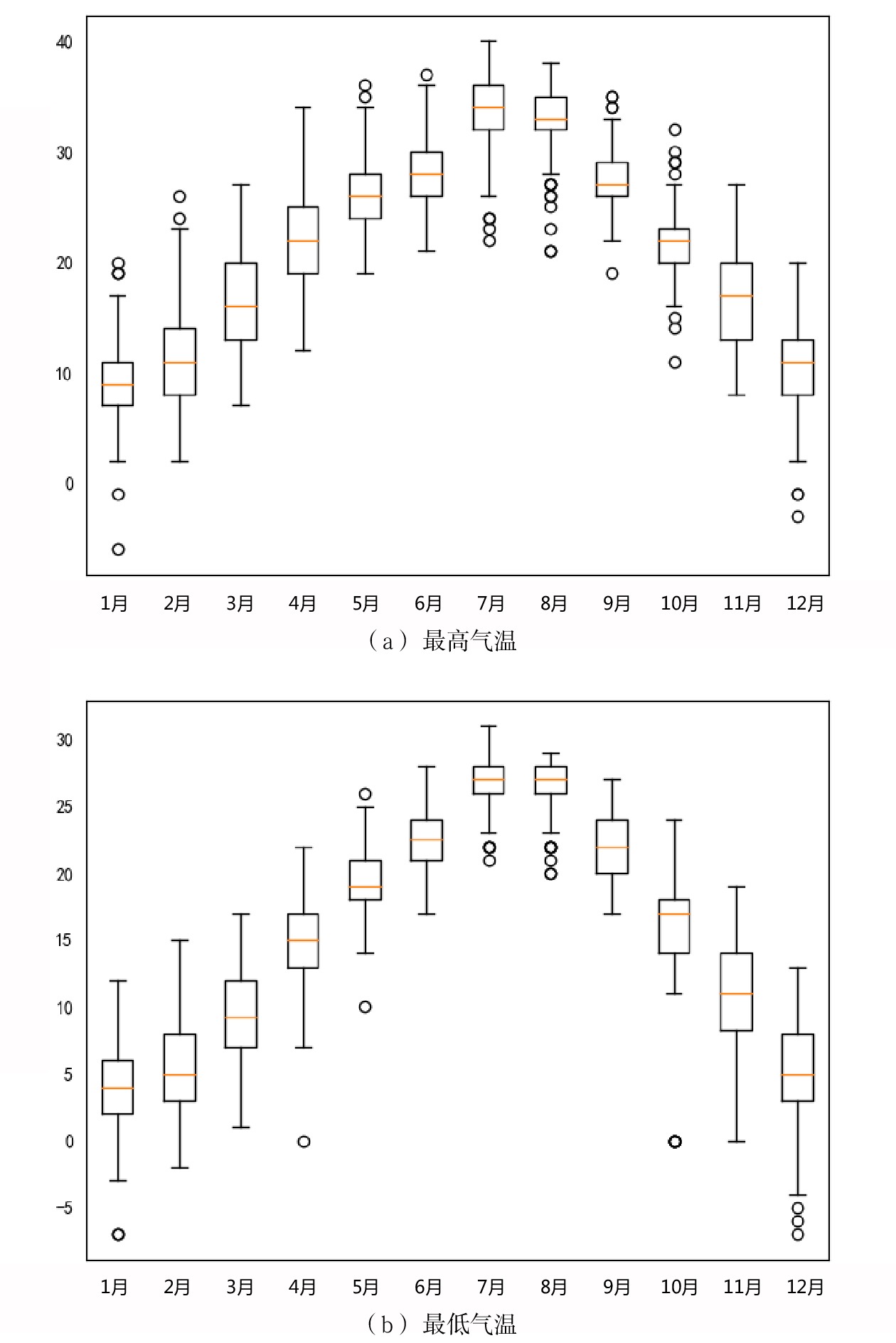
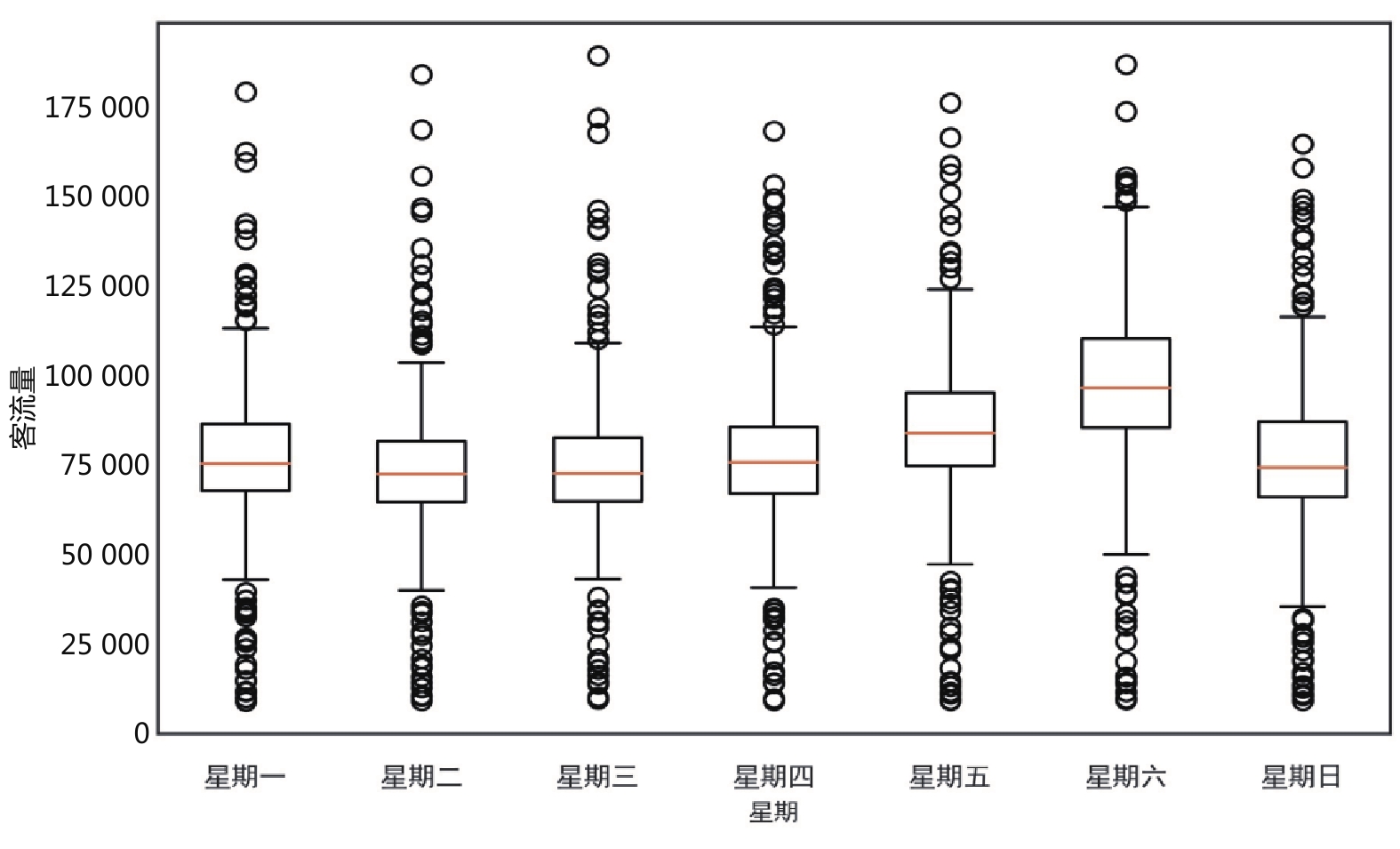
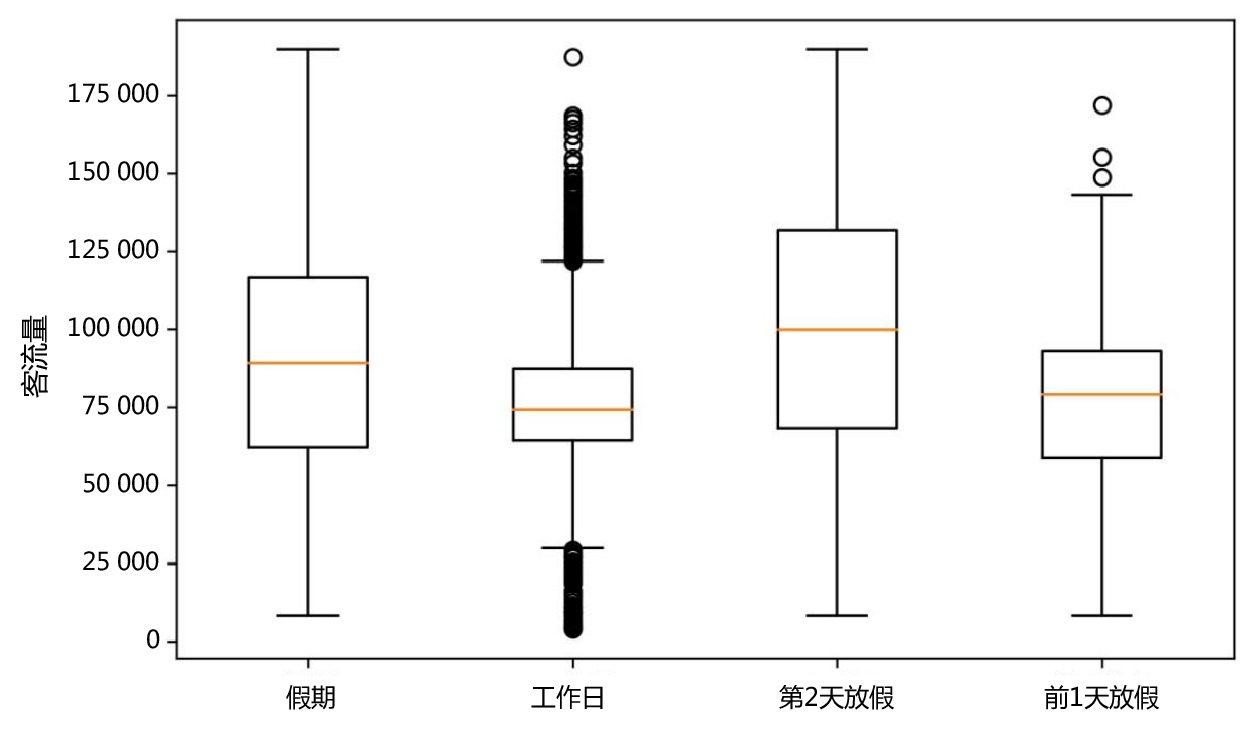
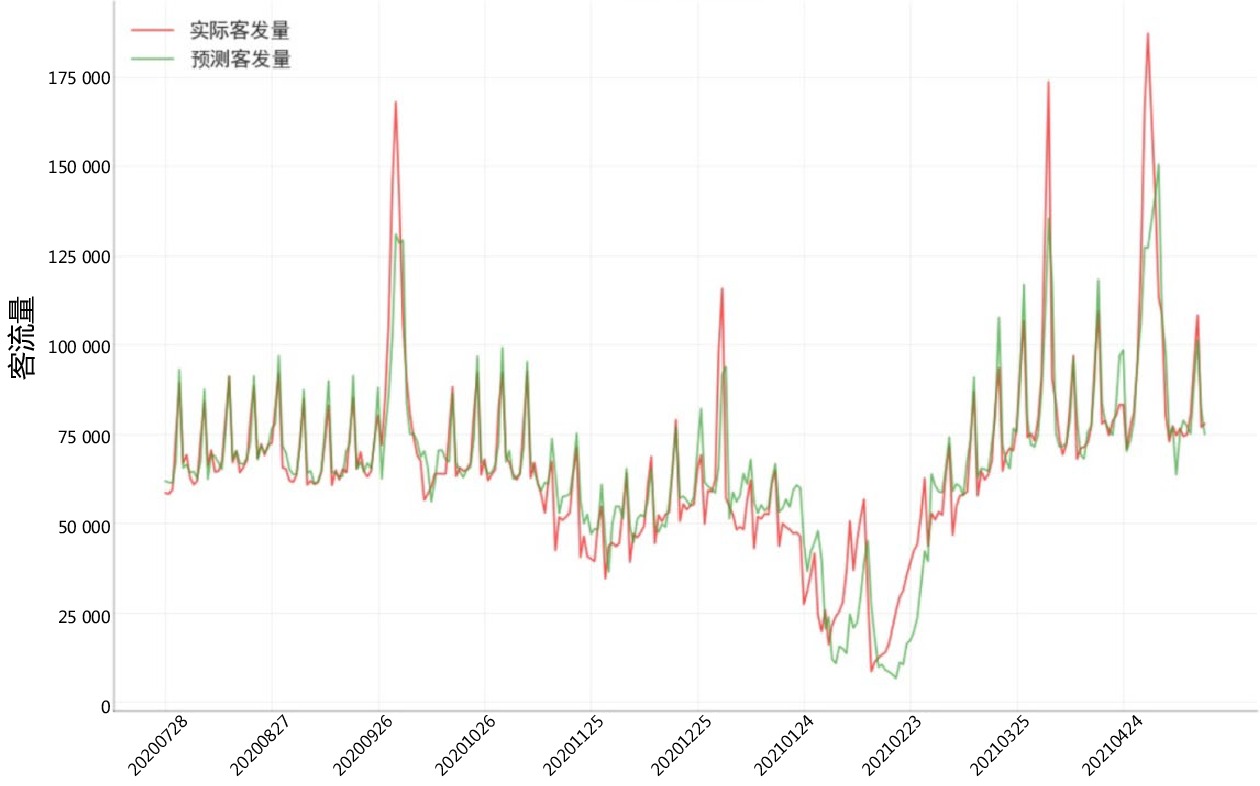
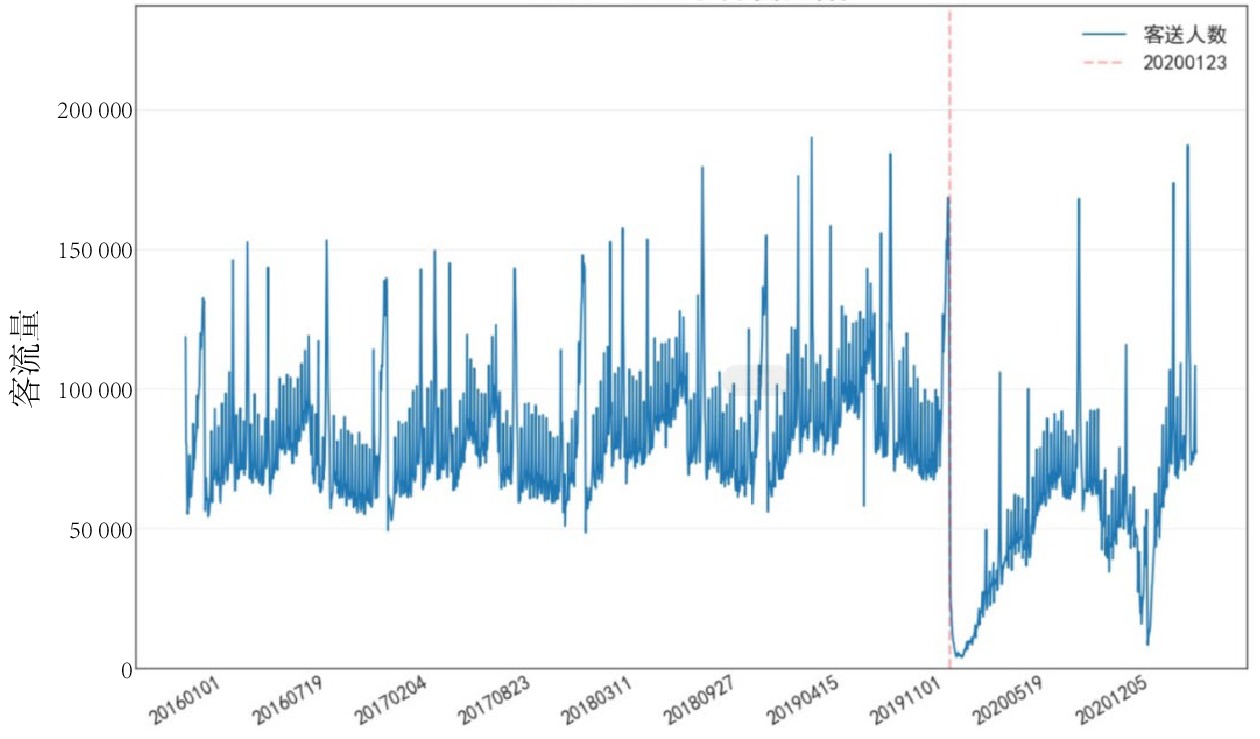
摘要: 进入“后疫情时期”，铁路客流正逐步回升，但呈现较大波动，面对铁路提质增效的任务，准确预测客流量愈发重要。文章采用极端梯度提升（XGBoost，eXtreme Gradient Boosting）模型，以新冠肺炎疫情、天气和日期属性作为影响因素，选取上海站2016年1月1日—2020年7月27日客流量数据作为训练集和验证集，利用5折交叉验证和网格搜索（Grid Search）得到最优参数，并对上海站2020年7月28日—2021年5月17日的客流量进行预测，预测拟合度
$ {R}^{2} $ 为0.812，总体预测效果较好。Abstract: Entering the post-pandemic era, railway passenger flow is gradually rising, but there is a large fluctuation. Facing the task of improving the quality and operation efficiency of railway, accurate prediction of passenger flow is becoming more and more important. In this paper, XGBoost model was adopted for passenger flow forecast with COVID-19 pandemic, weather, and date attributes as influencing factors. Meanwhile, passenger flow data of Shanghai Railway Station from January 1, 2016 to July 27, 2020 were selected as training set and validation set and the optimal parameters of the XGBoost-based passenger flow forecast model were obtained by using 5-fold cross-validation and Grid Search. Then, the passenger flow of Shanghai Railway Station from July 28, 2020 to May 17, 2021 was predicted using this model. The result of the prediction attained a fitting degree of 0.812, indicating that the overall prediction effect is good. -
铁路客运站客流量是铁路行车组织中制定开行方案、编制列车运行图和完成客流输送的重要依据。准确预测大型客运站的客流量，有利于铁路运输部门根据车站客流变化趋势和客流周期性特征，制定有效、经济的开行方案，编制适应旅客出行需求的列车运行图，实现铁路大型客运站客流的高效、安全、及时输送。
目前，国内关于铁路客流预测方法已有不少研究，这些方法针对的预测对象各有不同。李丽辉[1]等人运用基于随机森林回归算法，建立高速铁路短期客流预测模型，对京沪高速铁路2015年7、8月份的下行客流进行预测，预测精度高达0.92；豆飞[2]等人建立铁路客运专线的模糊K近邻（FKNN，fuzzy k-nearest neighbor）预测模型，并利用2011—2012年中3个月的短期客流数据，验证预测模型的有效性；段然[3]等人针对节假日与非节假日2种类型客流，分别采用波动系数模型及SARIMA模型，对某铁路车站的客流量进行预测。
本文采用支持向量回归（SVR，Support Vector Regression）方法，以汉口枢纽站为例，研究将支持向量回归方法应用于预测铁路大型客运站客流量的效果。
1 支持向量回归模型简介
支持向量机是一种二分类模型，其本质是在多维空间中找到一个超平面（例如二维空间中的直线和三维空间中的平面），来对需要研究的样本进行分割，使得分割后的各子样本间隔最大化，转化为凸规划问题进行求解。对于回归问题，可引入支持向量机模型，对给定样本
$D = \{ ({x_1},{y_1}),({x_2},{y_2}),\cdots,({x_n},{y_n})\}$ ，求得一个回归模型$F(x) = {\omega ^T}x + b$ ，$\omega $ 为决策面的法向量，$b$ 为决策面的位置，使得预测值$F(x)$ 与真实值${y_n}$ 之间尽可能接近。与传统回归模型不同，支持向量回归引入“损失带”的概念[4-5]，设置一个可以接受的损失范围，只要真实误差不超过这一损失范围，就不计入误差。如图1所示，设真实值为${\rm{F}}(x)$ ，设置一个不敏感损失（insensitive error，记为$ \epsilon $ ），当样本值落在区间[$F(x)-\epsilon $ ,$F(x)+\epsilon $ ]之外时，其误差才被计入。按照统计理论，在分类或回归预测时，可能存在经验风险和结构风险，通过将其最小化的线性组合以确定其模型参数，可以得到SVR的目标及规划如式（1）[6]：
$$ \begin{aligned} &{\mathrm{min}}_{\omega ,b,{\alpha }_{n},{\widehat{\alpha }}_{n}}{}_{}\dfrac{1}{2}{\Vert \omega \Vert }^{p}+C{\displaystyle\sum\limits_{n=1}^{N}({\alpha }_{n}+{\widehat{\alpha }}_{n})}\\ &s.t{.}\;\;\;\;-\epsilon -{\alpha }_{n}\leqslant \omega \cdot {x}_{n}+b-f\leqslant {\widehat{\alpha }}_{n}+\epsilon \\ &{\alpha }_{n}\geqslant 0,{\widehat{\alpha }}_{n}\geqslant 0\end{aligned}$$ (1) 其中，
${\alpha _n}$ 及${\hat \alpha _n}$ 表示超过损失带的上下方的损失，$f$ 表示真实值；$\omega $ 及$b$ 表示超平面的法向量及截距；常数$C$ 为正则化系数；当$p = 2$ 时，式（1）被称为Tikhonov正则化[7]。在将该规划问题从非线性函数转化为线性可分问题的过程中，利用了内积运算实现将输入映射到高维特征空间的一种简化计算方式，支持向量机通过引入核方法，即定义映射函数内积为核函数，以避免内积的显式计算问题，核函数一般包括有线性（Linear）核函数、多项式（Polynomial）核函数、径向基（Radial Basis）核函数等[4]。
2 大型铁路客运车站客流量变化的特点
以汉口站为例，分析大型铁路客运车站客流量随时间变化的一般特点。汉口站是衔接我国横纵2条主要干线—沪汉蓉大通道及京广线的重要枢纽，现有接发列车衔接方向共计14个，包括京广汉口联络线上下行、合武上下行、汉口汉西联络线上下行、汉宜上下行、汉丹客车线上下行、武孝城际上下行、武孝京广外绕线、武孝京广联络线。汉口站集高速、普客、城际于一体，是武汉局集团公司直属的一等客运站，车站分高架层、地面层、地下层3层，站房面积7.6万m2，10个高站台，20条股道，日均发送旅客9.1万人，最多可容纳8000人同时候车，客服区域平面图如图2所示。
采用汉口车站2017年1月1日—12月31日日发送客流数据作为样本数据集，进行时间变量与客流量的相关分析，研究汉口站的客流变化情况，如图3所示。
由图3可知，汉口车站的客流变化具有如下特点：
（1）年度客流呈现明显的周期性波动，客流总体以7日为一个周期，这主要是由工作日和非工作日客流种类的差异所造成的，工作日多为通勤、商务、公务客流，非工作日则多为旅游、探亲客流；
（2）长周期内因节假日出现大幅客流激增，呈现多个明显的高峰，包括年初春运去返程客流2次出行高峰、清明节出行高峰、劳动节出行高峰、端午节出行高峰、暑运出行高峰（表现出长期性，但峰值不高）、国庆出行高峰（年度出行最高峰）及年尾的元旦出行高峰；这些突发大客流与平时客流特点存在明显差异。
3 支持向量回归模型的预测实例
3.1 汉口车站发送客流量的回归预测
采用2017年1月1日—12月31日汉口站的日实际发送旅客人数数据共计365条，以前70%作为训练数据，后30%作为测试数据，应用支持向量回归模型进行分析。
采用Python 3.6软件建模，IDE为Pycharm社区版，运行环境为：Microsoft Windows 8.1 (64 bit) Professional，Intel(R) Core(TM) i5-3230M CPU @ 2.60 GHz，8GM RAM。
考虑到原始数据呈现的非线性，如图3所示，采用径向基作为支持向量机核函数。图4为汉口站使用SVR模型的预测结果，训练集与测试集由图中的灰线区分，绿色曲线表示汉口车站真实发送客流量，红色曲线为SVR预测结果，蓝色曲线表示预测值与真实值的绝对误差。
由图4可知，因受节假日期间突发性大客流影响，由SVR模型计算得到的汉口车站全年客流量预测值的误差偏大。本文研究主要关注车站客流长期性、周期性变化进行预测，故将这些突发大客流作为噪点剔除。本文选择将节日假期及节日假期开始前的一天，作为剔除点，包括春节（1月13日—30日）、清明节（4月1日—4日）、劳动节（4月28日—5月1日）、端午节（5月27日—5月30日）、国庆节（9月29日—10月8日）、元旦节（12月29日—12月31日），共计43天。消除节假日期间突发大客流的影响后，得到预测结果如图5所示。
3.2 模型预测误差量化分析
使用平均绝对误差（MAE，Mean Absolute Error）、均方根误差（RMSE，Root Mean Square Error）、拟合度（R2，R-squared）3个指标对SVR模型的预测误差进行量化分析析[8]：
$$ E_{\rm{MAE}}=\frac{1}{n}{\sum\limits_{i=1}^{n}\left(\left|{P}_{{\text{预测值}}, i}-{P}_{{\text{原始值}}, i}\right|\cdot 100{\text{%}} \right)}$$ (2) $$ E_{\rm{RMSE}}=\sqrt{\frac{1}{n}{\sum\limits_{i=1}^{n}{\left({P}_{{\text{预测值}}, i}-{P}_{{\text{原始值}}, i}\right)}^{2}}}$$ (3) $$E_{\rm{{R^2}}} = 1 - \frac{{RSS}}{{TSS}}$$ (4) 其中，TSS为原始数据的固有方差，RSS为回归预测值与实际值的残差平方和。
表1为基于SVR模型、剔除节假日前后的汉口站发送客流量预测误差对比，可知：排除节假日突发大客流的影响后，由SVR模型计算得到车站发送客流量预测值的精度可明显提高。
表 1 排除节假日前后的汉口站发送客流量预测误差对比误差指标 包含节假日 剔除节假日 RMSE 8099.46 2721.42 MAE 1918.38 880.31 R2 0.5295 0.8999 4 结束语
准确预测铁路繁忙大型客运站的发送客流量有利于铁路运输部门充分考虑客流状态及其变化情况，评估和优化车站人员及设备布置效果，完善客运规划管理，为旅客出行提供更优质的服务。
以汉口车站2017年全年发送客流量数据作为样本数据集，应用支持向量回归模型，对汉口车站全年客流量进行预测和误差分析，在剔除节假日突发大客流的影响后，对车站日常客流量预测的精度明显提高。
-
表 1 2016—2021年上海站客流量（从大到小排序）
序号 日期 客流量(人次) 1 2019-05-01 189841 2 2021-05-01 187263 3 2019-10-01 184243 4 2018-10-01 179396 ... ... ... 22 2016-10-01 153110 ... ... ... 27 2017-04-29 149480 ... ... ... 212 2020-05-01 105975 ... ... ... 
下载: 导出CSV
-
[1] 林晓言,李明真,陈小君. 疫情对我国铁路行业发展的影响与对策 [J]. 铁道经济研究,2020(2):1-6. DOI: 10.3969/j.issn.1004-9746.2020.02.001 [2] 新华社. 上半年全国铁路发送旅客8.18亿人次[EB/OL].（2020-07-09）[2021-06-22]. http://www.xinhuanet.com/travel/2020-07/09/c_1126214823.htm. [3] 黄召杰,冯 硕. 灰色预测模型在铁路客流预测中的应用 [J]. 交通科技与经济,2014,16(1):57-60. DOI: 10.3969/j.issn.1008-5696.2014.01.016 [4] 曹鸿飞,张 铭,李 平. 灰色动态模型群在城市轨道交通客流预测中的应用研究 [J]. 铁路计算机应用,2012,21(3):1-3,8. DOI: 10.3969/j.issn.1005-8451.2012.03.001 [5] 郭 淼. 基于支持向量回归的大型客运站客流量预测应用研究 [J]. 铁路计算机应用,2021,30(3):15-18. DOI: 10.3969/j.issn.1005-8451.2021.03.004 [6] 孟 歌,王洪业,李丽辉,等. 基于EMD的SVR方法在铁路客流预测中的应用 [J]. 铁路计算机应用,2020,29(4):28-32. DOI: 10.3969/j.issn.1005-8451.2020.04.007 [7] 滕 靖,李金洋. 考虑日期属性和天气因素的铁路城际短期客流预测方法 [J]. 中国铁道科学,2020,41(5):136-144. DOI: 10.3969/j.issn.1001-4632.2020.05.16 [8] CHEN TIANQI, GUESTRIN CARLOS. XGBoost: A Scalable Tree Boosting System[C]// In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD '16). New York, USA: Association for Computing Machinery, 2016: 785–794.
-
期刊类型引用(1)
1. 史方圆，宗智诚，马毅华，傅鹏，吴文波. 基于雷视融合的涉铁工程防侵限监测系统的设计与实现. 铁路计算机应用. 2024(11): 32-37 . 
本站查看
其他类型引用(0)
计量
- 文章访问数: 223
- HTML全文浏览量: 127
- PDF下载量: 59
- 被引次数: 1
