我国铁路具有分布广、里程长、数据分散、类别庞杂、周边环境复杂等特点。铁路基础设施空间数据作为铁路的关键信息资产，能够为开展大规模的线路巡检、检测、维护等工作提供辅助决策^[1]。但是，我国铁路仍存在基础设施空间数据缺失、无法完全掌握线路周边真实环境、空间数据难以集中管理等问题。因此，高效、准确地采集和管理铁路基础设施空间数据，对铁路工作人员全面掌握基础设施资源分布、落实精准化管理、开展日常巡检维修、进行应急抢险救援等工作具有重大意义。

目前，空间数据采集的研究主要集中在基于连续运行参考站系统（CORS，Continuously Operating Reference System）采集、三维激光扫描、无人机遥感测绘、移动测量等技术^[2]。任洁^[3]采用全球定位系统−实时动态（GPS-RTK，Global Positioning System & Real-Time Kinematic）技术在兰州某段既有线路进行不等间距实地测量，验证了所提方法的实用性。陈隆^[4]结合铁路线路的实际环境，提出利用无人机倾斜摄影测量技术进行铁路地理信息空间数据采集，并构建了可视化的三维模型，所采集的数据能够直观地反映地物的详细信息。移动测量技术是当今测绘界的前沿技术，能够在车辆高速行进时实现道路及周边地物的空间位置和属性数据的快速采集^[5]，提高数据的采集效率，因而是本文主要的研究内容。在铁路基础设施空间数据管理方面，晋杰等人^[6]搭建了基于地理信息系统（GIS，Geographic Information System）的数据环铁平台，该平台对中国铁道科学研究院集团有限 公司国家铁道试验中心（简称：国家铁道试验中心）的环行铁路试验线所采集的三维空间数据进行管理，实现了环形铁路基础设施的信息集成和可视化表达。

为进一步提高铁路基础设施空间数据的采集效率及管理水平，本文研究了铁路基础设施空间数据采集及管理技术，设计了基于移动实景测量技术的便携式非接触采集装置（简称：采集装置），以及铁路基础设施三维空间数据管理系统（简称：管理系统），实现在复杂场景下，对铁路基础设施空间数据的快速、精确采集及有效管理。

1   铁路基础设施空间数据现状分析

铁路地理信息平台是以实现铁路地理信息和服务共享为目标的信息化基础平台，是铁路地理信息数据统一管理中心、统一功能服务中心和统一发布中心。在中国国家铁路集团有限公司发布的《铁路信息化总体规划》中，进一步明确铁路地理信息平台是一体化集成平台中铁路数据服务平台的重要组成部分。铁路地理信息平台中包含国家基础地理信息数据、铁路专业公用地理信息数据和铁路专业专用地理信息数据，采用“一张图+N应用”的服务模式，提供面向全国铁路的铁路地理信息数据和服务。该平台包括132种铁路数据，主要有全国铁路干线、合资铁路、客运站、货运站、专题地图、中欧班列（铁路线）等数据，涵盖铁路路基、桥梁、隧道、信号机、基站等基础设施。

铁路地理信息平台使用的是国家地理信息公共服务平台“天地图”（简称：“天地图”）的数据，地图比例尺为1∶2 000。表1为“天地图”数据服务内容。

表  1  “天地图”数据服务内容

数据类型	具体内容
矢量瓦片地图	水体、地貌、土质、植被等自然地理要素，以及居民地、 交通网、行政区域界线等社会经济因素
影像瓦片地图	地面分辨率达到2.5 m
地形瓦片地图	用等高线表示地面起伏的地图
中文注记	省、市、县（区）、乡等区域名称
地名、地址、兴趣点	民用机场、高等院校、客运火车站、5A级景区①、公园、 医院、政府机构、事业单位、餐饮、宾馆、地名、地址、 地铁站、公共设施等
注：①5A级景区：国家AAAAA级旅游景区。

下载: 导出CSV 

| 显示表格

铁路专业公用地理信息数据指铁路车务、机务、工务、电务、车辆、供电等业务部门之间共享的铁路专业空间数据。铁路专业专用地理信息数据主要包括铁路各专业内部专用的空间数据，以及与本专业的业务密切相关、与其他专业关系不大、不需要在专业之间进行共享的铁路专业空间数据。

目前，铁路地理信息平台已基本完成全国铁路线路空间数据的建设，而对于工务、电务、供电、给水等各专业设备设施空间数据的建设范围较小，现已完成部分线路的桥梁、信号机、基站和车站等空间数据的建设。此外，对于近几年国家新建铁路线的空间数据缺失较多，因此还需对全国各铁路线、各专业的设备设施及新建铁路线进行大量的空间数据采集工作，并对采集的数据进行集中管理和维护。

2   采集装置

2.1   装置功能

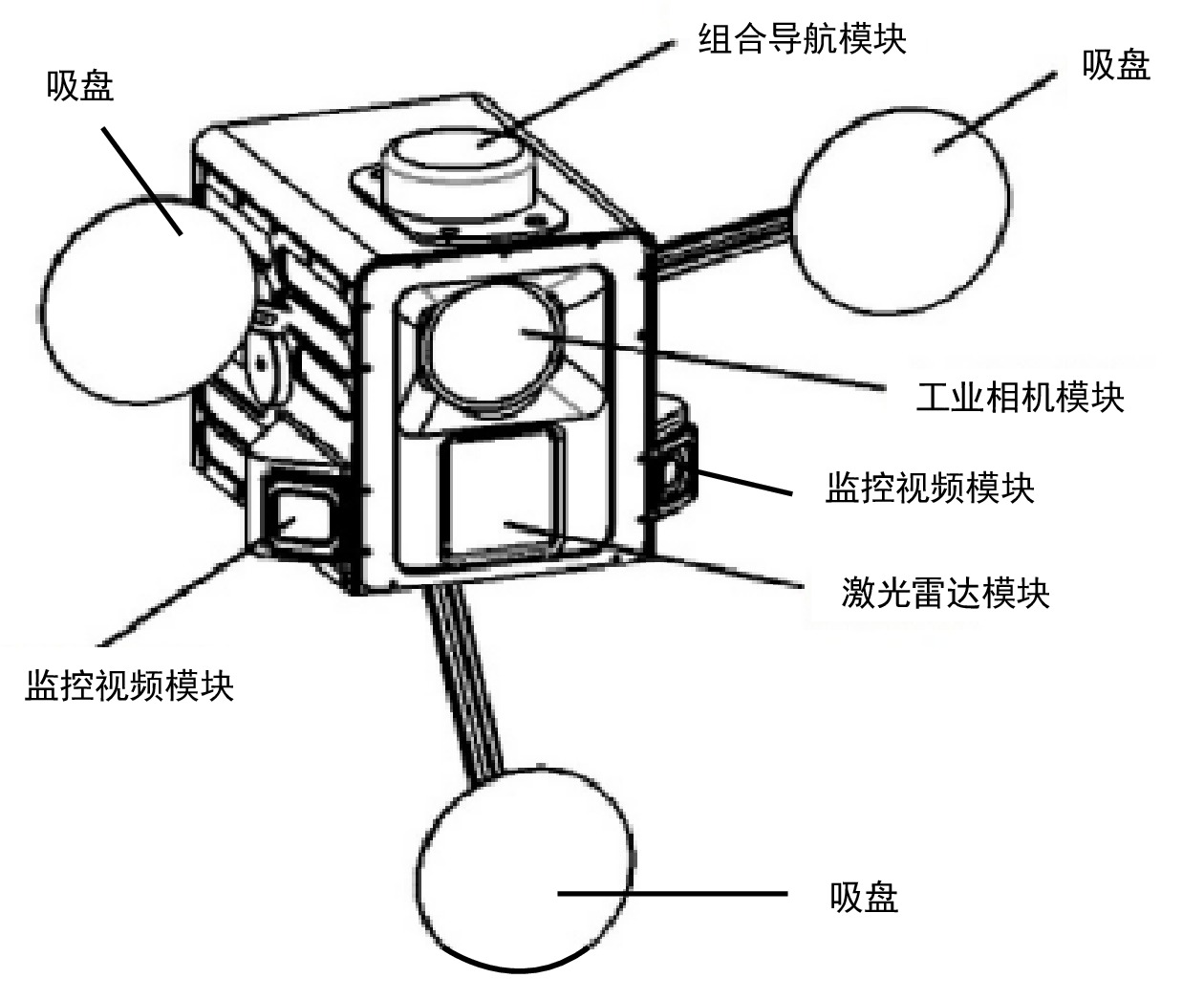
为了满足铁路基础设施空间数据采集的实际需求，本文研制了基于移动实景测量技术的便捷式非接触采集装置，实现了铁路基础设施空间数据的快速、精准采集。采集装置采集的内容主要有3类，分别为坐标数据（包含铁路基础设施高精度三维坐标、列车行驶轨迹）、点云数据（包含轨旁基础设施、接触网、周边地形等点云数据）、影像与视频（包含装置前视70°范围内可量测实景影像数据、运行期间视频等）。采集装置由激光雷达模块、工业相机模块、组合导航模块、监控视频模块、网络通信模块、环境适应模块和综合处理模块组成。

（1）激光雷达模块：获取目标的距离、方位、高度、速度、姿态、形状等数据，从而对目标进行探测、跟踪和识别。

（2）工业相机模块：采用分辨率为 890万像素、1英寸（1英寸≈2.54 cm）CMOS芯片的工业相机。该相机具有噪点低、分辨率高、图像质量好等特点。工业相机模块通过千兆以太网接口实时传输非压缩图像，在全分辨率下的最高帧率可达到13 f/s。

（3）组合导航模块：由全球导航卫星系统（GNSS，Global Navigation Satellite System）和惯性测量单元（IMU，Inertial Measurement Unit）组成，姿态测量精度为0.02°。GNSS包括北斗卫星导航系统、全球定位系统（GPS，Global Positioning System）、格洛纳斯卫星导航系统（GLONASS，Global Navigation Satellite System）。IMU采用高精度工业级惯性器件，输出频率为200 Hz。

（4）监控视频模块：由2台摄像机组成，其中，单台摄像机的视场角为100°。2台摄像机进行组合，它们的视场角重叠20°，组成视场角为180°的前向摄像机。监控视频模块所采集的影像数据通过4G/5G通信链路实时传输到管理系统。

（5）网络通信模块：内置4G/5G通信模块，通过收取RTK差分改正数据，将组合导航模块的定位精度提高到厘米级；同时，将传送采集装置状态、监控视频等数据传输到管理系统。

（6）环境适应模块：用于确保工业相机的感光器件互补金属氧化物半导体（CMOS，Complementary Metal Oxide Semiconductor）在野外低温环境的运行安全。当监测到运行温度过低时，该模块自动启动预热系统，将敏感器件加热到0°以上，以保证采集装置正常发挥。

（7）综合处理模块：采用内置的高性能嵌入式计算机，将激光雷达和组合导航数据进行融合解算，得到点云数据；将点云数据和影像融合，形成可量测影像数据，并存储到内置存储器；将监控视频模块获得的视频数据回传到管理系统。

采集装置模型如图1所示，通过吸盘固定在列车驾驶室挡风玻璃内侧。

图  1  采集装置模型

下载: 全尺寸图片 幻灯片

2.2   试验测试

2.2.1   试验环境

本文选取国家铁道试验中心的环形铁路试验线进行试验。环形铁路试验线包括大环线、小环线及新建的城轨试验线，可进行机车车辆、铁道建筑、通信信号、铁道电气化设施、客货运输、特种运送等多专业的科学试验。在本次试验中，列车以160 km/h的速度绕环形铁路试验线大环线（周长为9 km）运行一圈，实现铁路基础设施三维空间数据的采集。为满足不影响列车正常运行和调度要求，试验采取添乘模式进行数据采集。便携采集装置固定于驾驶室挡风玻璃内侧，通过添乘模式完成数据采集作业。

2.2.2   试验结果

采集试验线路数据，获取了试验线路基础设施（包括桥梁、涵洞、隧道、轨道、防护栅栏、接触网、信号机等）的三维坐标数据、点云数据和实景影像数据，并对其精度进行分析与验证。图2为含有接触网、轨道、防护栅栏等基础设施的点云数据和实景影像数据。采集装置技术指标试验结果如表2所示。可以发现，采集装置能够实现铁路沿线的三维坐标数据、可量测实景影像数据、点云数据、周边环境视频数据的快速、精准、安全及一体化采集。

图  2  试验采集数据

下载: 全尺寸图片 幻灯片

表  2  采集装置技术指标的测试结果

技术指标	测试结果
点云精度	平面坐标精度高于15 cm，高程坐标精度高于10 cm
量测精度	满足地图比例为1∶2 000的测量精度
定位精度	平面坐标精度高于20 cm；姿态精度（横滚/俯仰） 0.02°
照片分辨率/像素	4 096×2 160
视频分辨率/像素	1 920×1 080
实景测量视场角	水平视场角与垂直视场角均为70°

下载: 导出CSV 

| 显示表格

在对铁路基础设施三维空间数据精度进行验证之后，本文对试验数据进行清洗、整理及入库处理，并构建了精确的线路里程与空间位置关系。同时，在铁路基础设施三维空间数据管理系统中，实现了对铁路基础设施三维空间数据的集中存储与管理维护，提供线路可视化、统计分析、数据管理和系统管理等功能。

3   关键技术

3.1   轻量化存储与快速查询

本文采用了面向铁路基础设施三维空间数据的轻量化存储与快速查询技术，其中，三维空间数据包括栅格数据和矢量数据。轻量化存储与快速查询技术采用瓦片金字塔对栅格数据进行压缩，将其分割为1组瓦片，并存储于数据库服务器，建立合适的数据索引结构来存储瓦片，实现了轻量化存储与快速查询。轻量化存储与快速查询技术采用串表压缩（LZW，Lempel-Ziv-Welch ）算法^[7]，对矢量数据的几何信息和属性信息进行压缩。LZW算法具有简单、快速、易于硬件实现、压缩效果较好等优点，且可通过一次性读取全部数据实现数据的存储。压缩后的数据依据MBTiles规范进行存储，通过应用服务器处理后发布生成瓦片地图，实现数据的快速查询。

3.2   线性参考系统构建

线性参考系统（LRS，Linear Reference System）是国际上先进的线性空间数据组织和构建模型。LRS能够对未知要素的位置信息通过其与己知线性要素起点位置之间的相对位置关系进行表示或测量，而不是以经纬度或平面坐标系的方式表示，实现了线性设施中任意两点之间里程的精确量算^[8]。同时，LRS能够实现对任意空间位置和方向进行任意里程位置的精确定位和查询。

管理系统采用ArcGIS的线性参考工具（LRT，Linear Referencing Tools），对路径要素类和事件表这两种数据结构进行处理。基于高精度高密度的行驶轨迹，依据给定路段起止点信息，本文构建了铁路LRS，将铁路线路和基础设施的经纬度位置信息通过线性要素的相对位置来表示，建立铁路基础设施空间数据与台账数据之间的高度关联，为铁路基础设施空间位置的快速查询提供依据。

4   管理系统

4.1   系统架构

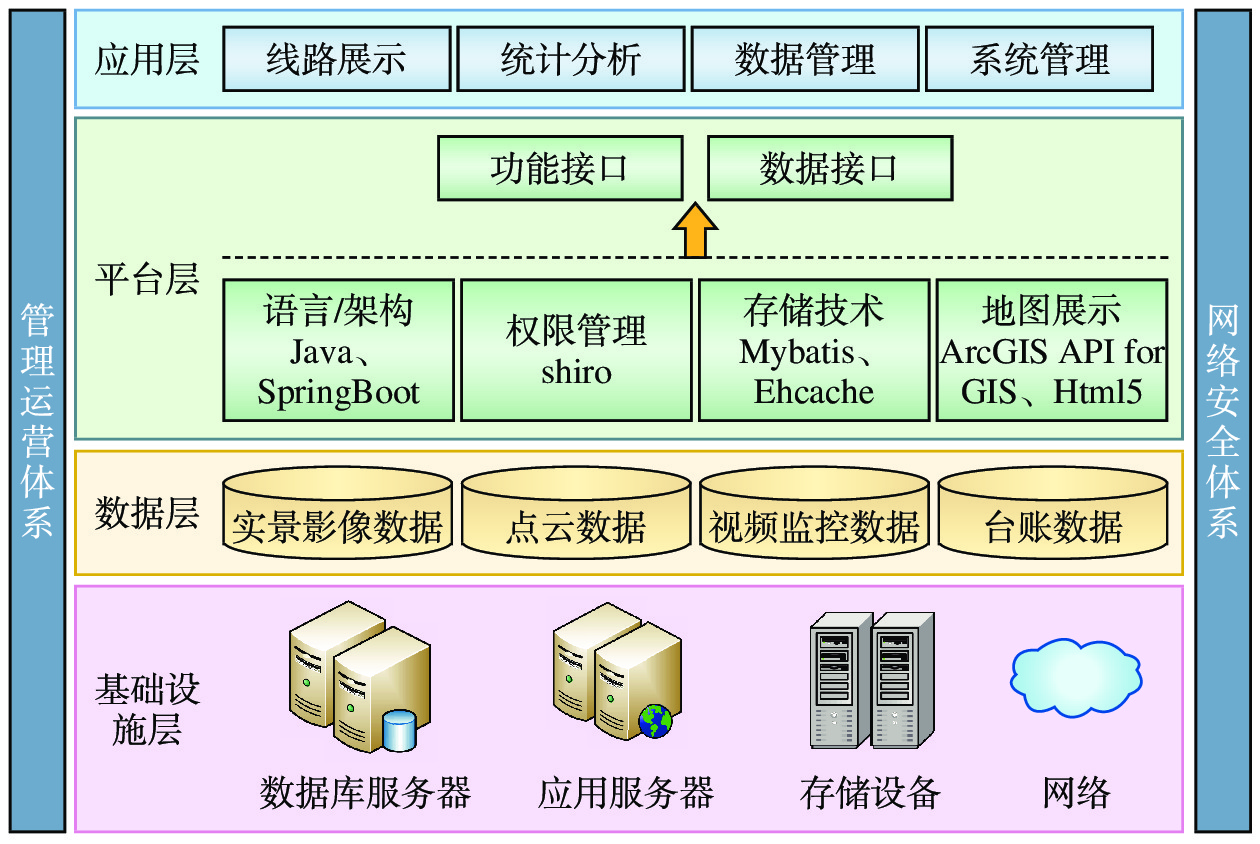
本文基于上述两种关键技术，研发了铁路基础设施空间数据管理系统（简称：管理系统），实现将采集装置所获取的多种铁路基础设施三维空间数据进行集中管理与存储。管理系统采用多层架构，从下到上依次为基础层、数据层、平台层和应用层，如图3所示。

图  3  管理系统总体架构

下载: 全尺寸图片 幻灯片

（1）基础层：主要包括服务器、存储、网络设备等硬件设施，是管理系统的运行环境。

（2）数据层：在对数据进行有效、准确采集的基础上，基于轻量化存储和快速查询技术，构建铁路地理信息空间数据库，实现对点云数据、实景影像数据、视频监控数据、台账数据等铁路基础设施数据的统一管理。

（3）平台层：包括管理系统所采用的基础技术框架、组件，以及为应用层提供的数据和GIS功能服务接口。

（4）应用层：包括各个业务功能模块，主要实现对铁路基础设施的可视化定位和查询、基于实景测量的空间分析与量测、铁路线路周边状况监控等功能。

4.2   系统功能

管理系统包括铁路线路可视化、统计分析、数据管理和系统管理4大功能，实现了对铁路基础设施空间数据的统一集中管理。

（1）铁路线路可视化

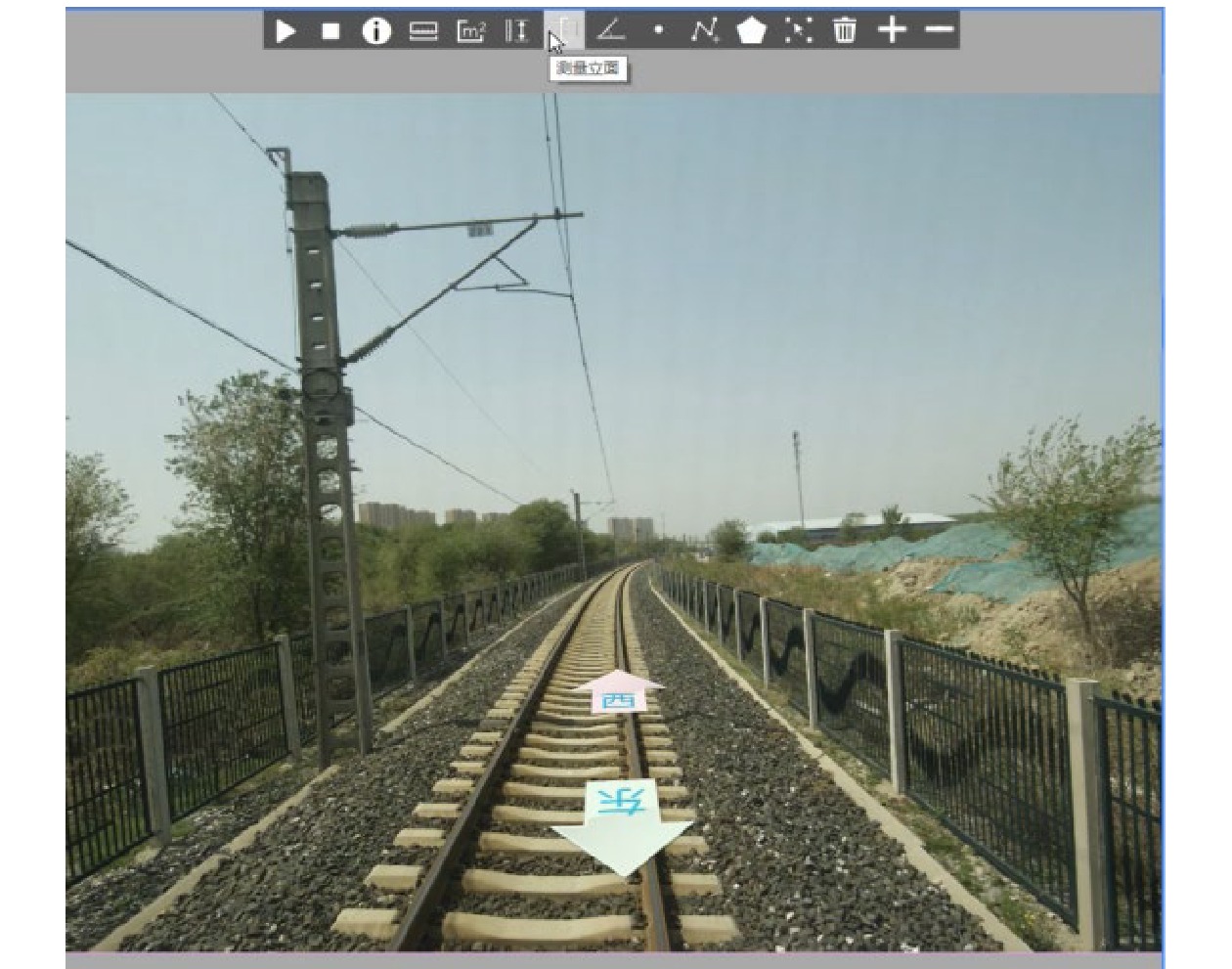
铁路线路可视化功能具有铁路线路及其基础设施的二维地图、三维实景地图、多时相地图的可视化展示功能，以及统一的检索入口，能够实现铁路基础设施定位查询、铁路线路里程的定位功能。铁路可视化功能支持以点选、框选方式进行设备设施定位查询，还可以提供对三维实景对象的量算分析功能，例如，量测对象的距离、面积、垂距、立面、角度等。同时，铁路线路可视化功能还可以关联铁路基础设施台账数据，实现基础设施基本信息的查看。基于多时相地图，铁路线路可视化功能可调阅和对比不同时间段铁路实景影像数据，以及不同时段铁路线路周边状况监控视频回放。典型示范铁路线路的三维实景影像如图4所示。

图  4  典型示范铁路线路的三维实景影像

下载: 全尺寸图片 幻灯片

（2）统计分析

统计分析功能能够实现对空间数据的分类与综合评价，涉及空间和非空间数据的处理和统计计算。为了将地图上某类对象的某些属性进行横向或纵向比较，统计分析功能将这些属性制成统计专题地图，以进行直观的综合评价。

统计功能还可以按目录树和地图框两种选择方式查询或统计指定范围内基础设施的数量和类型，并将统计结果在地图上进行可视化展示。

（3）数据管理

数据管理功能以铁路工务、电务、供电等专业为标准，对线路台账数据、实景测量数据、点云数据、视频数据等进行分类管理。同时，数据管理功能还能依据不同权限提供数据资源的上传、下载、查询、查看等，实现数据资源的共享利用。

（4）系统管理

系统管理功能支持系统用户管理、功能菜单权限管理、系统服务状态监控等，可实现数据库运行监控、系统访问日志留痕等。

5   结束语

本文分析了我国铁路基础设施空间数据建设现状，研制了便携式非接触空间数据采集装置，并搭建了铁路基础设施空间数据管理系统，实现了铁路基础设施空间数据的实时采集和集中管理。本文成果有效地提高了铁路线路相关数据的采集效率与信息化管理水平，为数字孪生铁路、智慧铁路的建设提供了科学、可靠、实用的数据支撑和管理平台。