一种优化的Canny边缘检测算法

田贝乐; 牛宏侠; 刘义健

doi:10.3969/j.issn.1005-8451.2021.10.04

一种优化的Canny边缘检测算法

田贝乐^{1, 2},
牛宏侠^{1, 2,},
刘义健^{1, 2}

1.
兰州交通大学　光电技术与智能控制教育部重点实验室，兰州　 730070
2.
甘肃省高原交通信息工程及控制重点实验室，兰州　730070

基金项目: 国家自然科学基金（61863024）、甘肃省科技引导计划（2020-61-14）

详细信息

作者简介:
田贝乐，在读硕士研究生

牛宏侠，副教授

中图分类号: TP391
计量
- 文章访问数: 395
- HTML全文浏览量: 235
- PDF下载量: 46
出版历程
- 收稿日期: 2021-02-06
- 刊出日期: 2021-10-30

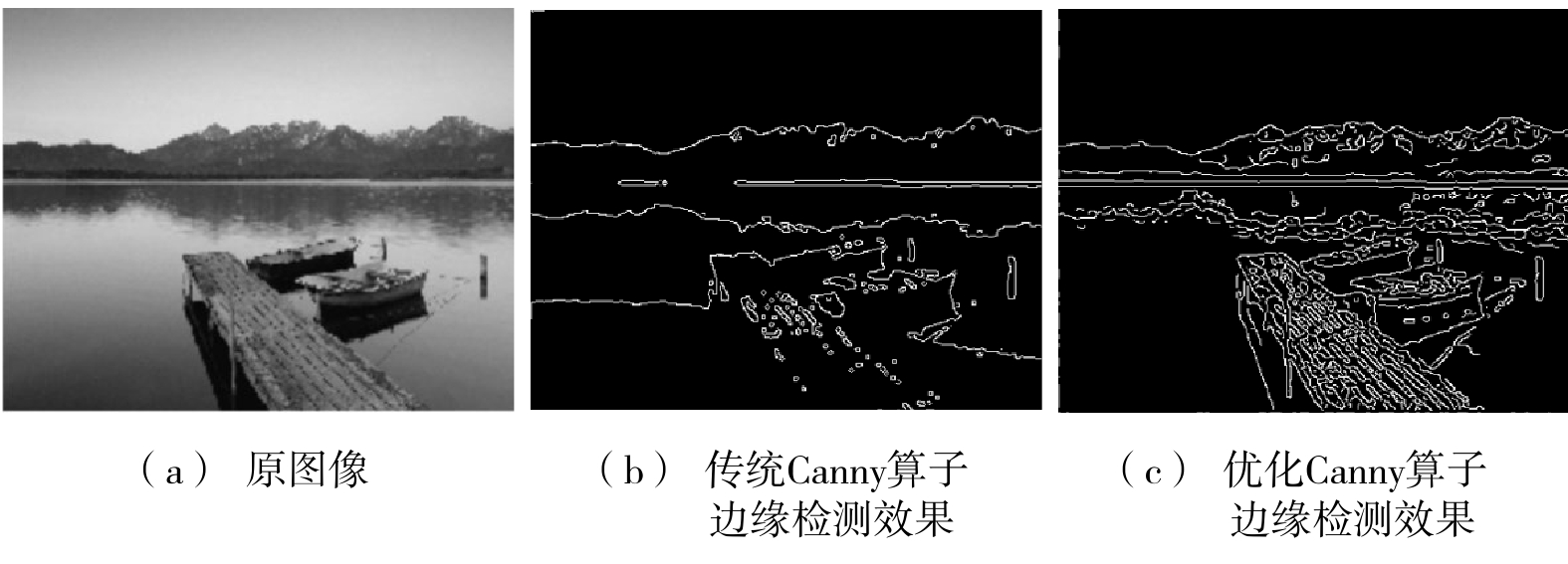
Optimized Canny edge detection algorithm

TIAN Beile^{1, 2},
NIU Hongxia^{1, 2,},
LIU Yijian^{1, 2}

1.
Key Laboratory of Optoelectronic Technology and Intelligent Control of Ministry of Education, Lanzhou Jiaotong University, Lanzhou　 730070, China
2.
Gansu Provincial Key Laboratory of Traffic Information Engineering and Control, Lanzhou 　730070, China

摘要

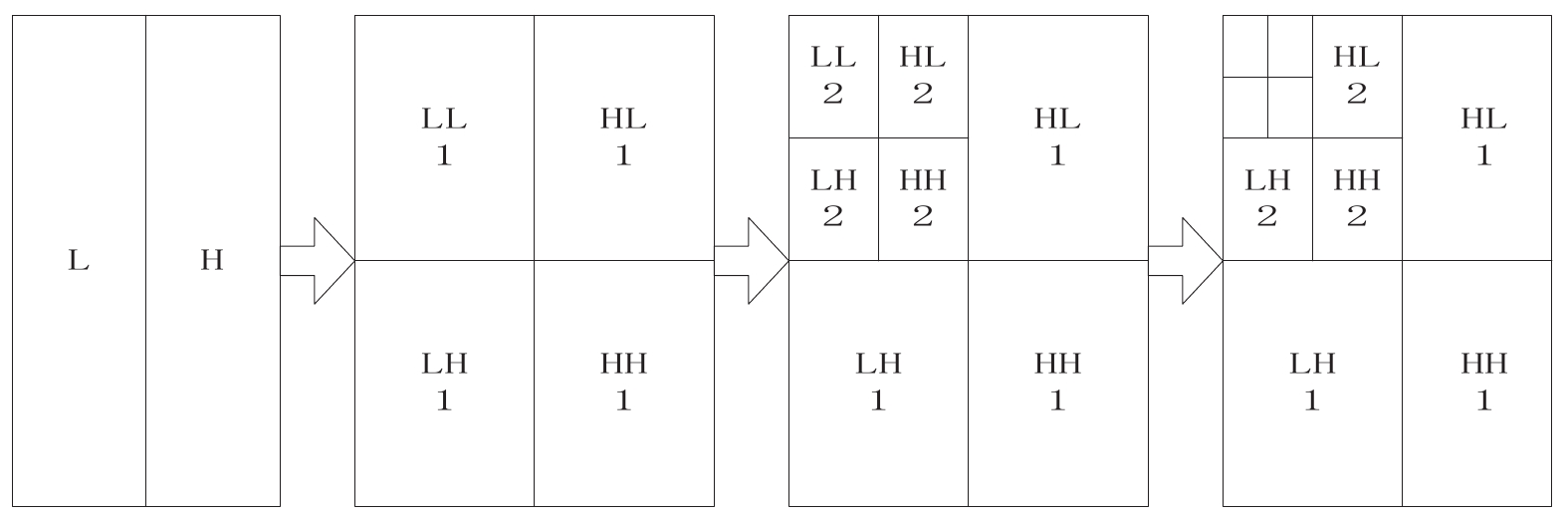
摘要: 在对Canny边缘检测理论研究基础上，针对Canny边缘检测算法在高斯滤波、梯度计算和高低阈值的确定上的缺陷，提出一种改进的小波变换法，替代高斯滤波，实现对图像的降噪，同时，优化了原有梯度幅值和方向的计算方法，采用改进的迭代算法对高低阈值进行计算。运用MATLAB仿真实验对比优化后的Canny边缘检测算法与传统Canny边缘检测算法。结果表明，优化后的Canny边缘检测算法可使检测结果拥有更多的边缘细节，提高了检测的精度和准确度。
- Canny /
- 边缘检测算法 /
- 高斯滤波 /
- 小波变换 /
- 迭代法
Abstract: Based on the research of Canny operator edge detection theory, aiming at the shortcomings of the Canny edge detection algorithm in Gaussian filtering, gradient calculation and determination of high and low thresholds, this paper proposed an improved wavelet transform, replaced Gaussian filtering to reduce the noise of the picture, and optimized the original gradient amplitude and direction, an improved iterative algorithm was used to calculate the high and low thresholds. MATLAB simulation experiment was used to compare the edge detection algorithm of optimized Canny and traditional Canny. The results showed that the optimized Canny edge detection algorithm can make the detection results have more edge details and improve the detection precision and accuracy.
- Canny /
- edge detection algorithm /
- Gaussian filtering /
- wavelet transform /
- iterative algorithm

HTML全文

图 1 图像的三级小波分解

下载: 全尺寸图片幻灯片

图 2 滤波效果对比

下载: 全尺寸图片幻灯片

图 3 风景图像效果对比

下载: 全尺寸图片幻灯片

图 4 地面图像效果对比

下载: 全尺寸图片幻灯片

图 5 红细胞图像效果对比

下载: 全尺寸图片幻灯片

参考文献(12)

[1]	李彦, 赵其峰, 闫河, 等. Canny算子在PCBA目标边缘提取中的优化应用 [J]. 光学精密工程,2020,28(9):2096-2102. DOI: 10.37188/OPE.20202809.2096
[2]	李长有, 陈国玺, 丁云晋. 改进Canny算子的边缘检测算法 [J]. 小型微型计算机系统,2020,41(8):1758-1762. DOI: 10.3969/j.issn.1000-1220.2020.08.031
[3]	王植, 贺赛先. 一种基于Canny理论的自适应边缘检测方法 [J]. 中国图像图形学报,2004,9(8):957-961.
[4]	Mario Hernández-Hernández, José Luis Hernández-Hernández, Edilia Rodríguez Maldonado, et al. Modern code applied in stencil in edge detection of an image for architecture Intel Xeon Phi KNL [M]. Springer International Publishing, 2019.
[5]	郑鹏,王雨,苑泽伟. 基于Canny算子的IC卡字符边缘检测及分割的研究 [J]. 计算技术与自动化,2018,37(3):118-121.
[6]	BISWAS R, ROY S, PURKAYASTHA D. An efficient content-based medical image indexing and retrieval using local texture feature descriptors [J]. International Journal of Multimedia Information Retrieval, 2019, 8(4): 217-231. DOI: 10.1007/s13735-019-00176-9
[7]	余松煜, 周源华, 张　瑞, 等. 数字图像处理[M]. 上海: 上海交通大学出版社, 2007.
[8]	李牧,闫继红,李戈,等. 自适应Canny算子边缘检测技术 [J]. 哈尔滨工程大学学报,2007(9):1002-1007. DOI: 10.3969/j.issn.1006-7043.2007.09.010
[9]	董昱,高云波,刘翔. 改进的遗传算法在Canny算子阈值选取中的应用 [J]. 兰州交通大学学报,2014,33(6):1-5. DOI: 10.3969/j.issn.1001-4373.2014.06.001
[10]	朱威,韩巨峰,陈朋,等. 基于噪声点多级检测的自适应中值滤波算法 [J]. 光电工程,2013,40(10):63-69.
[11]	秦亚辉,冯景辉,陈立定. 基于小波变换的信号去噪方法研究 [J]. 信息技术,2010,34(1):53-57. DOI: 10.3969/j.issn.1009-2552.2010.01.016
[12]	李志鹏,于鸿彬,邵宏宇. 基于改进Canny边缘检测算法的道路标线检测实验研究 [J]. 实验技术与管理,2019,36(9):137-141, 148.

施引文献(10)

期刊类型引用(7)

1.	杨涛存，史维峰，李国华，代明睿，李文浩，杜文然. 人工智能视觉大模型在铁路线路异物入侵场景中的应用. 中国铁路. 2025(01): 23-29+48 . 百度学术
2.	王增卿，谢征宇，姜忆玲，王佳丽，管岭，王力. 面向铁路周界远小目标入侵检测的视频超分辨率重建技术研究. 中国铁道科学. 2025(01): 200-211 . 百度学术
3.	杨文，胡昊，李凌志，冯爽，吴浩楠. 基于机器视觉的铁路限界入侵检测方法. 铁道科学与工程学报. 2025(03): 1328-1343 . 百度学术
4.	赵仲瑜，唐伟忠，张文辉，蒲伟，牛超群. 基于YOLOv5的铁路接触网异物检测模型初步研究. 铁路计算机应用. 2024(02): 13-18 . 本站查看
5.	郑相波，姚国栋，史方圆，廖炜炼，马清志. 大型施工机械监管系统智能视频分析模型研究. 铁路计算机应用. 2024(04): 23-29 . 本站查看
6.	陈伟迅，柯旭能，孟思明. 基于改进YOLOv8的铁路异物侵限检测方法. 机电工程技术. 2024(11): 211-214 . 百度学术
7.	张慧飞，姜汇川，刘宁，李洪. 基于YOLOv5s模型的地铁列车车顶关键部件检测算法研究. 铁路计算机应用. 2024(12): 1-7 . 本站查看