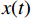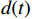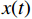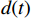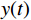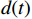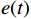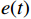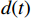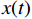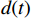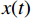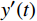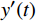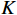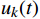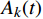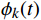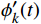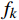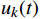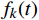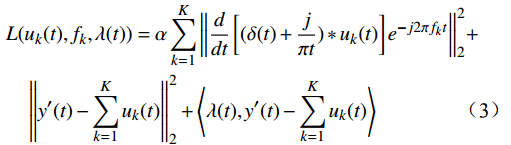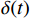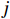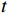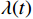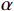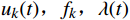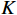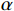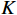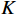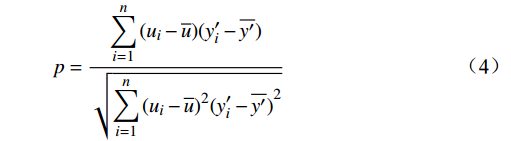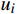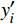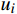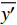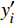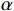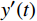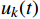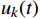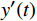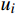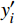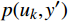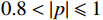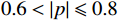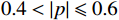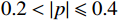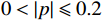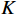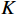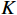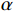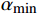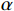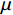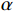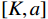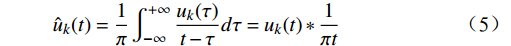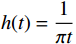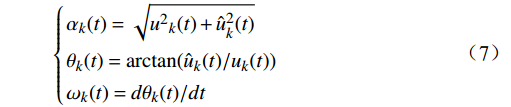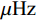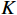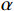Cab signal demodulation method based on VMD and Hilbert transform
-
摘要:
为了提高机车信号的解调精度,提出一种基于参数优化变分模态分解(VMD,Variational Mode Decomposition)和希尔伯特变换的机车信号解调方法。通过最小均方(LMS,Least Mean Square)自适应滤波器对机车天线采集的信号进行滤波;以Pearson相关系数为评价指标优化VMD参数,利用VMD对滤波后的信号作模态分解;将每个固有模态(IMF,Intrinsic Mode Function)作希尔伯特变换,构建复数解析式,计算得出机车信号的载频和低频调制信号频率;通过计算机仿真验证该方法在谐波环境下的可行性及解调精度;最后,基于Cortex-M4内核单片机搭建程序运行硬件平台,基于直接数字合成(DDS,Direct Digital Synthesis)器AD9854搭建机车信号发生电路,在渐变频移键控(Ramped FSK,Ramped Frequency-Shift Keying)模式下,产生正交FSK信号,模拟现场机车信号测试环境。通过硬件测试,在低信噪比条件下,载频和调制低频解调的最大误差分别不超过0.1 Hz和0.05 Hz。试验结果表明,该方法具有较强的抗谐波干扰的能力,能够准确解调机车信号。
Abstract:In order to improve the demodulation accuracy of cab signals, this paper proposed a cab signal demodulation method based on parameter optimized Variational Mode Decomposition (VMD) and Hilbert transform. The paper used the Least Mean Square (LMS) adaptive filter to filter the signals collected by the locomotive antenna, used correlation coefficient as the evaluation index, optimized VMD parameters, and used VMD to perform modal decomposition on the filtered signal, applied Hilbert transform to each Intrinsic Mode Function (IMF), constructed complex analytical expressions, and calculated the carrier frequency and low-frequency modulation signal frequency of cab signals, verified the feasibility and demodulation accuracy of this method in harmonic environments through computer simulation. Finally, the paper built a hardware platform for program execution based on the Cortex-M4 core microcontroller, build a cab signal generation circuit based on the Direct Digital Synthesis (DDS) device AD9854. This circuit generated orthogonal FSK signals in Ramped Frequency Shift Keying (FSK) mode to simulate the on-site cab signal testing environment. Through hardware testing, under low signal-to-noise ratio conditions, the maximum error of carrier frequency does not exceed 0.1 Hz, and the maximum error of modulation low-frequency demodulation does not exceed 0.05 Hz. The experimental results show that this method has strong resistance to harmonic interference and can accurately demodulate cab signals.
-
机车信号系统作为重要的车−地通信系统被应用于我国铁路CTCS-0到CTCS-3级别的列控系统,由于铁路线网的复杂度和列车运行速度的提高,列车司机难以清楚观察地面信号机,车载机车信号由原先的辅助作用逐渐转为主体信号[1],车载信号设备接收并解调经由轨道电路传输的机车信号,得到行车信息,指导列车运行。机车信号实际是一种频移键控(FSK,Frequency-Shift Keying)信号,但容易受到牵引谐波干扰而导致车载系统出现掉码、延迟上码、升级显示现象,成为行车的安全隐患[2]。目前,分析FSK信号常见的方法有多种,孔德龙[3]提出自适应滤波法,利用频谱分析机车信号的载频和频偏,再通过自适应滤波器得到上下边频,取包络并二值化后得出低频调制信号。该方法在高斯白噪声下可准确适应不同载频和低频调制信号,但在有频谱泄露的情况下,其解调精度还有待研究。马罗文等人[4]提出快速傅里叶变换(FFT,Fast Fourier Transform)法,对被测信号作FFT可直接得到信号的频率信息,也是常用的频率估计方法,但FFT的非整周期采样问题会影响频谱分析的精度[5]。朱崇巧[6]、佘嘉演等人[7]提出经验模态分解(EMD,Empirical Mode Decomposition)法,使用EMD法对机车信号进行分解,可得到一组固有模态函数(IMF,Intrinsic Mode Function),再对各IMF单独分解,即可得到FSK信号包含的信息。该方法可有效地处理非线性、非平稳信号,但对被分解信号有两点要求:极值点个数和过零点个数相等或相差不大于1;上/下包络线要对称。在实际应用场景中,机车信号不一定能同时满足以上两个条件,所以机车信号的解析可行性及精度容易受影响。
本文提出一种基于参数优化的变分模态分解(VMD,Variational Mode Decomposition)和希尔伯特变换的机车信号解调方法。通过自适应滤波器对从钢轨上采集到的机车信号进行滤波,去除牵引谐波干扰。对滤波后信号进行VMD,以各个IMF与原信号的相关系数为评价依据,自动优化每次VMD参数。对IMF做希尔伯特变换,分析时−频谱图,可准确解析出机车信号载频和低频调制信号。
1 机车信号方法解调
我国铁路采用50 Hz交流电作为牵引电,由接触网、电力机车、钢轨构成牵引电流回路,电力机车的变流电路及非线性负载产生的谐波引起钢轨上机车信号波形畸变[8]。理想情况下,谐波在两条钢轨上均匀传输,牵引电流造成的干扰可相互抵消,实际会因为钢轨漏泄电阻不同、内外侧钢轨长度不同等因素形成差模电流,即不平衡牵引电流,导致干扰不能抵消。表1列出我国铁路标准《铁道信号电气设备电磁兼容性试验及其限值》(TB/T
3073 -2003)给出的部分谐波实验数据。表 1 牵引电流谐波比例谐波
次数谐波
频率/Hz占百
分比谐波
次数谐波
频率/Hz占百
分比谐波
次数谐波
频率/Hz占百
分比1 50 97.3% 8 400 0.36% 15 750 0.74% 2 100 0.45% 9 450 2.76% 16 800 0.32% 3 150 19.88% 10 500 0.34% 17 850 0.70% 4 200 0.53% 11 550 1.64% 18 900 0.27% 5 250 9.74% 12 600 0.34% 19 950 0.72% 6 300 0.41% 13 650 0.99% 20 1000 0.24% 7 350 5.11% 14 700 0.32% 21 1050 0.63% 除了牵引电流谐波造成的干扰,相邻轨道电路之间的干扰和上下行线路之间的干扰也会影响机车信号,后两种干扰可以采用不同中心频率、改造轨道电路结构来避免,不是本文解调方法研究的重点。
1.1 LMS自适应滤波器
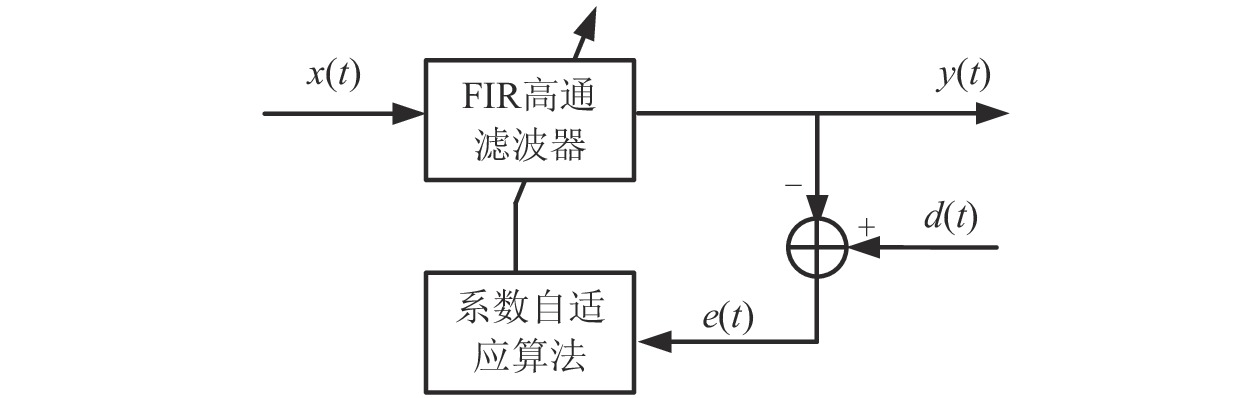
与经典有限冲击响应(FIR,Finite Impulse Response)数字滤波器、无线脉冲响应(IIR,Infinite Impulse Response)数字滤波器固定参数不同,自适应滤波器能够实时根据输入信号的变化调整滤波参数,对非稳定随机变化信号具有较好的滤波效果, LMS自适应滤波器结构图如图1所示[9]。
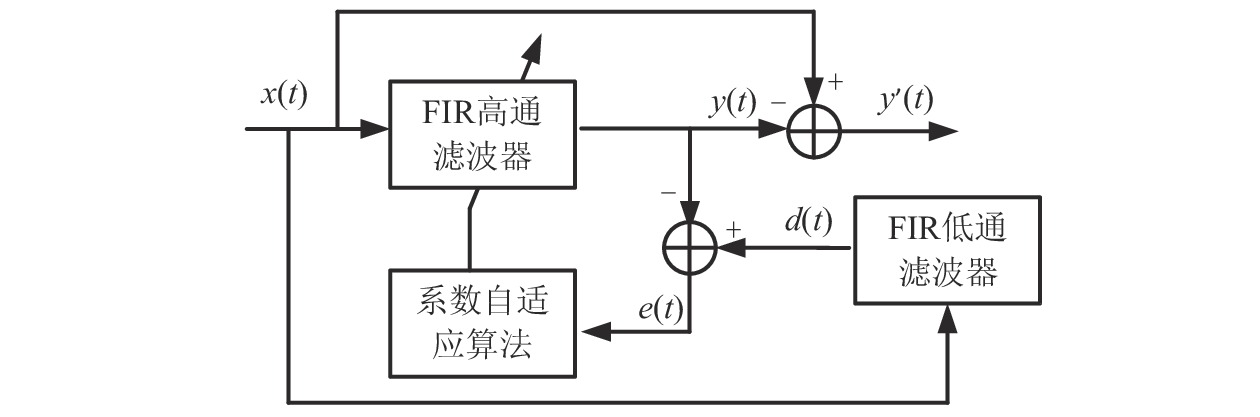
该滤波器包含两部分,主体是一个FIR滤波器,针对ZPW-2000轨道电路信号的调制方式,机车信号的中心载频远高于主要谐波频率,所以该滤波器是一个高通滤波器。另一部分是系数自适应算法,它利用滤波器前一时刻的滤波参数,调节下一时刻的滤波器系数,以适应不同谐波和机车信号,达到反馈控制的效果。滤波器有两个输入信号,分别是
$ x(t) $ 和$ d(t) $ ,$ x(t) $ 是机车天线采集到的带干扰的原始信号,$ d(t) $ 为期望信号,即无干扰的机车信号。系数自适应算法基于滤波器的输出$ y(t) $ 和期望信号$ d(t) $ 的差$ e(t) $ ,系数自适应算法的调节极限是调节$ e(t) $ 接近于0。机车信号是随着不同区段中心频率、不同低频调制信号变化的,所以无法提前用一个统一的函数描述
$ d(t) $ 。考虑到输入信号$ x(t) $ 是机车信号叠加各次谐波的集合,如果将谐波作为期望信号$ d(t) $ ,LMS自适应滤波器即可输出滤掉机车信号后的谐波信号$ y(t) $ ,再将其与$ x(t) $ 相减即可得到滤掉谐波的机车信号$ y'(t) $ ,而谐波信号能够通过增加一个低通滤波器获得,改进后的LMS自适应滤波器结构如图2所示。1.2 参数优化VMD
VMD是一种非递归的模态分解方法,其目的是将滤波后得到的机车信号
$ y'(t) $ 分解成$ K $ 个窄带IMF,y'(t)的计算公式为$$ y'(t) = \sum\limits_{k = 1}^K {{u_k}(t)} $$ (1) 式(1)中,
$ {u_k}(t) $ 为分解出来的IMF。通过分析IMF的特征,即可得到机车信号,每个IMF的波形包含各自的幅度、频率和相位,Uk (t)的计算公式为
$$ {u_k}(t) = {A_k}(t)\cos ({\phi _k}(t)) $$ (2) 式(2)中,
$ {A_k}(t) $ 为该IMF的包络,包络大于0,且缓慢变化;$ {\phi _k}(t) $ 为相位,对其求一次导数$ \phi {'_k}(t) $ 即可得到该IMF所包含的瞬时频率$ {f_k} $ 该频率也称为该IMF的中心频率。求解
$ {u_k}(t) $ 和$ {f_k}(t) $ 可以转化成一种最小化约束变分问题,将目标函数转化成增广拉格朗日式[10],为$$ \begin{split} & L({u_k}(t),{f_k},\lambda (t)) = \alpha \sum\limits_{k = 1}^K {\left\| {\frac{d}{{dt}}\left[ {(\delta (t) + \frac{j}{{\pi t}})*{u_k}(t)} \right]{e^{ - j2\pi {f_k}t}}} \right\|} _2^2 +\\& \quad \left\| {y'(t) - \sum\limits_{k = 1}^K {{u_k}(t)} } \right\|_2^2 + \left\langle {\lambda (t),y'(t) - \sum\limits_{k = 1}^K {{u_k}(t)} } \right\rangle \end{split}$$ (3) 式(3)中,共有3项,第1项为模态分解,
$ \delta (t) $ 是狄拉克函数;$ j $ 是希尔伯特旋转因子;*为卷积运算。第1项的运算包含了VMD的3个步骤:第1步的卷积运算为希尔伯特变换,用于分解得出各个IMF;第2步乘以虚指数将IMF倍增,并搬移到中心频率范围;第3步对时间
$ t $ 求偏导数后计算矩阵的2范数的平方,以估计基带带宽。第2项和第3项共同包含一个限制条件,即式(1),
$ \lambda (t) $ 是拉格朗日乘子;$ \alpha $ 是惩罚因子。显然,想要求$ u_k(t),f_k,\lambda(t) $ 的最优解,首先要确定系数$ K $ 和$ \alpha $ 。按照VMD的分解步骤,确定模态分解的深度
$ K $ ,$ K $ 值过小会导致欠分解,影响机车信号解调精度;$ K $ 值过大会导致分解次数过多,过度占用硬件资源,导致系统的实时性差。将分解得到的IMF和原信号进行相关计算,得到Pearson相关系数[11],衡量分解后IMF和原信号之间的关联程度。把Pearson相关系数作为分解深度$ K $ 的评估指标,用于实时调整分解深度$ K $ ,避免欠分解和过分解情况出现。$$ p = \frac{{\displaystyle\sum\limits_{i = 1}^n {({u_i} - \overline u )(y{'_i} - \overline {y'} )} }}{{\sqrt {\displaystyle\sum\limits_{i = 1}^n {{{({u_i} - \overline u )}^2}{{(y{'_i} - \overline {y'} )}^2}} } }} $$ (4) 式(4)中,
$ {u_i} $ 为IMF的机车信号;$ y{'_i} $ 为滤波后的机车信号;$ \overline u $ 为$ {u_i} $ 的平均值;$ \overline {y'} $ 为$ y{'_i} $ 的平均值;Pearson相关系数的取值范围在(−1,1),计算结果数值越大代表相关度越高,p的正负代表的是正相关和负相关类型。基于Pearson相关系数计算VMD参数,设置惩罚因子
$ \alpha $ 为1000 ,对$ y'(t) $ 进行分解并得到$ {u_k}(t) $ 。其次,将$ {u_k}(t) $ 和$ y'(t) $ 离散化为$ {u_i} $ 和$ y{'_i} $ 代入式(4)计算Pearson相关系数,利用$ p({u_k},y') $ 的绝对值判断二者的相关程度:$ 0.8 < \left| p \right| \leqslant 1 $ ,强相关;$ 0.6 < \left| p \right| \leqslant 0.8 $ ,高度相关;$ 0.4 < \left| p \right| \leqslant 0.6 $ ,中度相关;$ 0.2 < \left| p \right| \leqslant 0.4 $ ,弱相关;$ 0 < \left| p \right| \leqslant 0.2 $ ,基本无关。相关系数的绝对值≥0.2代表模态分解没有完成,重复以上分解步骤,直到相关系数小<0.2,记录下此时$ K $ 值,完成参数$ K $ 的优化。$ K $ 值确定好之后,设定$ \alpha $ 取值范围的上下限制$ {\alpha _{\max }} $ 、$ {\alpha _{\min }} $ ,以及$ \alpha $ 的迭代步长$ \mu $ ,代入式(3)计算模态对应的基带带宽,找出最窄基带对应的$ \alpha $ 值,此时系数$ [K,a] $ 即为最优参数。1.3 希尔伯特变换
VMD后,得到的IMF是一组单分量信号,经过希尔伯特变换得到
$$ {\hat u_k}(t) = \frac{1}{\pi }\int_{ - \infty }^{ + \infty } {\frac{{{u_k}(\tau )}}{{t - \tau }}} d\tau = {u_k}(t)*\frac{1}{{\pi t}} $$ (5) 式(5)中,希尔伯特变换的本质是将输入信号和
$ h(t) = \dfrac{1}{{\pi t}} $ 做卷积,从频谱上看,希尔伯特变换是一个带旋转因子的滤波器,不改变原信号的幅值,只改变相位,因此,构建解析式用于谱分析为$$ z(t) = {u_k}(t)+i{\hat u_k}(t) $$ (6) 再由式(7)计算每个IMF的瞬时幅度、相位、角频率,解调机车信号为
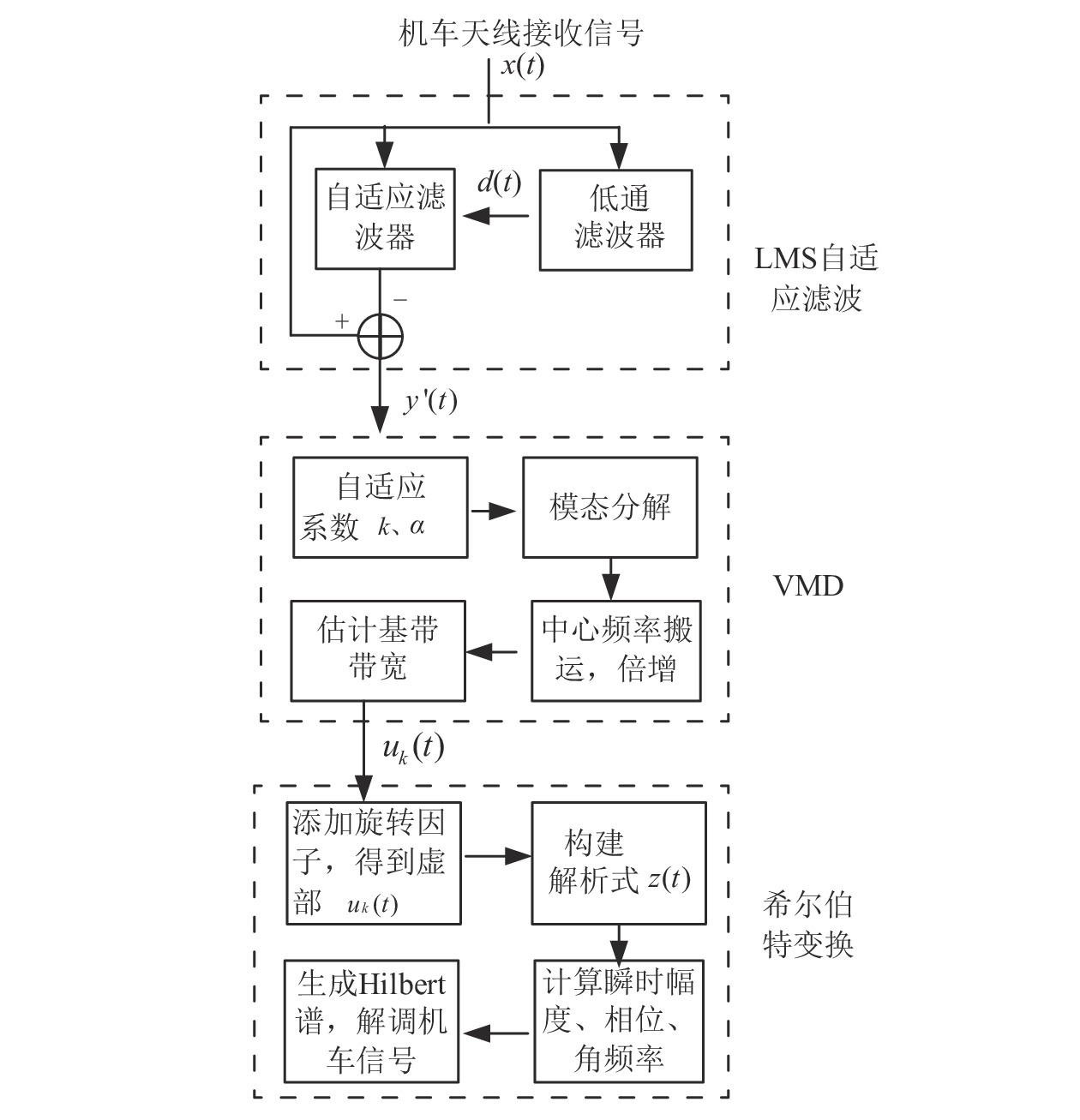
$$ \left\{ \begin{gathered} {\alpha _k}(t) = \sqrt {{u^2}_k(t) + {{\hat u}^2}_k(t)} \\ {\theta _k}(t) = \arctan ({\hat u_k}(t)/{u_k}(t)) \\ {\omega _k}(t) = d{\theta _k}(t)/dt \\ \end{gathered} \right. $$ (7) 基于以上过程,解调的方法总结如图3所示。
2 仿真测试及分析
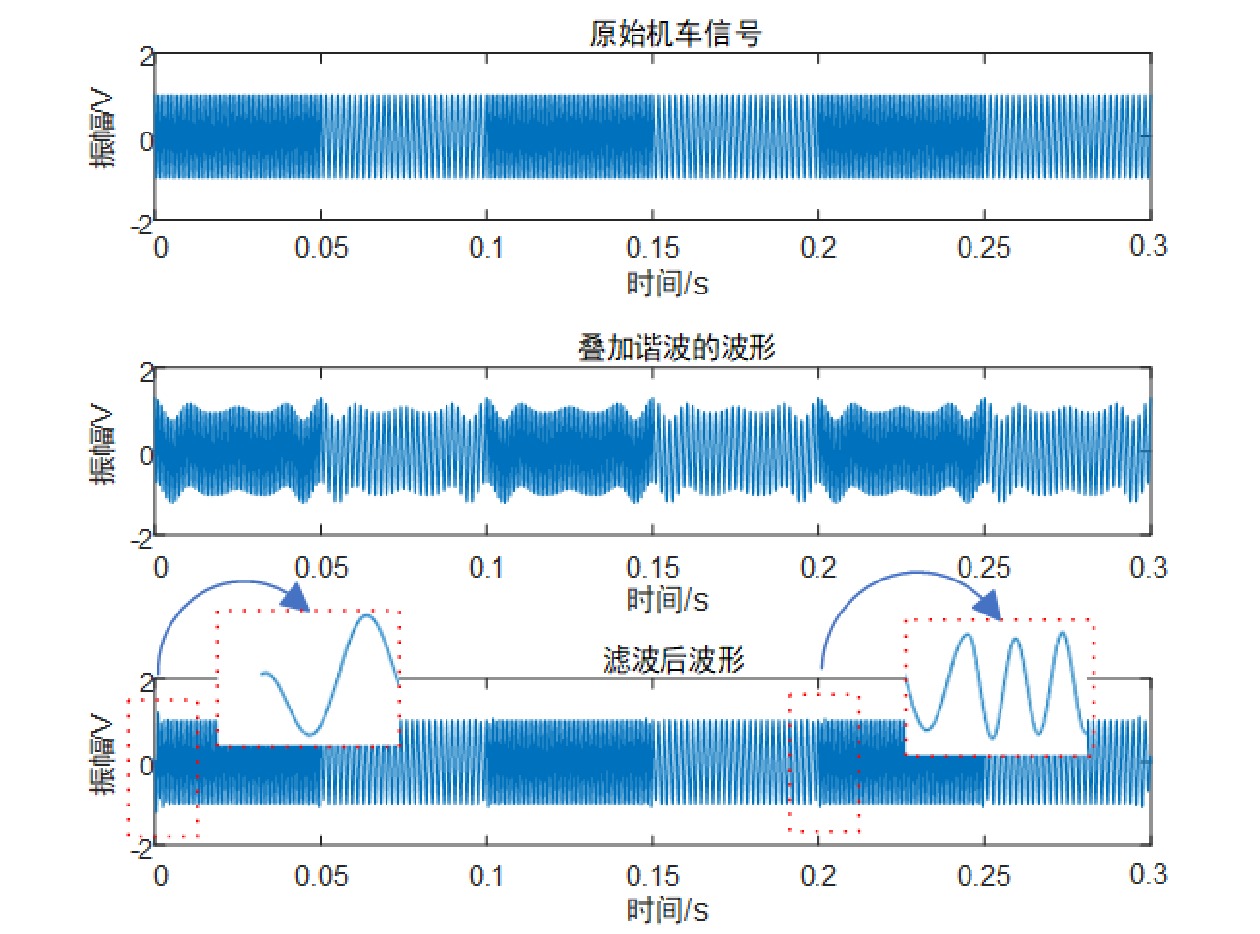
为了验证以上方法的可行性及精度,使用Matlab对其进行验证。设置原始机车信号的中心频率为
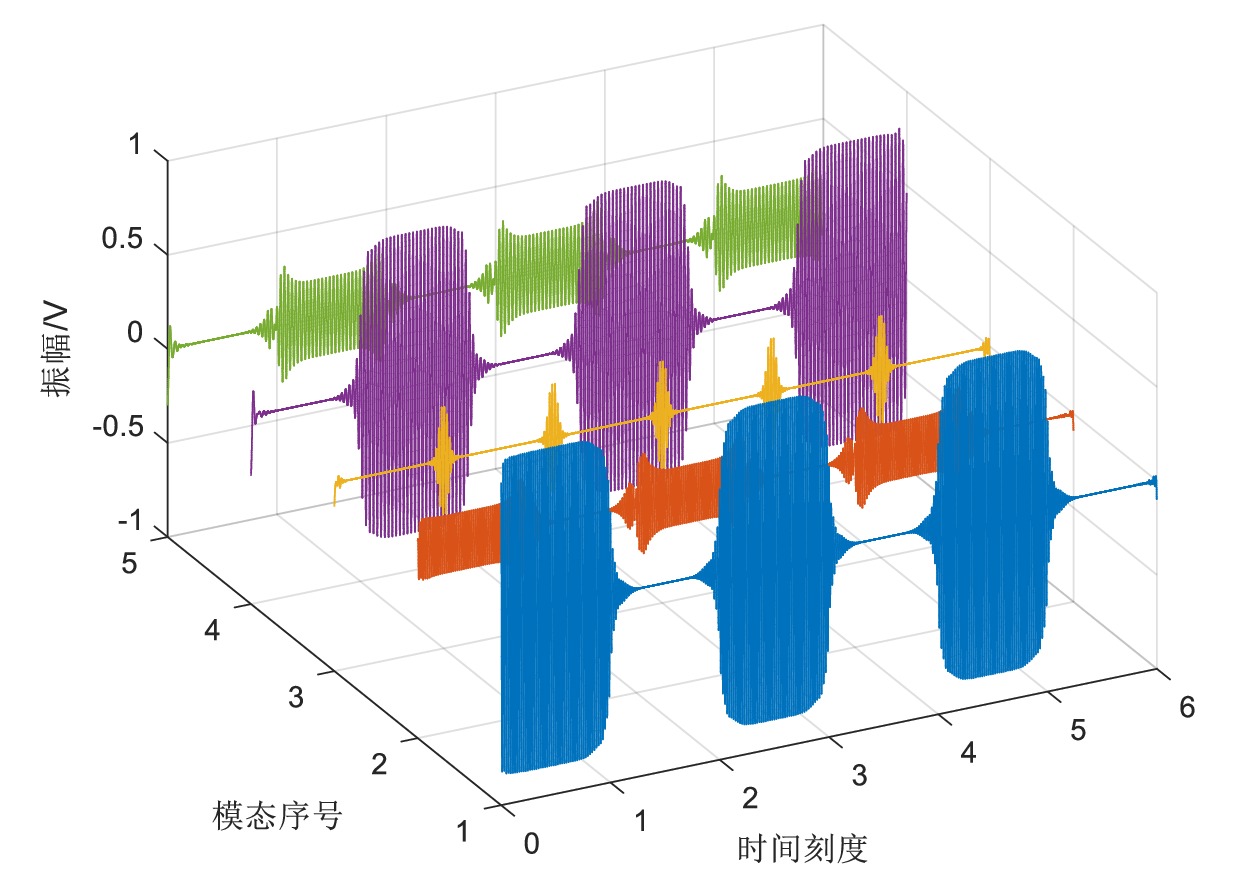
1701.4 Hz,低频调制信号为10.3 Hz,振幅为1 V。根据表1数据,为原始机车信号叠加频率为50 Hz、150 Hz、250 Hz、350 Hz、450 Hz、550 Hz的谐波信号,对应的占比分别为:97.3%、19.88%、9.74%、5.11%、2.76%、1.64%,其余高次谐波,次数越高占比较小,所以忽略。如图4所示,分别列出了原始机车信号、添加谐波的机车信号及经过滤波器处理的信号。LMS自适应滤波器有较好的滤波效果,但在信号的端点处及上下边频交界处略有失真,该失真表现在幅度上的不统一,非相位不连续。对滤波之后的波形进行VMD,分解后的波形如图5所示。x轴代表的是时间刻度,每格约为0.049 s,y轴代表IMF的序号,z轴为振幅。总共分解出5组IMF,信号经过VMD处理后能量和频率被分散到各组IMF,每组IMF只含有单一的瞬时频率。从三维图上可以看出,能量主要集中在IMF1和IMF4,其他模态波形是能量泄露导致的,主要来自于滤波器上/下边频交界处的波形失真。IMF1包含机车信号上边频的主要能量,IMF4包含下边频的主要能量,它们能量的集中分布情况在时间轴上交替间隔出现。图5中IMF1、IMF4两组模态的边界处并没有和时间刻度完全对应,这是LMS自适应滤波器的相位滞后作用所导致的,由滤波器设计工具Filter Design Tool的数据折算可得波形滞后时间约为0.004 85 s,在下一步产生时−频谱时,需要对波形时移进行补偿,修正相位滞后带来的误差。
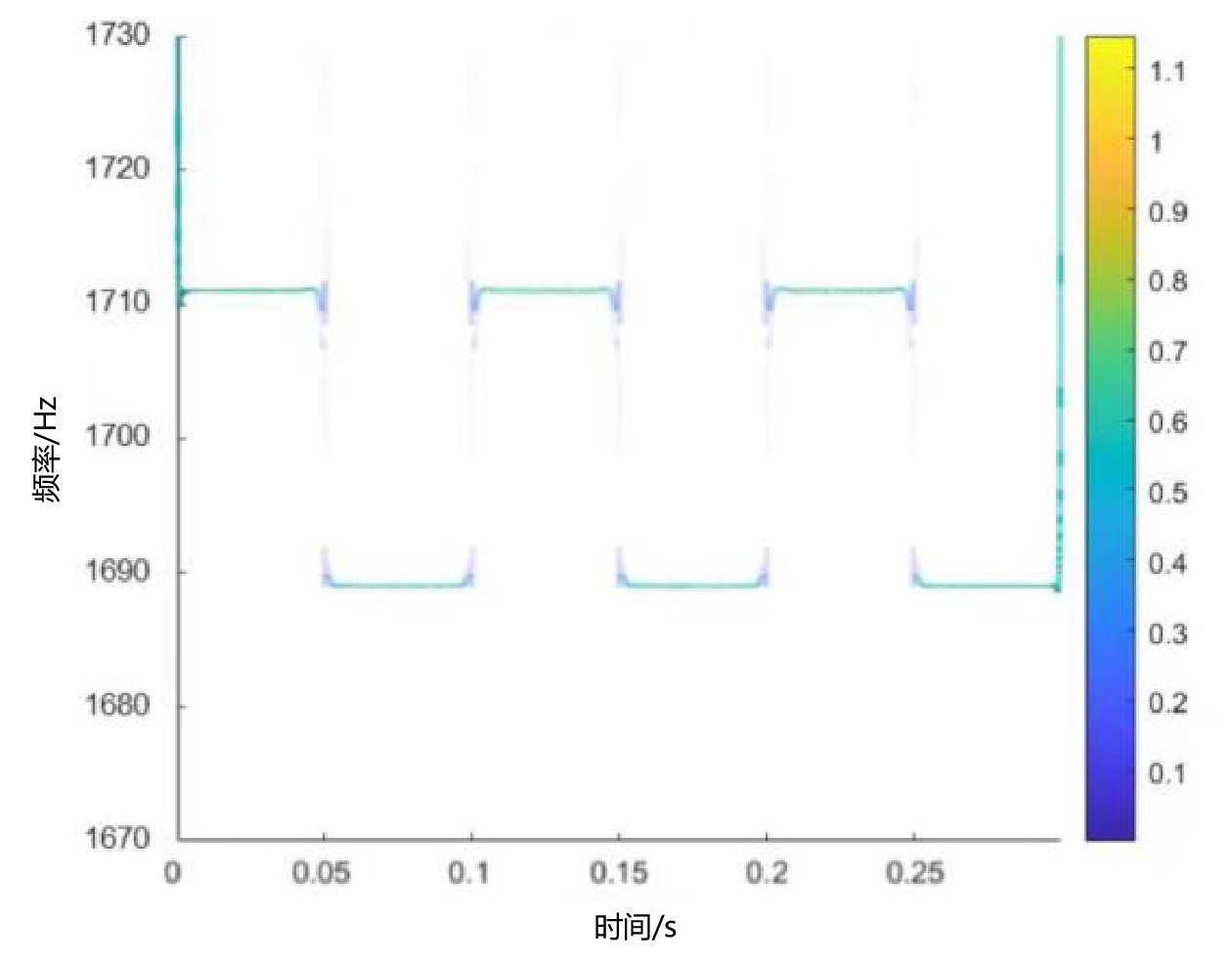
利用式(6)构建解析式,再利用式(7)计算幅度、频率、相位等数据,得到希尔伯特谱如图6所示。横轴为时间、纵轴为频率,谱线的颜色深度代表能量强度。谱图两端有两条向上延伸的谱线,这是机车天线采样信号首尾端点处波形不连续所导致,所以在统计频率数据时,采样周期的起点和末尾附近的数据应直接舍弃。从谱线的颜色看,上下边频颜色偏重,交界处能量泄露谱线颜色偏浅,说明大部分能量集中在机车信号上下边频上,这一现象和图5模态分解能量分布情况相对应。图6很好地描述了机车信号各时间点上的频率及其对应的强度,再对谱数据进行中位值平均滤波[12],即可滤除交界处的干扰,得到准确解调结果。上边频和下边频的频率可直接从谱数据取得,低频信号的周期可从一组上下边频的宽度折算出来。
3 实验测试及分析
3.1 解调电路搭建
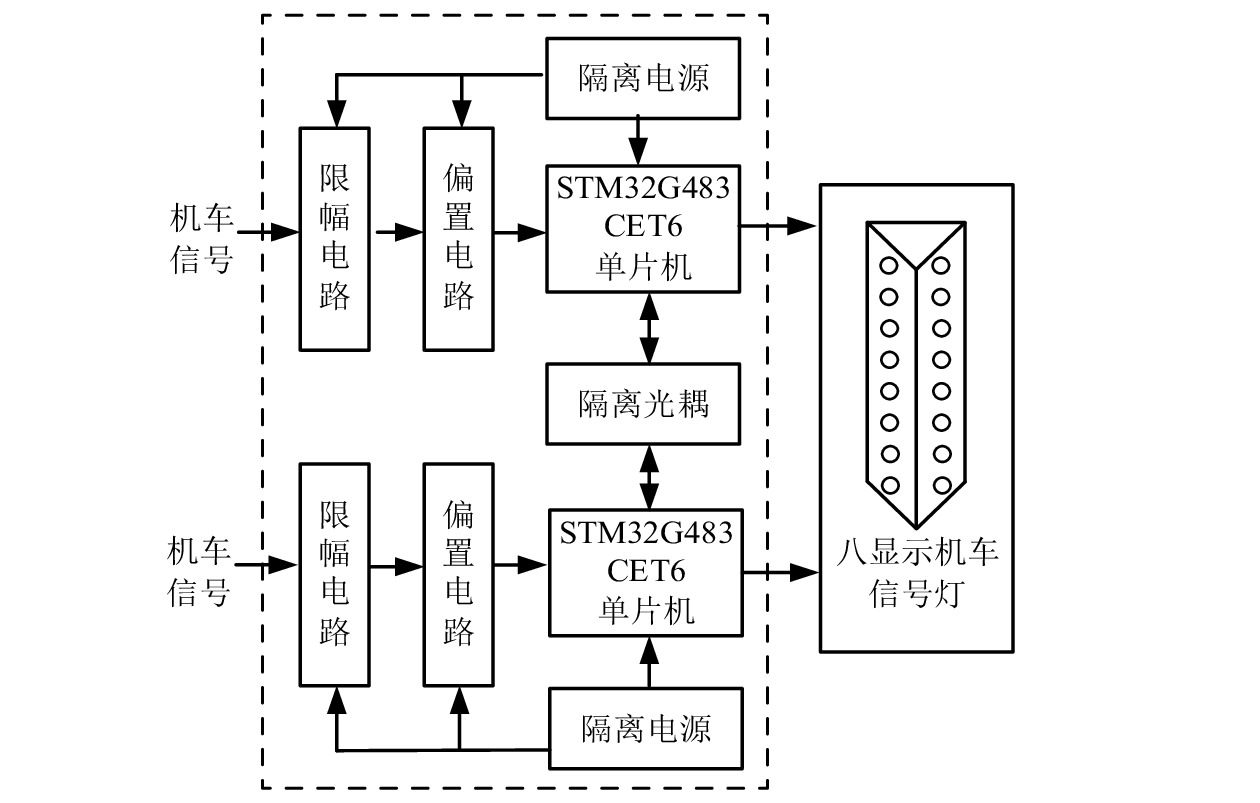
为了测试该方法的实际效果,搭建硬件电路,解调程序的运行平台为32 bit单片机,兼顾单片机功耗及稳定性,选型为STM32G483CET6,该单片机采用的是Cortex-M4内核,有浮点运算单元(FPU, FloatingPoint Unit),能满足解调对小数的计算,官方提供数字信号处理(DSP,Digital Signal Processing)库,可方便编程时直接调用相关的DSP函数。单片机RAM容量为128 kB、FLASH容量为512 kB,运行主频为170 MHz,适合本文方法对机车信号波形的高速采样及大规模数据的存储和变换,解码电路如图7所示。
印制电路板(PCB ,Printed Circuit Board)采用二取二冗余结构设计,每个通道包含各自的单片机及最小系统电路、限幅电路、偏置电路、隔离电源和隔离光耦。限幅电路设置分压电阻,用于按比例缩小输入信号,使用稳压管将采集电压限制在3.3 V以下,并加一级运放隔开信号输入接口和后级电路;偏置电路用于将机车信号调理到单片机AD采样的电压范围,由于单片机只能对正半周采样,偏置电路把信号整体抬高,即可在正半周范围内得到完整波形;两个隔离电源之间是互相隔离的,如果有一路电源故障,不至于影响另外一组通道的电源;单片机的最小系统电路主要包含复位电路和晶振电路,两个单片机的数据交换通过串口实现;使用隔离光耦连接两片单片机的串口。
3.2 信号发生电路搭建
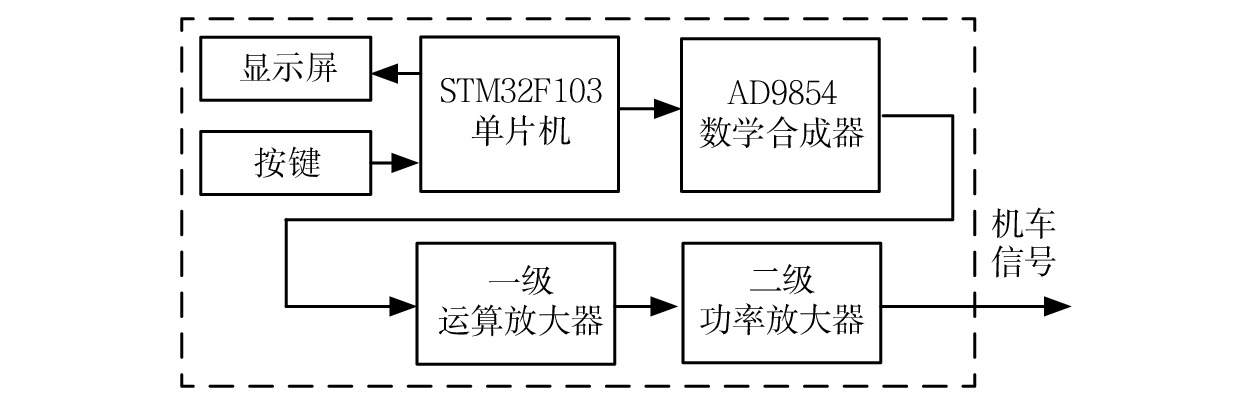
信号发生电路用于合成用于测试的机车信号,方便对解调电路进行测试。为了减小机车信号波形失真对解码精度的影响,选用基于直接数字合成器(DDS,Direct Digital Synthesizer)AD9854设计[13],在Ramped FSK模式下合成机车信号。Ramped FSK模式能够实现频率的渐变,即在FSK信号上/下边频交界处的频率不是突然变化的,而是按照一定斜率缓慢过渡,使波形在交界处光滑,满足正交FSK[14]条件。数字合成器AD9854具有48 bit的频率调谐字,所设置频率的最小步长为1
$ \mu {\text{Hz}} $ ,拥有12 bit数模转换器,以保证其输出波形频率的精确性和光滑程度,信号发生电路结构如图8所示。STM32F103单片机是控制器,用来控制直接数字合成器AD9854组合不同载频及低频调制信号产生期望的机车信号,一级运算放大器使用低失调、低漂移的轨到轨运算放大器OPA333,用于匹配阻抗,二级功率放大器选用D类音频功率放大器TPA3116D2,最大功率可达100 W。键盘和屏幕是人机交互接口,用来设置载频和低频。
3.3 硬件测试与分析
测试实物如图9所示,数字合成器AD9854的PCB和解码电路的PCB插在测试母板上,通过母板上的线路连接,以保证接线的可靠性。测试时,可利用按键和屏幕设置产生固定的机车信号。也可以设置自动扫频模式,单片机控制直接数字合成器AD9854按顺序组合所有载频和所有低频,间隔一定时间输出。利用单片机仿真器可在线查看解调电路的运算数据。
表2和表3的数据是基于ZPW-2000轨道电路的
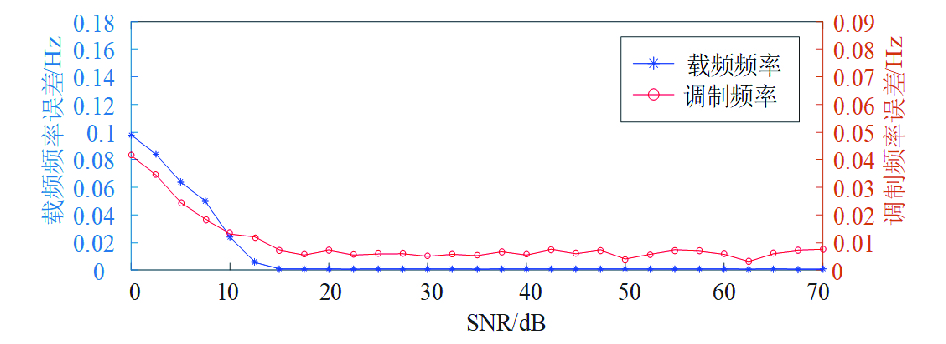
1700 Hz载频,对其1型载频1701.4 Hz和2型载频1698.7 Hz,按照18种低频调制信号进行测试得到的实验数据,可以看出,无论是载频的解调结果还是低频调制信号的解调结果,都具有较高的精度,载频测试误差不超过0.001 Hz,可以明显区分1型载频和2型载频。低频调制信号的测试误差不超过0.01 Hz,远小于低频信号1.1 Hz的频率间隔,不会产生频率混叠问题。表 2 解调结果(1700 -1型载频)单位:Hz 输入信号 解调结果 误差 输入信号 解调结果 误差 调制频率 载频频率 调制频率 载频频率 调制频率 调制频率 载频频率 调制频率 载频频率 调制频率 10.3 1701.3995 10.298 − 0.0005 −0.002 20.2 1701.4001 20.196 + 0.0001 −0.004 11.4 1701.3993 11.402 − 0.0007 +0.002 21.3 1701.4003 21.301 + 0.0003 +0.001 12.5 1701.4002 12.495 + 0.0002 −0.005 22.4 1701.3996 22.399 − 0.0004 −0.001 13.6 1701.4007 13.604 + 0.0007 +0.004 23.5 1701.4000 23.500 0.0000 0.000 14.7 1701.3997 14.696 − 0.0003 −0.004 24.6 1701.4000 24.602 0.0000 +0.002 15.8 1701.3995 15.805 − 0.0005 +0.005 25.7 1701.4002 25.695 + 0.0002 −0.005 16.9 1701.3994 16.903 − 0.0006 +0.003 26.8 1701.3998 26.801 − 0.0002 +0.001 18.0 1701.3999 17.997 − 0.0001 −0.003 27.9 1701.3997 27.901 − 0.0003 +0.001 19.1 1701.4000 19.106 0.0000 +0.006 29.0 1701.4000 29.000 0.0000 0.000 表 3 解调结果(1700 -2型载频)单位:Hz 输入信号 解调结果 误差 输入信号 解调结果 误差 调制频率 载频频率 调制频率 载频频率 调制频率 调制频率 载频频率 调制频率 载频频率 调制频率 10.3 1698.6994 10.299 − 0.0006 −0.001 20.2 1698.7000 20.198 0.0000 −0.002 11.4 1698.7000 11.399 0.0000 −0.001 21.3 1698.7001 21.298 + 0.0001 −0.002 12.5 1698.7001 12.497 + 0.0001 −0.003 22.4 1698.6994 22.405 − 0.0006 +0.005 13.6 1698.6995 13.601 − 0.0005 +0.001 23.5 1698.7000 23.501 0.0000 +0.001 14.7 1698.6992 14.696 − 0.0008 −0.004 24.6 1698.7002 24.600 + 0.0002 0.000 15.8 1698.6999 15.802 − 0.0001 +0.002 25.7 1698.6995 25.694 − 0.0005 −0.006 16.9 1698.7002 16.901 + 0.0002 +0.001 26.8 1698.7000 26.802 0.0000 +0.002 18.0 1698.7003 17.995 + 0.0003 −0.005 27.9 1698.7003 27.900 + 0.0003 0.000 19.1 1698.7000 19.101 0.0000 +0.001 29.0 1698.6999 28.999 − 0.0001 −0.001 利用直接数字合成器AD9854的其余输出通道给机车信号叠加干扰谐波,测试该方法在不同信噪比(SNR,Signal Noise Ratio)下的误差情况。从图10可以看出,在较高的SNR下,解调结果呈现了很高的精度,在较低SNR下(SNR<10 dB),载频和低频调制信号的解调误差分别不超过0.1 Hz和0.05 Hz,不会产生频率混叠问题。
4 结束语
本文介绍了一种基于参数优化VMD和希尔伯特变换的机车信号解调方法,利用LMS自适应滤波器对被采样信号进行滤波,采用VMD对信号进行模态分解,最后利用希尔伯特变换解析出机车信号。得到如下结论:
(1)自适应滤波器克服了经典滤波器只能工作在固定通频带的缺点,能够自动调整滤波系数,可在随机环境中持续地滤除钢轨上的干扰谐波。滤波器实现方法简单,移植到单片机上也可发挥出色的滤波性能,但自适应滤波器的相位滞后作用及上/下边频交界处的失真问题需要在后续步骤里进行处理。
(2)参数优化VMD根据不同载频、不同低频调制信号、不同噪声自动修改参数
$ K $ 和$ \alpha $ ,以获得较好的重构精度。从各个IMF时域图上看,上边频信号和下边频信号被分解到了不同模态,这是机车信号可作谱分析的前提条件。(3)基于希尔伯特变换对IMF做时频分析,利用上/下边频谱线可推算出载频频率;利用谱线的宽度,可推算出低频调制信号的频率。
(4)直接数字合成器AD9854在Ramped FSK模式下产生的正交FSK信号在上/下边频交界处有渐变性,波形相位连续且光滑,抑制了能量泄露问题,在时−频谱图上能量集中,有助于提高机车信号的解调精度。
-
表 1 牵引电流谐波比例
谐波
次数谐波
频率/Hz占百
分比谐波
次数谐波
频率/Hz占百
分比谐波
次数谐波
频率/Hz占百
分比1 50 97.3% 8 400 0.36% 15 750 0.74% 2 100 0.45% 9 450 2.76% 16 800 0.32% 3 150 19.88% 10 500 0.34% 17 850 0.70% 4 200 0.53% 11 550 1.64% 18 900 0.27% 5 250 9.74% 12 600 0.34% 19 950 0.72% 6 300 0.41% 13 650 0.99% 20 1000 0.24% 7 350 5.11% 14 700 0.32% 21 1050 0.63% 表 2 解调结果(
1700 -1型载频)单位:Hz 输入信号 解调结果 误差 输入信号 解调结果 误差 调制频率 载频频率 调制频率 载频频率 调制频率 调制频率 载频频率 调制频率 载频频率 调制频率 10.3 1701.3995 10.298 − 0.0005 −0.002 20.2 1701.4001 20.196 + 0.0001 −0.004 11.4 1701.3993 11.402 − 0.0007 +0.002 21.3 1701.4003 21.301 + 0.0003 +0.001 12.5 1701.4002 12.495 + 0.0002 −0.005 22.4 1701.3996 22.399 − 0.0004 −0.001 13.6 1701.4007 13.604 + 0.0007 +0.004 23.5 1701.4000 23.500 0.0000 0.000 14.7 1701.3997 14.696 − 0.0003 −0.004 24.6 1701.4000 24.602 0.0000 +0.002 15.8 1701.3995 15.805 − 0.0005 +0.005 25.7 1701.4002 25.695 + 0.0002 −0.005 16.9 1701.3994 16.903 − 0.0006 +0.003 26.8 1701.3998 26.801 − 0.0002 +0.001 18.0 1701.3999 17.997 − 0.0001 −0.003 27.9 1701.3997 27.901 − 0.0003 +0.001 19.1 1701.4000 19.106 0.0000 +0.006 29.0 1701.4000 29.000 0.0000 0.000 表 3 解调结果(
1700 -2型载频)单位:Hz 输入信号 解调结果 误差 输入信号 解调结果 误差 调制频率 载频频率 调制频率 载频频率 调制频率 调制频率 载频频率 调制频率 载频频率 调制频率 10.3 1698.6994 10.299 − 0.0006 −0.001 20.2 1698.7000 20.198 0.0000 −0.002 11.4 1698.7000 11.399 0.0000 −0.001 21.3 1698.7001 21.298 + 0.0001 −0.002 12.5 1698.7001 12.497 + 0.0001 −0.003 22.4 1698.6994 22.405 − 0.0006 +0.005 13.6 1698.6995 13.601 − 0.0005 +0.001 23.5 1698.7000 23.501 0.0000 +0.001 14.7 1698.6992 14.696 − 0.0008 −0.004 24.6 1698.7002 24.600 + 0.0002 0.000 15.8 1698.6999 15.802 − 0.0001 +0.002 25.7 1698.6995 25.694 − 0.0005 −0.006 16.9 1698.7002 16.901 + 0.0002 +0.001 26.8 1698.7000 26.802 0.0000 +0.002 18.0 1698.7003 17.995 + 0.0003 −0.005 27.9 1698.7003 27.900 + 0.0003 0.000 19.1 1698.7000 19.101 0.0000 +0.001 29.0 1698.6999 28.999 − 0.0001 −0.001 -
[1] 李 辉,何之煜,颉洪睿. 基于希尔伯特黄变换的机车信号解调算法研究[J]. 计算机仿真,2023,40(8):136-140. DOI: 10.3969/j.issn.1006-9348.2023.08.025 [2] LIU C, YANG S W, CUI Y, et al. Quantitative analysis on coupling of traction current into cab signaling in electrified railways[J]. Railway Engineering Science, 2020, 28(3): 275-289. DOI: 10.1007/s40534-020-00220-z
[3] 孔德龙. 自适应滤波算法在轨道电路FSK信号解调中的应用与研究[D]. 兰州:兰州交通大学,2014. [4] 马罗文,刘 宁,胡心语,等. FFT幅相联合的快速高精度频率估计方法[J]. 计测技术,2022,42(6):34-39. [5] 李昊宇,黄丹平,罗 凡. 非整周期低信噪比科氏流量计相位差测量研究[J]. 国外电子测量技术,2023,42(11):89-96. [6] 朱崇巧. 基于HHT的高速铁路钢轨波磨检测方法[J]. 电子测量技术,2018,41(6):19-26. [7] 佘嘉演,朱维斌,黄 垚,等. 基于希尔伯特-黄变换的转台角速率测量方法研究[J]. 仪表技术与传感器,2024,(4):107-111. DOI: 10.3969/j.issn.1002-1841.2024.04.019 [8] 李德权. 电气化铁路谐波测试及治理技术[J]. 电气化铁道,2023,34(S2):123-126. [9] 李斌斌,寇西平,吕彬彬,等. 基于自适应LMS算法的跨声速风洞模型系统辨识[J]. 振动与冲击,2024,43(3):164-170. [10] 张海强,王 楠,刘 松,等. 基于参数优化VMD和SPWVD的轨道波磨辨识方法[J]. 铁路计算机应用,2020,29(6):18-24. [11] 朱少民,夏 虹,尹文哲,等. 基于变分模态分解和希尔伯特变换的转子非平稳信号故障特征识别[J]. 哈尔滨工程大学学报,2024,45(5):825-832. DOI: 10.11990/jheu.202205050 [12] 张宏谋,李竹君,徐文强,等. 温度测量系统中可调参数中位值平均滤波低复杂度算法[J]. 电子设计工程,2020,28(1):168-171. [13] 杨 城,刁艳美. 移频轨道电路发码装置的研究与设计[J]. 铁路计算机应用,2023,32(9):72-77. DOI: 10.3969/j.issn.1005-8451.2023.09.13 [14] 杨 进,杨 城. 基于DDS Ramped FSK技术的机车信号测试系统设计[J]. 电子器件,2015,38(4):831-834. DOI: 10.3969/j.issn.1005-9490.2015.04.023




 下载:
下载: